Skip to main content
Advances in Continuous and Discrete Models

Theory and Modern Applications

Download PDF
  • Research Article
  • Open access
  • Published:

Results and Conjectures about Order 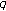Lyness' Difference Equatio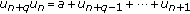n in 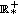, with a Particular Study of the Case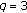

Advances in Difference Equations volume 2009, Article number: 134749 (2009) Cite this article

Abstract

We study order Lyness' difference equation in , with and the associated dynamical system in . We study its solutions (divergence, permanency, local stability of the equilibrium). We prove some results, about the first three invariant functions and the topological nature of the corresponding invariant sets, about the differential at the equilibrium, about the role of 2-periodic points when is odd, about the nonexistence of some minimal periods, and so forth and discuss some problems, related to the search of common period to all solutions, or to the second and third invariants. We look at the case with new methods using new invariants for the map and state some conjectures on the associated dynamical system in in more general cases.

Publisher note

To access the full article, please see PDF

Author information

Authors and Affiliations

  1. Institut de Mathématiques de Jussieu, UPMC-Paris 06, UMR-CNRS 7586, 75251, Paris, France

    G. Bastien

  2. Laboratoire Paul Painlevé, USTL Lille 1, UMR-CNRS 8524, 59655, Villeneuve, France

    M. Rogalski

  3. Equipe d'Analyse fonctionnelle, IMJ, 16 rue Clisson, 75013, Paris, France

    G. Bastien & M. Rogalski

Authors
  1. G. Bastien
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Rogalski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Bastien.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article

Bastien, G., Rogalski, M. Results and Conjectures about Order 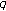Lyness' Difference Equatio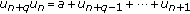n in 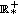, with a Particular Study of the Case 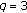. Adv Differ Equ 2009, 134749 (2009). https://doi.org/10.1155/2009/134749

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/2009/134749

Keywords