- Research Article
- Open access
- Published:
Uniform Asymptotic Stability and Robust Stability for Positive Linear Volterra Difference Equations in Banach Lattices
Advances in Difference Equations volume 2008, Article number: 598964 (2008)
Abstract
For positive linear Volterra difference equations in Banach lattices, the uniform asymptotic stability of the zero solution is studied in connection with the summability of the fundamental solution and the invertibility of the characteristic operator associated with the equations. Moreover, the robust stability is discussed and some stability radii are given explicitly.
1. Introduction
A dynamical system is called positive if any solution of the system starting from nonnegative states maintains nonnegative states forever. In many applications where variables represent nonnegative quantities we often encounter positive dynamical systems as mathematical models (see [1, 2]), and many researches for positive systems have been done actively; for recent developments see, for example, [3] and the references therein.
In this paper we treat the Volterra difference equations

together with

in a (complex) Banach lattice X, where  is a sequence of compact linear operators on
is a sequence of compact linear operators on  satisfying the summability condition
satisfying the summability condition  , and we study stability properties of (1.1) and (1.2) under the restriction that the operators
, and we study stability properties of (1.1) and (1.2) under the restriction that the operators  , are positive. In fact, the restriction on
, are positive. In fact, the restriction on  yields the positivity for the above equations (whose notion is introduced in Section 2). Also, without the restriction, in [4] the authors characterized the uniform asymptotic stability of the zero solution of (1.1), together with (1.2), in connection with the invertibility of the characteristic operator
yields the positivity for the above equations (whose notion is introduced in Section 2). Also, without the restriction, in [4] the authors characterized the uniform asymptotic stability of the zero solution of (1.1), together with (1.2), in connection with the invertibility of the characteristic operator

of (1.1) for any complex numbers  such that
such that  . In Section 3, we will prove that under the restriction that the operators
. In Section 3, we will prove that under the restriction that the operators  , are positive, the invertibility of the characteristic operator reduces to that of the operator
, are positive, the invertibility of the characteristic operator reduces to that of the operator  , and consequently the uniform asymptotic stability of the zero solution for positive equations is equivalent to the condition which is much easier than the one for the characteristic operator in checking (Theorem 3.6). Moreover, we will discuss in Section 4 the robust stability of (1.1) and give explicit formulae of some stability radii.
, and consequently the uniform asymptotic stability of the zero solution for positive equations is equivalent to the condition which is much easier than the one for the characteristic operator in checking (Theorem 3.6). Moreover, we will discuss in Section 4 the robust stability of (1.1) and give explicit formulae of some stability radii.
2. Preliminaries
Let  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  be the sets of natural numbers, nonnegative integers, nonpositive integers, integers, nonnegative real numbers, real numbers and complex numbers, respectively.
be the sets of natural numbers, nonnegative integers, nonpositive integers, integers, nonnegative real numbers, real numbers and complex numbers, respectively.
To make the presentation self-contained, we give some basic facts on Banach lattices which will be used in the sequel (see, e.g., [5]). Let  be a real vector space endowed with an order relation
be a real vector space endowed with an order relation  Then
Then  is called an ordered vector space. Denote the positive elements of
is called an ordered vector space. Denote the positive elements of  by
by  . If furthermore the lattice property holds, that is, if
. If furthermore the lattice property holds, that is, if  for
for  then
then  is called a vector lattice. It is important to note that
is called a vector lattice. It is important to note that  is generating, that is,
is generating, that is,

Then, the modulus of  is defined by
is defined by  If
If  is a norm on the vector lattice
is a norm on the vector lattice  satisfying the lattice norm property, that is, if
satisfying the lattice norm property, that is, if

then  is called a normed vector lattice. If, in addition,
is called a normed vector lattice. If, in addition,  is a Banach space, then
is a Banach space, then  is called a (real) Banach lattice.
is called a (real) Banach lattice.
We now extend the notion of Banach lattices to the complex case. For this extension all underlying vector lattices  are assumed to be relatively uniformly complete, that is, if for every sequence
are assumed to be relatively uniformly complete, that is, if for every sequence  in
in  satisfying
satisfying  and for every
and for every  and every sequence
and every sequence  in
in  , it holds that
, it holds that

Now, let  be a relatively uniformly complete vector lattice. The complexification of
be a relatively uniformly complete vector lattice. The complexification of  is defined by
is defined by  The modulus of
The modulus of  is defined by
is defined by

A complex vector lattice is defined as the complexification of a relatively uniformly complete vector lattice equipped with the modulus (2.4). If  is normed, then
is normed, then

defines a norm on  satisfying the lattice norm property; in fact, the norm restricted to
satisfying the lattice norm property; in fact, the norm restricted to  is equivalent to the original norm in
is equivalent to the original norm in  , and we use the same symbol
, and we use the same symbol  to denote the (new) norm. If
to denote the (new) norm. If  is a Banach lattice, then
is a Banach lattice, then  equipped with the modulus (2.4) and the norm (2.5) is called a complex Banach lattice, and
equipped with the modulus (2.4) and the norm (2.5) is called a complex Banach lattice, and  is called the real part of
is called the real part of  .
.
For Banach spaces  and
and  , we denote by
, we denote by  the Banach space of all bounded linear operators from
the Banach space of all bounded linear operators from  to
to  equipped with the operator norm, and use the notation
equipped with the operator norm, and use the notation  in place of
in place of  . Let
. Let  and
and  be Banach lattices with real parts
be Banach lattices with real parts  and
and  , respectively. An operator
, respectively. An operator  is called real if
is called real if  . A linear operator
. A linear operator  from
from  to
to  is called positive, denoted by
is called positive, denoted by  , if
, if  holds. Such an operator is necessarily bounded (see [5]) and hence real. Denote by
holds. Such an operator is necessarily bounded (see [5]) and hence real. Denote by  and
and  the sets of real operators and positive operators between
the sets of real operators and positive operators between  and
and  , respectively:
, respectively:

Then we observe that

Indeed, it is clear that the inequality holds true for any  , the real part of
, the real part of  . Let
. Let  with
with  and
and  . Since
. Since  by (2.4), we get
by (2.4), we get

with  and
and  . Then, it follows from the modulus (2.4) that
. Then, it follows from the modulus (2.4) that

as required. We also emphasize the simple fact that

(see, e.g., [5, page 230]). Moreover, by the symbol  we mean
we mean  for
for  Throughout this paper,
Throughout this paper,  is assumed to be a complex Banach lattice with the real part
is assumed to be a complex Banach lattice with the real part  and the positive convex cone
and the positive convex cone  .
.
For any interval  we use the same notation
we use the same notation  meaning the discrete one
meaning the discrete one  , for example,
, for example,  for
for  . Also, for an
. Also, for an  -valued function
-valued function  on a discrete interval
on a discrete interval  , its norm is denoted by
, its norm is denoted by  . Let
. Let  and a function
and a function  be given. We denote by
be given. We denote by  the solution
the solution  of (1.1) satisfying
of (1.1) satisfying  on
on  . Similarly, for
. Similarly, for  and a function
and a function  , we denote by
, we denote by  the solution
the solution  of (1.2) satisfying
of (1.2) satisfying  on
on  . We then recall the representation formulae of solutions for initial value problems of (1.1) and (1.2) (see [6–8]). Let
. We then recall the representation formulae of solutions for initial value problems of (1.1) and (1.2) (see [6–8]). Let  be the fundamental solution of (1.1) (or (1.2)), that is, the sequence in
be the fundamental solution of (1.1) (or (1.2)), that is, the sequence in  satisfying
satisfying

for  Then, the solution
Then, the solution  is given by
is given by

for arbitrary initial function  , and also for arbitrary initial function
, and also for arbitrary initial function  , the solution
, the solution  of (1.2) is given by
of (1.2) is given by

for  , where we promise
, where we promise  for
for  .
.
Here, we give the definition of the positivity of Volterra difference equations.
Definition 2.1.
Equation (1.1) is said to be positive if for any  and
and  , the solution
, the solution  for
for  . Similarly,(1.2) is said to be positive if for any
. Similarly,(1.2) is said to be positive if for any  and
and  , the solution
, the solution  for
for  .
.
Also, we follow the standard definitions for stabilities of the zero solution.
Definition 2.2.
The zero solution of (1.1) is said to be
-
(i)
uniformly stable if for any
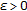 there exists a
there exists a 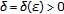 such that if
such that if  and
and  is an initial function on
is an initial function on 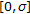 with
with  then
then 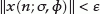 for all
for all  ;
; -
(ii)
uniformly asymptotically stable if it is uniformly stable, and if there exists a
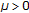 such that, for any
such that, for any 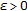 there exists an
there exists an 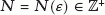 with the property that, if
with the property that, if 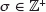 and
and  is an initial function on
is an initial function on 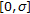 with
with 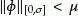 then
then 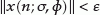 for all
for all  .
.
Definition 2.3.
The zero solution of (1.2) is said to be
-
(i)
uniformly stable if for any
 there exists a
there exists a 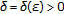 such that if
such that if  and
and 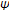 is an initial function on
is an initial function on 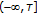 with
with  then
then  for all
for all 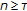 ;
; -
(ii)
uniformly asymptotically stable if it is uniformly stable, and if there exists a
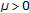 such that, for any
such that, for any  there exists an
there exists an 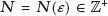 with the property that, if
with the property that, if 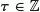 and
and 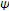 is an initial function on
is an initial function on 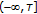 with
with  then
then 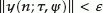 for all
for all 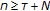 .
.
Here and subsequently,  denotes the Z-transform of
denotes the Z-transform of  ; that is,
; that is,  , which is defined for
, which is defined for  under our assumption
under our assumption  . Then,
. Then,  is called the characteristic operator associated with (1.1) (or (1.2)). In [6, 7], under some restrictive conditions on
is called the characteristic operator associated with (1.1) (or (1.2)). In [6, 7], under some restrictive conditions on  , we discussed the uniform asymptotic stability of the zero solution of (1.2) in connection with the summability of the fundamental solution
, we discussed the uniform asymptotic stability of the zero solution of (1.2) in connection with the summability of the fundamental solution  , as well as the invertibility of the characteristic operator
, as well as the invertibility of the characteristic operator  ; see also [9–12] for the case that
; see also [9–12] for the case that  is finite dimensional. Moreover, we have shown in [4] the equivalence among these three properties without such restrictive conditions; more precisely, we have established the following.
is finite dimensional. Moreover, we have shown in [4] the equivalence among these three properties without such restrictive conditions; more precisely, we have established the following.
Theorem 2.4 (see [4, Theorem 1]).
Let  , and assume that
, and assume that 
 are all compact. Then the following statements are equivalent.
are all compact. Then the following statements are equivalent.
-
(i)
The zero solution of (1.1) is uniformly asymptotically stable.
-
(ii)
The zero solution of (1.2) is uniformly asymptotically stable.
-
(iii)
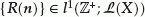 .
. -
(iv)
For any
 such that
such that  , the operator
, the operator 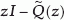 is invertible in
is invertible in 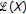 .
.
3. Stability for Positive Volterra Difference Equations
In this section, we will prove that the uniform asymptotic stability of the zero solution of positive Volterra difference equations (1.1) and (1.2) is, in fact, characterized by the invertibility of the operator  for
for  . To this end we need some observations on the spectral radius of the
. To this end we need some observations on the spectral radius of the  -transform of the convolution kernel
-transform of the convolution kernel  .
.
First of all, we show the relation between the positivity of Volterra difference equations and that of the sequence of bounded linear operators  .
.
Proposition 3.1.
Equation (1.1) is positive if and only if all 
 are positive.
are positive.
Proof.
Suppose that all  are positive. Then from (2.11) each element
are positive. Then from (2.11) each element  (
( of the fundamental solution is also positive; so that by virtue of (2.12),
of the fundamental solution is also positive; so that by virtue of (2.12),  for
for  , where
, where  and
and  are arbitrary. Hence, (1.1) is positive. Conversely, suppose (1.1) to be positive. Then we have in particular
are arbitrary. Hence, (1.1) is positive. Conversely, suppose (1.1) to be positive. Then we have in particular  for
for  , which implies that
, which implies that  . Let
. Let  and for
and for  ,
,  be any function such that
be any function such that  except
except  . Then it follows from (2.12) that
. Then it follows from (2.12) that

which implies that  for
for  . Thus,
. Thus,  for
for  since
since  is arbitrary.
is arbitrary.
By using (2.13) one can verify the following proposition quite similarly.
Proposition 3.2.
Equation (1.2) is positive if and only if all 
 are positive.
are positive.
In what follows, we assume that  and each
and each  is compact. For any closed operator
is compact. For any closed operator  on
on  we denote by
we denote by  ,
,  , and
, and  the spectrum, the point spectrum, and the resolvent set of
the spectrum, the point spectrum, and the resolvent set of  , respectively. Also denote by
, respectively. Also denote by  the interior of the unit disk
the interior of the unit disk  of the complex plane. Then for the uniform asymptotic stability of the zero solution of (1.1) we have the following criterion.
of the complex plane. Then for the uniform asymptotic stability of the zero solution of (1.1) we have the following criterion.
Theorem 3.3.
Suppose that (1.1) is positive. If  , the zero solution of (1.1) is uniformly asymptotically stable.
, the zero solution of (1.1) is uniformly asymptotically stable.
Proof.
In view of Theorem 2.4 it is sufficient to show that  is invertible for
is invertible for  with
with  . Suppose by contradiction that
. Suppose by contradiction that  is not invertible for some
is not invertible for some  with
with  . Then
. Then  and hence
and hence  since
since  and
and  is compact. Let
is compact. Let  ,
,  be an eigenvector of the operator
be an eigenvector of the operator  for the eigenvalue
for the eigenvalue  . Then,
. Then,  . We generally get
. We generally get  for any
for any  . Notice that the spectral radius of
. Notice that the spectral radius of  is less than
is less than  by the assumption. Therefore, it follows from the well known Gelfand's formula (see, e.g., [13, Theorem 10.13]) for the spectral radius of bounded linear operators that
by the assumption. Therefore, it follows from the well known Gelfand's formula (see, e.g., [13, Theorem 10.13]) for the spectral radius of bounded linear operators that  , which implies
, which implies  . On the other hand, since
. On the other hand, since  ,
,  are positive by Proposition 3.1, we get
are positive by Proposition 3.1, we get

by (2.7); and generally,

for any  . Therefore,
. Therefore,

and it follows from the lattice norm property that

This is a contradiction, because we must get  by (3.5).
by (3.5).
The converse of Theorem 3.3 also holds. To see this we need another proposition. Let  be the spectral radius of
be the spectral radius of  for
for  .
.
Proposition 3.4.
Suppose that 
 are all positive. Then,
are all positive. Then,  is nonincreasing and continuous as a function on
is nonincreasing and continuous as a function on 
Proof.
Let  . Then,
. Then,

Observe that the resolvent  of
of  (
( is given by
is given by  whenever
whenever  . Then, we deduce from (3.6) that
. Then, we deduce from (3.6) that

Note also that under our assumption  is a positive operator for
is a positive operator for  since
since  is closed in
is closed in  . In particular,
. In particular,  is also positive and hence for
is also positive and hence for  ,
,

by (2.7). Therefore  so that
so that

Now, let us assume that  holds for some
holds for some  and
and  with
with  . Since
. Since  is positive, it follows from [5, Chapter 5, Proposition 4.1] that
is positive, it follows from [5, Chapter 5, Proposition 4.1] that  . Observe that if
. Observe that if  and
and  , then
, then  is invertible in
is invertible in  with
with  . Since
. Since  , the above observation leads to the fact that
, the above observation leads to the fact that  as
as  ; consequently, we get
; consequently, we get  as
as  . On the other hand it follows from
. On the other hand it follows from  for
for  that
that  and the function
and the function  is continuous on
is continuous on  . Hence, we get
. Hence, we get  , which is a contradiction. Consequently,
, which is a contradiction. Consequently,  for
for  .
.
We next show the left continuity of  on
on  . If
. If  is not left continuous at some
is not left continuous at some  , we have
, we have

Since  , we have
, we have  . Notice that
. Notice that  is an open set. Hence, it follows that if
is an open set. Hence, it follows that if  is small enough,
is small enough,  that is,
that is,  for such an
for such an  . On the other hand, by virtue of [5, Chapter 5, Proposition 4.1] again, the positivity of
. On the other hand, by virtue of [5, Chapter 5, Proposition 4.1] again, the positivity of  yields
yields  ; this is a contradiction.
; this is a contradiction.
 is right continuous as well in
is right continuous as well in  . Indeed, if it is not so, there exists a
. Indeed, if it is not so, there exists a  such that
such that

In view of the positivity of  we have
we have  . Also, since
. Also, since  is compact,
is compact,  is an isolated point of its spectrum
is an isolated point of its spectrum  ; in particular, there exists an
; in particular, there exists an  such that
such that  . By the continuity of
. By the continuity of  there corresponds an
there corresponds an  such that
such that  is invertible in
is invertible in  for
for  . Moreover, by the fact that
. Moreover, by the fact that  for
for  , one can see
, one can see

from which  readily follows because of the positivity of
readily follows because of the positivity of  . Therefore, passing to the limit
. Therefore, passing to the limit  , we deduce that
, we deduce that  . Let
. Let  be any number such that
be any number such that  . By the same reasoning, we see that
. By the same reasoning, we see that  . Since
. Since

we get

Then, for  , it follows from (2.7) that
, it follows from (2.7) that

hence

for any  with
with  . This is a contradiction, because
. This is a contradiction, because  as
as  . The proof is now completed.
. The proof is now completed.
Theorem 3.5.
Suppose that (1.1) is positive. If the zero solution of (1.1) is uniformly asymptotically stable, then  .
.
Proof.
Set  . To prove the theorem it is sufficient to show
. To prove the theorem it is sufficient to show  . Assume that
. Assume that  . Since by Proposition 3.4
. Since by Proposition 3.4  is continuous, there exists
is continuous, there exists  such that
such that  , that is,
, that is,  . It follows from the positivity of
. It follows from the positivity of  , together with its compactness, that
, together with its compactness, that  belongs to
belongs to  ; hence, there exists an
; hence, there exists an  such that
such that  , or equivalently
, or equivalently

Setting  , we have
, we have

so that  is a solution of (1.2). By virtue of Theorem 2.4 and our assumption, (1.2) is uniformly asymptotically stable and therefore
is a solution of (1.2). By virtue of Theorem 2.4 and our assumption, (1.2) is uniformly asymptotically stable and therefore  as
as  , which is impossible because
, which is impossible because  for all
for all  . Thus we must have
. Thus we must have  .
.
Combining the results above with Theorem 2.4, we have, for positive Volterra difference equations, the equivalence among the uniform asymptotic stability of the zero solution of (1.1) and (1.2), the summability of the fundamental solution and the invertibility of the operator  outside the unit disk.
outside the unit disk.
Theorem 3.6.
Let the assumptions in Theorem 2.4 hold. If, in addition,  ac.
ac.
-
(i)
The zero solution of (1.1) is uniformly asymptotically stable.
-
(ii)
The zero solution of (1.2) is uniformly asymptotically stable.
-
(iii)
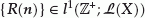
-
(iv)
The operator
 is invertible in
is invertible in 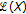 for
for 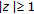 .
.
Before concluding this section, we will give an example to which our Theorem 3.6 is applicable. In [6, 7], following the idea in [14], we have shown that Volterra difference equations on a Banach space  are naturally derived from abstract differential equations on
are naturally derived from abstract differential equations on  with piecewise continuous delays of type
with piecewise continuous delays of type

where  denotes the Gaussian symbol and
denotes the Gaussian symbol and  is the inifinitesimal generator of a strongly continuous semigroup
is the inifinitesimal generator of a strongly continuous semigroup  , of bounded linear operators on
, of bounded linear operators on  , and
, and  ,
,  are bounded linear operators on
are bounded linear operators on  such that
such that

Recall that a function  with
with  is called a (mild) solution of (3.19) on
is called a (mild) solution of (3.19) on  , if
, if  is continuous on
is continuous on  , and satisfies the relation
, and satisfies the relation

In case of  for some
for some  , the relation above yields that
, the relation above yields that

Letting  , we get the Volterra difference equation
, we get the Volterra difference equation

where  are bounded linear operators on
are bounded linear operators on  defined by
defined by

for  Conversely, if
Conversely, if  satisfies (3.23) with
satisfies (3.23) with  , then the function
, then the function  extended to nonintegers
extended to nonintegers  by the relation
by the relation

is a (mild) solution of (3.19). Thus, abstract differential equations of type (3.19) lead to Volterra difference equations on  .
.
Now suppose that the semigroup  is compact. Then,
is compact. Then,  is continuous in
is continuous in  with respect to the operator norm ([15]) and also
with respect to the operator norm ([15]) and also  , defined by the relation (3.24) are compact operators on
, defined by the relation (3.24) are compact operators on  (see [6, Proposition 1]). Moreover, it follows from (3.20) that
(see [6, Proposition 1]). Moreover, it follows from (3.20) that  . Moreover in the restricted case where
. Moreover in the restricted case where  , are given by
, are given by  for some
for some  with
with  , we know by [7, Proposition 1] that the spectrum of the characteristic operator
, we know by [7, Proposition 1] that the spectrum of the characteristic operator  of (3.23) is given by the formula:
of (3.23) is given by the formula:

Hence, in the restricted case, Theorem 2.4 implies that the zero solution of (3.23) is uniformly asymptotically stable if and only if

for all  and
and  .
.
We further assume that  is a complex Banach lattice, the compact semigroup
is a complex Banach lattice, the compact semigroup  on
on  is positive, and that
is positive, and that  are all nonnegative. Then the sequence
are all nonnegative. Then the sequence  defined by (3.24) meets the assumptions in Theorem 3.6. Noticing that
defined by (3.24) meets the assumptions in Theorem 3.6. Noticing that  , we know by Theorem 3.6 in the further restricted case that the zero solution of (3.23) is uniformly asymptotically stable if and only if
, we know by Theorem 3.6 in the further restricted case that the zero solution of (3.23) is uniformly asymptotically stable if and only if

for all  .
.
4. Robust Stability and Some Stability Radii of Positive Volterra Difference Equations
Let (1.1) be uniformly asymptotically stable, that is, the zero solution of (1.1) is uniformly asymptotically stable, and consider a perturbed difference equation of the form

where  are given operators corresponding to the structure of perturbations and
are given operators corresponding to the structure of perturbations and  is an unknown (disturbance) parameter. Here
is an unknown (disturbance) parameter. Here  and
and  are also assumed to be complex Banach lattices. Our objective in this section is to determine various stability radii of (1.1) provided that
are also assumed to be complex Banach lattices. Our objective in this section is to determine various stability radii of (1.1) provided that  are all positive; for this topic in case that the space
are all positive; for this topic in case that the space  is finite dimensional, see, for example, [16] and the references therein. By the stability radius of (1.1) we mean the supremum of positive numbers
is finite dimensional, see, for example, [16] and the references therein. By the stability radius of (1.1) we mean the supremum of positive numbers  such that the uniform asymptotic stability of the perturbed (4.1) persists whenever the size of the perturbation
such that the uniform asymptotic stability of the perturbed (4.1) persists whenever the size of the perturbation  , measured by the
, measured by the  -norm
-norm  , is less than
, is less than  (for precise definitions see the paragraph preceding Theorem 4.3).
(for precise definitions see the paragraph preceding Theorem 4.3).
Here and hereafter we also assume that for any perturbation  ,
,  ,
,  , are all compact, although this assumption is not necessary in the case that at least one of the operators
, are all compact, although this assumption is not necessary in the case that at least one of the operators  and
and  is compact. In what follows, we define
is compact. In what follows, we define  by convention.
by convention.
Theorem 4.1.
Let  ,
,  , be positive. Suppose that (1.1) is uniformly asymptotically stable and
, be positive. Suppose that (1.1) is uniformly asymptotically stable and  ,
,  are both positive. Then the perturbed (4.1) is still uniformly asymptotically stable if
are both positive. Then the perturbed (4.1) is still uniformly asymptotically stable if

We need the following lemma to prove the theorem.
Lemma 4.2.
Under the same assumptions as in Theorem 4.1 we have

Proof.
Since (1.1) is uniformly asymptotically stable,  , the spectral radius of
, the spectral radius of  , is less than
, is less than  by Theorem 3.5. In particular, it follows that
by Theorem 3.5. In particular, it follows that  is convergent and coincides with
is convergent and coincides with  . Let
. Let  ,
,  , be given. As in the proof of Theorem 3.3, one can see
, be given. As in the proof of Theorem 3.3, one can see  for
for  and
and  ; hence
; hence  , so that
, so that  . Therefore,
. Therefore,

The positivity of  and
and  then implies
then implies

for  , and we thus obtain
, and we thus obtain

which completes the proof.
Proof.
Assume that perturbed (4.1) is not uniformly asymptotically stable for some  satisfying
satisfying  , that is,
, that is,

Then, by Theorem 2.4 there exists a  with
with  such that
such that  is not invertible. So
is not invertible. So  since
since  is compact. Hence, there corresponds an
is compact. Hence, there corresponds an  with
with  satisfying
satisfying  . By virtue of the uniform asymptotic stability of (1.1) we know that
. By virtue of the uniform asymptotic stability of (1.1) we know that  is invertible; and therefore we get
is invertible; and therefore we get

so that  and
and  . In view of Lemma 4.2,
. In view of Lemma 4.2,

which gives  , a contradiction to (4.7). The proof is completed.
, a contradiction to (4.7). The proof is completed.
Let  be the set of all compact operators mapping
be the set of all compact operators mapping  into
into  . We introduce three classes of perturbations defined as
. We introduce three classes of perturbations defined as  ,
,  and
and  . Then the complex, real and positive stability radius of(1.1) under perturbations is defined, respectively, by
. Then the complex, real and positive stability radius of(1.1) under perturbations is defined, respectively, by

where the convention  is used. By definition, it is easy to see that
is used. By definition, it is easy to see that  . On the other hand Theorem 4.1 yields the estimate
. On the other hand Theorem 4.1 yields the estimate

provided that the assumptions of the theorem are satisfied. In fact, these three radii coincide, that is, we have the following.
Theorem 4.3.
Let  ,
,  , be positive. Suppose that (1.1) is uniformly asymptotically stable and
, be positive. Suppose that (1.1) is uniformly asymptotically stable and  ,
,  are both positive. Then
are both positive. Then

Proof.
By the fact  , combined with (4.11), it is sufficient to prove that
, combined with (4.11), it is sufficient to prove that

We may consider the case  since otherwise the theorem is trivial. Suppose by contradiction that (4.13) does not hold. Then there is an
since otherwise the theorem is trivial. Suppose by contradiction that (4.13) does not hold. Then there is an  ,
,  , such that
, such that

By the same reasoning as in the proof of Lemma 4.2, one can see that  and hence
and hence  . Also by (2.10) one may choose
. Also by (2.10) one may choose  with
with  such that
such that

Now let  . Since
. Since  , there exists a positive
, there exists a positive  ,
,  , satisfying
, satisfying  (see [17, Proposition 1.5.7]). Consider a map
(see [17, Proposition 1.5.7]). Consider a map  defined by
defined by

Then, it is easy to see that  and
and  . Hence,
. Hence,

By setting  , we have
, we have

Notice that  because
because  , and that
, and that  , or equivalently
, or equivalently  . Define a perturbation
. Define a perturbation  by
by

Then  . Moreover,
. Moreover,

and in particular  , which means, by Theorem 3.6 (or Theorem 2.4), that the perturbed (4.1) with
, which means, by Theorem 3.6 (or Theorem 2.4), that the perturbed (4.1) with  is not uniformly asymptotically stable. Therefore,
is not uniformly asymptotically stable. Therefore,

which contradicts (4.14). Consequently we must have (4.13), and this completes the proof.
References
Berman A, Plemmons RJ: Nonnegative Matrices in the Mathematical Sciences, Computer Science and Applied Mathematic. Academic Press, New York, NY, USA; 1979:xviii+316.
Luenberger DG: Introduction to Dynamical Systems: Theory, Models and Applications. John Wiley & Sons, New York, NY, USA; 1979.
Commault C, Marchand N (Eds): Positive Systems, Lecture Notes in Control and Information Sciences. Volume 341. Springer, Berlin, Germany; 2006.
Murakami S, Nagabuchi Y: Stability properties and asymptotic almost periodicity for linear Volterra difference equations in a Banach space. Japanese Journal of Mathematics 2005, 31(2):193-223.
Schaefer HH: Banach Lattices and Positive Operators, Die Grundlehren der Mathematischen Wissenschaften. Volume 215. Springer, New York, NY, USA; 1974:xi+376.
Furumochi T, Murakami S, Nagabuchi Y: Volterra difference equations on a Banach space and abstract differential equations with piecewise continuous delays. Japanese Journal of Mathematics 2004, 30(2):387-412.
Furumochi T, Murakami S, Nagabuchi Y: A generalization of Wiener's lemma and its application to Volterra difference equations on a Banach space. Journal of Difference Equations and Applications 2004, 10(13–15):1201-1214.
Furumochi T, Murakami S, Nagabuchi Y: Stabilities in Volterra difference equations on a Banach space. In Differences and Differential Equations, Fields Institute Communications. Volume 42. American Mathematical Society, Providence, RI, USA; 2004:159-175.
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Application, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Elaydi SN: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 2nd edition. Springer, New York, NY, USA; 1999:xviii+427.
Elaydi S, Murakami S: Asymptotic stability versus exponential stability in linear Volterra difference equations of convolution type. Journal of Difference Equations and Applications 1996, 2(4):401-410. 10.1080/10236199608808074
Elaydi S, Murakami S: Uniform asymptotic stability in linear Volterra difference equations. Journal of Difference Equations and Applications 1998, 3(3-4):203-218.
Rudin W: Functional Analysis, International Series in Pure and Applied Mathematics. 2nd edition. McGraw-Hill, New York, NY, USA; 1991:xviii+424.
Wiener J: Generalized Solutions of Functional-Differential Equations. World Scientific, Singapore; 1993:xiv+410.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Ngoc PHA, Naito T, Shin JS, Murakami S: Stability and robust stability of positive linear Volterra difference equations. International Journal of Robust and Nonlinear Control. In press
Meyer-Nieberg P: Banach Lattices, Universitext. Springer, Berlin, Germany; 1991:xvi+395.
Acknowledgment
The first author is partly supported by the Grant-in-Aid for Scientific Research (C), no. 19540203, Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Murakami, S., Nagabuchi, Y. Uniform Asymptotic Stability and Robust Stability for Positive Linear Volterra Difference Equations in Banach Lattices. Adv Differ Equ 2008, 598964 (2008). https://doi.org/10.1155/2008/598964
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/598964
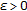 there exists a
there exists a 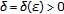 such that if
such that if  and
and  is an initial function on
is an initial function on 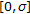 with
with  then
then 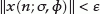 for all
for all  ;
;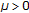 such that, for any
such that, for any 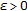 there exists an
there exists an 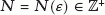 with the property that, if
with the property that, if 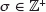 and
and  is an initial function on
is an initial function on 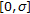 with
with 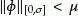 then
then 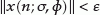 for all
for all  .
. there exists a
there exists a 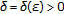 such that if
such that if  and
and 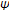 is an initial function on
is an initial function on 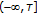 with
with  then
then  for all
for all 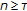 ;
;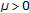 such that, for any
such that, for any  there exists an
there exists an 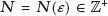 with the property that, if
with the property that, if 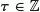 and
and 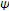 is an initial function on
is an initial function on 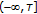 with
with  then
then 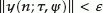 for all
for all 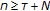 .
.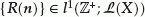 .
. such that
such that  , the operator
, the operator 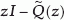 is invertible in
is invertible in 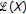 .
.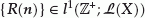
 is invertible in
is invertible in 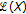 for
for 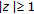 .
.