- Research Article
- Open access
- Published:
Almost-Periodic Weak Solutions of Second-Order Neutral Delay-Differential Equations with Piecewise Constant Argument
Advances in Difference Equations volume 2008, Article number: 816091 (2008)
Abstract
We investigate the existence of almost-periodic weak solutions of second-order neutral delay-differential equations with piecewise constant argument of the form  , where
, where  denotes the greatest integer function,
denotes the greatest integer function,  is a real nonzero constant, and
is a real nonzero constant, and  is almost periodic.
is almost periodic.
1. Introduction and Preliminaries
Differential equations with piecewise constant argument, which were firstly considered by Cooke and Wiener [1], and Shah and Wiener [2], usually describe hybrid dynamical systems (a combination of continuous and discrete) and so combine properties of both differential and difference equations. Over the years, great attention has been paid to the study of the existence of almost-periodic-type solutions of this type of equations. There are many remarkable works on this field (see [3–10] and references therein). Particularly, the second-order neutral delay-differential equations with piecewise constant argument of the form

have been intensively studied for  by different methods, where
by different methods, where  denotes the greatest integer function,
denotes the greatest integer function,  ,
,  are real nonzero constants, and
are real nonzero constants, and  is almost periodic. In [6], Li introduced the concepts of odd-weak solution, even-weak solution, and weak solution of (1.1). Some theorems about the existence of almost-periodic weak solutions were obtained while putting restriction on the function
is almost periodic. In [6], Li introduced the concepts of odd-weak solution, even-weak solution, and weak solution of (1.1). Some theorems about the existence of almost-periodic weak solutions were obtained while putting restriction on the function  . Papers [7, 8] concentrated on dealing with the existence and uniqueness of pseudo-almost-periodic solution by putting some restrictions on the roots of characteristic equation instead of on the function
. Papers [7, 8] concentrated on dealing with the existence and uniqueness of pseudo-almost-periodic solution by putting some restrictions on the roots of characteristic equation instead of on the function  . If
. If  is replaced by a nonlinear function
is replaced by a nonlinear function  , some results about the existence and uniqueness of almost-periodic solution or pseudo-almost-periodic solution were obtained in [8–10].
, some results about the existence and uniqueness of almost-periodic solution or pseudo-almost-periodic solution were obtained in [8–10].
Up to now, there have been no papers concerning the solutions or weak solutions of (1.1) when  . In this paper, we study this case, namely, the equation
. In this paper, we study this case, namely, the equation

In constructing almost-periodic-type solution or weak solution of (1.1) in [6–10], the condition  is essential because it guarantees the convergence of the related series. To investigate such equation as (1.2), we have to give a quite different consideration.
is essential because it guarantees the convergence of the related series. To investigate such equation as (1.2), we have to give a quite different consideration.
Now we give some definitions. Throughout this paper,  ,
,  , and
, and  denote the sets of integers, real, and complex numbers, respectively. The following definitions can be found in any book, say [11], on almost-periodic functions.
denote the sets of integers, real, and complex numbers, respectively. The following definitions can be found in any book, say [11], on almost-periodic functions.
Definition 1.1.
(1). A subset  of
of  is said to be relatively dense in
is said to be relatively dense in  if there exists a number
if there exists a number  such that
such that  for all
for all  .
.
(2). A continuous function  is called almost periodic (abbreviated as
is called almost periodic (abbreviated as  ) if the
) if the  -translation set of
-translation set of 

is relatively dense for each  .
.
Definition 1.2. (1) For a sequence  , define
, define  and call it sequence interval with length
and call it sequence interval with length  . A subset
. A subset  of
of  is said to be relatively dense in
is said to be relatively dense in  if there exists a positive integer
if there exists a positive integer  such that
such that  for all
for all  .
.
(2) A bounded sequence  (resp.,
(resp.,  ) is called an almost-periodic sequence (abbreviated as
) is called an almost-periodic sequence (abbreviated as  ) (resp., abbreviated as
) (resp., abbreviated as  ) if the
) if the  -translation set of
-translation set of 

is relatively dense for each  .
.
As mentioned in [6], we have the following definitions.
Definition 1.3.
A continuous function  is called an odd-weak solution (resp., even-weak solution) of (1.2) if the following conditions are satisfied:
is called an odd-weak solution (resp., even-weak solution) of (1.2) if the following conditions are satisfied:
-
(i)
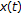 satisfies (1.2) for
satisfies (1.2) for  ,
, 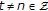 ;
; -
(ii)
the one-sided derivatives
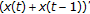 exist at
exist at 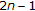 (resp.,
(resp., 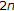 ),
), 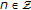 ;
; -
(iii)
the one-sided second-order derivatives
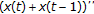 exist at
exist at 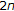 (resp.,
(resp., 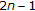 ),
),  .
.
Both odd-weak solution (abbreviated as ow-solution) and even-weak solution (abbreviated as ew-solution) of (1.2) are called weak solution (abbreviated as w-solution) of (1.2). It should be pointed out that if  is an ow-solution (resp., ew-solution) of (1.2), then
is an ow-solution (resp., ew-solution) of (1.2), then  are continuous at
are continuous at  (resp.,
(resp.,  ),
),  ; ow-solution of (1.2) is not equivalent to ew-solution of (1.2);
; ow-solution of (1.2) is not equivalent to ew-solution of (1.2);  is a solution of (1.2) if it is an ow-solution as well as an ew-solution of (1.2).
is a solution of (1.2) if it is an ow-solution as well as an ew-solution of (1.2).
Let  and
and  , then the following hold.
, then the following hold.
Lemma 1.4.
Assume  . The roots of polynomials
. The roots of polynomials  are of modules different from 1,
are of modules different from 1,  .
.
Proof.
It is clear that 1 and −1 are not the roots of  because
because  ,
,  . Denote the three roots of
. Denote the three roots of  by
by  , without loss of generality, let
, without loss of generality, let  ,
,  , here
, here  is a real constant, thus we obtain
is a real constant, thus we obtain  , which is impossible. So, the modules of roots of polynomial
, which is impossible. So, the modules of roots of polynomial  are not 1.
are not 1.
If  , it is obvious that the result holds for
, it is obvious that the result holds for  . If
. If  , denote the three roots of
, denote the three roots of  by
by  , without loss of generality, let
, without loss of generality, let  ,
,  , here
, here  is a real constant, then we have
is a real constant, then we have

This implies that  and contradicts the hypothesis. The proof is complete.
and contradicts the hypothesis. The proof is complete.
The rest of this paper is organized as follows. Section 2 is devoted to the main theorems and their proofs. In Section 3, some examples are given to explain our results and illuminate the relationship among solution, ow-solution, and ew-solution.
2. The Main Results
Let

To present the main results of this paper, we need the following assumption.
(H)  is such that there exists
is such that there exists  such that
such that  , for all
, for all  .
.
Remark 2.1. (1)  is a translation invariant Banach space. For every
is a translation invariant Banach space. For every  , one has
, one has  too. Set
too. Set  , then
, then  satisfies (H), and therefore there exist a great number of functions satisfying the assumption (H). (2) Reference [5] uses an assumption similar to (H) implicitly.
satisfies (H), and therefore there exist a great number of functions satisfying the assumption (H). (2) Reference [5] uses an assumption similar to (H) implicitly.
Let  . We have the following lemma.
. We have the following lemma.
Lemma 2.2.
Under the assumption (H), one has  .
.
Proof.
By (H), there exists  such that
such that  ,
,  . Let
. Let  and
and  , it is easy to verify that
, it is easy to verify that  ,
, ,
,  ,
,  ,
, ,
,  ,
,  , and
, and  ,
,  , for all
, for all  that is,
that is,  ,
,  . Set
. Set  , similarly we can obtain
, similarly we can obtain  ,
,  , and
, and  , for all
, for all  that is,
that is,  .
.
Lemma 2.3.
Suppose that  is a Banach space,
is a Banach space,  denotes the set of bounded linear operators from
denotes the set of bounded linear operators from  to
to  ,
,  and
and  , then
, then  is bounded invertible and
is bounded invertible and

where  ,
,  is an identical operator.
is an identical operator.
The proof of Lemma 2.3 can be found in any book of functional analysis. We remark that if  is a linear operator and its inverse exists, then
is a linear operator and its inverse exists, then  is also a linear operator.
is also a linear operator.
To get w-solutions or solutions of (1.2), we start with its corresponding difference equations.
Suppose that  is an ow-solution of (1.2), then
is an ow-solution of (1.2), then  satisfies the three conditions in Definition 1.3. By a process of integrating (1.2) two times in
satisfies the three conditions in Definition 1.3. By a process of integrating (1.2) two times in  as in [6–10], we can easily get
as in [6–10], we can easily get

Similarly if  is an ew-solution of (1.2), by the process of integrating (1.2) two times in
is an ew-solution of (1.2), by the process of integrating (1.2) two times in  , we get
, we get

These lead to the difference equations


From the analysis above, one sees that if  is an ow-solution (resp., ew-solution) of (1.2), then one gets (2.5) (resp., (2.6)); if
is an ow-solution (resp., ew-solution) of (1.2), then one gets (2.5) (resp., (2.6)); if  is a solution of (1.2), then one gets both (2.5) and (2.6). Conversely, we will show that the w-solutions or solutions of (1.2) are obtained via the solutions of (2.5) and (2.6). In order to get the solutions of (2.5) and (2.6), we will consider the following difference equations:
is a solution of (1.2), then one gets both (2.5) and (2.6). Conversely, we will show that the w-solutions or solutions of (1.2) are obtained via the solutions of (2.5) and (2.6). In order to get the solutions of (2.5) and (2.6), we will consider the following difference equations:


Notice that for any sequences  , and
, and  , one has
, one has  . Especially,
. Especially,  In virtue of studying (2.7) and (2.8), we have the following theorem.
In virtue of studying (2.7) and (2.8), we have the following theorem.
Theorem 2.4.
Under the assumption (H), (2.7) (resp., (2.8)) has a unique solution  (resp.,
(resp.,  ).
).
Proof.
As the proof of [7, Theorem 9], define  by
by  , where
, where  is the Banach space consisting of all bounded sequences
is the Banach space consisting of all bounded sequences  in
in  with
with  . Notice Lemmas 1.4 and 2.3, we know that (2.7) has a unique solution
. Notice Lemmas 1.4 and 2.3, we know that (2.7) has a unique solution  . By the process of proving Lemma 2.2, we have
. By the process of proving Lemma 2.2, we have  that is,
that is,  where
where  (this follows in the same way as [7, Theorem 9]). Therefore, (2.7) has a unique solution
(this follows in the same way as [7, Theorem 9]). Therefore, (2.7) has a unique solution  .
.
Similarly, (2.8) has a unique solution  and
and  , that is,
, that is,  where
where  . Therefore, (2.8) has a unique solution
. Therefore, (2.8) has a unique solution  . This completes the proof.
. This completes the proof.
Remark 2.5. (i) In Theorem 2.4, since  and
and  , we can easily get
, we can easily get


It must be stressed that (2.9) and (2.10) are important, since they can guarantee the continuity of the w-solutions or solutions of (1.2) constructed in Theorems 2.6, 2.7, and 2.8.
(ii) Let  with
with  satisfying (2.9)
satisfying (2.9)  , and
, and  with
with  satisfying (2.10)
satisfying (2.10)  . Notice the fact that the solution of (2.7) (resp., (2.8)) must be a solution of (2.5) (resp., (2.6)), it is false conversely. So, suppose the assumption (H) holds, it follows from Theorem 2.4 that (2.5) (resp., (2.6)) has solution
. Notice the fact that the solution of (2.7) (resp., (2.8)) must be a solution of (2.5) (resp., (2.6)), it is false conversely. So, suppose the assumption (H) holds, it follows from Theorem 2.4 that (2.5) (resp., (2.6)) has solution  (resp.,
(resp.,  ). Moreover, such solutions may not be unique. See Example 3.1 at the end of this paper.
). Moreover, such solutions may not be unique. See Example 3.1 at the end of this paper.
In the following, we focus on seeking the almost-periodic w-solutions or solutions of (1.2) via the almost-periodic sequence solutions of (2.5) and (2.6). As mentioned above, it is due to  that, to get almost-periodic w-solutions or solutions of (1.2), we have to use a way quite different from [6–10]. Our main idea is to construct solutions or w-solutions of (1.2) piecewise. It seems that this is a new technique.
that, to get almost-periodic w-solutions or solutions of (1.2), we have to use a way quite different from [6–10]. Our main idea is to construct solutions or w-solutions of (1.2) piecewise. It seems that this is a new technique.
Without loss of generality, suppose that  (resp.,
(resp.,  ) is an arbitrary solution of (2.5) (resp., (2.6)). To prove the following theorems, we need to introduce some notations firstly:
) is an arbitrary solution of (2.5) (resp., (2.6)). To prove the following theorems, we need to introduce some notations firstly:

where  and
and  . It can be easily verified that
. It can be easily verified that 
For the existence of the almost-periodic ow-solution of (1.2), we have the following.
Theorem 2.6.
Under the assumption (H), (1.2) has an ow-solution  such that
such that  .
.
Proof.
Under the assumption (H), define  as
as

where

From (2.9), it follows that  is continuous on
is continuous on  and
and  ,
,  . Moreover, for
. Moreover, for  ,
,  , one has
, one has  ; for
; for  ,
,  , one has
, one has  . By simple calculation, for
. By simple calculation, for  ,
,  , we have
, we have

Note that  , this implies that the one-sided derivatives
, this implies that the one-sided derivatives  exist at
exist at 
 . Since
. Since  , the second-order derivatives
, the second-order derivatives  are continuous at
are continuous at  ,
,  . Therefore,
. Therefore,  is an ow-solution of (1.2) such that
is an ow-solution of (1.2) such that  ,
,  . Furthermore, it is easy to check that
. Furthermore, it is easy to check that  is almost periodic, we omit the details. The proof is complete.
is almost periodic, we omit the details. The proof is complete.
For the existence of the almost-periodic ew-solution of (1.2), we have the following.
Theorem 2.7.
Under the assumption (H), (1.2) has an ew-solution  such that
such that  .
.
Proof.
Under the assumption (H), define  as
as

where

From (2.10), it follows that  is continuous on
is continuous on  and
and  ,
,  . The rest of the proof is similar to that of Theorem 2.6, we omit the details.
. The rest of the proof is similar to that of Theorem 2.6, we omit the details.
For the existence of almost-periodic solution of (1.2), we have the following.
Theorem 2.8.
Under the assumption (H), if  is the common solution of (2.5) and (2.6), then (1.2) has a solution
is the common solution of (2.5) and (2.6), then (1.2) has a solution  such that
such that  ,
,  . If
. If  replaces
replaces  , the conclusion is still true.
, the conclusion is still true.
Proof.
Since  and
and  are solutions of (2.5) and (2.9) respectively, and they are also solutions of (2.6) and (2.10), respectively, it follows from Theorems 2.6 and 2.7 that, by simple calculation, the almost-periodic ow-solution
are solutions of (2.5) and (2.9) respectively, and they are also solutions of (2.6) and (2.10), respectively, it follows from Theorems 2.6 and 2.7 that, by simple calculation, the almost-periodic ow-solution  constructed as the proof of Theorem 2.6 with
constructed as the proof of Theorem 2.6 with  ,
,  , is the same as the almost-periodic ew-solution
, is the same as the almost-periodic ew-solution  constructed as the proof of Theorem 2.7 with
constructed as the proof of Theorem 2.7 with  ,
,  . This implies
. This implies  is an almost-periodic solution of (1.2) such that
is an almost-periodic solution of (1.2) such that  ,
,  . If
. If  replaces
replaces  , the proof is similar, we omit the details.
, the proof is similar, we omit the details.
Remark 2.9.
As mentioned above, an ow-solution of (1.2) is not equivalent to an ew-solution of (1.2), and a solution of (1.2) is an ow-solution of (1.2) as well as an ew-solution of (1.2). See the examples in Section 3.
The following theorem is usually used for judging whether or not a w-solution of (1.2) is a solution of (1.2).
Theorem 2.10.
Suppose that  is a solution of (1.2), then
is a solution of (1.2), then

Proof.
If  is a solution of (1.2), then
is a solution of (1.2), then  must be common solution of (2.5) and (2.6). Moreover, (2.6) is equivalent to
must be common solution of (2.5) and (2.6). Moreover, (2.6) is equivalent to

Substituting  into both the above equation and (2.5), then add the resulting equations to get the result.
into both the above equation and (2.5), then add the resulting equations to get the result.
3. Some Examples
In this section, we first explain how to get almost periodic w-solutions and solutions of (1.2) specifically. And then, we present two examples: in Example 3.1, we aim mainly to obtain the almost-periodic solution, and in Example 3.2, we obtain the almost-periodic ow-solution and ew-solution. Consequently, the relationship among ow-solution, ew-solution, and solution is shown. Besides, Example 3.1 also illuminates that the solutions in  (resp.,
(resp.,  ) of (2.5) (resp., (2.6)) may not be unique.
) of (2.5) (resp., (2.6)) may not be unique.
Under the assumption (H), it follows from the proof of Theorem 2.6 (resp., 2.7) that we can get almost-periodic ow-solution (resp., ew-solution) of (1.2) by the following three steps.
-
(i)
Calculate
 ,
, 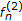 ,
,  ,
, 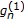 ,
,  ,
, 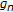 ,
,  ,
, 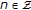 , and
, and 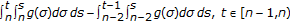 ,
, 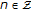 .
. -
(ii)
Seek the solution
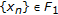 (resp.,
(resp., 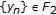 ) of (2.5) (resp., (2.6)). Calculate
) of (2.5) (resp., (2.6)). Calculate 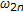 and
and  (resp.,
(resp., 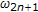 and
and 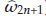 ).
). -
(iii)
By the proof of Theorem 2.6 (resp., 2.7), we get the almost-periodic ow-solution
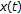 (resp., ew-solution
(resp., ew-solution 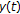 ) such that
) such that 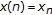 , (resp.,
, (resp., 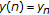 ),
),  .
.
On the other hand, it follows from the proof of Theorem 2.8 that we can get the almost-periodic solution by the following steps.
-
(i)
Seek the solution
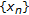 in
in  which is the common solution of (2.5) and (2.6). Calculate
which is the common solution of (2.5) and (2.6). Calculate 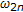 ,
, 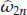 ,
, 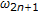 , and
, and 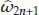 .
. -
(ii)
Find the almost periodic ow-solution
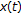 such that
such that  ,
,  or ew-solution
or ew-solution  such that
such that  ,
, 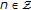 by the above methods. From Theorem 2.8, we know they are the same, that is, it must be the almost periodic solution.
by the above methods. From Theorem 2.8, we know they are the same, that is, it must be the almost periodic solution.
The following example shows that a solution of (1.2) is an ow-solution of (1.2) as well as an ew-solution of (1.2), and the solutions in  (resp.,
(resp.,  ) of (2.5) (resp., (2.6)) may not unique.
) of (2.5) (resp., (2.6)) may not unique.
Example 3.1.
Let  ,
,  , and
, and  , then
, then  , and
, and  , for all
, for all  that is,
that is,  satisfy the assumption (H). By simple calculation, we can obtain
satisfy the assumption (H). By simple calculation, we can obtain  ,
,  ,
,  ,
,  , and
, and  ,
,  , for all
, for all  .
.
-
(i)
We construct the almost-periodic solution of (1.2) as the proof of Theorem 2.8.
Let

then  is the common solution of (2.5) and (2.6). Calculate
is the common solution of (2.5) and (2.6). Calculate  ,
,  ,
,  ,
,  by the formulas mentioned above, we obtain
by the formulas mentioned above, we obtain  ,
,  ,
,  Obviously,
Obviously,  and
and  . Define the ow-solution and the ew-solution as the proofs of Theorems 2.6 and 2.7, respectively, it follows from the proof of Theorem 2.8 that they are the same, so it must be a solution, that is, an ow-solution as well as an ew-solution. Specifically, it can be expressed as
. Define the ow-solution and the ew-solution as the proofs of Theorems 2.6 and 2.7, respectively, it follows from the proof of Theorem 2.8 that they are the same, so it must be a solution, that is, an ow-solution as well as an ew-solution. Specifically, it can be expressed as

where

It is easy to check that  is an almost-periodic solution of (1.2) such that
is an almost-periodic solution of (1.2) such that  ,
,  .
.
-
(ii)
We show that
 (resp.,
(resp., 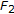 ) is not unique solution of (2.5) (resp., (2.6)).
) is not unique solution of (2.5) (resp., (2.6)).
Let

Obviously,  is another solution of (2.5).
is another solution of (2.5).
Let  and
and

where  is an arbitrary constant, then it is clear that
is an arbitrary constant, then it is clear that  is another solution of (2.6).
is another solution of (2.6).
The following example shows that ow-solutions and ew-solutions of (1.2) are not equivalent.
Example 3.2.
As [6], let  ,
,  , for all
, for all  , then
, then  , setting
, setting  , then
, then  and
and  , for all
, for all  that is, the assumption (H) holds. By simple calculation, we can obtain
that is, the assumption (H) holds. By simple calculation, we can obtain  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
-
(i)
We construct the almost-periodic ow-solution of (1.2) as the proof of Theorem 2.6.
Let

then  is the solution of (2.5). Calculate
is the solution of (2.5). Calculate  as the formulas mentioned above, we obtain
as the formulas mentioned above, we obtain  ,
,  Obviously,
Obviously,  ,
,  .
.
Define the ow-solution  as
as

where

It is easy to check that  is an almost-periodic ow-solution of (1.2). Since
is an almost-periodic ow-solution of (1.2). Since  is not solution of (2.17), it follows from Theorem 2.10 that
is not solution of (2.17), it follows from Theorem 2.10 that  is not solution of (1.2) and consequently,
is not solution of (1.2) and consequently,  is not an ew-solution of (1.2).
is not an ew-solution of (1.2).
-
(ii)
Similarly to (i), by Theorem 2.7, we construct the almost-periodic ew-solution of (1.2).
Let  and
and

where  is an arbitrary constant, then
is an arbitrary constant, then  is the solution of (2.6). Calculate
is the solution of (2.6). Calculate  as the formulas mentioned above, we obtain
as the formulas mentioned above, we obtain  ,
,  Obviously,
Obviously,  .
.
Define the ew-solution  as
as

where

It is easy to verify that  is an almost-periodic ew-solution of (1.2). Since
is an almost-periodic ew-solution of (1.2). Since  is not solution of (2.17), it follows from Theorem 2.10 that
is not solution of (2.17), it follows from Theorem 2.10 that  is not solution of (1.2) and consequently,
is not solution of (1.2) and consequently,  is not an ow-solution of (1.2).
is not an ow-solution of (1.2).
References
Cooke KL, Wiener J: Retarded differential equations with piecewise constant delays. Journal of Mathematical Analysis and Applications 1984, 99(1):265-297. 10.1016/0022-247X(84)90248-8
Shah SM, Wiener J: Advanced differential equations with piecewise constant argument deviations. International Journal of Mathematics and Mathematical Sciences 1983, 6(4):671-703. 10.1155/S0161171283000599
Seifert G: Second-order neutral delay-differential equations with piecewise constant time dependence. Journal of Mathematical Analysis and Applications 2003, 281(1):1-9.
Piao DX: Almost periodic solutions of neutral differential difference equations with piecewise constant arguments. Acta Mathematica Sinica 2002, 18(2):263-276.
Li H-X: Almost periodic solutions of second-order neutral delay-differential equations with piecewise constant arguments. Journal of Mathematical Analysis and Applications 2004, 298(2):693-709. 10.1016/j.jmaa.2004.05.034
Li H-X: Almost periodic weak solutions of neutral delay-differential equations with piecewise constant argument. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(3):530-545. 10.1016/j.na.2005.05.041
Dads EA, Lhachimi L: New approach for the existence of pseudo almost periodic solutions for some second order differential equation with piecewise constant argument. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(6):1307-1324. 10.1016/j.na.2005.06.037
Yuan R: Pseudo-almost periodic solutions of second-order neutral delay differential equations with piecewise constant argument. Nonlinear Analysis: Theory, Methods & Applications 2000, 41(7-8):871-890. 10.1016/S0362-546X(98)00316-2
Yuan R: Existence of almost periodic solutions of second order neutral delay differential equations with piecewise constant argument. Science in China Series A 1998, 41(3):232-241.
Li Z, He M: The existence of almost periodic solutions of second order neutral differential equations with piecewise constant argument. Northeastern Mathematical Journal 1999, 15(3):369-378.
Zhang C: Almost Periodic Type Functions and Ergodicity. Science Press/Kluwer Academic Publishers, Beijing, China; 2003:xii+355.
Acknowledgment
The research is supported by the NSF of China no. 10671047.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, L., Zhang, C. Almost-Periodic Weak Solutions of Second-Order Neutral Delay-Differential Equations with Piecewise Constant Argument. Adv Differ Equ 2008, 816091 (2008). https://doi.org/10.1155/2008/816091
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/816091
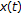 satisfies (1.2) for
satisfies (1.2) for  ,
, 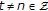 ;
;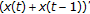 exist at
exist at 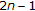 (resp.,
(resp., 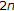 ),
), 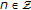 ;
;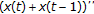 exist at
exist at 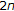 (resp.,
(resp., 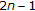 ),
),  .
. ,
, 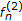 ,
,  ,
, 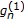 ,
,  ,
, 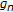 ,
,  ,
, 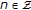 , and
, and 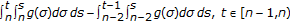 ,
, 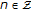 .
.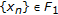 (resp.,
(resp., 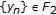 ) of (2.5) (resp., (2.6)). Calculate
) of (2.5) (resp., (2.6)). Calculate 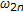 and
and  (resp.,
(resp., 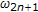 and
and 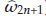 ).
).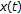 (resp., ew-solution
(resp., ew-solution 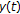 ) such that
) such that 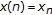 , (resp.,
, (resp., 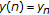 ),
),  .
.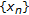 in
in  which is the common solution of (2.5) and (2.6). Calculate
which is the common solution of (2.5) and (2.6). Calculate 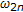 ,
, 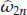 ,
, 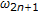 , and
, and 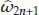 .
.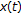 such that
such that  ,
,  or ew-solution
or ew-solution  such that
such that  ,
, 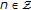 by the above methods. From Theorem 2.8, we know they are the same, that is, it must be the almost periodic solution.
by the above methods. From Theorem 2.8, we know they are the same, that is, it must be the almost periodic solution. (resp.,
(resp., 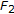 ) is not unique solution of (2.5) (resp., (2.6)).
) is not unique solution of (2.5) (resp., (2.6)).