- Research Article
- Open access
- Published:
Neural Network Adaptive Control for Discrete-Time Nonlinear Nonnegative Dynamical Systems
Advances in Difference Equations volume 2008, Article number: 868425 (2008)
Abstract
Nonnegative and compartmental dynamical system models are derived from mass and energy balance considerations that involve dynamic states whose values are nonnegative. These models are widespread in engineering and life sciences, and they typically involve the exchange of nonnegative quantities between subsystems or compartments, wherein each compartment is assumed to be kinetically homogeneous. In this paper, we develop a neuroadaptive control framework for adaptive set-point regulation of discrete-time nonlinear uncertain nonnegative and compartmental systems. The proposed framework is Lyapunov-based and guarantees ultimate boundedness of the error signals corresponding to the physical system states and the neural network weighting gains. In addition, the neuroadaptive controller guarantees that the physical system states remain in the nonnegative orthant of the state space for nonnegative initial conditions.
1. Introduction
Neural networks have provided an ideal framework for online identification and control of many complex uncertain engineering systems because of their great flexibility in approximating a large class of continuous maps and their adaptability due to their inherently parallel architecture. Even though neuroadaptive control has been applied to numerous engineering problems, neuroadaptive methods have not been widely considered for problems involving systems with nonnegative state and control constraints [1, 2]. Such systems are commonly referred to as nonnegative dynamical systems in the literature [3–8]. A subclass of nonnegative dynamical systems are compartmental systems [8–18]. Compartmental systems involve dynamical models that are characterized by conservation laws (e.g., mass and energy) capturing the exchange of material between coupled macroscopic subsystems known as compartments. The range of applications of nonnegative systems and compartmental systems includes pharmacological systems, queuing systems, stochastic systems (whose state variables represent probabilities), ecological systems, economic systems, demographic systems, telecommunications systems, and transportation systems, to cite but a few examples. Due to the severe complexities, nonlinearities, and uncertainties inherent in these systems, neural networks provide an ideal framework for online adaptive control because of their parallel processing flexibility and adaptability.
In this paper, we extend the results of [2] to develop a neuroadaptive control framework for discrete-time nonlinear uncertain nonnegative and compartmental systems. The proposed framework is Lyapunov-based and guarantees ultimate boundedness of the error signals corresponding to the physical system states as well as the neural network weighting gains. The neuroadaptive controllers are constructed without requiring knowledge of the system dynamics while guaranteeing that the physical system states remain in the nonnegative orthant of the state space. The proposed neuro control architecture is modular in the sense that if a nominal linear design model is available, the neuroadaptive controller can be augmented to the nominal design to account for system nonlinearities and system uncertainty. Furthermore, since in certain applications of nonnegative and compartmental systems (e.g., pharmacological systems for active drug administration) control (source) inputs as well as the system states need to be nonnegative, we also develop neuroadaptive controllers that guarantee the control signal as well as the physical system states remain nonnegative for nonnegative initial conditions.
The contents of the paper are as follows. In Section 2, we provide mathematical preliminaries on nonnegative dynamical systems that are necessary for developing the main results of this paper. In Section 3, we develop new Lyapunov-like theorems for partial boundedness and partial ultimate boundedness for nonlinear dynamical systems necessary for obtaining less conservative ultimate bounds for neuroadaptive controllers as compared to ultimate bounds derived using classical boundedness and ultimate boundedness notions. In Section 4, we present our main neuroadaptive control framework for adaptive set-point regulation of nonlinear uncertain nonnegative and compartmental systems. In Section 5, we extend the results of Section 4 to the case where control inputs are constrained to be nonnegative. Finally, in Section 6 we draw some conclusions.
2. Mathematical Preliminaries
In this section we introduce notation, several definitions, and some key results concerning linear and nonlinear discrete-time nonnegative dynamical systems [19] that are necessary for developing the main results of this paper. Specifically, for  we write
we write  (resp.,
(resp.,  ) to indicate that every component of
) to indicate that every component of  is nonnegative (resp., positive). In this case, we say that
is nonnegative (resp., positive). In this case, we say that  is nonnegative or positive, respectively. Likewise,
is nonnegative or positive, respectively. Likewise,  is nonnegative or positive if every entry of
is nonnegative or positive if every entry of  is nonnegative or positive, respectively, which is written as
is nonnegative or positive, respectively, which is written as  or
or  , respectively. In this paper it is important to distinguish between a square nonnegative (resp., positive) matrix and a nonnegative-definite (resp., positive-definite) matrix. Let
, respectively. In this paper it is important to distinguish between a square nonnegative (resp., positive) matrix and a nonnegative-definite (resp., positive-definite) matrix. Let  and
and  denote the nonnegative and positive orthants of
denote the nonnegative and positive orthants of  , that is, if
, that is, if  , then
, then  and
and  are equivalent, respectively, to
are equivalent, respectively, to  and
and  . Finally, we write
. Finally, we write  to denote transpose,
to denote transpose,  for the trace operator,
for the trace operator,  (resp.,
(resp.,  ) to denote the minimum (resp., maximum) eigenvalue of a Hermitian matrix,
) to denote the minimum (resp., maximum) eigenvalue of a Hermitian matrix,  for a vector norm, and
for a vector norm, and  for the set of all nonnegative integers. The following definition introduces the notion of a nonnegative (resp., positive) function.
for the set of all nonnegative integers. The following definition introduces the notion of a nonnegative (resp., positive) function.
Definition 2.1.
A real function  is a nonnegative (resp., positive) function if
is a nonnegative (resp., positive) function if  (resp.,
(resp.,  ),
),  .
.
The following theorems give necessary and sufficient conditions for asymptotic stability of the discrete-time linear nonnegative dynamical system

where  is nonnegative and
is nonnegative and  , using linear and quadratic Lyapunov functions, respectively.
, using linear and quadratic Lyapunov functions, respectively.
Theorem 2.2 (see [19]).
Consider the linear dynamical system  given by (2.1) where
given by (2.1) where  is nonnegative. Then
is nonnegative. Then  is asymptotically stable if and only if there exist vectors
is asymptotically stable if and only if there exist vectors  such that
such that  and
and  satisfy
satisfy

Consider the linear dynamical system  given by (2.1) where
given by (2.1) where  is nonnegative. Then
is nonnegative. Then  is asymptotically stable if and only if there exist a positive diagonal matrix
is asymptotically stable if and only if there exist a positive diagonal matrix  and an
and an  positive-definite matrix
positive-definite matrix  such that
such that

Next, consider the controlled discrete-time linear dynamical system

where

 is nonnegative and
is nonnegative and  is nonnegative such that rank
is nonnegative such that rank  . The following theorem shows that discrete-time linear stabilizable nonnegative systems possess asymptotically stable zero dynamics with
. The following theorem shows that discrete-time linear stabilizable nonnegative systems possess asymptotically stable zero dynamics with  viewed as the output. For the statement of this result, let
viewed as the output. For the statement of this result, let  denote the spectrum of
denote the spectrum of  , let
, let  , and let
, and let  in (2.4) be partitioned as
in (2.4) be partitioned as

where  ,
,  ,
,  , and
, and  are nonnegative matrices.
are nonnegative matrices.
Theorem 2.4.
Consider the discrete-time linear dynamical system  given by (2.4), where
given by (2.4), where  is nonnegative and partitioned as in (2.6), and
is nonnegative and partitioned as in (2.6), and  is nonnegative and is partitioned as in (2.5) with rank
is nonnegative and is partitioned as in (2.5) with rank  . Then there exists a gain matrix
. Then there exists a gain matrix  such that
such that  is nonnegative and asymptotically stable if and only if
is nonnegative and asymptotically stable if and only if  is asymptotically stable.
is asymptotically stable.
Proof.
First, let  be partitioned as
be partitioned as  , where
, where  and
and  , and note that
, and note that

Assume that  is nonnegative and asymptotically stable, and suppose that, ad absurdum,
is nonnegative and asymptotically stable, and suppose that, ad absurdum,  is not asymptotically stable. Then, it follows from Theorem 2.2 that there does not exist a positive vector
is not asymptotically stable. Then, it follows from Theorem 2.2 that there does not exist a positive vector  such that
such that  . Next, since
. Next, since  is nonnegative it follows that
is nonnegative it follows that  for any positive vector
for any positive vector  . Thus, there does not exist a positive vector
. Thus, there does not exist a positive vector  such that
such that  , and hence, it follows from Theorem 2.2 that
, and hence, it follows from Theorem 2.2 that  is not asymptotically stable leading to a contradiction. Hence,
is not asymptotically stable leading to a contradiction. Hence,  is asymptotically stable. Conversely, suppose that
is asymptotically stable. Conversely, suppose that  is asymptotically stable. Then taking
is asymptotically stable. Then taking  and
and  , where
, where  is nonnegative and asymptotically stable, it follows that
is nonnegative and asymptotically stable, it follows that 
 , and hence,
, and hence,  is nonnegative and asymptotically stable.
is nonnegative and asymptotically stable.
Next, consider the discrete-time nonlinear dynamical system

where  ,
,  is an open subset of
is an open subset of  with
with  , and
, and  is continuous on
is continuous on  . Recall that the point
. Recall that the point  is an equilibrium point of (2.8) if
is an equilibrium point of (2.8) if  . Furthermore, a subset
. Furthermore, a subset  is an invariant set with respect to (2.8) if
is an invariant set with respect to (2.8) if  contains the orbits of all its points. The following definition introduces the notion of nonnegative vector fields [19].
contains the orbits of all its points. The following definition introduces the notion of nonnegative vector fields [19].
Definition 2.5.
Let  , where
, where  is an open subset of
is an open subset of  that contains
that contains  . Then
. Then  is nonnegative with respect to
is nonnegative with respect to ,
,  , if
, if  for all
for all  , and
, and  .
.  is nonnegative if
is nonnegative if  for all
for all  , and
, and  .
.
Note that if  , where
, where  , then
, then  is nonnegative if and only if
is nonnegative if and only if  is nonnegative [19].
is nonnegative [19].
Proposition 2.6 (see [19]).
Suppose  . Then
. Then  is an invariant set with respect to (2.8) if and only if
is an invariant set with respect to (2.8) if and only if  is nonnegative.
is nonnegative.
In this paper, we consider controlled discrete-time nonlinear dynamical systems of the form

where  ,
,  ,
,  ,
,  ,
,  is continuous and satisfies
is continuous and satisfies  , and
, and  is continuous.
is continuous.
The following definition and proposition are needed for the main results of the paper.
Definition 2.7.
The discrete-time nonlinear dynamical system given by (2.9) is nonnegative if for every  and
and  ,
,  , the solution
, the solution  ,
,  , to (2.9) is nonnegative.
, to (2.9) is nonnegative.
Proposition 2.8 (see [19]).
The discrete-time nonlinear dynamical system given by (2.9) is nonnegative if  and
and  ,
,  .
.
It follows from Proposition 2.8 that a nonnegative input signal  ,
,  , is sufficient to guarantee the nonnegativity of the state of (2.9).
, is sufficient to guarantee the nonnegativity of the state of (2.9).
Next, we present a time-varying extension to Proposition 2.8 needed for the main theorems of this paper. Specifically, we consider the time-varying system

where  is continuous in
is continuous in  and
and  on
on  and
and  ,
,  , and
, and  is continuous. For the following result, the definition of nonnegativity holds with (2.9) replaced by (2.10).
is continuous. For the following result, the definition of nonnegativity holds with (2.9) replaced by (2.10).
Proposition 2.9.
Consider the time-varying discrete-time dynamical system (2.10) where  is continuous on
is continuous on  for all
for all  and
and  is continuous on
is continuous on  for all
for all  . If for every
. If for every  ,
,  is nonnegative and
is nonnegative and  is nonnegative, then the solution
is nonnegative, then the solution  ,
,  , to (2.10) is nonnegative.
, to (2.10) is nonnegative.
Proof.
The result is a direct consequence of Proposition 2.8 by equivalently representing the time-varying discrete-time system (2.10) as an autonomous discrete-time nonlinear system by appending another state to represent time. Specifically, defining  and
and  , it follows that the solution
, it follows that the solution  ,
,  , to (2.10) can be equivalently characterized by the solution
, to (2.10) can be equivalently characterized by the solution  ,
,  , where
, where  , to the discrete-time nonlinear autonomous system
, to the discrete-time nonlinear autonomous system


where  . Now, since
. Now, since  ,
,  , for
, for  , and
, and  , the result is a direct consequence of Proposition 2.8.
, the result is a direct consequence of Proposition 2.8.
3. Partial Boundedness and Partial Ultimate Boundedness
In this section, we present Lyapunov-like theorems for partial boundedness and partial ultimate boundedness of discrete-time nonlinear dynamical systems. These notions allow us to develop less conservative ultimate bounds for neuroadaptive controllers as compared to ultimate bounds derived using classical boundedness and ultimate boundedness notions. Specifically, consider the discrete-time nonlinear autonomous interconnected dynamical system


where  ,
,  is an open set such that
is an open set such that  ,
,  ,
,  is such that, for every
is such that, for every  ,
,  and
and  is continuous in
is continuous in  , and
, and  is continuous. Note that under the above assumptions the solution
is continuous. Note that under the above assumptions the solution  to (3.1) and (3.2) exists and is unique over
to (3.1) and (3.2) exists and is unique over  .
.
Definition 3.1 (see [20]).
-
(i)
The discrete-time nonlinear dynamical system (3.1) and (3.2) is bounded with respect to
 uniformly in
uniformly in if there exists
if there exists  such that, for every
such that, for every  , there exists
, there exists  such that
such that  implies
implies 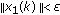 for all
for all  . The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to
. The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to uniformly in
uniformly in if, for every
if, for every  , there exists
, there exists 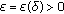 such that
such that  implies
implies  for all
for all  .
. -
(ii)
The discrete-time nonlinear dynamical system (3.1) and (3.2) is ultimately bounded with respect to
 uniformly in
uniformly in  with ultimate bound
with ultimate bound  if there exists
if there exists 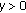 such that, for every
such that, for every 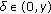 , there exists
, there exists 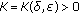 such that
such that  implies
implies  ,
,  . The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to
. The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound
with ultimate bound  if, for every
if, for every 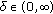 , there exists
, there exists 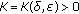 such that
such that  implies
implies 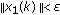 ,
, 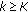 .
.
Note that if a discrete-time nonlinear dynamical system is (globally) bounded with respect to  uniformly in
uniformly in  , then there exists
, then there exists  such that it is (globally) ultimately bounded with respect to
such that it is (globally) ultimately bounded with respect to  uniformly in
uniformly in  with an ultimate bound
with an ultimate bound  . Conversely, if a discrete-time nonlinear dynamical system is (globally) ultimately bounded with respect to
. Conversely, if a discrete-time nonlinear dynamical system is (globally) ultimately bounded with respect to  uniformly in
uniformly in  with an ultimate bound
with an ultimate bound  , then it is (globally) bounded with respect to
, then it is (globally) bounded with respect to  uniformly in
uniformly in  . The following results present Lyapunov-like theorems for boundedness and ultimate boundedness for discrete-time nonlinear systems. For these results define
. The following results present Lyapunov-like theorems for boundedness and ultimate boundedness for discrete-time nonlinear systems. For these results define  , where
, where  and
and  is a given continuous function. Furthermore, let
is a given continuous function. Furthermore, let  ,
,  ,
,  , denote the open ball centered at
, denote the open ball centered at  with radius
with radius  and let
and let  denote the closure of
denote the closure of  , and recall the definitions of class-
, and recall the definitions of class- , class-
, class- , and class-
, and class- functions [20].
functions [20].
Theorem 3.2.
Consider the discrete-time nonlinear dynamical system (3.1) and (3.2). Assume that there exist a continuous function  and class-
and class- functions
functions  and
and  such that
such that


where  is such that
is such that  . Furthermore, assume that
. Furthermore, assume that  exists. Then the discrete-time nonlinear dynamical system (3.1) and (3.2) is bounded with respect to
exists. Then the discrete-time nonlinear dynamical system (3.1) and (3.2) is bounded with respect to  uniformly in
uniformly in  . Furthermore, for every
. Furthermore, for every  ,
,  implies that
implies that  ,
,  , where
, where

 , and
, and  . If, in addition,
. If, in addition,  and
and  is a class-
is a class- function, then the discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to
function, then the discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to  uniformly in
uniformly in  and for every
and for every  ,
,  ,
,  , where
, where  is given by (3.5) with
is given by (3.5) with  .
.
Proof.
See [20, page 786].
Theorem 3.3.
Consider the discrete-time nonlinear dynamical system (3.1) and (3.2). Assume there exist a continuous function  and class-
and class- functions
functions  and
and  such that (3.3) holds. Furthermore, assume that there exists a continuous function
such that (3.3) holds. Furthermore, assume that there exists a continuous function  such that
such that  ,
,  , and
, and

where  is such that
is such that  . Finally, assume
. Finally, assume  exists. Then the nonlinear dynamical system (3.1), (3.2) is ultimately bounded with respect to
exists. Then the nonlinear dynamical system (3.1), (3.2) is ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound
with ultimate bound  where
where 
 . Furthermore,
. Furthermore,  . If, in addition,
. If, in addition,  and
and  is a class-
is a class- function, then the nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to
function, then the nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound
with ultimate bound  .
.
Proof.
See [20, page 787].
The following result on ultimate boundedness of interconnected systems is needed for the main theorems in this paper. For this result, recall the definition of input-to-state stability given in [21].
Proposition 3.4.
Consider the discrete-time nonlinear interconnected dynamical system (3.1) and (3.2). If (3.2) is input-to-state stable with  viewed as the input and (3.1) and (3.2) are ultimately bounded with respect to
viewed as the input and (3.1) and (3.2) are ultimately bounded with respect to  uniformly in
uniformly in  , then the solution
, then the solution  ,
,  , of the interconnected dynamical system (3.1)-(3.2), is ultimately bounded.
, of the interconnected dynamical system (3.1)-(3.2), is ultimately bounded.
Proof.
Since system (3.1)-(3.2) is ultimately bounded with respect to  (uniformly in
(uniformly in  ), there exist positive constants
), there exist positive constants  and
and  such that
such that  ,
,  . Furthermore, since (3.2) is input-to-state stable with
. Furthermore, since (3.2) is input-to-state stable with  viewed as the input, it follows that
viewed as the input, it follows that  is finite, and hence, there exist a class-
is finite, and hence, there exist a class- function
function  and a class-
and a class- function
function  such that
such that

which proves that the solution  ,
,  to (3.1) and (3.2) is ultimately bounded.
to (3.1) and (3.2) is ultimately bounded.
4. Neuroadaptive Control for Discrete-Time Nonlinear Nonnegative Uncertain Systems
In this section, we consider the problem of characterizing neuroadaptive feedback control laws for discrete-time nonlinear nonnegative and compartmental uncertain dynamical systems to achieve set-point regulation in the nonnegative orthant. Specifically, consider the controlled discrete-time nonlinear uncertain dynamical system  given by
given by


where  ,
,  , and
, and  ,
,  , are the state vectors,
, are the state vectors,  ,
,  , is the control input,
, is the control input,  is nonnegative with respect to
is nonnegative with respect to  but otherwise unknown and satisfies
but otherwise unknown and satisfies  ,
,  ,
,  is nonnegative with respect to
is nonnegative with respect to  but otherwise unknown and satisfies
but otherwise unknown and satisfies  ,
,  , and
, and  is a known nonnegative input matrix function. Here, we assume that we have
is a known nonnegative input matrix function. Here, we assume that we have  control inputs so that the input matrix function is given by
control inputs so that the input matrix function is given by

where  is a positive diagonal matrix and
is a positive diagonal matrix and  is a nonnegative matrix function such that
is a nonnegative matrix function such that  ,
,  . The control input
. The control input  in (4.1) is restricted to the class of admissible controls consisting of measurable functions such that
in (4.1) is restricted to the class of admissible controls consisting of measurable functions such that  ,
,  . In this section, we do not place any restriction on the sign of the control signal and design a neuroadaptive controller that guarantees that the system states remain in the nonnegative orthant of the state space for nonnegative initial conditions and are ultimately bounded in the neighborhood of a desired equilibrium point.
. In this section, we do not place any restriction on the sign of the control signal and design a neuroadaptive controller that guarantees that the system states remain in the nonnegative orthant of the state space for nonnegative initial conditions and are ultimately bounded in the neighborhood of a desired equilibrium point.
In this paper, we assume that  and
and  are unknown functions with
are unknown functions with  given by
given by

where  is a known nonnegative matrix and
is a known nonnegative matrix and  is an unknown nonnegative function with respect to
is an unknown nonnegative function with respect to  and belongs to the uncertainty set
and belongs to the uncertainty set  given by
given by

where  and
and  is an uncertain continuous function such that
is an uncertain continuous function such that  is nonnegative with respect to
is nonnegative with respect to  . Furthermore, we assume that for a given
. Furthermore, we assume that for a given  there exist
there exist  and
and  such that
such that


In addition, we assume that (4.2) is input-to-state stable at  with
with  viewed as the input, that is, there exist a class-
viewed as the input, that is, there exist a class- function
function  and a class-
and a class- function
function  such that
such that

where  denotes the Euclidean vector norm. Unless otherwise stated, henceforth we use
denotes the Euclidean vector norm. Unless otherwise stated, henceforth we use  to denote the Euclidean vector norm. Note that
to denote the Euclidean vector norm. Note that  is an equilibrium point of (4.1) and (4.2) if and only if there exists
is an equilibrium point of (4.1) and (4.2) if and only if there exists  such that (4.6) and (4.7) hold.
such that (4.6) and (4.7) hold.
Furthermore, we assume that, for a given  , the
, the  th component of the vector function
th component of the vector function  can be approximated over a compact set
can be approximated over a compact set  by a linear in the parameters neural network up to a desired accuracy so that for
by a linear in the parameters neural network up to a desired accuracy so that for  , there exists
, there exists  such that
such that  ,
,  , and
, and

where  ,
,  , are optimal unknown (constant) weights that minimize the approximation error over
, are optimal unknown (constant) weights that minimize the approximation error over  ,
,  ,
,  , are a set of basis functions such that each component of
, are a set of basis functions such that each component of  takes values between 0 and 1,
takes values between 0 and 1,  ,
,  , are the modeling errors, and
, are the modeling errors, and  , where
, where  ,
,  , are bounds for the optimal weights
, are bounds for the optimal weights  ,
,  .
.
Since  is continuous, we can choose
is continuous, we can choose  ,
,  , from a linear space
, from a linear space  of continuous functions that forms an algebra and separates points in
of continuous functions that forms an algebra and separates points in  . In this case, it follows from the Stone-Weierstrass theorem [22, page 212] that
. In this case, it follows from the Stone-Weierstrass theorem [22, page 212] that  is a dense subset of the set of continuous functions on
is a dense subset of the set of continuous functions on  . Now, as is the case in the standard neuroadaptive control literature [23], we can construct the signal
. Now, as is the case in the standard neuroadaptive control literature [23], we can construct the signal  involving the estimates of the optimal weights as our adaptive control signal. However, even though
involving the estimates of the optimal weights as our adaptive control signal. However, even though  ,
,  , provides adaptive cancellation of the system uncertainty, it does not necessarily guarantee that the state trajectory of the closed-loop system remains in the nonnegative orthant of the state space for nonnegative initial conditions.
, provides adaptive cancellation of the system uncertainty, it does not necessarily guarantee that the state trajectory of the closed-loop system remains in the nonnegative orthant of the state space for nonnegative initial conditions.
To ensure nonnegativity of the closed-loop plant states, the adaptive control signal is assumed to be of the form  ,
,  , where
, where  is such that each component of
is such that each component of  takes values between 0 and 1 and
takes values between 0 and 1 and  , whenever
, whenever  for all
for all  ,
,  , where
, where  and
and  are the
are the  th element of
th element of  and
and  , respectively. This set of functions do not generate an algebra in
, respectively. This set of functions do not generate an algebra in  , and hence, if used as an approximator for
, and hence, if used as an approximator for  ,
,  , will generate additional conservatism in the ultimate bound guarantees provided by the neural network controller. In particular, since each component of
, will generate additional conservatism in the ultimate bound guarantees provided by the neural network controller. In particular, since each component of  and
and  takes values between 0 and 1, it follows that
takes values between 0 and 1, it follows that

This upper bound is used in the proof of Theorem 4.1 below.
For the remainder of the paper we assume that there exists a gain matrix  such that
such that  is nonnegative and asymptotically stable, where
is nonnegative and asymptotically stable, where  and
and  have the forms of (2.6) and (2.5), respectively. Now, partitioning the state in (4.1) as
have the forms of (2.6) and (2.5), respectively. Now, partitioning the state in (4.1) as  , where
, where  and
and  , and using (4.3), it follows that (4.1) and (4.2) can be written as
, and using (4.3), it follows that (4.1) and (4.2) can be written as



Thus, since  is nonnegative and asymptotically stable, it follows from Theorem 2.4 that the solution
is nonnegative and asymptotically stable, it follows from Theorem 2.4 that the solution  of (4.12) with
of (4.12) with  , where
, where  and
and  satisfy
satisfy  , is globally exponentially stable, and hence, (4.12) is input-to-state stable at
, is globally exponentially stable, and hence, (4.12) is input-to-state stable at  with
with  viewed as the input. Thus, in this paper we assume that the dynamics (4.12) can be included in (4.2) so that
viewed as the input. Thus, in this paper we assume that the dynamics (4.12) can be included in (4.2) so that  . In this case, the input matrix (4.3) is given by
. In this case, the input matrix (4.3) is given by

so that  . Now, for a given desired set point
. Now, for a given desired set point  and for some
and for some  , our aim is to design a control input
, our aim is to design a control input  ,
,  , such that
, such that  and
and  for all
for all  , where
, where  , and
, and  and
and  ,
,  , for all
, for all  . However, since in many applications of nonnegative systems and, in particular, compartmental systems, it is often necessary to regulate a subset of the nonnegative state variables which usually include a central compartment, here we only require that
. However, since in many applications of nonnegative systems and, in particular, compartmental systems, it is often necessary to regulate a subset of the nonnegative state variables which usually include a central compartment, here we only require that  ,
,  .
.
Theorem 4.1.
Consider the discrete-time nonlinear uncertain dynamical system  given by (4.1) and (4.2) where
given by (4.1) and (4.2) where  and
and  are given by (4.4) and (4.14), respectively,
are given by (4.4) and (4.14), respectively,  is nonnegative with respect to
is nonnegative with respect to  ,
,  is nonnegative with respect to
is nonnegative with respect to  , and
, and  is nonnegative with respect to
is nonnegative with respect to  and belongs to
and belongs to  . For a given
. For a given  assume there exist nonnegative vectors
assume there exist nonnegative vectors  and
and  such that (4.6) and (4.7) hold. Furthermore, assume that (4.2) is input-to-state stable at
such that (4.6) and (4.7) hold. Furthermore, assume that (4.2) is input-to-state stable at  with
with  viewed as the input. Finally, let
viewed as the input. Finally, let  be such that
be such that  is nonnegative and
is nonnegative and  is nonnegative and asymptotically stable. Then the neuroadaptive feedback control law
is nonnegative and asymptotically stable. Then the neuroadaptive feedback control law

where

 ,
,  ,
,  , and
, and  with
with  whenever
whenever  ,
,  ,
,  ,—with update law
,—with update law

where  satisfies
satisfies

for positive definite  ,
,  and
and  are positive constants satisfying
are positive constants satisfying  and
and  ,
,  , and
, and  —guarantees that there exists a positively invariant set
—guarantees that there exists a positively invariant set  such that
such that  , where
, where  , and the solution
, and the solution  ,
,  , of the closed-loop system given by (4.1), (4.2), (4.15), and (4.17) is ultimately bounded for all
, of the closed-loop system given by (4.1), (4.2), (4.15), and (4.17) is ultimately bounded for all  with ultimate bound
with ultimate bound  ,
,  , where
, where


 ,
,  ,
,  ,
,  , and
, and  and
and  are positive constants satisfying
are positive constants satisfying  and
and  , respectively. Furthermore,
, respectively. Furthermore,  and
and  ,
,  , for all
, for all  .
.
Proof.
See Appendix A.
A block diagram showing the neuroadaptive control architecture given in Theorem 4.1 is shown in Figure 1. It is important to note that the adaptive control law (4.15) and (4.17) does not require the explicit knowledge of the optimal weighting matrix  and constants
and constants  and
and  . All that is required is the existence of the nonnegative vectors
. All that is required is the existence of the nonnegative vectors  and
and  such that the equilibrium conditions (4.6), and (4.7) hold. Furthermore, in the case where
such that the equilibrium conditions (4.6), and (4.7) hold. Furthermore, in the case where  is an unknown positive diagonal matrix but
is an unknown positive diagonal matrix but  ,
,  , where
, where  is known, we can take the gain matrix
is known, we can take the gain matrix  to be diagonal so that
to be diagonal so that  , where
, where  is such that
is such that  ,
,  . In this case, taking
. In this case, taking  in (4.4) to be the identity matrix,
in (4.4) to be the identity matrix,  is given by
is given by  which is clearly nonnegative and asymptotically stable, and hence, any positive diagonal matrix
which is clearly nonnegative and asymptotically stable, and hence, any positive diagonal matrix  satisfies (4.18). Finally, it is important to note that the control input signal
satisfies (4.18). Finally, it is important to note that the control input signal  ,
,  , in Theorem 4.1 can be negative depending on the values of
, in Theorem 4.1 can be negative depending on the values of  ,
,  . However, as is required for nonnegative and compartmental dynamical systems the closed-loop plant states remain nonnegative.
. However, as is required for nonnegative and compartmental dynamical systems the closed-loop plant states remain nonnegative.
Next, we generalize Theorem 4.1 to the case where the input matrix is not necessarily nonnegative. For this result  denotes the
denotes the  th row of
th row of  .
.
Theorem 4.2.
Consider the discrete-time nonlinear uncertain dynamical system  given by (4.1) and (4.2), where
given by (4.1) and (4.2), where  and
and  are given by (4.4) and (4.14), respectively,
are given by (4.4) and (4.14), respectively,  is nonnegative with respect to
is nonnegative with respect to  ,
,  is nonnegative with respect to
is nonnegative with respect to  , and
, and  is nonnegative with respect to
is nonnegative with respect to  and belongs to
and belongs to  . For a given
. For a given  , assume there exist a nonnegative vector
, assume there exist a nonnegative vector  and a vector
and a vector  such that (4.6) and (4.7) hold with
such that (4.6) and (4.7) hold with  . Furthermore, assume that (4.2) is input-to-state stable at
. Furthermore, assume that (4.2) is input-to-state stable at  with
with  viewed as the input. Finally, let
viewed as the input. Finally, let  be such that
be such that  ,
,  , and
, and  is nonnegative and asymptotically stable. Then the neuroadaptive feedback control law (4.15), where
is nonnegative and asymptotically stable. Then the neuroadaptive feedback control law (4.15), where  is given by (4.16) with
is given by (4.16) with  ,
,  ,
,  , and
, and  with
with  whenever
whenever  ,
,  ,
,  ,—with update law
,—with update law

where  satisfies (4.18),
satisfies (4.18),  and
and  are positive constants satisfying
are positive constants satisfying  and
and  ,
,  ,
,  —guarantees that there exists a positively invariant set
—guarantees that there exists a positively invariant set  such that
such that  , where
, where  , and the solution
, and the solution  ,
,  , of the closed-loop system given by (4.1), (4.2), (4.15), and (4.21) is ultimately bounded for all
, of the closed-loop system given by (4.1), (4.2), (4.15), and (4.21) is ultimately bounded for all  with ultimate bound
with ultimate bound  ,
,  , where
, where  is given by (4.19) with
is given by (4.19) with  replaced by
replaced by  in
in  and
and  ,
,  . Furthermore,
. Furthermore,  and
and  ,
,  , for all
, for all  .
.
Proof.
The proof is identical to the proof of Theorem 4.1 with  replaced by
replaced by  .
.
Finally, in the case where  is an unknown diagonal matrix but the sign of each diagonal element is known and
is an unknown diagonal matrix but the sign of each diagonal element is known and  ,
,  , where
, where  is known, we can take the gain matrix
is known, we can take the gain matrix  to be diagonal so that
to be diagonal so that  , where
, where  is such that
is such that  ,
,  . In this case, taking
. In this case, taking  in (4.4) to be the identity matrix,
in (4.4) to be the identity matrix,  is given by
is given by  which is nonnegative and asymptotically stable.
which is nonnegative and asymptotically stable.
Example 4.3.
Consider the nonlinear uncertain system (4.1) with

where  are unknown. For simplicity of exposition, here we assume that there is no internal dynamics. Note that
are unknown. For simplicity of exposition, here we assume that there is no internal dynamics. Note that  and
and  in (4.22) can be written in the form of (4.4) and (4.3) with
in (4.22) can be written in the form of (4.4) and (4.3) with  ,
,  ,
,  , and
, and  . Furthermore, note that
. Furthermore, note that  is unknown and belongs to
is unknown and belongs to  . Since for
. Since for  there exists
there exists  such that (4.6) is satisfied, it follows from Theorem 4.2 that the neuroadaptive feedback control law (4.15) with
such that (4.6) is satisfied, it follows from Theorem 4.2 that the neuroadaptive feedback control law (4.15) with  and update law (4.21) guarantees that the closed-loop systems trajectory is ultimately bounded and remains in the nonnegative orthant of the state space for nonnegative initial conditions. With
and update law (4.21) guarantees that the closed-loop systems trajectory is ultimately bounded and remains in the nonnegative orthant of the state space for nonnegative initial conditions. With  ,
,  ,
,  ,
,  ,
,  ,
,  , and initial conditions
, and initial conditions  and
and  , Figure 2 shows the state trajectories versus time and the control signal versus time.
, Figure 2 shows the state trajectories versus time and the control signal versus time.
5. Neuroadaptive Control for Discrete-Time Nonlinear Nonnegative Uncertain Systems with Nonnegative Control
As discussed in the introduction, control (source) inputs of drug delivery systems for physiological and pharmacological processes are usually constrained to be nonnegative as are the system states. Hence, in this section we develop neuroadaptive control laws for discrete-time nonnegative systems with nonnegative control inputs. In general, unlike linear nonnegative systems with asymptotically stable plant dynamics, a given set point  for a discrete-time nonlinear nonnegative dynamical system
for a discrete-time nonlinear nonnegative dynamical system

where  ,
,  , and
, and  , may not be asymptotically stabilizable with a constant control
, may not be asymptotically stabilizable with a constant control  . Hence, we assume that the set point
. Hence, we assume that the set point  satisfying
satisfying  is a unique equilibrium point in the nonnegative orthant with
is a unique equilibrium point in the nonnegative orthant with  and is also asymptotically stable for all
and is also asymptotically stable for all  . This implies that the equilibrium solution
. This implies that the equilibrium solution  to (5.1) with
to (5.1) with  is asymptotically stable for all
is asymptotically stable for all  .
.
In this section, we assume that  in (4.4) is nonnegative and asymptotically stable, and hence, without loss of generality (see [19, Proposition 3.1]), we can assume that
in (4.4) is nonnegative and asymptotically stable, and hence, without loss of generality (see [19, Proposition 3.1]), we can assume that  is an asymptotically stable compartmental matrix [19]. Furthermore, we assume that the control inputs are injected directly into
is an asymptotically stable compartmental matrix [19]. Furthermore, we assume that the control inputs are injected directly into  separate compartments so that
separate compartments so that  and
and  in (4.14) are such that
in (4.14) are such that  is a positive diagonal matrix and
is a positive diagonal matrix and  , where
, where  ,
,  , is a known positive diagonal matrix function. For compartmental systems, this assumption is not restrictive since control inputs correspond to control inflows to each individual compartment. For the statement of the next theorem, recall the definitions of
, is a known positive diagonal matrix function. For compartmental systems, this assumption is not restrictive since control inputs correspond to control inflows to each individual compartment. For the statement of the next theorem, recall the definitions of  and
and  ,
,  , given in Theorem 4.1.
, given in Theorem 4.1.
Theorem 5.1.
Consider the discrete-time nonlinear uncertain dynamical system  given by (4.1) and (4.2), where
given by (4.1) and (4.2), where  and
and  are given by (4.4) and (4.14), respectively,
are given by (4.4) and (4.14), respectively,  is nonnegative and asymptotically stable,
is nonnegative and asymptotically stable,  is nonnegative with respect to
is nonnegative with respect to  ,
,  is nonnegative with respect to
is nonnegative with respect to  , and
, and  is nonnegative with respect to
is nonnegative with respect to  and belongs to
and belongs to  . For a given
. For a given  assume there exist positive vectors
assume there exist positive vectors  and
and  such that (4.6) and (4.7) hold and the set point
such that (4.6) and (4.7) hold and the set point  is asymptotically stable with constant control
is asymptotically stable with constant control  for all
for all  . In addition, assume that (4.2) is input-to-state stable at
. In addition, assume that (4.2) is input-to-state stable at  with
with  viewed as the input. Then the neuroadaptive feedback control law
viewed as the input. Then the neuroadaptive feedback control law

where

and  ,
,  ,
,  ,—with update law
,—with update law

where  satisfies
satisfies

for positive definite  ,
,  and
and  are positive constants satisfying
are positive constants satisfying  and
and  ,
,  ,
,  —guarantees that there exists a positively invariant set
—guarantees that there exists a positively invariant set  such that
such that  and the solution
and the solution  ,
,  , of the closed-loop system given by (4.1), (4.2), (5.2), and (5.4) is ultimately bounded for all
, of the closed-loop system given by (4.1), (4.2), (5.2), and (5.4) is ultimately bounded for all  with ultimate bound
with ultimate bound  ,
,  , where
, where  ,
,

 ,
,  ,
,  ,
,  , and
, and  and
and  are positive constants satisfying
are positive constants satisfying  and
and  . Furthermore,
. Furthermore,  ,
,  , and
, and  ,
,  , for all
, for all  .
.
Proof.
See Appendix B.
6. Conclusion
In this paper, we developed a neuroadaptive control framework for adaptive set-point regulation of discrete-time nonlinear uncertain nonnegative and compartmental systems. Using Lyapunov methods, the proposed framework was shown to guarantee ultimate boundedness of the error signals corresponding to the physical system states and the neural network weighting gains while additionally guaranteeing the nonnegativity of the closed-loop system states associated with the plant dynamics.
References
Hayakawa T, Haddad WM, Bailey JM, Hovakimyan N: Passivity-based neural network adaptive output feedback control for nonlinear nonnegative dynamical systems. IEEE Transactions on Neural Networks 2005, 16(2):387-398. 10.1109/TNN.2004.841782
Hayakawa T, Haddad WM, Hovakimyan N, Chellaboina V: Neural network adaptive control for nonlinear nonnegative dynamical systems. IEEE Transactions on Neural Networks 2005, 16(2):399-413. 10.1109/TNN.2004.841791
Berman A, Plemmons RJ: Nonnegative Matrices in the Mathematical Sciences. Academic Press, New York, NY, USA; 1979:xviii+316.
Berman A, Neumann M, Stern RJ: Nonnegative Matrices in Dynamic Systems, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 1989:xxii+167.
Farina L, Rinaldi S: Positive Linear Systems: Theory and Application, Pure and Applied Mathematics. John Wiley & Sons, New York, NY, USA; 2000:x+305.
Kaszkurewicz E, Bhaya A: Matrix Diagonal Stability in Systems and Computation. Birkhäuser, Boston, Mass, USA; 2000:xiv+267.
Kaczorek T: Positive 1D and 2D Systems. Springer, London, UK; 2002.
Haddad WM, Chellaboina V: Stability and dissipativity theory for nonnegative dynamical systems: a unified analysis framework for biological and physiological systems. Nonlinear Analysis: Real World Applications 2005, 6(1):35-65. 10.1016/j.nonrwa.2004.01.006
Mohler RR: Biological modeling with variable compartmental structure. IEEE Transactions on Automatic Control 1974, 19(6):922-926. 10.1109/TAC.1974.1100739
Maeda H, Kodama S, Kajiya F: Compartmental system analysis: realization of a class of linear systems with physical constraints. IEEE Transactions on Circuits and Systems 1977, 24(1):8-14. 10.1109/TCS.1977.1084267
Sandberg IW: On the mathematical foundations of compartmental analysis in biology, medicine, and ecology. IEEE Transactions on Circuits and Systems 1978, 25(5):273-279. 10.1109/TCS.1978.1084473
Maeda H, Kodama S, Ohta Y: Asymptotic behavior of nonlinear compartmental systems: nonoscillation and stability. IEEE Transactions on Circuits and Systems 1978, 25(6):372-378. 10.1109/TCS.1978.1084490
Funderlic RE, Mankin JB: Solution of homogeneous systems of linear equations arising from compartmental models. SIAM Journal on Scientific and Statistical Computing 1981, 2(4):375-383. 10.1137/0902030
Anderson DH: Compartmental Modeling and Tracer Kinetics, Lecture Notes in Biomathematics. Volume 50. Springer, Berlin, Germany; 1983:vii+302.
Godfrey K: Compartmental Models and Their Application. Academic Press, London, UK; 1983:xiv+293.
Jacquez JA: Compartmental Analysis in Biology and Medicine. University of Michigan Press, Ann Arbor, Mich, USA; 1985.
Bernstein DS, Hyland DC: Compartmental modeling and second-moment analysis of state space systems. SIAM Journal on Matrix Analysis and Applications 1993, 14(3):880-901. 10.1137/0614060
Jacquez JA, Simon CP: Qualitative theory of compartmental systems. SIAM Review 1993, 35(1):43-79. 10.1137/1035003
Haddad WM, Chellaboina V, August E: Stability and dissipativity theory for discrete-time non-negative and compartmental dynamical systems. International Journal of Control 2003, 76(18):1845-1861. 10.1080/00207170310001635400
Haddad WM, Chellaboina V: Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach. Princeton University Press, Princeton, NJ, USA; 2008.
Jiang Z-P, Wang Y: Input-to-state stability for discrete-time nonlinear systems. Automatica 2001, 37(6):857-869. 10.1016/S0005-1098(01)00028-0
Royden HL: Real Analysis. 3rd edition. Macmillan, New York, NY, USA; 1988:xx+444.
Lewis FL, Jagannathan S, Yesildirak A: Neural Network Control of Robot Manipulators and Nonlinear Systems. Taylor & Francis, London, UK; 1999.
Acknowledgments
This research was supported in part by the Air Force Office of Scientific Research under Grant no. FA9550-06-1-0240 and the National Science Foundation under Grant no. ECS-0601311.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Proof of Theorem 4.1
In this appendix, we prove Theorem 4.1. First, note that with  ,
,  , given by (4.15), it follows from (4.1), (4.4), and (4.14) that
, given by (4.15), it follows from (4.1), (4.4), and (4.14) that


Now, defining  and
and  , using (4.5)–(4.7), (4.9), and
, using (4.5)–(4.7), (4.9), and  , it follows from (4.2) and (A.1) that
, it follows from (4.2) and (A.1) that




where  ,
,  ,
,  ,
,  ,
,  , and
, and  . Furthermore, since
. Furthermore, since  is nonnegative and asymptotically stable, it follows from Theorem 2.3 that there exist a positive diagonal matrix
is nonnegative and asymptotically stable, it follows from Theorem 2.3 that there exist a positive diagonal matrix  and a positive-definite matrix
and a positive-definite matrix  such that (4.18) holds.
such that (4.18) holds.
Next, to show that the closed-loop system given by (4.17), (A.2), and (A.3) is ultimately bounded with respect to  , consider the Lyapunov-like function
, consider the Lyapunov-like function


where  . Note that (A.4) satisfies (3.3) with
. Note that (A.4) satisfies (3.3) with  ,
,  ,
,  , where
, where  . Furthermore,
. Furthermore,  is a class-
is a class- function. Now, using (4.17) and (A.2), it follows that the difference of
function. Now, using (4.17) and (A.2), it follows that the difference of  along the closed-loop system trajectories is given by
along the closed-loop system trajectories is given by


Next, using








it follows that


Furthermore, note that since, by assumption,  and
and  ,
,  , it follows that
, it follows that


Hence,


Now, for


it follows that  for all
for all  , that is,
, that is,  for all
for all  and
and  , where
, where


Furthermore, it follows from (A.12) that


Hence, it follows from (A.4) and (A.15) that


where  . Thus, it follows from Theorem 3.2 that the closed-loop system given by (4.17), (A.2), and (A.3) is globally bounded with respect to
. Thus, it follows from Theorem 3.2 that the closed-loop system given by (4.17), (A.2), and (A.3) is globally bounded with respect to  uniformly in
uniformly in  , and for every
, and for every  ,
,  ,
,  , where
, where


 , and
, and  . Furthermore, to show that
. Furthermore, to show that  ,
,  , suppose there exists
, suppose there exists  such that
such that  for all
for all  . In this case,
. In this case,  ,
,  , which implies
, which implies  ,
,  . Alternatively, suppose there does not exist
. Alternatively, suppose there does not exist  such that
such that  for all
for all  . In this case, there exists an infinite set
. In this case, there exists an infinite set  . Now, with (A.13) satisfied, it follows that
. Now, with (A.13) satisfied, it follows that  for all
for all  , that is,
, that is,  for all
for all  and
and  , where
, where  is given by (A.14). Furthermore, note that
is given by (A.14). Furthermore, note that  ,
,  , and (A.16) holds. Hence, it follows from Theorem 3.3 that the closed-loop system given by (4.17), (A.2), and (A.3) is globally ultimately bounded with respect to
, and (A.16) holds. Hence, it follows from Theorem 3.3 that the closed-loop system given by (4.17), (A.2), and (A.3) is globally ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound given by
with ultimate bound given by  , where
, where  .
.
Next, to show ultimate boundedness of the error dynamics, consider the Lyapunov-like function


Note that (A.18) satisfies


with  ,
,  ,
,  ,
,  , and
, and  , where
, where  . Furthermore,
. Furthermore,  is a class-
is a class- function. Now, using (4.18), (A.10), and the definition of
function. Now, using (4.18), (A.10), and the definition of  , it follows that the difference of
, it follows that the difference of  along the closed-loop system trajectories is given by
along the closed-loop system trajectories is given by


where in (A.20) we used  and
and  for
for  and
and  . Now, noting
. Now, noting  and
and  , using the inequalities
, using the inequalities


and rearranging terms in (A.20) yields


Now, for


it follows that  for all
for all  , where
, where


or, equivalently,  for all
for all  ,
,  , where (see Figure 3)
, where (see Figure 3)




Next, we show that  ,
,  . Since
. Since  for all
for all  , it follows that, for
, it follows that, for  ,
,  ,
,


Now, let  and assume
and assume  . If
. If  ,
,  , then it follows that
, then it follows that  ,
,  . Alternatively, if there exists
. Alternatively, if there exists  such that
such that  , then, since
, then, since  , it follows that there exists
, it follows that there exists  , such that
, such that  and
and  , where
, where  . Hence, it follows that
. Hence, it follows that


which implies that  . Next, let
. Next, let  , where
, where  and assume
and assume  and
and  . Now, for every
. Now, for every  such that
such that  ,
,  , it follows that
, it follows that


which implies that  ,
,  . Now, if there exists
. Now, if there exists  such that
such that  , then it follows as in the earlier case shown above that
, then it follows as in the earlier case shown above that  ,
,  . Hence, if
. Hence, if  , then
, then


Finally, repeating the above arguments with  ,
,  , replaced by
, replaced by  ,
,  , it can be shown that
, it can be shown that  ,
,  , where
, where  .
.
Figure 3
Visualization of sets used in the proof of Theorem 4. 1.
Next, define


where  is the maximum value such that
is the maximum value such that  , and define
, and define


where  is given by (A.30). Assume that
is given by (A.30). Assume that  (see Figure 3) (this assumption is standard in the neural network literature and ensures that in the error space
(see Figure 3) (this assumption is standard in the neural network literature and ensures that in the error space  there exists at least one Lyapunov level set
there exists at least one Lyapunov level set  . In the case where the neural network approximation holds in
. In the case where the neural network approximation holds in  , this assumption is automatically satisfied. See Remark A.1 for further details). Now, for all
, this assumption is automatically satisfied. See Remark A.1 for further details). Now, for all  ,
,  . Alternatively, for all
. Alternatively, for all  ,
,  . Hence, it follows that
. Hence, it follows that  is positively invariant. In addition, since (A.3) is input-to-state stable with
is positively invariant. In addition, since (A.3) is input-to-state stable with  viewed as the input, it follows from Proposition 3.4 that the solution
viewed as the input, it follows from Proposition 3.4 that the solution  ,
,  , to (A.3) is ultimately bounded. Furthermore, it follows from [21, Theorem 1] that there exist a continuous, radially unbounded, positive-definite function
, to (A.3) is ultimately bounded. Furthermore, it follows from [21, Theorem 1] that there exist a continuous, radially unbounded, positive-definite function  , a class-
, a class- function
function  , and a class-
, and a class- function
function  such that
such that


Since the upper bound for  is given by
is given by  , it follows that the set given by
, it follows that the set given by


is also positively invariant as long as  (see Remark A.1). Now, since
(see Remark A.1). Now, since  and
and  are positively invariant, it follows that
are positively invariant, it follows that


is also positively invariant. In addition, since (4.1), (4.2), (4.15), and (4.17) are ultimately bounded with respect to  and since (4.2) is input-to-state stable at
and since (4.2) is input-to-state stable at  with
with  viewed as the input then it follows from Proposition 3.4 that the solution
viewed as the input then it follows from Proposition 3.4 that the solution  ,
,  , of the closed-loop system (4.1), (4.2), (4.15), and (4.17) is ultimately bounded for all
, of the closed-loop system (4.1), (4.2), (4.15), and (4.17) is ultimately bounded for all  .
.
Finally, to show that  and
and  ,
,  , for all
, for all  note that the closed-loop system (4.1), (4.15), and (4.17), is given by
note that the closed-loop system (4.1), (4.15), and (4.17), is given by


where


Note that  and
and  are nonnegative and, since
are nonnegative and, since  whenever
whenever  ,
,  ,
,  ,
,  . Hence, since
. Hence, since  is nonnegative with respect to
is nonnegative with respect to  pointwise-in-time,
pointwise-in-time,  is nonnegative with respect to
is nonnegative with respect to  , and
, and  , it follows from Proposition 2.9 that
, it follows from Proposition 2.9 that  ,
,  , and
, and  ,
,  , for all
, for all  .
.
Remark A.1.
In the case where the neural network approximation holds in  , the assumptions
, the assumptions  and
and  invoked in the proof of Theorem 4.1 are automatically satisfied. Furthermore, in this case the control law (4.15) ensures global ultimate boundedness of the error signals. However, the existence of a global neural network approximator for an uncertain nonlinear map cannot in general be established. Hence, as is common in the neural network literature, for a given arbitrarily large compact set
invoked in the proof of Theorem 4.1 are automatically satisfied. Furthermore, in this case the control law (4.15) ensures global ultimate boundedness of the error signals. However, the existence of a global neural network approximator for an uncertain nonlinear map cannot in general be established. Hence, as is common in the neural network literature, for a given arbitrarily large compact set  , we assume that there exists an approximator for the unknown nonlinear map up to a desired accuracy. Furthermore, we assume that in the error space
, we assume that there exists an approximator for the unknown nonlinear map up to a desired accuracy. Furthermore, we assume that in the error space  there exists at least one Lyapunov level set such that
there exists at least one Lyapunov level set such that  . In the case where
. In the case where  is continuous on
is continuous on  , it follows from the Stone-Weierstrass theorem that
, it follows from the Stone-Weierstrass theorem that  can be approximated over an arbitrarily large compact set
can be approximated over an arbitrarily large compact set  . In this case, our neuroadaptive controller guarantees semiglobal ultimate boundedness. An identical assumption is made in the proof of Theorem 5.1.
. In this case, our neuroadaptive controller guarantees semiglobal ultimate boundedness. An identical assumption is made in the proof of Theorem 5.1.
B. Proof of Theorem 5.1
In this appendix, we prove Theorem 5.1. First, define  , where
, where


Next, note that with  ,
,  , given by (5.2), it follows from (4.1), (4.4), and (4.14) that
, given by (5.2), it follows from (4.1), (4.4), and (4.14) that


Now, defining  and
and  and using (4.6), (4.7), and 4.9), it follows from (4.2) and (B.2) that
and using (4.6), (4.7), and 4.9), it follows from (4.2) and (B.2) that




where  , and
, and  . Furthermore, since
. Furthermore, since  is nonnegative and asymptotically stable, it follows from Theorem 2.3 that there exist a positive diagonal matrix
is nonnegative and asymptotically stable, it follows from Theorem 2.3 that there exist a positive diagonal matrix  and a positive-definite matrix
and a positive-definite matrix  such that (5.5) holds.
such that (5.5) holds.
Next, to show ultimate boundedness of the closed-loop system (5.4), (B.3), and (B.4), consider the Lyapunov-like function


where  and
and  with
with  . Note that (B.5) satisfies (3.3) with
. Note that (B.5) satisfies (3.3) with  ,
,  ,
,  , where
, where  . Furthermore,
. Furthermore,  is a class-
is a class- function. Now, using (5.4) and (B.3), it follows that the difference of
function. Now, using (5.4) and (B.3), it follows that the difference of  along the closed-loop system trajectories is given by
along the closed-loop system trajectories is given by


Now, for each  and for the two cases given in (B.1), the right-hand side of (B.6) gives the following:
and for the two cases given in (B.1), the right-hand side of (B.6) gives the following:
-
(1)
if
 , then
, then  . Now, using (A.8), (A.9), and the inequalities
. Now, using (A.8), (A.9), and the inequalities (B.7)
(B.7) (B.8)
(B.8)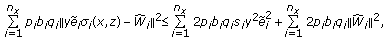 (B.9)
(B.9) (B.10)
(B.10)it follows that
 (B.11)
(B.11) -
(2)
otherwise,
 , and hence, using (A.8), (A.9), (B.7), (B.9), and (B.10), it follows that
, and hence, using (A.8), (A.9), (B.7), (B.9), and (B.10), it follows that (B.12)
(B.12)
Hence, it follows from (B.6) that in either case


Furthermore, note that since, by assumption,  and
and  ,
,  ,
,  , it follows that
, it follows that


Hence,


Now, it follows using similar arguments as in the proof of Theorem 4.1 that the closed-loop system (5.4), (B.3), and (B.4) is globally bounded with respect to  uniformly in
uniformly in  . If there does not exist
. If there does not exist  such that
such that  for all
for all  , it follows using similar arguments as in the proof of Theorem 4.1 that the closed-loop system (5.4), (B.3), and (B.4) is globally ultimately bounded with respect to
, it follows using similar arguments as in the proof of Theorem 4.1 that the closed-loop system (5.4), (B.3), and (B.4) is globally ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound given by
with ultimate bound given by  , where
, where  . Alternatively, if there exists
. Alternatively, if there exists  such that
such that  for all
for all  , then
, then  for all
for all  .
.
Next, to show ultimate boundedness of the error dynamics, consider the Lyapunov-like function


Note that (B.16) satisfies (A.19) with  ,
,  ,
,  ,
,  , and
, and  , where
, where  Furthermore,
Furthermore,  is a class-
is a class- function. Now, using (5.5), (B.13), and the definition of
function. Now, using (5.5), (B.13), and the definition of  , it follows that the forward difference of
, it follows that the forward difference of  along the closed-loop system trajectories is given by
along the closed-loop system trajectories is given by


where once again in (B.17) we used  and
and  for
for  and
and  .
.
Next, using (A.21) and (B.17) yields


Now, using similar arguments as in the proof of Theorem 4.1 it follows that the solution  , of the closed-loop system (5.4), (B.3), and (B.4) is ultimately bounded for all
, of the closed-loop system (5.4), (B.3), and (B.4) is ultimately bounded for all  given by (A.35) and
given by (A.35) and  for
for  .
.
Finally,  , is a restatement of (5.2). Now, since
, is a restatement of (5.2). Now, since  , and
, and  , it follows from Proposition 2.8 that
, it follows from Proposition 2.8 that  and
and  , for all
, for all  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Haddad, W.M., Chellaboina, V., Hui, Q. et al. Neural Network Adaptive Control for Discrete-Time Nonlinear Nonnegative Dynamical Systems. Adv Differ Equ 2008, 868425 (2008). https://doi.org/10.1155/2008/868425
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/868425
 uniformly in
uniformly in if there exists
if there exists  such that, for every
such that, for every  , there exists
, there exists  such that
such that  implies
implies 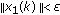 for all
for all  . The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to
. The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally bounded with respect to uniformly in
uniformly in if, for every
if, for every  , there exists
, there exists 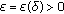 such that
such that  implies
implies  for all
for all  .
. uniformly in
uniformly in  with ultimate bound
with ultimate bound  if there exists
if there exists 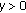 such that, for every
such that, for every 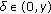 , there exists
, there exists 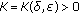 such that
such that  implies
implies  ,
,  . The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to
. The discrete-time nonlinear dynamical system (3.1) and (3.2) is globally ultimately bounded with respect to  uniformly in
uniformly in  with ultimate bound
with ultimate bound  if, for every
if, for every 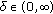 , there exists
, there exists 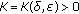 such that
such that  implies
implies 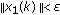 ,
, 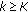 .
.

 , then
, then  . Now, using (A.8), (A.9), and the inequalities
. Now, using (A.8), (A.9), and the inequalities

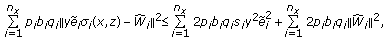


 , and hence, using (A.8), (A.9), (B.7), (B.9), and (B.10), it follows that
, and hence, using (A.8), (A.9), (B.7), (B.9), and (B.10), it follows that