- Research Article
- Open access
- Published:
Eigenvalue Problems for  -Laplacian Functional Dynamic Equations on Time Scales
-Laplacian Functional Dynamic Equations on Time Scales
Advances in Difference Equations volume 2008, Article number: 879140 (2008)
Abstract
This paper is concerned with the existence and nonexistence of positive solutions of the  -Laplacian functional dynamic equation on a time scale,
-Laplacian functional dynamic equation on a time scale,  ,
,  ,
,  ,
,  ,
,  ,
,  . We show that there exists a
. We show that there exists a  such that the above boundary value problem has at least two, one, and no positive solutions for
such that the above boundary value problem has at least two, one, and no positive solutions for  and
and  , respectively.
, respectively.
1. Introduction
Let  be a closed nonempty subset of
be a closed nonempty subset of  , and let
, and let  have the subspace topology inherited from the Euclidean topology on
have the subspace topology inherited from the Euclidean topology on  . In some of the current literature,
. In some of the current literature,  is called a time scale (please see [1, 2]). For notation, we will use the convention that, for each interval
is called a time scale (please see [1, 2]). For notation, we will use the convention that, for each interval  of
of  will denote time-scale interval, that is,
will denote time-scale interval, that is, 
In this paper, let  be a time scale such that
be a time scale such that  We are concerned with the existence of positive solutions of the
We are concerned with the existence of positive solutions of the  -Laplacian dynamic equation on a time scale
-Laplacian dynamic equation on a time scale

where  is the
is the  -Laplacian operator, that is,
-Laplacian operator, that is,  , where
, where  .
.
-
(H1)
The function
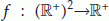 is continuous and nondecreasing about each element;
is continuous and nondecreasing about each element; 
-
(H2)
The function
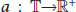 is left dense continuous (i.e.,
is left dense continuous (i.e., 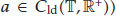 and does not vanish identically on any closed subinterval of
and does not vanish identically on any closed subinterval of  . Here
. Here  denotes the set of all left dense continuous functions from
denotes the set of all left dense continuous functions from 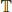 to
to  .
. -
(H3)
 is continuous and
is continuous and 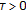 .
. -
(H4)
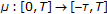 is continuous,
is continuous, 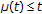 for all
for all 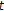 .
. -
(H5)
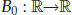 is continuous and nondecreasing;
is continuous and nondecreasing; 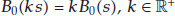 and satisfies that there exist
and satisfies that there exist 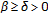 such that
such that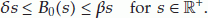 (1.2)
(1.2) -
(H6)
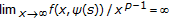 uniformly in
uniformly in 
 -Laplacian problems with two-, three-,
-Laplacian problems with two-, three-,  -point boundary conditions for ordinary differential equations and finite difference equations have been studied extensively, for example, see [1–4] and references therein. However, there are not many concerning the
-point boundary conditions for ordinary differential equations and finite difference equations have been studied extensively, for example, see [1–4] and references therein. However, there are not many concerning the  -Laplacian problems on time scales, especially for
-Laplacian problems on time scales, especially for  -Laplacian functional dynamic equations on time scales.
-Laplacian functional dynamic equations on time scales.
The motivations for the present work stems from many recent investigations in [5–10] and references therein. Especially, Kaufmann and Raffoul [7] considered a nonlinear functional dynamic equation on a time scale and obtained sufficient conditions for the existence of positive solutions, Li and Liu [10] studied the eigenvalue problem for second-order nonlinear dynamic equations on time scales. In this paper, our results show that the number of positive solutions of (1.1) is determined by the parameter  . That is to say, we prove that there exists a
. That is to say, we prove that there exists a  such that (1.1) has at least two, one, and no positive solutions for
such that (1.1) has at least two, one, and no positive solutions for  and
and  respectively.
respectively.
For convenience, we list the following well-known definitions which can be found in [11–13] and the references therein.
Definition 1.1.
For  and
and  , define the forward jump operator
, define the forward jump operator  and the backward jump operator
and the backward jump operator  , respectively, as
, respectively, as

If  is said to be right scattered, and if
is said to be right scattered, and if  is said to be left scattered. If
is said to be left scattered. If  is said to be right dense, and if
is said to be right dense, and if  is said to be left dense. If
is said to be left dense. If  has a right-scattered minimum
has a right-scattered minimum  define
define  otherwise set
otherwise set  If
If  has a left-scattered maximum
has a left-scattered maximum  define
define  otherwise set
otherwise set 
Definition 1.2.
For  and
and  define the deltaderivative of
define the deltaderivative of  to be the number (when it exists), with the property that, for any
to be the number (when it exists), with the property that, for any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

For  and
and  define the nabla derivative of
define the nabla derivative of  to be the number (when it exists), with the property that, for any
to be the number (when it exists), with the property that, for any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

If  , then
, then  If
If  , then
, then  is forward difference operator while
is forward difference operator while  is the backward difference operator.
is the backward difference operator.
Definition 1.3.
If  , then define the delta integral by
, then define the delta integral by  If
If  , then define the nabla integral by
, then define the nabla integral by 
The following lemma is crucial to prove our main results.
Lemma 1.4 ([14]).
Let  be a Banach space and let
be a Banach space and let  be a cone in
be a cone in  . For
. For  , define
, define  Assume that
Assume that  is completely continuous such that
is completely continuous such that  for
for 
-
(i)
If
 for
for 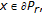 then
then 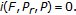
-
(ii)
If
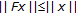 for
for  then
then 
2. Positive Solutions
We note that  is a solution of (1.1) if and only if
is a solution of (1.1) if and only if

Let  be endowed with the norm
be endowed with the norm  and define the cone of
and define the cone of  by
by

Clearly,  is a Banach space with the norm
is a Banach space with the norm  . For each
. For each  , extend
, extend  to
to  with
with  for
for  .
.
Define  as
as

We seek a fixed point,  , of
, of  in the cone
in the cone  . Define
. Define

Then  denotes a positive solution of BVP (1.1).
denotes a positive solution of BVP (1.1).
It follows from (2.3) that the following lemma holds.
Lemma 2.1.
Let  be defined by (2.3). If
be defined by (2.3). If  , then
, then
-
(i)
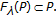
-
(ii)
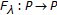 is completely continuous.
is completely continuous.
The proof of Lemma 2.1 can be found in [15].
We need to define further subsets of  with respect to the delay
with respect to the delay  . Set
. Set

Throughout this paper, we assume  and
and 
Lemma 2.2.
Suppose that (H1)–(H5) hold. Then there exists a  such that the operator
such that the operator  has a fixed point
has a fixed point  at
at  , where
, where  is the zero element of the Banach space
is the zero element of the Banach space  .
.
Proof.
Set

We know that  Let
Let  where
where

From above, we have

Let  and
and  Then
Then

By the Lebesgue dominated convergence theorem [16] together with (H3), it follows that  decreases to a fixed point
decreases to a fixed point  of the operator
of the operator  The proof is complete.
The proof is complete.
Lemma 2.3.
Suppose that (H1)–(H6) hold and that  for some
for some  . Then there exists a constant
. Then there exists a constant  such that for all
such that for all  and all possible fixed points
and all possible fixed points  of
of  at
at  , one has
, one has 
Proof.
Set

We need to prove that there exists a constant  such that
such that  for all
for all  If the number of elements of
If the number of elements of  is finite, then the result is obvious. If not, without loss of generality, we assume that there exists a sequence
is finite, then the result is obvious. If not, without loss of generality, we assume that there exists a sequence  such that
such that  , where
, where  is the fixed point of the operator
is the fixed point of the operator  defined by (2.3) at
defined by (2.3) at 
Then

We choose  such that
such that

 such that
such that

In view of (H6) there exists an  sufficiently large such that
sufficiently large such that  For
For  we have
we have

which is a contradiction. The proof is complete.
Lemma 2.4.
Suppose that (H1)–(H5) hold and that the operator  has a positive fixed point
has a positive fixed point  in
in  at
at  . Then for every
. Then for every  the operator
the operator  has a fixed point
has a fixed point  at
at  , and
, and 
Proof.
Let  be the fixed point of the operator
be the fixed point of the operator  at
at  . Then
. Then

where  Set
Set

 and
and  Then
Then

where  is also defined by (2.6), which implies that
is also defined by (2.6), which implies that  decreases to a fixed point
decreases to a fixed point  of the operator
of the operator  , and
, and  The proof is complete.
The proof is complete.
Lemma 2.5.
Suppose that (H1)–(H6) hold. Let  have at least one fixed point at
have at least one fixed point at  in
in  . Then
. Then  is bounded above.
is bounded above.
Proof.
Suppose to the contrary that there exists a fixed point sequence  of
of  at
at  such that
such that  Then we need to consider two cases:
Then we need to consider two cases:
-
(i)
there exists a constant
 such that
such that 
-
(ii)
there exists a subsequence
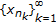 such that
such that 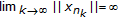 which is impossible by Lemma 2.3.
which is impossible by Lemma 2.3.
Only (i) is considered. We can choose  such that
such that  , and further
, and further  . For
. For  , we have
, we have

Now we consider (2.18). Assume that the case (i) holds. Then

leads to

which is a contradiction. The proof is complete.
Lemma 2.6.
Let  Then
Then  where
where  is defined just as in Lemma 2.5.
is defined just as in Lemma 2.5.
Proof.
In view of Lemma 2.4, it follows that  We only need to prove
We only need to prove  In fact, by the definition of
In fact, by the definition of  , we may choose a distinct nondecreasing sequence
, we may choose a distinct nondecreasing sequence  such that
such that  Let
Let  be the positive fixed point of
be the positive fixed point of  at
at  By Lemma 2.3,
By Lemma 2.3,  is uniformly bounded, so it has a subsequence denoted by
is uniformly bounded, so it has a subsequence denoted by  converging to
converging to  Note that
Note that

Taking the limitation  to both sides of (2.21), and using the Lebesgue dominated convergence theorem [16], we have
to both sides of (2.21), and using the Lebesgue dominated convergence theorem [16], we have

which shows that  has a positive fixed point
has a positive fixed point  at
at  The proof is complete.
The proof is complete.
Theorem 2.7.
Suppose that (H1)–(H6) hold. Then there exists a  such that (1.1) has at least two, one, and no positive solutions for
such that (1.1) has at least two, one, and no positive solutions for  and
and  respectively.
respectively.
Proof.
Assume that (H1)–(H5) hold. Then there exists a  such that
such that  has a fixed point
has a fixed point  at
at  In view of Lemma 2.4,
In view of Lemma 2.4,  also has a fixed point
also has a fixed point  and
and  Note that
Note that  is continuous on
is continuous on  . For
. For  there exists a
there exists a  such that
such that

Hence,

From above, we have

Set  for
for  and
and  . We have
. We have  for
for  By Lemma 2.1,
By Lemma 2.1,  In view of (H6), we can choose
In view of (H6), we can choose  such that
such that

Set

Similar to Lemma 2.3, it is easy to obtain that

In view of Lemma 2.1,  By the additivity of fixed point index,
By the additivity of fixed point index,

So,  has at least two fixed points in
has at least two fixed points in  . The proof is complete.
. The proof is complete.
References
Avery R, Henderson J:Existence of three positive pseudo-symmetric solutions for a one-dimensional
 -Laplacian. Journal of Mathematical Analysis and Applications 2003, 277(2):395-404. 10.1016/S0022-247X(02)00308-6
-Laplacian. Journal of Mathematical Analysis and Applications 2003, 277(2):395-404. 10.1016/S0022-247X(02)00308-6Liu Y, Ge W:Twin positive solutions of boundary value problems for finite difference equations with
 -Laplacian operator. Journal of Mathematical Analysis and Applications 2003, 278(2):551-561. 10.1016/S0022-247X(03)00018-0
-Laplacian operator. Journal of Mathematical Analysis and Applications 2003, 278(2):551-561. 10.1016/S0022-247X(03)00018-0Cabada A:Extremal solutions for the difference
 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.Wong F-H:Existence of positive solutions for
 -Laplacian boundary value problems. Applied Mathematics Letters 1999, 12(3):11-17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999, 12(3):11-17. 10.1016/S0893-9659(98)00164-5Song C:Positive solutions of functional difference equations with
 -Laplacian operator. Advances in Difference Equations 2006, 2006:-9.
-Laplacian operator. Advances in Difference Equations 2006, 2006:-9.Sun H-R, Li W-T: Positive solutions for nonlinear three-point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004, 299(2):508-524. 10.1016/j.jmaa.2004.03.079
Kaufmann ER, Raffoul YN: Positive solutions for a nonlinear functional dynamic equation on a time scale. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(7):1267-1276. 10.1016/j.na.2005.04.031
Luo H, Ma Q: Positive solutions to a generalized second-order three-point boundary-value problem on time scales. Electronic Journal of Differential Equations 2005, 2005(17):1-14.
He Z:Double positive solutions of three-point boundary value problems for
 -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005, 182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005, 182(2):304-315. 10.1016/j.cam.2004.12.012Li W-T, Liu X-L: Eigenvalue problems for second-order nonlinear dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2006, 318(2):578-592. 10.1016/j.jmaa.2005.06.030
Bohner M, Peterson A: Dynamic Equations on Time Scales. An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999, 35(1-2):3-22.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990, 18(1-2):18-56.
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Song C:Existence of solutions for
 -Laplacian functional dynamic equations on time scales. Electronic Journal of Differential Equations 2006, 2006(113):1-8.
-Laplacian functional dynamic equations on time scales. Electronic Journal of Differential Equations 2006, 2006(113):1-8.Aulbach B, Neidhart L: Integration on measure chains. In Proceedings of the 6th International Conference on Difference Equations, July-August 2004, Augsburg, Germany. CRC; 239-252.
Acknowledgments
This work was supported by Grant 10571064 from NNSF of China, and by a grant from NSF of Guangdong.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Song, C. Eigenvalue Problems for  -Laplacian Functional Dynamic Equations on Time Scales.
Adv Differ Equ 2008, 879140 (2008). https://doi.org/10.1155/2008/879140
-Laplacian Functional Dynamic Equations on Time Scales.
Adv Differ Equ 2008, 879140 (2008). https://doi.org/10.1155/2008/879140
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/879140
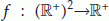 is continuous and nondecreasing about each element;
is continuous and nondecreasing about each element; 
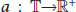 is left dense continuous (i.e.,
is left dense continuous (i.e., 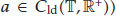 and does not vanish identically on any closed subinterval of
and does not vanish identically on any closed subinterval of  . Here
. Here  denotes the set of all left dense continuous functions from
denotes the set of all left dense continuous functions from 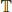 to
to  .
. is continuous and
is continuous and 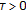 .
.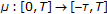 is continuous,
is continuous, 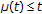 for all
for all 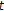 .
.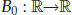 is continuous and nondecreasing;
is continuous and nondecreasing; 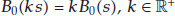 and satisfies that there exist
and satisfies that there exist 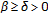 such that
such that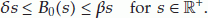
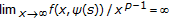 uniformly in
uniformly in 
 for
for 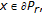 then
then 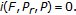
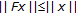 for
for  then
then 
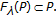
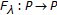 is completely continuous.
is completely continuous. such that
such that 
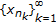 such that
such that 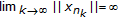 which is impossible by Lemma 2.3.
which is impossible by Lemma 2.3. -Laplacian. Journal of Mathematical Analysis and Applications 2003, 277(2):395-404. 10.1016/S0022-247X(02)00308-6
-Laplacian. Journal of Mathematical Analysis and Applications 2003, 277(2):395-404. 10.1016/S0022-247X(02)00308-6 -Laplacian operator. Journal of Mathematical Analysis and Applications 2003, 278(2):551-561. 10.1016/S0022-247X(03)00018-0
-Laplacian operator. Journal of Mathematical Analysis and Applications 2003, 278(2):551-561. 10.1016/S0022-247X(03)00018-0 -Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601.
-Laplacian problem with nonlinear functional boundary conditions. Computers & Mathematics with Applications 2001, 42(3–5):593-601. -Laplacian boundary value problems. Applied Mathematics Letters 1999, 12(3):11-17. 10.1016/S0893-9659(98)00164-5
-Laplacian boundary value problems. Applied Mathematics Letters 1999, 12(3):11-17. 10.1016/S0893-9659(98)00164-5 -Laplacian operator. Advances in Difference Equations 2006, 2006:-9.
-Laplacian operator. Advances in Difference Equations 2006, 2006:-9. -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005, 182(2):304-315. 10.1016/j.cam.2004.12.012
-Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005, 182(2):304-315. 10.1016/j.cam.2004.12.012 -Laplacian functional dynamic equations on time scales. Electronic Journal of Differential Equations 2006, 2006(113):1-8.
-Laplacian functional dynamic equations on time scales. Electronic Journal of Differential Equations 2006, 2006(113):1-8.