- Research Article
- Open access
- Published:
Exponential Stability of Difference Equations with Several Delays: Recursive Approach
Advances in Difference Equations volume 2009, Article number: 104310 (2009)
Abstract
We obtain new explicit exponential stability results for difference equations with several variable delays and variable coefficients. Several known results, such as Clark's asymptotic stability criterion, are generalized and extended to a new class of equations.
1. Introduction and Preliminaries
In this paper we study stability of a scalar linear difference equation with several delays,

where  is an integer for any
is an integer for any  ,
,  is an integer,
is an integer,  . Stability of (1.1) and relevant nonlinear equations has been an intensively developed area during the last two decades.
. Stability of (1.1) and relevant nonlinear equations has been an intensively developed area during the last two decades.
Let us compare stability methods for delay differential equations and delay difference equations. Many of the methods previously used for differential equations have also been applied to difference equations. However, there are at least two methods which are specific for difference equations. The first approach is reducing a solution of a delay difference equation to the values of a solution of a delay differential equation with piecewise constant arguments at integer points. The second method is based on a recursive form of difference equations and is described in detail later. In this paper we obtain new stability results based on the recursive solution representation.
For (1.1) everywhere below we assume that  ,
,  , that is, the system has a finite memory, and the following initial conditions are defined
, that is, the system has a finite memory, and the following initial conditions are defined

Definition 1.1.
Equation (1.1) is exponentially stable if there exist constants  ,
,  such that for every solution
such that for every solution  of (1.1) and (1.2) the inequality
of (1.1) and (1.2) the inequality

holds for all  , where
, where  do not depend on
do not depend on  .
.
Equation (1.1) is stable if for any  there exists
there exists  such that
such that  implies
implies  ,
,  ; if
; if  does not depend on
does not depend on  , then (1.1) is uniformly stable.
, then (1.1) is uniformly stable.
Equation (1.1) is attractive if for any  a solution tends to zero
a solution tends to zero  . It is asymptotically stable if it is both stable and attractive.
. It is asymptotically stable if it is both stable and attractive.
One of the methods to establish stability of difference equations is based on a recursive form of these equations; see the monographs [1, 2]. The following result was also obtained by this method.
Consider the nonlinear delay difference equation

Assume that  satisfies
satisfies

for some constant  , and for all
, and for all  . Then
. Then

for every solution  of (1.4), where
of (1.4), where  . In particular, the zero solution of (1.4) is globally exponentially stable.
. In particular, the zero solution of (1.4) is globally exponentially stable.
This result was applied to a more general than (1.1) nonlinear difference equation

Without loss of generality, we can suppose that  . We assume that there exist constants
. We assume that there exist constants  such that
such that

for all  and
and  .
.
Similar argument leads to the following result.
Lemma 1.3 ([4]).
Assume that for  large enough inequality (1.8) holds and there exists a constant
large enough inequality (1.8) holds and there exists a constant  such that
such that

Then the zero solution of (1.7) is globally exponentially stable. Moreover, if (1.8) and (1.9) hold for  , then
, then

for every solution  of (1.7).
of (1.7).
Recently several results on exponential stability of high-order difference equations appeared where the results are based on the recursive representations; see, for example, [5, 6]. In particular, in [6, Corollary  ] contains the following statement.
] contains the following statement.
Lemma 1.4 ([6]).
If there exists  such that
such that

for large  , then the zero solution of the equation
, then the zero solution of the equation

is globally exponentially stable.
In the present paper we obtain some new stability results for (1.1) with several variable delays. In contrast to many other stability tests, we consider the case when the sum of coefficients  or some of its subsum is allowed to be in the interval
or some of its subsum is allowed to be in the interval  , not just
, not just  . We illustrate our results with several examples.
. We illustrate our results with several examples.
2. Main Results
Now we can proceed to the main results of this paper. Let us note that any sum where the lower index exceeds the upper index is assumed to vanish.
Theorem 2.1.
Suppose that there exist a set of indices  and
and  such that for
such that for  sufficiently large
sufficiently large

Then (1.1) is exponentially stable.
Proof.
Since

then

By Lemma 1.2, (1.1) is exponentially stable.
We can reformulate Theorem 2.1 in the following equivalent form.
Theorem 2.2.
Suppose that there exist a set of indices and
and  such that for
such that for  sufficiently large
sufficiently large

Then (1.1) is exponentially stable.
Assuming first  and then
and then  we obtain the following two corollaries for an equation with a nondelay term.
we obtain the following two corollaries for an equation with a nondelay term.
Corollary 2.3.
Let  and
and  for
for  large enough. Then the equation
large enough. Then the equation

is exponentially stable.
Example 2.4.
Consider the equation

with an arbitrary bounded delay  :
:  for some integer
for some integer  and any
and any  . Since
. Since  , then by Corollary 2.3 this equation is exponentially stable. Lemma 1.4 is formulated for a constant delay, some other tests do not apply since
, then by Corollary 2.3 this equation is exponentially stable. Lemma 1.4 is formulated for a constant delay, some other tests do not apply since  .
.
Corollary 2.5.
Suppose that for some  the following inequality is satisfied for
the following inequality is satisfied for  large enough:
large enough:

Then (2.5) is exponentially stable.
Example 2.6.
By Corollary 2.5 the equation

is exponentially stable, since  and
and  .
.
Now let us assume that all coefficients are proportional. Such equations arise as linear approximations of nonlinear difference equations in mathematical biology. Then a straightforward computation leads to the following result.
Corollary 2.7.
Suppose that all coefficients are proportional  ,
,  there exist
there exist  ,
,  and a set of indices
and a set of indices  , such that
, such that  and
and

Then (1.1) is exponentially stable.
Assuming constant coefficients and  we obtain the following corollary.
we obtain the following corollary.
Corollary 2.8.
Suppose that all coefficients are constants  and
and

Then (1.1) is exponentially stable.
Remark 2.9.
Corollary 2.8 for the case  was obtained in Proposition
was obtained in Proposition  of [7].
of [7].
Now let us consider the equation with one nondelay and one delay terms

Choosing  ,
,  , we obtain Parts
, we obtain Parts  and
and  of Corollary 2.10, respectively.
of Corollary 2.10, respectively.
Corollary 2.10.
Suppose that there exists  such that at least one of the following conditions holds for
such that at least one of the following conditions holds for  sufficiently large:
sufficiently large:
-
(1)
 ;
; -
(2)

Then (2.11) is exponentially stable.
Let us now proceed to equations with three terms in the right-hand side

For  and
and  we obtain Parts
we obtain Parts  ,
,  ,
,  and
and  , respectively.
, respectively.
Corollary 2.11.
Suppose that there exists  such that at least one of the following conditions holds for
such that at least one of the following conditions holds for  sufficiently large:
sufficiently large:
-
(1)
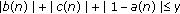 ;
; -
(2)
 ;
; -
(3)
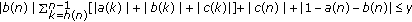 ;
; -
(4)
 .
.
Then (2.12) is exponentially stable.
Theorem 2.1 and its corollaries imply new explicit conditions of exponential stability for autonomous difference equations with several delays, as well as a new justification for known ones.
Consider the autonomous equation

where  . Choosing
. Choosing  we immediately obtain the following stability test.
we immediately obtain the following stability test.
Corollary 2.12.
Let  . Then (2.13) is exponentially stable.
. Then (2.13) is exponentially stable.
Remark 2.13.
This result is well known; see, for example, [8] for  as well as some results for autonomous equations below. We presented it just to illustrate our method.
as well as some results for autonomous equations below. We presented it just to illustrate our method.
Further, Theorem 2.1 and Corollaries 2.8 and 2.11 can be reformulated for (2.13) as follows.
Corollary 2.14.
Suppose that there exists a set of indices  , with
, with  such that
such that

Then (2.13) is exponentially stable.
Corollary 2.15.
If  , then (2.13) is exponentially stable.
, then (2.13) is exponentially stable.
Consider now an autonomous equation with two delays:

where 
Corollary 2.16.
Suppose that at least one of the following conditions holds
-
(1)
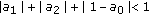 ;
; -
(2)
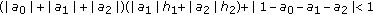 ;
; -
(3)
 ;
; -
(4)
 .
.
Then (2.15) is exponentially stable.
Let us present two more results which can be easily deduced from the recursive representation of solutions. To this end we consider the equation

which is a different form of (1.1).
We recall that we assume  for all delays
for all delays  in this paper.
in this paper.
Theorem 2.17.
Suppose that there exists  such that
such that

Then (2.16) is exponentially stable.
Proof.
Without loss of generality we can assume that the expression under  in (2.17) does not exceed some
in (2.17) does not exceed some  for
for  . Since
. Since

then

Hence for  we have
we have

Thus by Lemma 1.2 , where
, where  ,
,  , for
, for  , so (2.16) is exponentially stable.
, so (2.16) is exponentially stable.
Theorem 2.18.
Suppose that there exists  ,
,  such that
such that

Then (2.16) is exponentially stable.
Proof.
Without loss of generality we can assume that the expression under  in (2.21) does not exceed some
in (2.21) does not exceed some  for
for  . Since
. Since

then the reference to Lemma 1.2 completes the proof.
3. Discussion and Examples
Let us comment that Theorem 2.18 (see also Corollary 2.12) generalizes the result of Clark [8] that  is a sufficient condition for the asymptotic stability of the difference equation
is a sufficient condition for the asymptotic stability of the difference equation

We note that there are not really many publications on difference equations with variable delays, and the present paper partially fills up this gap. In particular, Theorem 2.18 gives the same stability condition for the equation with variable delays

once the delays are bounded:  ,
,  .
.
The following example outlines the sharpness of the condition that the delays are bounded in Theorems 2.1, 2.2, 2.17, and 2.18.
Example 3.1.
The equation with constant coefficients

satisfies all assumptions of Theorems 2.1, 2.2, 2.17, and 2.18 but the boundedness of the delay. Since the solution  with
with  tends to 1 as
tends to 1 as  , then the zero solution of (3.3) is neither asymptotically nor exponentially stable. Here even the condition
, then the zero solution of (3.3) is neither asymptotically nor exponentially stable. Here even the condition  is not satisfied.
is not satisfied.
Example 3.2.
Let us demonstrate that in the case when the arguments tend to infinity but the delays are not bounded and all other conditions of Theorem 2.18 are satisfied, this does not imply exponential stability. The equation

where  is the integer part of
is the integer part of  , is asymptotically, but not exponentially stable. Really, its solution
, is asymptotically, but not exponentially stable. Really, its solution

is nonincreasing by the absolute value and

for any  ,
,  , so
, so  for any
for any  ; the equation is asymptotically stable. Since the solution decay is not faster than
; the equation is asymptotically stable. Since the solution decay is not faster than  , then the equation is not exponentially stable.
, then the equation is not exponentially stable.
Next, let us compare Corollary 2.10 and Theorem  of [6] which is also Lemma 1.4 of the present paper.
of [6] which is also Lemma 1.4 of the present paper.
Example 3.3.
Consider (1.12), where

Then, (1.12) is exponentially stable for any  by Corollary 2.10, Part (
by Corollary 2.10, Part ( ; here
; here  ,
,  .
.
If, for example, we assume  , then (1.11) has the form
, then (1.11) has the form

which is not satisfied for even  , so Lemma 1.4 cannot be applied to deduce exponential stability.
, so Lemma 1.4 cannot be applied to deduce exponential stability.
Example 3.4.
We will modify Example  in [6] to compare Theorem 2.18 and Lemma 1.4. Consider
in [6] to compare Theorem 2.18 and Lemma 1.4. Consider

Let us compare constants  such that (1.12) is exponentially stable for
such that (1.12) is exponentially stable for 

By Theorem 2.18 we obtain stability whenever

Condition (3.8) of Lemma 1.4 becomes

for even  and
and

for odd  , which gives the intervals
, which gives the intervals  and
and  , respectively. Finally, Lemma 1.4 implies exponential stability for
, respectively. Finally, Lemma 1.4 implies exponential stability for  .
.
In addition to Theorems 2.1, 2.2, 2.17, and 2.18, let us review some other known stability conditions for equations with several delays. For comparison, we will cite the following two results.
Suppose that

Then the equation with several delays

is globally asymptotically stable.
Theorem 3 B ([15]).
Suppose that  and
and

Then (1.1) is asymptotically stable.
Let us note that unlike Theorems A and B we do not assume that coefficients are either nonnegative (as in Theorem A) or constant (as in Theorem B). Further, let us compare our stability tests with known results, including Theorems A and B.
Example 3.5.
Consider the equation

where

Repeating the proof of Theorem 2.17, we have

By Theorem 2.17, (3.17) is exponentially stable since

Lemma 1.4 cannot be applied since for even 

Theorem A fails since

Theorem B is applicable to equations with constant coefficients only.
References
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Elaydi S: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 3rd edition. Springer, New York, NY, USA; 2005:xxii+539.
Stević S: Behavior of the positive solutions of the generalized Beddington-Holt equation. Panamerican Mathematical Journal 2000,10(4):77-85.
Berezansky L, Braverman E, Liz E: Sufficient conditions for the global stability of nonautonomous higher order difference equations. Journal of Difference Equations and Applications 2005,11(9):785-798. 10.1080/10236190500141050
Liz E: On explicit conditions for the asymptotic stability of linear higher order difference equations. Journal of Mathematical Analysis and Applications 2005,303(2):492-498. 10.1016/j.jmaa.2004.08.048
El-Morshedy HA: New explicit global asymptotic stability criteria for higher order difference equations. Journal of Mathematical Analysis and Applications 2007,336(1):262-276. 10.1016/j.jmaa.2006.12.049
Győri I, Hartung F, Turi J: On the effects of delay perturbations on the stability of delay difference equations. In Proceedings of the 1st International Conference on Difference Equations (San Antonio, Tex, 1994). Gordon and Breach, Luxembourg, UK; 1995:237-253.
Clark CW: A delayed-recruitment model of population dynamics, with an application to baleen whale populations. Journal of Mathematical Biology 1976,3(3-4):381-391. 10.1007/BF00275067
Erbe LH, Xia H, Yu JS: Global stability of a linear nonautonomous delay difference equation. Journal of Difference Equations and Applications 1995,1(2):151-161. 10.1080/10236199508808016
Yu JS: Asymptotic stability for a linear difference equation with variable delay. Computers & Mathematics with Applications 1998,36(10–12):203-210.
Zhang BG, Tian CJ, Wong PJY: Global attractivity of difference equations with variable delay. Dynamics of Continuous, Discrete and Impulsive Systems 1999,6(3):307-317.
Malygina VV, Kulikov AY: On precision of constants in some theorems on stability of difference equations. Functional Differential Equations 2008,15(3-4):239-248.
Matsunaga H, Hara T, Sakata S: Global attractivity for a nonlinear difference equation with variable delay. Computers & Mathematics with Applications 2001,41(5-6):543-551. 10.1016/S0898-1221(00)00297-2
Muroya Y, Ishiwata E, Guglielmi N: Global stability for nonlinear difference equations with variable coefficients. Journal of Mathematical Analysis and Applications 2007,334(1):232-247. 10.1016/j.jmaa.2006.12.028
Győri I, Hartung F: Stability in delay perturbed differential and difference equations. In Topics in Functional Differential and Difference Equations (Lisbon, 1999), Fields Institute Communications. Volume 29. American Mathematical Society, Providence, RI, USA; 2001:181-194.
Acknowledgments
The authors are very grateful to the referee for valuable comments and remarks. This paper is partially supported by Israeli Ministry of Absorption and by the NSERC Research Grant.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Berezansky, L., Braverman, E. Exponential Stability of Difference Equations with Several Delays: Recursive Approach. Adv Differ Equ 2009, 104310 (2009). https://doi.org/10.1155/2009/104310
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/104310
 ;
;
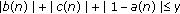 ;
; ;
;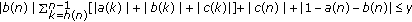 ;
; .
.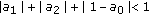 ;
;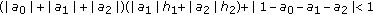 ;
; ;
; .
.