- Research Article
- Open access
- Published:
Global Dynamics of a Competitive System of Rational Difference Equations in the Plane
Advances in Difference Equations volume 2009, Article number: 132802 (2010)
Abstract
We investigate global dynamics of the following systems of difference equations  ,
,  ,
,  , where the parameters
, where the parameters  ,
,  ,
,  ,
,  , and
, and  are positive numbers and initial conditions
are positive numbers and initial conditions  and
and  are arbitrary nonnegative numbers such that
are arbitrary nonnegative numbers such that  . We show that this system has rich dynamics which depend on the part of parametric space. We show that the basins of attractions of different locally asymptotically stable equilibrium points are separated by the global stable manifolds of either saddle points or of nonhyperbolic equilibrium points.
. We show that this system has rich dynamics which depend on the part of parametric space. We show that the basins of attractions of different locally asymptotically stable equilibrium points are separated by the global stable manifolds of either saddle points or of nonhyperbolic equilibrium points.
1. Introduction and Preliminaries
In this paper, we study the global dynamics of the following rational system of difference equations:

where the parameters  and
and  are positive numbers and initial conditions
are positive numbers and initial conditions  and
and  are arbitrary numbers. System (1.1) was mentioned in [1] as a part of Open Problem 3 which asked for a description of global dynamics of three specific competitive systems. According to the labeling in [1], system (1.1) is called
are arbitrary numbers. System (1.1) was mentioned in [1] as a part of Open Problem 3 which asked for a description of global dynamics of three specific competitive systems. According to the labeling in [1], system (1.1) is called  . In this paper, we provide the precise description of global dynamics of system (1.1). We show that system (1.1) has a variety of dynamics that depend on the value of parameters. We show that system (1.1) may have between zero and two equilibrium points, which may have different local character. If system (1.1) has one equilibrium point, then this point is either locally saddle point or non-hyperbolic. If system (1.1) has two equilibrium points, then the pair of points is the pair of a saddle point and a sink. The major problem is determining the basins of attraction of different equilibrium points. System (1.1) gives an example of semistable non-hyperbolic equilibrium point. The typical results are Theorems 4.1 and 4.5 below.
. In this paper, we provide the precise description of global dynamics of system (1.1). We show that system (1.1) has a variety of dynamics that depend on the value of parameters. We show that system (1.1) may have between zero and two equilibrium points, which may have different local character. If system (1.1) has one equilibrium point, then this point is either locally saddle point or non-hyperbolic. If system (1.1) has two equilibrium points, then the pair of points is the pair of a saddle point and a sink. The major problem is determining the basins of attraction of different equilibrium points. System (1.1) gives an example of semistable non-hyperbolic equilibrium point. The typical results are Theorems 4.1 and 4.5 below.
System (1.1) is a competitive system, and our results are based on recent results developed for competitive systems in the plane; see [2, 3]. In the next section, we present some general results about competitive systems in the plane. The third section deals with some basic facts such as the non-existence of period-two solution of system (1.1). The fourth section analyzes local stability which is fairly complicated for this system. Finally, the fifth section gives global dynamics for all values of parameters.
Let  and
and  be intervals of real numbers. Consider a first-order system of difference equations of the form
be intervals of real numbers. Consider a first-order system of difference equations of the form

where 
When the function  is increasing in
is increasing in  and decreasing in
and decreasing in  and the function
and the function  is decreasing in
is decreasing in  and increasing in
and increasing in  , the system (1.2) is called competitive. When the function
, the system (1.2) is called competitive. When the function  is increasing in
is increasing in  and increasing in
and increasing in  and the function
and the function  is increasing in
is increasing in  and increasing in
and increasing in  the system (1.2) is called cooperative. A map
the system (1.2) is called cooperative. A map  that corresponds to the system (1.2) is defined as
that corresponds to the system (1.2) is defined as  . Competitive and cooperative maps, which are called monotone maps, are defined similarly. Strongly competitive systems of difference equations or maps are those for which the functions
. Competitive and cooperative maps, which are called monotone maps, are defined similarly. Strongly competitive systems of difference equations or maps are those for which the functions  and
and  are coordinate-wise strictly monotone.
are coordinate-wise strictly monotone.
If  , we denote with
, we denote with  , the four quadrants in
, the four quadrants in  relative to
relative to  , that is,
, that is,  , and so on. Define the South-East partial order
, and so on. Define the South-East partial order  on
on  by
by  if and only if
if and only if  and
and  . Similarly, we define the North-East partial order
. Similarly, we define the North-East partial order  on
on  by
by  if and only if
if and only if  and
and  . For
. For  and
and  , define the distance from
, define the distance from to
to as
as  . By
. By  we denote the interior of a set
we denote the interior of a set  .
.
It is easy to show that a map  is competitive if it is nondecreasing with respect to the South-East partial order, that is if the following holds:
is competitive if it is nondecreasing with respect to the South-East partial order, that is if the following holds:

Competitive systems were studied by many authors; see [4–19], and others. All known results, with the exception of [4, 6, 10], deal with hyperbolic dynamics. The results presented here are results that hold in both the hyperbolic and the non-hyperbolic cases.
We now state three results for competitive maps in the plane. The following definition is from [18].
Definition 1.1.
Let  be a nonempty subset of
be a nonempty subset of  . A competitive map
. A competitive map  is said to satisfy condition (
is said to satisfy condition ( ) if for every
) if for every  ,
,  in
in  ,
,  implies
implies  , and
, and  is said to satisfy condition (
is said to satisfy condition ( ) if for every
) if for every  ,
,  in
in  ,
,  implies
implies  .
.
The following theorem was proved by de Mottoni and Schiaffino [20] for the Poincaré map of a periodic competitive Lotka-Volterra system of differential equations. Smith generalized the proof to competitive and cooperative maps [15, 16].
Theorem 1.2.
Let  be a nonempty subset of
be a nonempty subset of  . If
. If  is a competitive map for which (
is a competitive map for which ( ) holds, then for all
) holds, then for all  ,
,  is eventually componentwise monotone. If the orbit of
is eventually componentwise monotone. If the orbit of  has compact closure, then it converges to a fixed point of
has compact closure, then it converges to a fixed point of  . If instead (
. If instead ( ) holds, then for all
) holds, then for all  ,
,  is eventually componentwise monotone. If the orbit of
is eventually componentwise monotone. If the orbit of  has compact closure in
has compact closure in  , then its omega limit set is either a period-two orbit or a fixed point.
, then its omega limit set is either a period-two orbit or a fixed point.
The following result is from [18], with the domain of the map specialized to be the Cartesian product of intervals of real numbers. It gives a sufficient condition for conditions ( ) and (
) and ( ).
).
Theorem 1.3 (Smith [18]).
Let  be the Cartesian product of two intervals in
be the Cartesian product of two intervals in  . Let
. Let  be a
be a  competitive map. If
competitive map. If  is injective and
is injective and  for all
for all  then
then  satisfies (
satisfies ( ). If
). If  is injective and
is injective and  for all
for all  then
then  satisfies (
satisfies ( ).
).
Theorem 1.4.
Let  be a monotone map on a closed and bounded rectangular region
be a monotone map on a closed and bounded rectangular region  Suppose that
Suppose that  has a unique fixed point
has a unique fixed point  in
in  Then
Then  is a global attractor of
is a global attractor of  on
on 
The following theorems were proved by Kulenović and Merino [3] for competitive systems in the plane, when one of the eigenvalues of the linearized system at an equilibrium (hyperbolic or non-hyperbolic) is by absolute value smaller than  while the other has an arbitrary value. These results are useful for determining basins of attraction of fixed points of competitive maps.
while the other has an arbitrary value. These results are useful for determining basins of attraction of fixed points of competitive maps.
Our first result gives conditions for the existence of a global invariant curve through a fixed point (hyperbolic or not) of a competitive map that is differentiable in a neighborhood of the fixed point, when at least one of two nonzero eigenvalues of the Jacobian matrix of the map at the fixed point has absolute value less than one. A region  is rectangular if it is the Cartesian product of two intervals in
is rectangular if it is the Cartesian product of two intervals in  .
.
Theorem 1.5.
Let  be a competitive map on a rectangular region
be a competitive map on a rectangular region  . Let
. Let  be a fixed point of
be a fixed point of  such that
such that  is nonempty (i.e.,
is nonempty (i.e.,  is not the NW or SE vertex of
is not the NW or SE vertex of  , and
, and  is strongly competitive on
is strongly competitive on  . Suppose that the following statements are true.
. Suppose that the following statements are true.
-
(a)
The map
 has a
has a  extension to a neighborhood of
extension to a neighborhood of  .
. -
(b)
The Jacobian matrix of
 at
at  has real eigenvalues
has real eigenvalues  ,
,  such that
such that  , where
, where  , and the eigenspace
, and the eigenspace  associated with
associated with  is not a coordinate axis.
is not a coordinate axis.
Then there exists a curve  through
through  that is invariant and a subset of the basin of attraction of
that is invariant and a subset of the basin of attraction of  , such that
, such that  is tangential to the eigenspace
is tangential to the eigenspace  at
at  , and
, and  is the graph of a strictly increasing continuous function of the first coordinate on an interval. Any endpoints of
is the graph of a strictly increasing continuous function of the first coordinate on an interval. Any endpoints of  in the interior of
in the interior of  are either fixed points or minimal period-two points. In the latter case, the set of endpoints of
are either fixed points or minimal period-two points. In the latter case, the set of endpoints of  is a minimal period-two orbit of
is a minimal period-two orbit of  .
.
Corollary 1.6.
If  has no fixed point nor periodic points of minimal period-two in
has no fixed point nor periodic points of minimal period-two in  , then the endpoints of
, then the endpoints of  belong to
belong to  .
.
For maps that are strongly competitive near the fixed point, hypothesis b. of Theorem 1.5 reduces just to  . This follows from a change of variables [18] that allows the Perron-Frobenius Theorem to be applied to give that, at any point, the Jacobian matrix of a strongly competitive map has two real and distinct eigenvalues, the larger one in absolute value being positive, and that corresponding eigenvectors may be chosen to point in the direction of the second and first quadrants, respectively. Also, one can show that in such case no associated eigenvector is aligned with a coordinate axis.
. This follows from a change of variables [18] that allows the Perron-Frobenius Theorem to be applied to give that, at any point, the Jacobian matrix of a strongly competitive map has two real and distinct eigenvalues, the larger one in absolute value being positive, and that corresponding eigenvectors may be chosen to point in the direction of the second and first quadrants, respectively. Also, one can show that in such case no associated eigenvector is aligned with a coordinate axis.
The following result gives a description of the global stable and unstable manifolds of a saddle point of a competitive map. The result is the modification of Theorem 1.7 from [12].
Theorem 1.7.
In addition to the hypotheses of Theorem 1.5, suppose that  and that the eigenspace
and that the eigenspace  associated with
associated with  is not a coordinate axis. If the curve
is not a coordinate axis. If the curve  of Theorem 1.5 has endpoints in
of Theorem 1.5 has endpoints in  , then
, then  is the global stable manifold
is the global stable manifold  of
of  , and the global unstable manifold
, and the global unstable manifold  is a curve in
is a curve in  that is tangential to
that is tangential to  at
at  and such that it is the graph of a strictly decreasing function of the first coordinate on an interval. Any endpoints of
and such that it is the graph of a strictly decreasing function of the first coordinate on an interval. Any endpoints of  in
in  are fixed points of
are fixed points of  .
.
The next result is useful for determining basins of attraction of fixed points of competitive maps.
Theorem 1.8.
Assume the hypotheses of Theorem 1.5, and let  be the curve whose existence is guaranteed by Theorem 1.5. If the endpoints of
be the curve whose existence is guaranteed by Theorem 1.5. If the endpoints of  belong to
belong to  , then
, then  separates
separates  into two connected components, namely
into two connected components, namely

such that the following statements are true.
-
(i)
 is invariant, and
is invariant, and  as
as  for every
for every  .
. -
(ii)
 is invariant, and
is invariant, and  as
as  for every
for every  .
.
If, in addition,  is an interior point of
is an interior point of  and
and  is
is  and strongly competitive in a neighborhood of
and strongly competitive in a neighborhood of  , then
, then  has no periodic points in the boundary of
has no periodic points in the boundary of  except for
except for  , and the following statements are true.
, and the following statements are true.
-
(iii)
For every
 there exists
there exists  such that
such that  for
for  .
. -
(iv)
For every
 there exists
there exists  such that
such that  for
for  .
.
2. Some Basic Facts
In this section we give some basic facts about the nonexistence of period-two solutions, local injectivity of map  at the equilibrium point and
at the equilibrium point and  condition.
condition.
2.1. Equilibrium Points
The equilibrium points  of system (1.1) satisfy
of system (1.1) satisfy

First equation of System (2.1) gives

Second equation of System (2.1) gives

Now, using (2.2), we obtain

This implies

which is equivalent to

Solutions of (2.6) are

Now, (2.2) gives

The equilibrium points are:

where  are given by the above relations.
are given by the above relations.
Note that

The discriminant of (2.6) is given by

The criteria for the existence of equilibrium points are summarized in Table 1 where

2.2. Condition  and Period-Two Solution
and Period-Two Solution
In this section we prove three lemmas.
Lemma 2.1.
System (1.1) satisfies either  or
or  Consequently, the second iterate of every solution is eventually monotone.
Consequently, the second iterate of every solution is eventually monotone.
Proof.
The map  associated to system (1.1) is given by
associated to system (1.1) is given by

Assume

then we have


Equations (2.15) and (2.16) are equivalent, respectively, to


Now, using (2.17) and (2.18), we have the following:

Lemma 2.2.
System (1.1) has no minimal period-two solution.
Proof.
Set

Then

Period-two solution satisfies


We show that this system has no other positive solutions except equilibrium points.
Equations (2.22) and (2.23) are equivalent, respectively, to


Equation (2.24) implies

Equation (2.25) implies

Using (2.26), we have

Putting (2.28) into (2.27), we have

This is equivalent to

Putting (2.30) into (2.24), we obtain

or

From (2.31), we obtain fixed points. In the sequel, we consider (2.32).
Discriminant of (2.32) is given by

Real solutions of (2.32) exist if and only if  The solutions are given by
The solutions are given by

Using (2.30), we have

Claim.
Assume  Then
Then
-
(i)
for all values of parameters,

-
(ii)
for all values of parameters,

Proof.
( ) Assume
) Assume  Then it is obvious that the claim
Then it is obvious that the claim  is true. Now, assume
is true. Now, assume  Then
Then  if and only if
if and only if

which is equivalent to

This is true since

( ) Assume
) Assume  Then it is obvious that
Then it is obvious that  . Now, assume
. Now, assume

Then  if and only if
if and only if

This is equivalent to

Using (2.39), we have

which implies that the inequality (2.41) is true.
Now, the proof of the Lemma 2.2 follows from the Claim .
Lemma 2.3.
The map  associated to System (1.1) satisfies the following:
associated to System (1.1) satisfies the following:

Proof.
By using (2.1), we have

First equation implies

Second equation implies

Note the following

Using (2.47), Equations (2.45) and (2.46), respectively, become

Note that System (2.48) is linear homogeneous system in  and
and  The determinant of System (2.48) is given by
The determinant of System (2.48) is given by

Using (2.1), the determinant of System (2.48) becomes

This implies that System (2.48) has only trivial solution, that is

3. Linearized Stability Analysis
The Jacobian matrix of the map  has the following form:
has the following form:

The value of the Jacobian matrix of  at the equilibrium point is
at the equilibrium point is

The determinant of (3.2) is given by

The trace of (3.2) is

The characteristic equation has the form

Theorem 3.1.
Assume that  Then there exists a unique positive equilibrium
Then there exists a unique positive equilibrium  which is a saddle point, and the following statements hold.
which is a saddle point, and the following statements hold.
-
(a)
If
 then
then  and
and 
-
(b)
If
 and
and  then
then  and
and 
-
(c)
If
 and
and  then
then  and
and 
-
(d)
If
 and
and  then
then  and
and 
Proof.
The equilibrium is a saddle point if and only if the following conditions are satisfied:

The first condition is equivalent to

This implies the following:

Notice the following:

That is,

Similarly,

Now, we have

This is equivalent to

The last condition is equivalent to

which is true since  and
and 
The second condition is equivalent to

This is equivalent to

establishing the proof of Theorem 3.1.
Since the map  is strongly competitive, the Jacobian matrix (3.2) has two real and distinct eigenvalues, with the larger one in absolute value being positive.
is strongly competitive, the Jacobian matrix (3.2) has two real and distinct eigenvalues, with the larger one in absolute value being positive.
From (3.5) at  we have
we have

The first equation implies that either both eigenvalues are positive or the smaller one is negative.
Consider the numerator of the right-hand side of the second equation. We have

where 
(a) If  then the smaller root is negative, that is,
then the smaller root is negative, that is, 
If  then
then

From the last inequality statements  and
and  follow.
follow.
We now perform a similar analysis for the other cases in Table 1.
Theorem 3.2.
Assume

Then  exist.
exist.  is a saddle point;
is a saddle point;  is a sink. For the eigenvalues of
is a sink. For the eigenvalues of  the following holds.
the following holds.
-
(a)
If
 then
then 
-
(b)
If
 and
and  then
then 
-
(c)
If
 and
and  then
then 
Proof.
Note that if  and
and  then
then  and
and  which implies
which implies  , which is a contradiction.
, which is a contradiction.
The equilibrium is a sink if the following condition is satisfied:

The condition  is equivalent to
is equivalent to

This implies

Now, we prove that  is a sink.
is a sink.
We have to prove that

Notice the following:

Similarly,

Now, condition

becomes

that is,

which is true. (see Theorem 3.1.)
Condition

is equivalent to

This implies

We have to prove that

Using (2.2), we have

This is equivalent to

which is always true since  and the left side is always negative, while the right side is always positive.
and the left side is always negative, while the right side is always positive.
Notice that conditions

imply that  is a saddle point.
is a saddle point.
From (3.5) at  we have
we have

The first equation implies that either both eigenvalues are positive or the smaller one is negative.
Consider the numerator of the right-hand side of the second equation. We have

We have

Inequality

is equivalent to

which is obvious if  . Then inequality (3.41) holds. This confirms
. Then inequality (3.41) holds. This confirms  The other cases follow from (3.41).
The other cases follow from (3.41).
Theorem 3.3.
Assume

Then there exists a unique positive equilibrium point

which is non-hyperbolic. The following holds.
-
(a)
If
 then
then  and
and 
-
(b)
If
 then
then  and
and 
Proof.
Evaluating the Jacobian matrix (3.2) at equilibrium  we have
we have

The characteristic equation of  is
is

which is simplified to

Solutions of (3.46) are

Note that  can be written in the following form:
can be written in the following form:

Note that 
The corresponding eigenvectors, respectively, are

Note that the denominator of (3.48) is always positive.
Consider numerator of (3.48)

From

we have

Substituting  from (3.52) in (3.50), we obtain
from (3.52) in (3.50), we obtain

Now, (3.48) becomes

establishing the proof of the theorem.
Now, we consider the special case of System (1.1) when 
In this case system (1.1) becomes

Equilibrium points are solutions of the following system:

The second equation implies

Now, the first equation implies

The map  associated to System (3.55) is given by
associated to System (3.55) is given by

The Jacobian matrix of the map  has the following form:
has the following form:

The value of the Jacobian matrix of  at the equilibrium point is
at the equilibrium point is

The determinant of (3.61) is given by

The trace of (3.61) is

Theorem 3.4.
Assume

Then there exists a unique positive equilibrium point

of system (1.1), which is a saddle point. The following statements hold.
-
(a)
If
 then
then 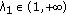 and
and 
-
(b)
If
 then
then  and
and 
Proof.
We prove that  is a saddle point.
is a saddle point.
We check the conditions

Condition  is equivalent to
is equivalent to

This implies

Condition

is equivalent to

Hence  is a saddle point.
is a saddle point.
Now,

The first equation implies that either both eigenvalues are positive or the smaller one is less then zero. The second equation implies that

establishing the proof of theorem.
4. Global Behavior
Theorem 4.1.
Assume

Then system (1.1) has a unique equilibrium point  which is a saddle point. Furthermore, there exists the global stable manifold
which is a saddle point. Furthermore, there exists the global stable manifold  that separates the positive quadrant so that all orbits below this manifold are asymptotic to
that separates the positive quadrant so that all orbits below this manifold are asymptotic to  and all orbits above this manifold are asymptotic to
and all orbits above this manifold are asymptotic to  All orbits that start on
All orbits that start on  are attracted to
are attracted to  The global unstable manifold
The global unstable manifold  is the graph of a continuous, unbounded, strictly decreasing function.
is the graph of a continuous, unbounded, strictly decreasing function.
Proof.
The existence of the global stable manifold  with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
Theorem 4.2.
Assume

Then system (1.1) has two equilibrium points:  which is a saddle point and
which is a saddle point and  which is a sink. Furthermore, there exists the global stable manifold
which is a sink. Furthermore, there exists the global stable manifold  that separates the positive quadrant so that all orbits below this manifold are asymptotic to
that separates the positive quadrant so that all orbits below this manifold are asymptotic to  and all orbits above this manifold are attracted to equilibrium
and all orbits above this manifold are attracted to equilibrium  All orbits that start on
All orbits that start on  are attracted to
are attracted to  The global unstable manifold
The global unstable manifold  is the graph of a continuous, unbounded, strictly decreasing function with end point
is the graph of a continuous, unbounded, strictly decreasing function with end point 
Proof.
The existence of the global stable manifold  with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
Theorem 4.3.
Assume

Then system (1.1) has a unique equilibrium  which is non-hyperbolic. The sequences
which is non-hyperbolic. The sequences  , and
, and  are eventually monotonic. Every solution that starts in
are eventually monotonic. Every solution that starts in  is asymptotic to
is asymptotic to  and every solution that starts in
and every solution that starts in  is asymptotic to the equilibrium
is asymptotic to the equilibrium  Furthermore, there exists the global stable manifold
Furthermore, there exists the global stable manifold  that separates the positive quadrant into three invariant regions, so that all orbits below this manifold are asymptotic to
that separates the positive quadrant into three invariant regions, so that all orbits below this manifold are asymptotic to  and all orbits that start above this manifold are attracted to the equilibrium
and all orbits that start above this manifold are attracted to the equilibrium  All orbits that start on
All orbits that start on  are attracted to
are attracted to 
Proof.
The existence of the global stable manifold  with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
First we prove that for all points  the following holds:
the following holds:

Observe that  is actually an arbitrary point on the curve
is actually an arbitrary point on the curve  , which represents one of two equilibrium curves for system (1.1).
, which represents one of two equilibrium curves for system (1.1).
Indeed,

Now we have

The last inequality is equivalent to

This is equivalent to

which always holds since the discriminant of the quadratic polynomial on the left-hand side is zero.
Note that  and
and  for
for 
Monotonicity of the map  implies
implies

Set  Then the sequence
Then the sequence  is increasing and bounded by
is increasing and bounded by  coordinate of the equilibrium, and the sequence
coordinate of the equilibrium, and the sequence  is decreasing and bounded by
is decreasing and bounded by  coordinate of the equilibrium. This implies that
coordinate of the equilibrium. This implies that  converges to the equilibrium as
converges to the equilibrium as 
Now, take any point  Then there exists point
Then there exists point  such that
such that  By using monotonicity of the map
By using monotonicity of the map  we obtain
we obtain

Letting  in (4.10), we have
in (4.10), we have

Now, we consider  By choosing
By choosing  such that
such that  , we note that
, we note that

By using monotonicity of the map  we have
we have

Set  Then the sequence
Then the sequence  is increasing, and the sequence
is increasing, and the sequence  is decreasing and bounded by
is decreasing and bounded by  coordinate of equilibrium and has to converge. If
coordinate of equilibrium and has to converge. If  converges, then
converges, then  has to converge to the equilibrium, which is impossible. This implies that
has to converge to the equilibrium, which is impossible. This implies that  Since
Since  then
then 
Now, take any point  in
in  . Then there is point
. Then there is point  such that
such that  Using monotonicity of the map
Using monotonicity of the map  we have
we have

Since,  is asymptotic to
is asymptotic to  then
then 
Theorem 4.4.
Assume

Then system (1.1) has a unique equilibrium  which is a saddle point. Furthermore, there exists the global stable manifold
which is a saddle point. Furthermore, there exists the global stable manifold  that separates the positive quadrant so that all orbits below this manifold are asymptotic to
that separates the positive quadrant so that all orbits below this manifold are asymptotic to  and all orbits above this manifold are asymptotic to
and all orbits above this manifold are asymptotic to  All orbits that start on
All orbits that start on  are attracted to
are attracted to  The global stable manifold
The global stable manifold  is the graph of a continuous, unbounded, strictly increasing function.
is the graph of a continuous, unbounded, strictly increasing function.
Proof.
The existence of the global stable manifold  with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
with the stated properties follows from Theorems 1.5, 1.7, and 1.8 and Lemmas 2.1 and 2.2.
Theorem 4.5.
Assume


or

Then system (1.1) does not possess an equilibrium point. Its global behavior is described as follows:

Proof.
If the conditions of this theorem are satisfied, then (2.6) implies that there is no real (if the first condition of this theorem is satisfied) or positive equilibrium points (if the second condition of this theorem is satisfied).
Consider the second equation of system (1.1). That is,

Note the following

Now, consider equation

Its solution is given by

Since  then letting
then letting  we obtain that
we obtain that  Now, (4.21) implies
Now, (4.21) implies

This means that sequence  is bounded for
is bounded for 
In order to prove the global behavior in this case, we decompose System (1.1) into the system of even-indexed and odd-indexed terms as

for  .
.
Lemma 2.1 implies that subsequences  and
and  are eventually monotone.
are eventually monotone.
Since sequence  is bounded, then the subsequences
is bounded, then the subsequences  and
and  must converge. If the sequences
must converge. If the sequences  and
and  would converge to finite numbers, then the solution of (1.1) would converge to the period-two solution, which is impossible by Lemma 2.2. Thus at least one of the subsequences
would converge to finite numbers, then the solution of (1.1) would converge to the period-two solution, which is impossible by Lemma 2.2. Thus at least one of the subsequences  and
and  tends to
tends to  . Assume that
. Assume that  as
as  . In view of third equation of (4.25),
. In view of third equation of (4.25),  and in view of first equation of (4.25),
and in view of first equation of (4.25),  which by fourth equation of (4.25) implies that
which by fourth equation of (4.25) implies that  as
as  .
.
Now, we prove the case when  and
and 
In this case System (1.1) becomes

The map  associated to System (4.26) is given by
associated to System (4.26) is given by

Equilibrium curves  and
and  can be given explicitly as the following functions of
can be given explicitly as the following functions of 

It is obvious that these two curves do not intersect, which means that System (4.26) does not possess an equilibrium point.
Similarly, as in the proof of Theorem 4.3, for all points  the following holds:
the following holds:

Indeed,

Now, we have

The last inequality is equivalent to

which always holds.
Monotonicity of  implies
implies

Set  Then the sequence
Then the sequence  is increasing and the sequence
is increasing and the sequence  is decreasing. Since
is decreasing. Since  is decreasing and
is decreasing and  then it has to converge. If
then it has to converge. If  converges, then
converges, then  has to converge to the equilibrium, which is impossible. This implies that
has to converge to the equilibrium, which is impossible. This implies that  The second equation of System (4.26) implies that
The second equation of System (4.26) implies that 
Now, take any point  Then there exists point
Then there exists point  such that
such that

Monotonicity of  implies
implies

Set

Then, we have

Since

we conclude, using the inequalities (4.37), that

Similarly, we can prove the case 
References
Camouzis E, Kulenović MRS, Ladas G, Merino O: Rational systems in the plane. Journal of Difference Equations and Applications 2009,15(3):303-323. 10.1080/10236190802125264
Kulenović MRS, Merino O: Global bifurcation for discrete competitive systems in the plane. Discrete and Continuous Dynamical Systems. Series B 2009,12(1):133-149.
Kulenović MRS, Merino O: Invariant manifolds for competitive discrete systems in the plane. to appear in International Journal of Bifurcation and Chaos, http://arxiv.org/abs/0905.1772v1 to appear in International Journal of Bifurcation and Chaos,
Burgić Dž, Kalabušić S, Kulenović MRS: Nonhyperbolic dynamics for competitive systems in the plane and global period-doubling bifurcations. Advances in Dynamical Systems and Applications 2008,3(2):229-249.
Burgić Dž, Kulenović MRS, Nurkanović M: Global dynamics of a rational system of difference equations in the plane. Communications on Applied Nonlinear Analysis 2008,15(1):71-84.
Clark D, Kulenović MRS: A coupled system of rational difference equations. Computers & Mathematics with Applications 2002,43(6-7):849-867. 10.1016/S0898-1221(01)00326-1
Clark D, Kulenović MRS, Selgrade JF: Global asymptotic behavior of a two-dimensional difference equation modelling competition. Nonlinear Analysis. Theory, Methods & Applications 2003,52(7):1765-1776. 10.1016/S0362-546X(02)00294-8
Franke JE, Yakubu A-A: Mutual exclusion versus coexistence for discrete competitive systems. Journal of Mathematical Biology 1991,30(2):161-168. 10.1007/BF00160333
Franke JE, Yakubu A-A: Geometry of exclusion principles in discrete systems. Journal of Mathematical Analysis and Applications 1992,168(2):385-400. 10.1016/0022-247X(92)90167-C
Garić-Demirović M, Kulenović MRS, Nurkanović M: Global behavior of four competitive rational systems of difference equations in the plane. Discrete Dynamics in Nature and Society 2009, 2009:-34.
Hirsch MW, Smith H: Monotone dynamical systems. In Handbook of Differential Equations: Ordinary Differential Equations. Vol. II. Elsevier, Amsterdam, The Netherlands; 2005:239-357.
Kulenović MRS, Merino O: Competitive-exclusion versus competitive-coexistence for systems in the plane. Discrete and Continuous Dynamical Systems. Series B 2006,6(5):1141-1156.
Kulenović MRS, Nurkanović M: Asymptotic behavior of a system of linear fractional difference equations. Journal of Inequalities and Applications 2005, (2):127-143.
Kulenović MRS, Nurkanović M: Asymptotic behavior of a competitive system of linear fractional difference equations. Advances in Difference Equations 2006, 2006:-13.
Smith HL: Invariant curves for mappings. SIAM Journal on Mathematical Analysis 1986,17(5):1053-1067. 10.1137/0517075
Smith HL: Periodic competitive differential equations and the discrete dynamics of competitive maps. Journal of Differential Equations 1986,64(2):165-194. 10.1016/0022-0396(86)90086-0
Smith HL: Periodic solutions of periodic competitive and cooperative systems. SIAM Journal on Mathematical Analysis 1986,17(6):1289-1318. 10.1137/0517091
Smith HL: Planar competitive and cooperative difference equations. Journal of Difference Equations and Applications 1998,3(5-6):335-357. 10.1080/10236199708808108
Smith HL: Non-monotone systems decomposable into monotone systems with negative feedback. Journal of Differential Equations 2006, 53: 747-758.
de Mottoni P, Schiaffino A: Competition systems with periodic coefficients: a geometric approach. Journal of Mathematical Biology 1981,11(3):319-335. 10.1007/BF00276900
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kalabušić, S., Kulenović, M.R.S. & Pilav, E. Global Dynamics of a Competitive System of Rational Difference Equations in the Plane. Adv Differ Equ 2009, 132802 (2010). https://doi.org/10.1155/2009/132802
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/132802
 has a
has a  extension to a neighborhood of
extension to a neighborhood of  .
. at
at  has real eigenvalues
has real eigenvalues  ,
,  such that
such that  , where
, where  , and the eigenspace
, and the eigenspace  associated with
associated with  is not a coordinate axis.
is not a coordinate axis. is invariant, and
is invariant, and  as
as  for every
for every  .
. is invariant, and
is invariant, and  as
as  for every
for every  .
. there exists
there exists  such that
such that  for
for  .
. there exists
there exists  such that
such that  for
for  .
. and Period-Two Solution
and Period-Two Solution

 then
then  and
and 
 and
and  then
then  and
and 
 and
and  then
then  and
and 
 and
and  then
then  and
and 
 then
then 
 and
and  then
then 
 and
and  then
then 
 then
then  and
and 
 then
then  and
and 
 then
then 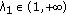 and
and 
 then
then  and
and 