- Research Article
- Open access
- Published:
The Existence of Periodic Solutions for Non-Autonomous Differential Delay Equations via Minimax Methods
Advances in Difference Equations volume 2009, Article number: 137084 (2009)
Abstract
By using variational methods directly, we establish the existence of periodic solutions for a class of nonautonomous differential delay equations which are superlinear both at zero and at infinity.
1. Introduction and Main Result
Many equations arising in nonlinear population growth models [1], communication systems [2], and even in ecology [3] can be written as the following differential delay equation:

where  is odd and
is odd and  is parameter. Since Jone's work in [4], there has been a great deal of research on problems of existence, multiplicity, stability, bifurcation, uniqueness, density of periodic solutions to (1.1) by applying various approaches. See [2, 4–23]. But most of those results concern scalar equations (1.1) and generally slowly oscillating periodic solutions. A periodic solution
is parameter. Since Jone's work in [4], there has been a great deal of research on problems of existence, multiplicity, stability, bifurcation, uniqueness, density of periodic solutions to (1.1) by applying various approaches. See [2, 4–23]. But most of those results concern scalar equations (1.1) and generally slowly oscillating periodic solutions. A periodic solution  of (1.1) is called a "slowly oscillating periodic solution" if there exist numbers
of (1.1) is called a "slowly oscillating periodic solution" if there exist numbers  and
and  such that
such that  for
for  ,
,  for
for  and
and  for all
for all  .
.
In a recent paper [17], Guo and Yu applied variational methods directly to study the following vector equation:

where  is odd and
is odd and  is a given constant. By using the pseudo index theory in [24], they established the existence and multiplicity of periodic solutions of (1.2) with
is a given constant. By using the pseudo index theory in [24], they established the existence and multiplicity of periodic solutions of (1.2) with  satisfying the following asymptotically linear conditions both at zero and at infinity:
satisfying the following asymptotically linear conditions both at zero and at infinity:

where  and
and  are symmetric
are symmetric  constant matrices. Before Guo and Yu's work, many authors generally first use the reduction technique introduced by Kaplan and Yorke in [7] to reduce the search for periodic solutions of (1.2) with
constant matrices. Before Guo and Yu's work, many authors generally first use the reduction technique introduced by Kaplan and Yorke in [7] to reduce the search for periodic solutions of (1.2) with  and its similar ones to the problem of finding periodic solutions for a related system of ordinary differential equations. Then variational method was applied to study the related systems and the existence of periodic solutions of the equations is obtained.
and its similar ones to the problem of finding periodic solutions for a related system of ordinary differential equations. Then variational method was applied to study the related systems and the existence of periodic solutions of the equations is obtained.
The previous papers concern mainly autonomous differential delay equations. In this paper, we use minimax methods directly to study the following nonautonomous differential-delay equation:

where  is odd with respect to
is odd with respect to  and satisfies the following superlinear conditions both at zero and at infinity
and satisfies the following superlinear conditions both at zero and at infinity

When (1.2) satisfies (1.3), we can apply the twist condition between the zero and at infinity for  to establish the existence of periodic solutions of (1.2). Under the superlinear conditions (1.5), there is no twist condition for
to establish the existence of periodic solutions of (1.2). Under the superlinear conditions (1.5), there is no twist condition for  , which brings difficulty to the study of the existence of periodic solutions of (1.4). But we can use minimax methods to consider the problem without twist condition for
, which brings difficulty to the study of the existence of periodic solutions of (1.4). But we can use minimax methods to consider the problem without twist condition for  .
.
Throughout this paper, we assume that the following conditions hold.
-
(H1)
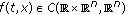 is odd with respect to
is odd with respect to  and
and 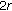 -periodic with respect to
-periodic with respect to  .
. -
(H2)
write
 . There exist constants
. There exist constants 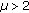 and
and 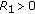 such that
such that (1.6)
(1.6) with
with  and
and  .
. -
(H3)
there exist constants
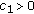 ,
, 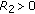 and
and 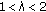 such that
such that (1.7)
(1.7)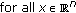 with
with  and
and 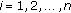 .
.
Then our main result can be read as follows.
Theorem 1.1.
Suppose that  satisfies (1.5) and the conditions
satisfies (1.5) and the conditions  hold. Then (1.4) possesses a nontrivial
hold. Then (1.4) possesses a nontrivial  -periodic solution.
-periodic solution.
Remark 1.2.
We shall use a minimax theorem in critical point theory in [25] to prove our main result. The ideas come from [25–27]. Theorem 1.1 will be proved in Section 2.
2. Proof of the Main Result
First of all in this section, we introduce a minimax theorem which will be used in our discussion. Let  be a Hilbert space with
be a Hilbert space with  . Let
. Let  be the projections of
be the projections of  onto
onto  and
and  , respectively.
, respectively.
Write

where  is compact.
is compact.
Definition 2.1.
Let  and
and  be boundary. One calls
be boundary. One calls  and
and  link if whenever
link if whenever  and
and  for all
for all  , then
, then  .
.
Definition 2.2.
A functional  satisfies
satisfies  condition, if every sequence that
condition, if every sequence that  ,
,  and
and  being bounded, possesses a convergent subsequence.
being bounded, possesses a convergent subsequence.
Then [25, Theorem  ] can be stated as follows.
] can be stated as follows.
Theorem 2 A.
Let  be a real Hilbert space with
be a real Hilbert space with  ,
,  and inner product
and inner product  . Suppose
. Suppose  satisfies
satisfies  condition,
condition,
 , where
, where  and
and  is bounded and selfadjoint,
is bounded and selfadjoint,  ,
,
 is compact, and
is compact, and
there exists a subspace  and sets
and sets  ,
,  and constants
and constants  such that
such that
 and
and  ,
,
 is bounded and
is bounded and  ,
,
 and
and  link.
link.
Then  possesses a critical value
possesses a critical value  .
.
Let

Then  and
and  , where
, where  denotes the gradient of
denotes the gradient of  with respect to
with respect to  . We have the following lemma.
. We have the following lemma.
Lemma 2.3.
Under the conditions of Theorem 1.1, the function  satisfies the following.
satisfies the following.
-
(i)
 is 2
is 2 -periodic with respect to
-periodic with respect to  and
and 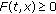 for all
for all 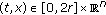 ,
, -
(ii)
 (2.3)
(2.3) (2.4)
(2.4) -
(iii)
There exist constants
 ,
,  and
and  such that for all
such that for all 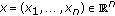 with
with  and
and  ,
,  , and
, and 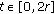
 (2.5)
(2.5)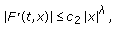 (2.6)
(2.6)where
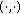 denotes the inner product in
denotes the inner product in  .
.
Proof.
The definition of  implies (i) directly. We prove case (ii) and case (iii).
implies (i) directly. We prove case (ii) and case (iii).
Case (ii). Let

Then  and
and  or
or  is equivalent to
is equivalent to  or
or  , respectively.
, respectively.
From (1.5) and L'Hospital rules, we have (2.3) by a direct computation.
Case (iii). By (H2), we have a constant  such that
such that  for
for  with
with  .
.
Now we prove  for
for  with
with  , that is,
, that is,

Firstly, it follows from  that
that  .
.
Now we show  . Let
. Let  ,
,  . By
. By  ,
,  , that is,
, that is,  . Then
. Then

By reducing method, we have

Thus, the inequality  for
for  holds.
holds.
Take  and
and  . Then (2.5) and (2.6) hold with
. Then (2.5) and (2.6) hold with  and
and  .
.
Below we will construct a variational functional of (1.4) defined on a suitable Hilbert space such that finding  -periodic solutions of (1.4) is equivalent to seeking critical points of the functional.
-periodic solutions of (1.4) is equivalent to seeking critical points of the functional.
Firstly, we make the change of variable

Then (1.4) can be changed to

where  is
is  -periodic with respect to
-periodic with respect to  . Therefore we only seek
. Therefore we only seek  -periodic solution of (2.12) which corresponds to the
-periodic solution of (2.12) which corresponds to the  -periodic solution of (1.4).
-periodic solution of (1.4).
We work in the Sobolev space  . The simplest way to introduce this space seems as follows. Every function
. The simplest way to introduce this space seems as follows. Every function  has a Fourier expansion:
has a Fourier expansion:

where  are
are  -vectors.
-vectors.  is the set of such functions that
is the set of such functions that

With this norm  ,
,  is a Hilbert space induced by the inner product
is a Hilbert space induced by the inner product  defined by
defined by

where 
We define a functional  by
by

By Riesz representation theorem, H identifies with its dual space H*. Then we define an operator A:H→H*=H by extending the bilinear form:

It is not difficult to see that  is a bounded linear operator on
is a bounded linear operator on  and
and  .
.
Define a mapping  as
as

Then the functional  can be rewritten as
can be rewritten as

According to a standard argument in [24], one has for any  ,
,

Moreover according to [28],  is a compact operator defined by
is a compact operator defined by

Our aim is to reduce the existence of periodic solutions of (2.12) to the existence of critical points of  . For this we introduce a shift operator
. For this we introduce a shift operator  defined by
defined by

It is easy to compute that  is bounded and linear. Moreover
is bounded and linear. Moreover  is isometric, that is,
is isometric, that is,  and
and  , where
, where  denotes the identity mapping on
denotes the identity mapping on  .
.
Write

Lemma 2.4.
Critical points of  over
over  are critical points of
are critical points of  on
on  , where
, where  is the restriction of
is the restriction of  over
over  .
.
Proof.
Note that any  is
is  -periodic and
-periodic and  is odd with respect to
is odd with respect to  . It is enough for us to prove
. It is enough for us to prove  for any
for any  and
and  being a critical point of
being a critical point of  in
in  .
.
For any  , we have
, we have

This yields  , that is,
, that is,  .
.
Suppose that  is a critical point of
is a critical point of  in
in  . We only need to show that
. We only need to show that  for any
for any  . Writing
. Writing  with
with  and noting
and noting  , one has
, one has

The proof is complete.
Remark 2.5.
By Lemma 2.4, we only need to find critical points of  over
over  . Therefore in the following
. Therefore in the following  will be assumed on
will be assumed on  .
.
For  ,
,  yields that
yields that  , where
, where  is in the Fourier expansion of
is in the Fourier expansion of  . Thus
. Thus  . Moreover for any
. Moreover for any  ,
,

Hence  is self-adjoint on
is self-adjoint on  .
.
Let  and
and  denote the positive definite and negative definite subspace of
denote the positive definite and negative definite subspace of  in
in  , respectively. Then
, respectively. Then  . Letting
. Letting  ,
,  , we see that
, we see that  of Theorem A holds. Since
of Theorem A holds. Since  is compact,
is compact,  of Theorem A holds. Now we establish
of Theorem A holds. Now we establish  of Theorem A by the following three lemmas.
of Theorem A by the following three lemmas.
Lemma 2.6.
Under the assumptions of Theorem 1.1,  of
of  holds for
holds for  .
.
Proof.
From the assumptions of Theorem 1.1 and Lemma 2.3, one has

By (2.3), for any  , there is a
, there is a  such that
such that

Therefore, there is an  such that
such that

Since  is compactly embedded in
is compactly embedded in  for all
for all  and by (2.29), we have
and by (2.29), we have

Consequently, for  ,
,

Choose  and
and  so that
so that  . Then for any
. Then for any  ,
,

Thus  satisfies
satisfies  of
of  with
with  and
and  .
.
Lemma 2.7.
Under the assumptions of Theorem 1.1,  satisfies
satisfies  of
of  .
.
Proof.
Set  and let
and let

where  is free for the moment.
is free for the moment.
Let  . Write
. Write

Case (1). If  with
with  , one has
, one has

Case (2). If  , we have
, we have

That is

Denote  . By appendix, there exists
. By appendix, there exists  such that
such that  ,
,

Now for  , set
, set  . By (2.4), for a constant
. By (2.4), for a constant  , there is an
, there is an  such that
such that

Choosing  , for
, for  ,
,

For  , we have
, we have

Henceforth,  for any
for any  and
and  , that is,
, that is,  . Then
. Then  of
of  holds.
holds.
Lemma 2.8.
 and
and  link.
link.
Proof.
Suppose  and
and  for all
for all  . Then we claim that for each
. Then we claim that for each  , there is a
, there is a  such that
such that  , that is,
, that is,

where  is a projection. Define
is a projection. Define

as follows:

It is easy to see that

However,

According to topological degree theory in [29], we have

since  . Therefore
. Therefore  and
and  link.
link.
Now it remains to verify that  satisfies
satisfies  -condition.
-condition.
Lemma 2.9.
Under the assumptions of Theorem 1.1,  satisfies
satisfies  -condition.
-condition.
Proof.
Suppose that

We first show that  is bounded. If
is bounded. If  is not bounded, then by passing to a subsequence if necessary, let
is not bounded, then by passing to a subsequence if necessary, let  as
as  .
.
By (2.4), there exists a constant  such that
such that  as
as  . By (2.5), one has
. By (2.5), one has

This yields

Write  . By (2.6), there is a constant
. By (2.6), there is a constant  such that
such that

Therefore,

This inequality and (2.50) imply that

as  , since
, since  .
.
Denote  . We have
. We have

where  is a constant independent of
is a constant independent of  .
.
By the above inequality, one has

as  . This yields
. This yields

Similarly, we have

Thus it follows from (2.56) and (2.57) that

which is a contradiction. Hence  is bounded.
is bounded.
Below we show that  has a convergent subsequence. Notice that
has a convergent subsequence. Notice that  and
and  is compact. Since
is compact. Since  is bounded, we may suppose that
is bounded, we may suppose that

Since  has continuous inverse
has continuous inverse  in
in  , it follows from
, it follows from

that

Henceforth  has a convergent subsequence.
has a convergent subsequence.
Now we are ready to prove Theorem 1.1.
Proof of Theorem 1.1.
It is obviously that Theorem 1.1 holds from Lemmas 2.3, 2.4, 2.6, 2.7, 2.8, and 2.9 and Theorem A.
References
Cunningham WJ: A nonlinear differential-difference equation of growth. Proceedings of the National Academy of Sciences of the United States of America 1954,40(4):708-713.
Furumochi T: Existence of periodic solutions of one-dimensional differential-delay equations. The Tôhoku Mathematical Journal 1978,30(1):13-35.
May R: Stablity and Complexity in Model Ecosystems. Princeton University Press, Princeton, NJ, USA; 1973.
Jones GS:The existence of periodic solutions of

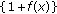 . Journal of Mathematical Analysis and Applications 1962,5(3):435-450. 10.1016/0022-247X(62)90017-3
. Journal of Mathematical Analysis and Applications 1962,5(3):435-450. 10.1016/0022-247X(62)90017-3Chow S-N, Walther H-O:Characteristic multipliers and stability of symmetric periodic solutions of
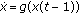 . Transactions of the American Mathematical Society 1988,307(1):127-142.
. Transactions of the American Mathematical Society 1988,307(1):127-142.Herz AV:Solutions of
 approach the Kaplan-Yorke orbits for odd sigmoid
approach the Kaplan-Yorke orbits for odd sigmoid 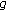 . Journal of Differential Equations 1995,118(1):36-53. 10.1006/jdeq.1995.1066
. Journal of Differential Equations 1995,118(1):36-53. 10.1006/jdeq.1995.1066Kaplan J, Yorke J: Ordinary differential equations which yield periodic solutions of differential delay equations. Journal of Mathematical Analysis and Applications 1974,48(2):317-324. 10.1016/0022-247X(74)90162-0
Kaplan J, Yorke J: On the stability of a periodic solution of a differential delay equation. SIAM Journal on Mathematical Analysis 1975,6(2):268-282. 10.1137/0506028
Yorke J: Asymptotic stability for one dimensional differential-delay equations. Journal of Differential Equations 1970,7(1):189-202. 10.1016/0022-0396(70)90132-4
Chapin S: Periodic solutions of differential-delay equations with more than one delay. The Rocky Mountain Journal of Mathematics 1987,17(3):555-572. 10.1216/RMJ-1987-17-3-555
Walther H-O:Density of slowly oscillating solutions of
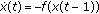 . Journal of Mathematical Analysis and Applications 1981,79(1):127-140. 10.1016/0022-247X(81)90014-7
. Journal of Mathematical Analysis and Applications 1981,79(1):127-140. 10.1016/0022-247X(81)90014-7Nussbaum RD: Periodic solutions of special differential equations: an example in nonlinear functional analysis. Proceedings of the Royal Society of Edinburgh. Section A 1978,81(1-2):131-151. 10.1017/S0308210500010490
Nussbaum RD: A Hopf global bifurcation theorem for retarded functional differential equations. Transactions of the American Mathematical Society 1978,238(1):139-164.
Nussbaum RD:Uniqueness and nonuniqueness for periodic solutions of
 . Journal of Differential Equations 1979,34(1):25-54. 10.1016/0022-0396(79)90016-0
. Journal of Differential Equations 1979,34(1):25-54. 10.1016/0022-0396(79)90016-0Li J, He X-Z, Liu Z: Hamiltonian symmetric groups and multiple periodic solutions of differential delay equations. Nonlinear Analysis: Theory, Methods & Applications 1999,35(4):457-474. 10.1016/S0362-546X(97)00623-8
Li J, He X-Z: Multiple periodic solutions of differential delay equations created by asymptotically linear Hamiltonian systems. Nonlinear Analysis: Theory, Methods & Applications 1998,31(1-2):45-54. 10.1016/S0362-546X(96)00058-2
Guo Z, Yu J: Multiplicity results for periodic solutions to delay differential equations via critical point theory. Journal of Differential Equations 2005,218(1):15-35. 10.1016/j.jde.2005.08.007
Llibre J, Tarţa A-A: Periodic solutions of delay equations with three delays via bi-Hamiltonian systems. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2433-2441. 10.1016/j.na.2005.08.023
Jekel S, Johnston C: A Hamiltonian with periodic orbits having several delays. Journal of Differential Equations 2006,222(2):425-438. 10.1016/j.jde.2005.08.013
Fei G: Multiple periodic solutions of differential delay equations via Hamiltonian systems. I. Nonlinear Analysis: Theory, Methods & Applications 2006,65(1):25-39. 10.1016/j.na.2005.06.011
Fei G: Multiple periodic solutions of differential delay equations via Hamiltonian systems. II. Nonlinear Analysis: Theory, Methods & Applications 2006,65(1):40-58. 10.1016/j.na.2005.06.012
Han MA: Bifurcations of periodic solutions of delay differential equations. Journal of Differential Equations 2003,189(2):396-411. 10.1016/S0022-0396(02)00106-7
Dormayer P:The stability of special symmetric solutions of
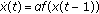 with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701-715. 10.1016/0362-546X(90)90045-I
with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701-715. 10.1016/0362-546X(90)90045-IBenci V: On critical point theory for indefinite functionals in the presence of symmetries. Transactions of American Mathematical Society 1982,247(2):533-572.
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. American Mathematical Society, Providence, RI, USA; 1986.
Fei G: On periodic solutions of superquadratic Hamiltonian systems. Electronic Journal of Differential Equations 2002, 8: 1-12.
Chang KC: Critical Point Theory and Applications. Shanghai Science & Technology Press, Beijing, China; 1986.
Long Y, Zehnder E: Morse-theory for forced oscillations of asymptotically linear Hamiltonian systems. In Stochastic Processes in Physics and Geometry. World Scientific, Singapore; 1990:528-563.
Mawhin J, Willem M: Critical point theory and Hamiltonian systems. In Applied Mathematical Sciences. Volume 74. Springer, Berlin, Germany; 1989.
Acknowledgments
This work is supported by the Specialized Research Fund for the Doctoral Program of Higher Education for New Teachers and the Science Research Foundation of Nanjing University of Information Science and Technology (20070049).
Author information
Authors and Affiliations
Corresponding author
Appendix
The purpose of this appendix is to prove the following lemma. The main idea of the proof comes from [26]. Lemma A.1. There exists  such that,
such that,  ,
,

 , there exists
, there exists  such that
such that
 . Notice that dim
. Notice that dim and
and  . In the sense of subsequence, we have
. In the sense of subsequence, we have

 , in the sense of subsequence
, in the sense of subsequence  as
as  . Thus in the sense of subsequence,
. Thus in the sense of subsequence,
 in
in  , that is,
, that is,
 . Therefore,
. Therefore,  . Then there exist
. Then there exist  such that
such that
 , we must have
, we must have
 ,
,  . We get a contradiction. Thus (A.7) holds. Let
. We get a contradiction. Thus (A.7) holds. Let  ,
,  , and
, and  . By (A.2), we have
. By (A.2), we have
 be large enough such that
be large enough such that  and
and  . Then we have
. Then we have












Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cheng, R. The Existence of Periodic Solutions for Non-Autonomous Differential Delay Equations via Minimax Methods. Adv Differ Equ 2009, 137084 (2009). https://doi.org/10.1155/2009/137084
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/137084
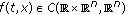 is odd with respect to
is odd with respect to  and
and 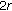 -periodic with respect to
-periodic with respect to  .
. . There exist constants
. There exist constants 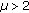 and
and 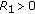 such that
such that
 with
with  and
and  .
.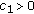 ,
, 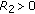 and
and 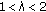 such that
such that
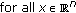 with
with  and
and 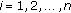 .
. is 2
is 2 -periodic with respect to
-periodic with respect to  and
and 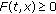 for all
for all 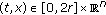 ,
,

 ,
,  and
and  such that for all
such that for all 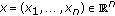 with
with  and
and  ,
,  , and
, and 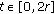

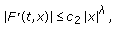
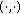 denotes the inner product in
denotes the inner product in  .
.
 . Journal of Mathematical Analysis and Applications 1962,5(3):435-450. 10.1016/0022-247X(62)90017-3
. Journal of Mathematical Analysis and Applications 1962,5(3):435-450. 10.1016/0022-247X(62)90017-3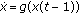 . Transactions of the American Mathematical Society 1988,307(1):127-142.
. Transactions of the American Mathematical Society 1988,307(1):127-142. approach the Kaplan-Yorke orbits for odd sigmoid
approach the Kaplan-Yorke orbits for odd sigmoid 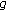 . Journal of Differential Equations 1995,118(1):36-53. 10.1006/jdeq.1995.1066
. Journal of Differential Equations 1995,118(1):36-53. 10.1006/jdeq.1995.1066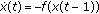 . Journal of Mathematical Analysis and Applications 1981,79(1):127-140. 10.1016/0022-247X(81)90014-7
. Journal of Mathematical Analysis and Applications 1981,79(1):127-140. 10.1016/0022-247X(81)90014-7 . Journal of Differential Equations 1979,34(1):25-54. 10.1016/0022-0396(79)90016-0
. Journal of Differential Equations 1979,34(1):25-54. 10.1016/0022-0396(79)90016-0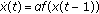 with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701-715. 10.1016/0362-546X(90)90045-I
with small amplitudes. Nonlinear Analysis: Theory, Methods & Applications 1990,14(8):701-715. 10.1016/0362-546X(90)90045-I