- Research Article
- Open access
- Published:
Existence of Periodic Solutions for a Delayed Ratio-Dependent Three-Species Predator-Prey Diffusion System on Time Scales
Advances in Difference Equations volume 2009, Article number: 141589 (2009)
Abstract
This paper investigates the existence of periodic solutions of a ratio-dependent predator-prey diffusion system with Michaelis-Menten functional responses and time delays in a two-patch environment on time scales. By using a continuation theorem based on coincidence degree theory, we obtain suffcient criteria for the existence of periodic solutions for the system. Moreover, when the time scale  is chosen as
is chosen as  or
or  , the existence of the periodic solutions of the corresponding continuous and discrete models follows. Therefore, the methods are unified to provide the existence of the desired solutions for the continuous differential equations and discrete difference equations.
, the existence of the periodic solutions of the corresponding continuous and discrete models follows. Therefore, the methods are unified to provide the existence of the desired solutions for the continuous differential equations and discrete difference equations.
1. Introduction
The traditional predator-prey model has received great attention from both theoretical and mathematical biologists and has been studied extensively (e.g., see [1–4] and references therein). Based on growing biological and physiological evidences, some biologists have argued that in many situations, especially when predators have to search for food (and therefore, have to share or compete for food), the functional response in a prey-predator model should be ratio-dependent, which can be roughly stated as that the per capita predator growth rate should be a function of the ratio of prey to predator abundance. Starting from this argument and the traditional prey-dependent-only mode, Arditi and Ginzburg [5] first proposed the following ratio-dependent predator-prey model:

which incorporates mutual interference by predators, where  is a Michaelis-Menten type functional response function. Equation (1.1) has been studied by many authors and seen great progress (e.g., see [6–11]).
is a Michaelis-Menten type functional response function. Equation (1.1) has been studied by many authors and seen great progress (e.g., see [6–11]).
Xu and Chen [11] studied a delayed two-predator-one-prey model in two patches which is described by the following differential equations:

In view of periodicity of the actual environment, Huo and Li [12] investigated a more general delayed ratio-dependent predator-prey model with periodic coefficients of the form

In order to consider periodic variations of the environment and the density regulation of the predators though taking into account delay effect and diffusion between patches, more realistic and interesting models of population interactions should take into account comprehensively other than one or two aspects. On the other hand, in order to unify the study of differential and difference equations, people have done a lot of research about dynamic equations on time scales. The principle aim of this paper is to systematically unify the existence of periodic solutions for a delayed ratio-dependent predator-prey system with functional response and diffusion modeled by ordinary differential equations and their discrete analogues in form of difference equations and to extend these results to more general time scales. The approach is based on Gaines and Mawhin's continuation theorem of coincidence degree theory, which has been widely applied to deal with the existence of periodic solutions of differential equations and difference equations.
Therefore, it is interesting and important to study the following model on time scales  :
:

with the initial conditions

where  . In (1.4),
. In (1.4),  represents the prey population in the
represents the prey population in the  th patch
th patch  , and
, and  represents the predator population.
represents the predator population.  is the prey for
is the prey for  , and
, and  is the prey for
is the prey for  so that they form a food chain.
so that they form a food chain.  denotes the dispersal rate of the prey in the
denotes the dispersal rate of the prey in the  th patch
th patch  . For the sake of generality and convenience, we always make the following fundamental assumptions for system (1.4):
. For the sake of generality and convenience, we always make the following fundamental assumptions for system (1.4):
-
(H)
 are all rd-continuous positive periodic functions with period
are all rd-continuous positive periodic functions with period  ;
; 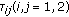 are nonnegative constants.
are nonnegative constants.
In (1.4), set  . If
. If  , then (1.4) reduces to the ratio-dependent predator-prey diffusive system of three species with time delays governed by the ordinary differential equations
, then (1.4) reduces to the ratio-dependent predator-prey diffusive system of three species with time delays governed by the ordinary differential equations

If  , then (1.4) is reformulated as
, then (1.4) is reformulated as

which is the discrete time ratio-dependent predator-prey diffusive system of three species with time delays and is also a discrete analogue of (1.6).
2. Preliminaries
A time scale  is an arbitrary nonempty closed subset of the real numbers
is an arbitrary nonempty closed subset of the real numbers  . Throughout the paper, we assume the time scale
. Throughout the paper, we assume the time scale  is unbounded above and below, such as
is unbounded above and below, such as  and
and  . The following definitions and lemmas can be found in [13].
. The following definitions and lemmas can be found in [13].
Definition 2.1.
The forward jump operator  , the backward jump operator
, the backward jump operator  , and the graininess
, and the graininess  are defined, respectively, by
are defined, respectively, by

If  , then
, then  is called right-dense (otherwise: right-scattered), and if
is called right-dense (otherwise: right-scattered), and if  , then
, then  is called left-dense (otherwise: left-scattered).
is called left-dense (otherwise: left-scattered).
If  has a left-scattered maximum
has a left-scattered maximum  , then
, then  ; otherwise
; otherwise  . If
. If  has a right-scattered minimum
has a right-scattered minimum  , then
, then  ; otherwise
; otherwise  .
.
Definition 2.2.
Assume  is a function and let
is a function and let  . Then one defines
. Then one defines  to be the number (provided it exists) with the property that given any
to be the number (provided it exists) with the property that given any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

In this case,  is called the delta (or Hilger) derivative of
is called the delta (or Hilger) derivative of  at
at  . Moreover,
. Moreover,  is said to be delta or Hilger differentiable on
is said to be delta or Hilger differentiable on  if
if  exists for all
exists for all  . A function
. A function  is called an antiderivative of
is called an antiderivative of  provided
provided  for all
for all  . Then one defines
. Then one defines

Definition 2.3.
A function  is said to be rd-continuous if it is continuous at right-dense points in
is said to be rd-continuous if it is continuous at right-dense points in  and its left-sided limits exists (finite) at left-dense points in
and its left-sided limits exists (finite) at left-dense points in  . The set of rd-continuous functions
. The set of rd-continuous functions  will be denoted by
will be denoted by  .
.
Definition 2.4.
If  ,
,  , and
, and  is rd-continuous on
is rd-continuous on  , then one defines the improper integral by
, then one defines the improper integral by

provided this limit exists, and one says that the improper integral converges in this case.
Definition 2.5 (see [14]).
One says that a time scale  is periodic if there exists
is periodic if there exists  such that if
such that if  , then
, then  . For
. For  , the smallest positive
, the smallest positive  is called the period of the time scale.
is called the period of the time scale.
Definition 2.6 (see [14]).
Let  be a periodic time scale with period
be a periodic time scale with period  . One says that the function
. One says that the function  is periodic with period
is periodic with period  if there exists a natural number
if there exists a natural number  such that
such that  ,
,  for all
for all  and
and  is the smallest number such that
is the smallest number such that  .
.
If  , one says that
, one says that  is periodic with period
is periodic with period  if
if  is the smallest positive number such that
is the smallest positive number such that  for all
for all  .
.
Lemma 2.7.
Every rd-continuous function has an antiderivative.
Lemma 2.8.
Every continuous function is rd-continuous.
Lemma 2.9.
If  and
and  , then
, then
-
(a)
 ;
; -
(b)
if
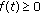 for all
for all 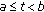 , then
, then  ;
; -
(c)
if
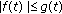 on
on 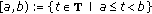 , then
, then  .
.
Lemma 2.10.
If  , then
, then  is nondecreasing.
is nondecreasing.
Notation.
To facilitate the discussion below, we now introduce some notation to be used throughout this paper. Let  be
be  -periodic, that is,
-periodic, that is,  implies
implies  ,
,

where  is an
is an  -periodic function, that is,
-periodic function, that is,  for all
for all  ,
,  .
.
Notation.
Let  be two Banach spaces, let
be two Banach spaces, let  be a linear mapping, and let
be a linear mapping, and let  be a continuous mapping. If
be a continuous mapping. If  is a Fredholm mapping of index zero and there exist continuous projectors
is a Fredholm mapping of index zero and there exist continuous projectors  and
and  such that
such that  ,
,  , then the restriction
, then the restriction  is invertible. Denote the inverse of that map by
is invertible. Denote the inverse of that map by  . If
. If  is an open bounded subset of
is an open bounded subset of  , the mapping
, the mapping  will be called
will be called  -compact on
-compact on  if
if  is bounded and
is bounded and  is compact. Since
is compact. Since  is isomorphic to
is isomorphic to  , there exists an isomorphism
, there exists an isomorphism  .
.
Lemma 2.11 (Continuation theorem [15]).
Let  be two Banach spaces, and let
be two Banach spaces, and let  be a Fredholm mapping of index zero. Assume that
be a Fredholm mapping of index zero. Assume that  is
is  -compact on
-compact on  with
with  is open bounded in
is open bounded in  . Furthermore assume the following:
. Furthermore assume the following:
-
(a)
for each
 ;
; -
(b)
for each
 ;
; -
(c)
 .
.
Then the operator equation  has at least one solution in
has at least one solution in  .
.
Lemma 2.12 (see [16]).
Let  . If
. If  is
is  -periodic, then
-periodic, then

3. Existence of Periodic Solutions
The fundamental theorem in this paper is stated as follows about the existence of an  -periodic solution.
-periodic solution.
Theorem 3.1.
Suppose that (H) holds. Furthermore assume the following:
-
(i)

-
(ii)
 ,
, -
(iii)
 ,
, -
(iv)
 ,
,
then the system (1.4) has at least one  -periodic solution.
-periodic solution.
Proof.
Consider vector equation

Define

where  is the Euclidean norm. Then
is the Euclidean norm. Then  and
and  are both Banach spaces with the above norm
are both Banach spaces with the above norm  . Let
. Let  . Then
. Then

and  . Since
. Since  is closed in
is closed in  , then
, then  is a Fredholm mapping of index zero. It is easy to show that
is a Fredholm mapping of index zero. It is easy to show that  are continuous projectors such that
are continuous projectors such that  . Furthermore, the generalized inverse (to
. Furthermore, the generalized inverse (to  )
)  exists and is given by
exists and is given by  , thus
, thus

Obviously,  are continuous. Since
are continuous. Since  is a Banach space, using the Arzela-Ascoli theorem, it is easy to show that
is a Banach space, using the Arzela-Ascoli theorem, it is easy to show that  is compact for any open bounded set
is compact for any open bounded set  . Moreover,
. Moreover,  is bounded, thus,
is bounded, thus,  is
is  -compact on
-compact on  for any open bounded set
for any open bounded set  . Corresponding to the operator equation
. Corresponding to the operator equation  , we have
, we have

Suppose that  is a solution of (3.5) for certain
is a solution of (3.5) for certain  . Integrating on both sides of (3.5) from
. Integrating on both sides of (3.5) from  to
to  with respect to
with respect to  , we have
, we have




It follows from (3.5) to (3.9) that




Multiplying (3.6) by  and integrating over
and integrating over  gives
gives

which yields

By using the inequality  , we have
, we have

Then

By using the inequality  , we derive from (3.17) that
, we derive from (3.17) that

Similarly, multiplying (3.7) by  and integrating over
and integrating over  , then synthesize the above, we obtain
, then synthesize the above, we obtain

It follows from (3.18) and (3.19) that

so, there exists a positive constant  such that
such that

which together with (3.19), there also exists a positive constant  such that
such that

This, together with (3.11), (3.12), and (3.21), leads to

Since  , there exist some points
, there exist some points  , such that
, such that

It follows from (3.21) and (3.22) that

From (3.8) and (3.9), we obtain that

This, together with (3.12), (3.13), and (3.26), deduces

From (3.6) and (3.24), we have

From (3.7) and (3.24), it yields that

Noticing that  , from (3.8) and (3.9), deduces
, from (3.8) and (3.9), deduces

There exist two points  such that
such that

Hence,

where  . Then, this, together with (3.12), (3.13), (3.23), (3.28), (3.29), and (3.32), deduces
. Then, this, together with (3.12), (3.13), (3.23), (3.28), (3.29), and (3.32), deduces

It follows from (3.27) to (3.33) that

From (3.34), we clearly know that  are independent of
are independent of  , and from the representation of
, and from the representation of  , it is easy to know that there exist points
, it is easy to know that there exist points  such that
such that  , where
, where

Take  , where
, where  is taken sufficiently large such that
is taken sufficiently large such that  , and such that each solution
, and such that each solution  of the system
of the system  satisfies
satisfies  if the system (3.35) has solutions. Now take
if the system (3.35) has solutions. Now take  . Then it is clear that
. Then it is clear that  verifies the requirement (a) of Lemma 2.11.
verifies the requirement (a) of Lemma 2.11.
When  ,
,  is a constant vector in
is a constant vector in  with
with  , from the definition of
, from the definition of  , we can naturally derive
, we can naturally derive  whether the system (3.35) has solutions or not. This shows that the condition (b) of Lemma 2.11 is satisfied.
whether the system (3.35) has solutions or not. This shows that the condition (b) of Lemma 2.11 is satisfied.
Finally, we will prove that the condition (c) of Lemma 2.11 is valid. Define the homotopy  by
by

where

where  is a parameter. From (3.37), it is easy to show that
is a parameter. From (3.37), it is easy to show that  . Moreover, one can easily show that the algebraic equation
. Moreover, one can easily show that the algebraic equation

has a unique positive solution  in
in  . Note that
. Note that  (identical mapping), since
(identical mapping), since  , according to the invariance property of homotopy, direct calculation produces
, according to the invariance property of homotopy, direct calculation produces

where  is the Brouwer degree. By now we have proved that
is the Brouwer degree. By now we have proved that  verifies all requirements of Lemma 2.11. Therefore, (1.4) has at least one
verifies all requirements of Lemma 2.11. Therefore, (1.4) has at least one  -periodic solution in
-periodic solution in  . The proof is complete.
. The proof is complete.
Corollary 3.2.
If the conditions in Theorem 3.1 hold, then both the corresponding continuous model (1.6) and the discrete model (1.7) have at least one  -periodic solution.
-periodic solution.
Remark 3.3.
If  and
and  in (1.6), then the system (1.6) reduces to the continuous ratio-dependence predator-prey diffusive system proposed in [17].
in (1.6), then the system (1.6) reduces to the continuous ratio-dependence predator-prey diffusive system proposed in [17].
Remark 3.4.
If we only consider the prey population in one-patch environment and ignore the dispersal process in the system (1.4), then the classical ratio-dependence two species predator-prey model in particular of (1.4) with Michaelis-Menten functional response and time delay on time scales

where  are positive
are positive  -periodic functions,
-periodic functions,  is nonnegative constant. It is easy to obtain the corresponding conclusions on time scales for the system (3.40).
is nonnegative constant. It is easy to obtain the corresponding conclusions on time scales for the system (3.40).
Corollary 3.5.
Suppose that (i)  , (ii)
, (ii)  hold, then (3.40) has at least one
hold, then (3.40) has at least one  -periodic solution.
-periodic solution.
Remark 3.6.
The result in Corollary 3.5 is same as those for the corresponding continuous and discrete systems.
References
Beretta E, Kuang Y: Convergence results in a well-known delayed predator-prey system. Journal of Mathematical Analysis and Applications 1996,204(3):840-853. 10.1006/jmaa.1996.0471
Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Dynamics, Mathematics and Its Applications. Volume 74. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992.
Kuang Y: Delay Differential Equations with Applications in Population Dynamics, Mathematics in Science and Engineering. Volume 191. Academic Press, Boston, Mass, USA; 1993:xii+398.
Kuang Y: Rich dynamics of Gause-type ratio-dependent predator-prey system. In Differential Equations with Applications to Biology (Halifax, NS, 1997), Fields Institute Communications. Volume 21. American Mathematical Society, Providence, RI, USA; 1999:325-337.
Arditi R, Ginzburg LR: Coupling in predator-prey dynamics: ratio-dependence. Journal of Theoretical Biology 1989,139(3):311-326. 10.1016/S0022-5193(89)80211-5
Fan M, Wang K: Periodicity in a delayed ratio-dependent predator-prey system. Journal of Mathematical Analysis and Applications 2001,262(1):179-190. 10.1006/jmaa.2001.7555
Fan M, Wang Q: Periodic solutions of a class of nonautonomous discrete time semi-ratio-dependent predator-prey systems. Discrete and Continuous Dynamical Systems. Series B 2004,4(3):563-574.
Hsu S-B, Hwang T-W, Kuang Y: Global analysis of the Michaelis-Menten-type ratio-dependent predator-prey system. Journal of Mathematical Biology 2001,42(6):489-506. 10.1007/s002850100079
Jost C, Arino O, Arditi R: About deterministic extinction in ratio-dependent predator-prey models. Bulletin of Mathematical Biology 1999,61(1):19-32. 10.1006/bulm.1998.0072
Xiao D, Ruan S: Multiple bifurcations in a delayed predator-prey system with nonmonotonic functional response. Journal of Differential Equations 2001,176(2):494-510. 10.1006/jdeq.2000.3982
Xu R, Chen L: Persistence and global stability for a three-species ratio-dependent predator-prey system with time delays in two-patch environments. Acta Mathematica Scientia. Series B 2002,22(4):533-541.
Huo H-F, Li W-T: Periodic solution of a delayed predator-prey system with Michaelis-Menten type functional response. Journal of Computational and Applied Mathematics 2004,166(2):453-463. 10.1016/j.cam.2003.08.042
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Kaufmann ER, Raffoul YN: Periodic solutions for a neutral nonlinear dynamical equation on a time scale. Journal of Mathematical Analysis and Applications 2006,319(1):315-325. 10.1016/j.jmaa.2006.01.063
Gaines RE, Mawhin JL: Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics. Volume 568. Springer, Berlin, Germany; 1977:i+262.
Bohner M, Fan M, Zhang J: Existence of periodic solutions in predator-prey and competition dynamic systems. Nonlinear Analysis: Real World Applications 2006,7(5):1193-1204. 10.1016/j.nonrwa.2005.11.002
Wen S, Chen S, Mei H: Positive periodic solution of a more realistic three-species Lotka-Volterra model with delay and density regulation. Chaos, Solitons and Fractals. In press
Acknowledgments
The author is very grateful to his supervisor Prof. M. Fan and the anonymous referees for their many valuable comments and suggestions which greatly improved the presentation of this paper. This work is supported by the Foundation for subjects development of Harbin University (no. HXK200716) and by the Foundation for Scientific Research Projects of Education Department of Hei-longjiang Province of China (no. 11513043).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Z. Existence of Periodic Solutions for a Delayed Ratio-Dependent Three-Species Predator-Prey Diffusion System on Time Scales. Adv Differ Equ 2009, 141589 (2009). https://doi.org/10.1155/2009/141589
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/141589
 are all rd-continuous positive periodic functions with period
are all rd-continuous positive periodic functions with period  ;
; 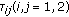 are nonnegative constants.
are nonnegative constants. ;
;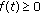 for all
for all 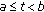 , then
, then  ;
;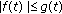 on
on 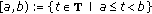 , then
, then  .
. ;
; ;
; .
.
 ,
, ,
, ,
,