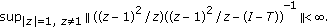- Research Article
- Open access
- Published:
Maximal Regularity of the Discrete Harmonic Oscillator Equation
Advances in Difference Equations volume 2009, Article number: 290625 (2009)
Abstract
We give a representation of the solution for the best approximation of the harmonic oscillator equation formulated in a general Banach space setting, and a characterization of  -maximal regularity—or well posedness—solely in terms of
-maximal regularity—or well posedness—solely in terms of  -boundedness properties of the resolvent operator involved in the equation.
-boundedness properties of the resolvent operator involved in the equation.
1. Introduction
In numerical integration of a differential equation, a standard approach is to replace it by a suitable difference equation whose solution can be obtained in a stable manner and without troubles from round off errors. However, often the qualitative properties of the solutions of the difference equation are quite different from the solutions of the corresponding differential equations.
For a given differential equation, a difference equation approximation is called best if the solution of the difference equation exactly coincides with solutions of the corresponding differential equation evaluated at a discrete sequence of points. Best approximations are not unique (cf. [1, Section 3.6]).
In the recent paper [2] (see also [1]), various discretizations of the harmonic oscillator equation  are compared. A best approximation is given by
are compared. A best approximation is given by

where  denotes the forward difference operator of the first order, that is, for each
denotes the forward difference operator of the first order, that is, for each  and
and  On the other hand, in the article [3], a characterization of
On the other hand, in the article [3], a characterization of  -maximal regularity for a discrete second-order equation in Banach spaces was studied, but without taking into account the best approximation character of the equation. From an applied perspective, the techniques used in [3] are interesting when applied to concrete difference equations, but additional difficulties appear, because among other things, we need to get explicit formulas for the solution of the equation to be studied.
-maximal regularity for a discrete second-order equation in Banach spaces was studied, but without taking into account the best approximation character of the equation. From an applied perspective, the techniques used in [3] are interesting when applied to concrete difference equations, but additional difficulties appear, because among other things, we need to get explicit formulas for the solution of the equation to be studied.
We study in this paper the discrete second-order equation

on complex Banach spaces, where  . Of course, in the finite-dimensional setting, (1.2) includes systems of linear difference equations, but the most interesting application concerns with partial difference equations. In fact, the homogeneous equation associated to (1.2) corresponds to the best discretization of the wave equation (cf. [1, Section 3.14]).
. Of course, in the finite-dimensional setting, (1.2) includes systems of linear difference equations, but the most interesting application concerns with partial difference equations. In fact, the homogeneous equation associated to (1.2) corresponds to the best discretization of the wave equation (cf. [1, Section 3.14]).
We prove that well posedness, that is, maximal regularity of (1.2) in  vector-valued spaces, is characterized on Banach spaces having the unconditional martingale difference property (
vector-valued spaces, is characterized on Banach spaces having the unconditional martingale difference property ( see, e.g., [4]) by the
see, e.g., [4]) by the  -boundedness of the set
-boundedness of the set

The general framework for the proof of our statement uses a new approach based on operator-valued Fourier multipliers. In the continuous time setting, the relation between operator-valued Fourier multiplier and  boundedness of their symbols is well documented (see, e.g., [5–10]), but we emphasize that the discrete counterpart is too incipient and limited essentially a very few articles (see, e.g., [11, 12]). We believe that the development of this topic could have a strong applied potential. This would lead to very interesting problems related to difference equations arising in numerical analysis, for instance. From this perspective the results obtained in this work are, to the best of our knowledge, new.
boundedness of their symbols is well documented (see, e.g., [5–10]), but we emphasize that the discrete counterpart is too incipient and limited essentially a very few articles (see, e.g., [11, 12]). We believe that the development of this topic could have a strong applied potential. This would lead to very interesting problems related to difference equations arising in numerical analysis, for instance. From this perspective the results obtained in this work are, to the best of our knowledge, new.
We recall that in the continuous case, it is well known that the study of maximal regularity is very useful for treating semilinear and quasilinear problems. (see, e.g., Amann [13], Denk et al. [8], Clément et al. [14], the survey by Arendt [7] and the bibliography therein). However it should be noted that for nonlinear discrete time evolution equations some additional difficulties appear. In fact, we observe that this approach cannot be done by a direct translation of the proofs from the continuous time setting to the discrete time setting. Indeed, the former only allows to construct a solution on a (possibly very short) time interval, the global solution being then obtained by extension results. This technique will obviously fail in the discrete time setting, where no such thing as an arbitrary short time interval exists. In the recent work [15], the authors have found a way around the "short time interval" problem to treat semilinear problems for certain evolution equations of second order. One more case merits mentioning here is Volterra difference equations which describe processes whose current state is determined by their entire prehistory (see, e.g., [16, 17], and the references given there). These processes are encountered, for example, in mathematical models in population dynamics as well as in models of propagation of perturbation in matter with memory. In this direction one of the authors in [18] considered maximal regularity for Volterra difference equations with infinite delay.
The paper is organized as follows. The second section provides the definitions and preliminary results to be used in the theorems stated and proved in this work. In particular to facilitate a comprehensive understanding to the reader we have supplied several basic  -boundedness properties. In the third section, we will give a geometrical link for the best discretization of the harmonic oscillator equation. In the fourth section, we treat the existence and uniqueness problem for (1.2). In the fifth section, we obtain a characterization about maximal regularity for (1.2).
-boundedness properties. In the third section, we will give a geometrical link for the best discretization of the harmonic oscillator equation. In the fourth section, we treat the existence and uniqueness problem for (1.2). In the fifth section, we obtain a characterization about maximal regularity for (1.2).
2. Preliminaries
Let  and
and  be the Banach spaces, let
be the Banach spaces, let  be the space of bounded linear operators from
be the space of bounded linear operators from  into
into  . Let
. Let  denote the set of nonnegative integer numbers,
denote the set of nonnegative integer numbers,  the forward difference operator of the first order, that is, for each
the forward difference operator of the first order, that is, for each  and
and  We introduce the means
We introduce the means

for 
Definition 2.1.
Let  ,
,  be Banach spaces. A subset
be Banach spaces. A subset  of
of  is called
is called  -bounded if there exists a constant
-bounded if there exists a constant  such that
such that

for all  The least
The least  such that (2.2) is satisfied is called the
such that (2.2) is satisfied is called the  -bound of
-bound of  and is denoted
and is denoted 
An equivalent definition using the Rademacher functions can be found in [8]. We note that  -boundedness clearly implies uniformly boundedness. In fact, we have that
-boundedness clearly implies uniformly boundedness. In fact, we have that  If
If  , the notion of
, the notion of  -boundedness is strictly stronger than boundedness unless the underlying space is isomorphic to a Hilbert space [5, Proposition 1.17]. Some useful criteria for
-boundedness is strictly stronger than boundedness unless the underlying space is isomorphic to a Hilbert space [5, Proposition 1.17]. Some useful criteria for  -boundedness are provided in [5, 8, 19]. We remark that the concept of
-boundedness are provided in [5, 8, 19]. We remark that the concept of  -boundedness plays a fundamental role in recent works by Clément and Da Prato [20], Clément et al. [21], Weis [9, 10], Arendt and Bu [5, 6], as well as Keyantuo and Lizama [22–25].
-boundedness plays a fundamental role in recent works by Clément and Da Prato [20], Clément et al. [21], Weis [9, 10], Arendt and Bu [5, 6], as well as Keyantuo and Lizama [22–25].
Remark 2.2.
-
(a)
Let
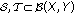 be
be  -bounded sets, then
-bounded sets, then  is
is 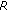 - bounded.
- bounded. -
(b)
Let
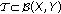 and
and  be
be  -bounded sets, then
-bounded sets, then  is
is 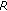 - bounded and
- bounded and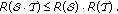 (2.3)
(2.3) -
(c)
Also, each subset
 of the form
of the form  is
is 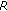 - bounded whenever
- bounded whenever 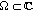 is bounded.
is bounded.
A Banach space  is said to be
is said to be  , if the Hilbert transform is bounded on
, if the Hilbert transform is bounded on  for some (and then all)
for some (and then all)  Here the Hilbert transform
Here the Hilbert transform  of a function
of a function  , the Schwartz space of rapidly decreasing
, the Schwartz space of rapidly decreasing  -valued functions, is defined by
-valued functions, is defined by

These spaces are also called  spaces. It is a well-known theorem that the set of Banach spaces of class
spaces. It is a well-known theorem that the set of Banach spaces of class  coincides with the class of
coincides with the class of  spaces. This has been shown by Bourgain [4] and Burkholder [26]. The following result on operator-valued Fourier multipliers on
spaces. This has been shown by Bourgain [4] and Burkholder [26]. The following result on operator-valued Fourier multipliers on  , due to Blunck [11], is the key for our purposes. Note that for
, due to Blunck [11], is the key for our purposes. Note that for  the Fourier transform on
the Fourier transform on  is defined as
is defined as

Theorem 2.3.
Let  and
and  be a
be a  space. Let
space. Let  and
and  be a differentiable function such that the set
be a differentiable function such that the set

is  -bounded. Then
-bounded. Then  for the following Fourier multiplier
for the following Fourier multiplier  :
:

Recall that  is called analytic if the set
is called analytic if the set

is bounded. For recent and related results on analytic operators we refer to [27].
3. Spectral Properties and Open Problems
In this section we first give a geometrical link between the best discretization (1.2) and the equations of the form

The motivation comes from the recent article of Cieśliński and Ratkiewicz [2], where several discretizations of second-order linear ordinary differential equations with constant coefficients are compared and discussed. More precisely, concerning the harmonic oscillator equation  the following three discrete equations are considered:
the following three discrete equations are considered:

In particular, it is proved in [2] that the best (called "exact" in that paper) discretization of the harmonic oscillator is given by

which reminds the "symmetric" version of Euler's discretization scheme, but  that appears in the discretization of the second derivative is replaced by
that appears in the discretization of the second derivative is replaced by  .
.
Remark 3.1.
Observe that (3.1) can be rewritten as

If  in (3.1), then we have a well-defined recurrence relation of order
in (3.1), then we have a well-defined recurrence relation of order  in case
in case  or
or  (and of order
(and of order  ) in case
) in case  .
.
In case  , we have
, we have  , that is, a recurrence relation of order
, that is, a recurrence relation of order  , which can be not well defined unless
, which can be not well defined unless  . Finally, in case
. Finally, in case  ,
,  is of order
is of order  (note that here we need
(note that here we need  ).
).
Taking (formally) Fourier transform to (3.1), we obtain

Hence the operator  is invertible if and only if
is invertible if and only if  belongs to the resolvent set
belongs to the resolvent set  of
of  . Define the function
. Define the function

Then, for each  fixed,
fixed,  describes a curve in the complex plane such that
describes a curve in the complex plane such that 
Proposition 3.2.
The curve  attains the minimum length at
attains the minimum length at 
Proof.
A calculation gives  Hence the length of
Hence the length of  is given by
is given by

From which the conclusion follows.
Remark 3.3.
As a consequence, the value  in (3.1) is singular in the sense that the curve described by (3.6) attains the minimum length if and only if
in (3.1) is singular in the sense that the curve described by (3.6) attains the minimum length if and only if  (see Figure 1). This singular character is reinforced by observing that
(see Figure 1). This singular character is reinforced by observing that

and that this value exactly corresponds to the step size in the best discretization of the harmonic oscillator obtained in [2]. We conjecture that there is a general link between the geometrical properties of curves related to classes of difference equations and the property of best approximation. This is possibly a very difficult task, which we do not touch in this paper.

Figure 1
In what follows we denote  ;
;  and
and  The following result relates the values of
The following result relates the values of  with the spectrum of the operator
with the spectrum of the operator  . It will be essential in the proof of our characterization of well posedness for (1.2) in
. It will be essential in the proof of our characterization of well posedness for (1.2) in  -vector-valued spaces given in Section 5 (cf. Theorem 5.2).
-vector-valued spaces given in Section 5 (cf. Theorem 5.2).
Proposition 3.4.
Suppose that  is analytic. Then
is analytic. Then  In particular,
In particular,

Proof.
Let  such that
such that  for all
for all  Define
Define  By the spectral mapping theorem, we have
By the spectral mapping theorem, we have

for all  Hence
Hence

Finally, we observe that 
4. Existence and Uniqueness
In this section, we treat the existence and uniqueness problem for the equation

Remark 4.1.
If  is solution of the equation
is solution of the equation

then  . It follows from induction. In fact, suppose that
. It follows from induction. In fact, suppose that  for all
for all  , choosing
, choosing  in (4.2) we get
in (4.2) we get  .
.
Recall that the convolution of two sequences  and
and  is defined by
is defined by

Also we note that the convolution theorem for the discrete Fourier transform holds, that is,  Further properties can be found in [28, Section 5.1]. Our main result in this section, on existence and uniqueness of solution for (4.1), read as follows.
Further properties can be found in [28, Section 5.1]. Our main result in this section, on existence and uniqueness of solution for (4.1), read as follows.
Theorem 4.2.
Let  , then there exists a unique solution of (4.1) which is given by
, then there exists a unique solution of (4.1) which is given by  , where
, where  satisfies the following equation:
satisfies the following equation:

If  is an analytic operator, one has that
is an analytic operator, one has that

where  is a circle, centered at the origin of the
is a circle, centered at the origin of the  -plane that enclosed all poles of
-plane that enclosed all poles of

Hence,

Proof.
Let  , and
, and  defined by
defined by

Then it is not difficult to see that (4.1) is equivalent to

which has the solution

Denote

Then a calculation shows us that there is an operator  with
with  such that
such that

 satisfy the following equation:
satisfy the following equation:

which is equivalent to

We can see that there are two sequences  in
in  such that
such that

Since  , we have
, we have

On the other hand, using (4.12), we have

Hence, applying Fourier transform in (4.17), we obtain

Given  we define
we define

A direct calculation shows that  , for
, for  . Then by (4.18), we get
. Then by (4.18), we get

Hence

On the other hand, since  is solution of (4.9), we have
is solution of (4.9), we have

and hence

Therefore,

Applying Fourier transform in (4.24) and taking into account (4.21), we have

If  is analytic, we get
is analytic, we get

and the proof is finished.
5. Maximal Regularity
In this section, we obtain a spectral characterization about maximal regularity for (1.2). The following definition is motivated in the paper [11] (see also [3]).
Definition 5.1.
Let  . One says that (4.1) has discrete maximal regularity if
. One says that (4.1) has discrete maximal regularity if  defines a bounded operator
defines a bounded operator  .
.
As consequence of the definition, if (1.2) has discrete maximal regularity, then (1.2) has discrete  -maximal regularity in the following sense: for each
-maximal regularity in the following sense: for each  we have
we have  , where
, where  is the solution of the equation
is the solution of the equation  , for all
, for all  . Moreover,
. Moreover,

A similar analysis as above can be carried out when we consider more general initial conditions, but the price to pay for this is that the proof would certainly require additional  -summability condition on
-summability condition on  The following is the main result of this paper.
The following is the main result of this paper.
Theorem 5.2.
Let  be a UMD space and let
be a UMD space and let  analytic. Then the following assertions are equivalent.
analytic. Then the following assertions are equivalent.
-
(i)
Equation (1.2) has discrete maximal regularity.
-
(ii)
 is
is  -bounded.
-bounded.
Proof.
(i) (ii) Define
(ii) Define  by
by

and the corresponding operator  by
by

By hypothesis,  is well defined and bounded on
is well defined and bounded on  . By Proposition 3.4,
. By Proposition 3.4,  whenever
whenever  . Then, by Theorem 4.2 we have
. Then, by Theorem 4.2 we have

We observe that there exists  such that
such that

Explicitly,  is given by
is given by  . We conclude, from [11, Proposition 1.4], that the set in (ii) is
. We conclude, from [11, Proposition 1.4], that the set in (ii) is  -bounded.
-bounded.
(ii) (i) Define
(i) Define  for
for  . Then
. Then  is
is  -bounded by hypothesis and Remark 2.2. Define
-bounded by hypothesis and Remark 2.2. Define

then  and
and  is
is  -bounded. A calculation shows that
-bounded. A calculation shows that  Note that
Note that  is
is  -bounded if and only if
-bounded if and only if  is
is  -bounded (cf. Remark 2.2). Moreover,
-bounded (cf. Remark 2.2). Moreover,

It shows that the set  is
is  -bounded, thanks to Remark 2.6 again. It follows the
-bounded, thanks to Remark 2.6 again. It follows the  -boundedness of the set
-boundedness of the set  . Then, by Theorem 2.7 we obtain that there exists
. Then, by Theorem 2.7 we obtain that there exists  such that
such that

By Theorem 4.2, we have

Then, by uniqueness of the Fourier transform, we conclude that 
Remark 5.3.
Note that

is  -bounded if and only if
-bounded if and only if

is  -bounded.
-bounded.
Corollary 5.4.
Let  be a Hilbert space and let
be a Hilbert space and let  be an analytic operator. Then the following assertions are equivalent.
be an analytic operator. Then the following assertions are equivalent.
-
(i)
Equation (1.2) has discrete maximal regularity.
-
(ii)
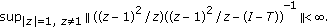
Remark 5.5.
Letting  and
and  with
with  , we get that the hypothesis of the preceding corollary are satisfied. We conclude that the scalar equation
, we get that the hypothesis of the preceding corollary are satisfied. We conclude that the scalar equation

has the property that for all  we get
we get  In particular
In particular  that is, the solution is stable. Note that using (4.7) we can infer that
that is, the solution is stable. Note that using (4.7) we can infer that

where  and
and  are the real roots of
are the real roots of  Moreover, the solution is given by
Moreover, the solution is given by

Remark 5.6.
We emphasize that from a more theoretical perspective, our results also are true when we consider the more general equation (3.1) instead of (1.1), but additional hypothesis will be needed (cf. Remark 3.1). Until now literature about this subject is too incipient and should be developed.
References
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Applications, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Cieśliński JL, Ratkiewicz B: On simulations of the classical harmonic oscillator equation by difference equations. Advances in Difference Equations 2006, 2006:-17.
Cuevas C, Lizama C: Maximal regularity of discrete second order Cauchy problems in Banach spaces. Journal of Difference Equations and Applications 2007,13(12):1129–1138. 10.1080/10236190701458857
Bourgain J: Some remarks on Banach spaces in which martingale difference sequences are unconditional. Arkiv för Matematik 1983,21(2):163–168. 10.1007/BF02384306
Arendt W, Bu S: The operator-valued Marcinkiewicz multiplier theorem and maximal regularity. Mathematische Zeitschrift 2002,240(2):311–343. 10.1007/s002090100384
Arendt W, Bu S: Operator-valued Fourier multipliers on periodic Besov spaces and applications. Proceedings of the Edinburgh Mathematical Society 2004,47(1):15–33. 10.1017/S0013091502000378
Arendt W: Semigroups and evolution equations: functional calculus, regularity and kernel estimates. In Evolutionary Equations, Handbook of Differential Equations. Volume 1. North-Holland, Amsterdam, The Netherlands; 2004:1–85.
Denk R, Hieber M, Prüss J: -boundedness, Fourier multipliers and problems of elliptic and parabolic type. Memoirs of the American Mathematical Society 2003,166(788):1–114.
Weis L: Operator-valued Fourier multiplier theorems and maximal -regularity. Mathematische Annalen 2001,319(4):735–758. 10.1007/PL00004457
Weis L: A new approach to maximal -regularity. In Evolution Equations and Their Applications in Physical and Life Sciences (Bad Herrenalb, 1998), Lecture Notes in Pure and Applied Mathematics. Volume 215. Marcel Dekker, New York, NY, USA; 2001:195–214.
Blunck S: Maximal regularity of discrete and continuous time evolution equations. Studia Mathematica 2001,146(2):157–176. 10.4064/sm146-2-3
Blunck S: Analyticity and discrete maximal regularity on -spaces. Journal of Functional Analysis 2001,183(1):211–230. 10.1006/jfan.2001.3740
Amann H: Quasilinear parabolic functional evolution equations. In Recent Advances on Elliptic and Parabolic Issues: Proceedings of the 2004 Swiss—Japanese Seminar. Edited by: Chipot M, Ninomiya H. World Scientific, Hackensack, NJ, USA; 2006:19–44.
Clément Ph, Londen S-O, Simonett G: Quasilinear evolutionary equations and continuous interpolation spaces. Journal of Differential Equations 2004,196(2):418–447. 10.1016/j.jde.2003.07.014
Cuevas C, Lizama C: Semilinear evolution equations of second order via maximal regularity. Advances in Difference Equations 2008, 2008:-20.
Cardoso F, Cuevas C: Exponential dichotomy and boundedness for retarded functional difference equations. Journal of Difference Equations and Applications 2009,15(3):261–290. 10.1080/10236190802125330
Kolmanovskii VB, Castellanos-Velasco E, Torres-Muñoz JA: A survey: stability and boundedness of Volterra difference equations. Nonlinear Analysis: Theory, Methods & Applications 2003,53(7–8):861–928. 10.1016/S0362-546X(03)00021-X
Cuevas C, Vidal C: A note on discrete maximal regularity for functional difference equations with infinite delay. Advances in Difference Equations 2006, 2006:-11.
Girardi M, Weis L: Operator-valued Fourier multiplier theorems on Besov spaces. Mathematische Nachrichten 2003,251(1):34–51. 10.1002/mana.200310029
Clément Ph, Da Prato G: Existence and regularity results for an integral equation with infinite delay in a Banach space. Integral Equations and Operator Theory 1988,11(4):480–500. 10.1007/BF01199303
Clément Ph, de Pagter B, Sukochev FA, Witvliet H: Schauder decomposition and multiplier theorems. Studia Mathematica 2000,138(2):135–163.
Keyantuo V, Lizama C: Maximal regularity for a class of integro-differential equations with infinite delay in Banach spaces. Studia Mathematica 2005,168(1):25–50. 10.4064/sm168-1-3
Keyantuo V, Lizama C: Fourier multipliers and integro-differential equations in Banach spaces. Journal of the London Mathematical Society 2004,69(3):737–750. 10.1112/S0024610704005198
Keyantuo V, Lizama C: Periodic solutions of second order differential equations in Banach spaces. Mathematische Zeitschrift 2006,253(3):489–514. 10.1007/s00209-005-0919-1
Keyantuo V, Lizama C: Hölder continuous solutions for integro-differential equations and maximal regularity. Journal of Differential Equations 2006,230(2):634–660. 10.1016/j.jde.2006.07.018
Burkholder DL: A geometric condition that implies the existence of certain singular integrals of Banach-space-valued functions. In Conference on Harmonic Analysis in Honor of Antoni Zygmund, Vol. I, II (Chicago, Ill., 1981), Wadsworth Mathematics Series. Edited by: Becker W, Calderón AP, Fefferman R, Jones PW. Wadsworth, Belmont, Calif, USA; 1983:270–286.
Dungey N: A note on time regularity for discrete time heat kernels. Semigroup Forum 2006,72(3):404–410. 10.1007/s00233-005-0549-2
Elaydi S: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 3rd edition. Springer, New York, NY, USA; 2005:xxii+539.
Acknowledgments
The authors are very grateful to the referee for pointing out omissions and providing nice comments and suggestions. This work was done while the third author was visiting the Departamento de Matemática, Universidade Federal de Pernambuco, Recife, Brazil. The second author is partially supported by CNPQ/Brazil. The third author is partially financed by Laboratorio de Análisis Estocástico, Proyecto Anillo ACT-13, and CNPq/Brazil under Grant 300702/2007-08.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Castro, A., Cuevas, C. & Lizama, C. Maximal Regularity of the Discrete Harmonic Oscillator Equation. Adv Differ Equ 2009, 290625 (2009). https://doi.org/10.1155/2009/290625
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/290625
 be
be  -bounded sets, then
-bounded sets, then  is
is  - bounded.
- bounded. and
and  be
be  -bounded sets, then
-bounded sets, then  is
is 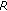 - bounded and
- bounded and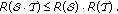
 of the form
of the form  is
is 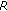 - bounded whenever
- bounded whenever 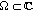 is bounded.
is bounded. is
is  -bounded.
-bounded.