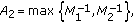- Research Article
- Open access
- Published:
Existence of Positive Solutions for Multipoint Boundary Value Problem with 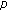 -Laplacian on Time Scales
-Laplacian on Time Scales
Advances in Difference Equations volume 2009, Article number: 312058 (2009)
Abstract
We consider the existence of positive solutions for a class of second-order multi-point boundary value problem with  -Laplacian on time scales. By using the well-known Krasnosel'ski's fixed-point theorem, some new existence criteria for positive solutions of the boundary value problem are presented. As an application, an example is given to illustrate the main results.
-Laplacian on time scales. By using the well-known Krasnosel'ski's fixed-point theorem, some new existence criteria for positive solutions of the boundary value problem are presented. As an application, an example is given to illustrate the main results.
1. Introduction
The theory of time scales has become a new important mathematical branch since it was introduced by Hilger [1]. Theoretically, the time scales approach not only unifies calculus of differential and difference equations, but also solves other problems that are a mix of stop start and continuous behavior. Practically, the time scales calculus has a tremendous potential for application, for example, Thomas believes that time scales calculus is the best way to understand Thomas models populations of mosquitoes that carry West Nile virus [2]. In addition, Spedding have used this theory to model how students suffering from the eating disorder bulimia are influenced by their college friends; with the theory on time scales, they can model how the number of sufferers changes during the continuous college term as well as during long breaks [2]. By using the theory on time scales we can also study insect population, biology, heat transfer, stock market, epidemic models [2–6], and so forth. At the same time, motivated by the wide application of boundary value problems in physical and applied mathematics, boundary value problems for dynamic equations with p-Laplacian on time scales have received lots of interest [7–16].
In [7], Anderson et al. considered the following three-point boundary value problem with p-Laplacian on time scales:

where  , and
, and  for some positive constants
for some positive constants  They established the existence results for at least one positive solution by using a fixed point theorem of cone expansion and compression of functional type.
They established the existence results for at least one positive solution by using a fixed point theorem of cone expansion and compression of functional type.
For the same boundary value problem, He in [8] using a new fixed point theorem due to Avery and Henderson obtained the existence results for at least two positive solutions.
In [9], Sun and Li studied the following one-dimensional p-Laplacian boundary value problem on time scales:

where  is a nonnegative rd-continuous function defined in
is a nonnegative rd-continuous function defined in  and satisfies that there exists
and satisfies that there exists  such that
such that  is a nonnegative continuous function defined on
is a nonnegative continuous function defined on  for some positive constants
for some positive constants  They established the existence results for at least single, twin, or triple positive solutions of the above problem by using Krasnosel'skii's fixed point theorem, new fixed point theorem due to Avery and Henderson and Leggett-Williams fixed point theorem.
They established the existence results for at least single, twin, or triple positive solutions of the above problem by using Krasnosel'skii's fixed point theorem, new fixed point theorem due to Avery and Henderson and Leggett-Williams fixed point theorem.
For the Sturm-Liouville-like boundary value problem, in [17] Ji and Ge investigated a class of Sturm-Liouville-like four-point boundary value problem with p-Laplacian:

where  By using fixed-point theorem for operators on a cone, they obtained some existence of at least three positive solutions for the above problem. However, to the best of our knowledge, there has not any results concerning the similar problems on time scales.
By using fixed-point theorem for operators on a cone, they obtained some existence of at least three positive solutions for the above problem. However, to the best of our knowledge, there has not any results concerning the similar problems on time scales.
Motivated by the above works, in this paper we consider the following multi-point boundary value problem on time scales:

where  and we denote
and we denote  with
with 
In the following, we denote  for convenience. And we list the following hypotheses:
for convenience. And we list the following hypotheses:
-
(C1)
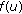 is a nonnegative continuous function defined on
is a nonnegative continuous function defined on 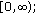
-
(C2)
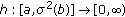 is rd-continuous with
is rd-continuous with 
2. Preliminaries
In this section, we provide some background material to facilitate analysis of problem (1.4).
Let the Banach space  is rd-continuous
is rd-continuous be endowed with the norm
be endowed with the norm  and choose the cone
and choose the cone  defined by
defined by

It is easy to see that the solution of BVP (1.4) can be expressed as

If  where
where

we define the operator  by
by

It is easy to see  ,
,  for
for  and if
and if  then
then  is the positive solution of BVP (1.4).
is the positive solution of BVP (1.4).
From the definition of  for each
for each  we have
we have  and
and 
In fact,

is continuous and nonincreasing in  Moreover,
Moreover,  is a monotone increasing continuously differentiable function,
is a monotone increasing continuously differentiable function,

then by the chain rule on time scales, we obtain

so, 
For the notational convenience, we denote

Lemma 2.1.
 is completely continuous.
is completely continuous.
Proof.
First, we show that  maps bounded set into bounded set.
maps bounded set into bounded set.
Assume that  is a constant and
is a constant and  Note that the continuity of
Note that the continuity of  guarantees that there exists
guarantees that there exists  such that
such that  . So
. So

That is,  is uniformly bounded. In addition, it is easy to see
is uniformly bounded. In addition, it is easy to see

So, by applying Arzela-Ascoli Theorem on time scales, we obtain that  is relatively compact.
is relatively compact.
Second, we will show that  is continuous. Suppose that
is continuous. Suppose that  and
and  converges to
converges to  uniformly on
uniformly on  . Hence,
. Hence,  is uniformly bounded and equicontinuous on
is uniformly bounded and equicontinuous on  . The Arzela-Ascoli Theorem on time scales tells us that there exists uniformly convergent subsequence in
. The Arzela-Ascoli Theorem on time scales tells us that there exists uniformly convergent subsequence in  . Let
. Let  be a subsequence which converges to
be a subsequence which converges to  uniformly on
uniformly on  . In addition,
. In addition,

Observe that

Inserting  into the above and then letting
into the above and then letting  , we obtain
, we obtain

here we have used the Lebesgues dominated convergence theorem on time scales. From the definition of  , we know that
, we know that  on
on  . This shows that each subsequence of
. This shows that each subsequence of  uniformly converges to
uniformly converges to  . Therefore, the sequence
. Therefore, the sequence  uniformly converges to
uniformly converges to  . This means that
. This means that  is continuous at
is continuous at  . So,
. So,  is continuous on
is continuous on  since
since  is arbitrary. Thus,
is arbitrary. Thus,  is completely continuous.
is completely continuous.
The proof is complete.
Lemma 2.2.
Let  then
then  for
for  and
and  for
for 
Proof.
Since  , it follows that
, it follows that  is nonincreasing. Hence, for
is nonincreasing. Hence, for  ,
,

from which we have

For 

we know

The proof is complete.
Lemma 2.3 ([18]).
Let  be a cone in a Banach space
be a cone in a Banach space  Assum that
Assum that  are open subsets of
are open subsets of  with
with  If
If

is a completely continuous operator such that either
-
(i)
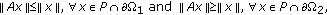 or
or -
(ii)

Then  has a fixed point in
has a fixed point in 
3. Main Results
In this section, we present our main results with respect to BVP (1.4).
For the sake of convenience, we define  number of zeros in the set
number of zeros in the set  , and
, and  number of
number of  in the set
in the set 
Clearly,  or 2 and there are six possible cases:
or 2 and there are six possible cases:
-
(i)

-
(ii)
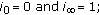
-
(iii)
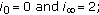
-
(iv)

-
(v)
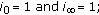
-
(vi)

Theorem 3.1.
BVP (1.4) has at least one positive solution in the case  and
and 
Proof.
First, we consider the case  and
and  Since
Since  then there exists
then there exists  such that
such that  for
for  where
where  satisfies
satisfies

If  with
with  then
then

It follows that if  then
then  for
for 
Since  then there exists
then there exists  such that
such that  for
for  where
where  is chosen such that
is chosen such that

Set  and
and 
If  with
with  then
then

So that

In other words, if  then
then  Thus by
Thus by  of Lemma 2.3, it follows that
of Lemma 2.3, it follows that  has a fixed point in
has a fixed point in  with
with  .
.
Now we consider the case  and
and  Since
Since  there exists
there exists  such that
such that  for
for  , where
, where  is such that
is such that

If  with
with  then we have
then we have

Thus, we let  so that
so that  for
for 
Next consider  By definition, there exists
By definition, there exists  such that
such that  for
for  , where
, where  satisfies
satisfies

Suppose  is bounded, then
is bounded, then  for all
for all  pick
pick

If  with
with  then
then

Now suppose  is unbounded. From condition
is unbounded. From condition  it is easy to know that there exists
it is easy to know that there exists  such that
such that  for
for  If
If  with
with  then by using (3.8) we have
then by using (3.8) we have

Consequently, in either case we take

so that for  we have
we have  Thus by (ii) of Lemma 2.3, it follows that
Thus by (ii) of Lemma 2.3, it follows that  has a fixed point
has a fixed point  in
in  with
with 
The proof is complete.
Theorem 3.2.
Suppose  , and the following conditions hold,
, and the following conditions hold,
-
(C3):
there exists constant
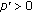 such that
such that  for
for  where
where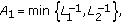 (3.13)
(3.13) -
(C4):
there exists constant
 such that
such that 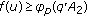 for
for  where
where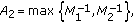 (3.14)
(3.14)
furthermore,  Then BVP (1.4) has at least one positive solution
Then BVP (1.4) has at least one positive solution  such that
such that  lies between
lies between  and
and 
Proof.
Without loss of generality, we may assume that 
Let  for any
for any  In view of
In view of  we have
we have

which yields

Now set  for
for  we have
we have

Hence by condition  we can get
we can get

So if we take  then
then

Consequently, in view of  (3.16), and (3.19), it follows from Lemma 2.3 that
(3.16), and (3.19), it follows from Lemma 2.3 that  has a fixed point
has a fixed point  in
in  Moreover, it is a positive solution of (1.4) and
Moreover, it is a positive solution of (1.4) and 
The proof is complete.
For the case  or
or  we have the following results.
we have the following results.
Theorem 3.3.
Suppose that  and
and  hold. Then BVP (1.4) has at least one positive solution.
hold. Then BVP (1.4) has at least one positive solution.
Proof.
It is easy to see that under the assumptions, the conditions  and
and  in Theorem 3.2 are satisfied. So the proof is easy and we omit it here.
in Theorem 3.2 are satisfied. So the proof is easy and we omit it here.
Theorem 3.4.
Suppose that  and
and  hold. Then BVP (1.4) has at least one positive solution.
hold. Then BVP (1.4) has at least one positive solution.
Proof.
Since  for
for  there exists a sufficiently small
there exists a sufficiently small  such that
such that

Thus, if  , then we have
, then we have

by the similar method, one can get if  then
then

So, if we choose  then for
then for  we have
we have  which yields condition
which yields condition  in Theorem 3.2.
in Theorem 3.2.
Next, by  for
for  there exists a sufficiently large
there exists a sufficiently large  such that
such that

where we consider two cases.
Case 1.
Suppose that  is bounded, say
is bounded, say

In this case, take sufficiently large  such that
such that  then from (3.24), we know
then from (3.24), we know  for
for  which yields condition
which yields condition  in Theorem 3.2.
in Theorem 3.2.
Case 2.
Suppose that  is unbounded. it is easy to know that there is
is unbounded. it is easy to know that there is  such that
such that

Since  then from (3.23) and (3.25), we get
then from (3.23) and (3.25), we get

Thus, the condition  of Theorem 3.2 is satisfied.
of Theorem 3.2 is satisfied.
Hence, from Theorem 3.2, BVP (1.4) has at least one positive solution.
The proof is complete.
From Theorems 3.3 and 3.4, we have the following two results.
Corollary 3.5.
Suppose that  and the condition
and the condition  in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
Corollary 3.6.
Suppose that  and the condition
and the condition  in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
Theorem 3.7.
Suppose that  and
and  hold. Then BVP (1.4) has at least one positive solution.
hold. Then BVP (1.4) has at least one positive solution.
Proof.
In view of  similar to the first part of Theorem 3.1, we have
similar to the first part of Theorem 3.1, we have

Since  for
for  there exists a sufficiently small
there exists a sufficiently small  such that
such that

Similar to the proof of Theorem 3.2, we obtain

The result is obtained, and the proof is complete.
Theorem 3.8.
Suppose that  and
and  hold. Then BVP (1.4) has at least one positive solution.
hold. Then BVP (1.4) has at least one positive solution.
Proof.
Since  similar to the second part of Theorem 3.1, we have
similar to the second part of Theorem 3.1, we have  for
for 
By  similar to the second part of proof of Theorem 3.4, we have
similar to the second part of proof of Theorem 3.4, we have  where
where  Thus BVP (1.4) has at least one positive solution.
Thus BVP (1.4) has at least one positive solution.
The proof is complete.
From Theorems 3.7 and 3.8, we can get the following corollaries.
Corollary 3.9.
Suppose that  and the condition
and the condition  in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
Corollary 3.10.
Suppose that  and the condition
and the condition  in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
in Theorem 3.2 hold. Then BVP (1.4) has at least one positive solution.
Theorem 3.11.
Suppose that  and the condition
and the condition  of Theorem 3.2 hold. Then BVP (1.4) has at least two positive solutions
of Theorem 3.2 hold. Then BVP (1.4) has at least two positive solutions  such that
such that 
Proof.
By using the method of proving Theorems 3.1 and 3.2, we can deduce the conclusion easily, so we omit it here.
Theorem 3.12.
Suppose that  and the condition
and the condition  of Theorem 3.2 hold. Then BVP (1.4) has at least two positive solutions
of Theorem 3.2 hold. Then BVP (1.4) has at least two positive solutions  such that
such that 
Proof.
Combining the proofs of Theorems 3.1 and 3.2, the conclusion is easy to see, and we omit it here.
4. Applications and Examples
In this section, we present a simple example to explain our result. When  ,
,

where, 
It is easy to see that the condition  and
and  are satisfied and
are satisfied and

So, by Theorem 3.1, the BVP (4.1) has at least one positive solution.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1–2):18–56.
Spedding V: Taming nature's numbers. New Scientist 2003, 28–32.
Jones MA, Song B, Thomas DM: Controlling wound healing through debridement. Mathematical and Computer Modelling 2004,40(9–10):1057–1064. 10.1016/j.mcm.2003.09.041
Thomas DM, Vandemuelebroeke L, Yamaguchi K: A mathematical evolution model for phytoremediation of metals. Discrete and Continuous Dynamical Systems. Series B 2005,5(2):411–422.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Anderson D, Avery R, Henderson J: Existence of solutions for a one dimensional -Laplacian on time-scales. Journal of Difference Equations and Applications 2004,10(10):889–896. 10.1080/10236190410001731416
He Z: Double positive solutions of three-point boundary value problems for -Laplacian dynamic equations on time scales. Journal of Computational and Applied Mathematics 2005,182(2):304–315. 10.1016/j.cam.2004.12.012
Sun H-R, Li W-T: Existence theory for positive solutions to one-dimensional -Laplacian boundary value problems on time scales. Journal of Differential Equations 2007,240(2):217–248. 10.1016/j.jde.2007.06.004
Li W-T, Sun HR: Positive solutions for second-order -point boundary value problems on time scales. Acta Mathematica Sinica 2006,22(6):1797–1804. 10.1007/s10114-005-0748-5
Sun HR: Boundary value problems for dynamic equations on measure chains, Ph. D. thesis. Lanzhou University, Lanzhou, China; 2004.
Anderson DR: Existence of solutions for a first-order -Laplacian BVP on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4521–4525. 10.1016/j.na.2007.11.008
Su Y-H, Li W-T, Sun H-R: Positive solutions of singular -Laplacian BVPs with sign changing nonlinearity on time scales. Mathematical and Computer Modelling 2008,48(5–6):845–858. 10.1016/j.mcm.2007.11.008
Zhang X, Ge W: Existence of positive solutions for a class of -point boundary value problems. Advances in Difference Equations 2008, 2008:-9.
Feng M, Li X, Ge W: Triple positive solutions of fourth-order four-point boundary value problems for -Laplacian dynamic equations on time scales. Advances in Difference Equations 2008, 2008:-9.
Song C: Eigenvalue problems for -Laplacian functional dynamic equations on time scales. Advances in Difference Equations 2008, 2008:-9.
Ji D, Ge W: Existence of multiple positive solutions for Sturm-Liouville-like four-point boundary value problem with -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008,68(9):2638–2646. 10.1016/j.na.2007.02.010
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, San Diego, Calif, USA; 1988:viii+275.
Acknowledgments
This research is supported by the Natural Science Foundation of China (60774004), China Postdoctoral Science Foundation Funded Project (20080441126), Shandong Postdoctoral Funded Project (200802018), the Natural Science Foundation of Shandong (Y2007A27, Y2008A28), and the Fund of Doctoral Program Research of University of Jinan (B0621, XBS0843).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, M., Sun, S. & Han, Z. Existence of Positive Solutions for Multipoint Boundary Value Problem with 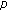 -Laplacian on Time Scales.
Adv Differ Equ 2009, 312058 (2009). https://doi.org/10.1155/2009/312058
-Laplacian on Time Scales.
Adv Differ Equ 2009, 312058 (2009). https://doi.org/10.1155/2009/312058
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/312058
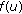 is a nonnegative continuous function defined on
is a nonnegative continuous function defined on 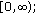
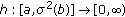 is rd-continuous with
is rd-continuous with 
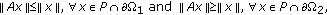 or
or

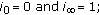
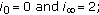

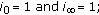

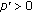 such that
such that  for
for  where
where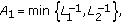
 such that
such that 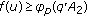 for
for  where
where