- Research Article
- Open access
- Published:
Inequalities among Eigenvalues of Second-Order Difference Equations with General Coupled Boundary Conditions
Advances in Difference Equations volume 2009, Article number: 347291 (2009)
Abstract
This paper studies general coupled boundary value problems for second-order difference equations. Existence of eigenvalues is proved, numbers of their eigenvalues are calculated, and their relationships between the eigenvalues of second-order difference equation with three different coupled boundary conditions are established.
1. Introduction
Consider the second-order difference equation

with the general coupled boundary condition

where  is an integer,
is an integer,  is the forward difference operator:
is the forward difference operator:  ,
,  is the backward difference operator:
is the backward difference operator:  , and
, and  and
and  are real numbers with
are real numbers with  for
for  ,
,  for
for  , and
, and  is the spectral parameter; the interval
is the spectral parameter; the interval  is the integral set
is the integral set  ;
;  ,
,  is a constant parameter;
is a constant parameter;  ,
,

The boundary condition (1.2) contains the periodic and antiperiodic boundary conditions. In fact, (1.2) is the periodic boundary condition in the case where  and
and  , the identity matrix, and (1.2) is the antiperiodic condition in the case where
, the identity matrix, and (1.2) is the antiperiodic condition in the case where  and
and  .
.
We first briefly recall some relative existing results of eigenvalue problems for difference equations. Atkinson [1, Chapter  , Section
, Section  ] discussed the boundary conditions
] discussed the boundary conditions

when he investigated the recurrence formula

where  ,
,  ,
,  ,
,  and
and  are real numbers, subject to
are real numbers, subject to  and
and

He remarked that all the eigenvalues of the boundary value problem (1.4) and (1.5) are real, and they may not be all distinct. If  and
and  , he viewed the boundary conditions (1.4) as the periodic boundary conditions for (1.5). Shi and Chen [2] investigated the more general boundary value problem
, he viewed the boundary conditions (1.4) as the periodic boundary conditions for (1.5). Shi and Chen [2] investigated the more general boundary value problem


where  ,
,  , and
, and  are
are  Hermitian matrices;
Hermitian matrices;  and
and  are nonsingular;
are nonsingular;  for
for  ;
;  and
and  are
are  matrices. Moreover,
matrices. Moreover,  and
and  satisfy rank
satisfy rank and the self-adjoint condition
and the self-adjoint condition  [2, Lemma
[2, Lemma  ]. A series of spectral results was obtained. We will remark that the boundary condition (1.8) includes the coupled boundary condition (1.2) when
]. A series of spectral results was obtained. We will remark that the boundary condition (1.8) includes the coupled boundary condition (1.2) when  , and the boundary conditions (1.4) when (1.6) holds. Agarwal and Wong studied existence of minimal and maximal quasisolutions of a second-order nonlinear periodic boundary value problem [3, Section
, and the boundary conditions (1.4) when (1.6) holds. Agarwal and Wong studied existence of minimal and maximal quasisolutions of a second-order nonlinear periodic boundary value problem [3, Section  ]. In 2005, Wang and Shi [4] considered (1.1) with the periodic and antiperiodic boundary conditions. They found out the following results (see [4, Theorems
]. In 2005, Wang and Shi [4] considered (1.1) with the periodic and antiperiodic boundary conditions. They found out the following results (see [4, Theorems  and
and  ]): the periodic and antiperiodic boundary value problems have exactly
]): the periodic and antiperiodic boundary value problems have exactly  real eigenvalues
real eigenvalues  and
and  , respectively, which satisfy
, respectively, which satisfy

These results are similar to those about eigenvalues of periodic and antiperiodic boundary value problems for second-order ordinary differential equations (cf. [5–8]).
Motivated by [4], we compare the eigenvalues of the eigenvalue problem (1.1) with the coupled boundary condition (1.2) as  varies and obtain relationships between the eigenvalues in the present paper. These results extend the above results obtained in [4]. In this paper, we will apply some results obtained by Shi and Chen [2] to prove the existence of eigenvalues of (1.1) and (1.2) to calculate the number of these eigenvalues, and to apply some oscillation results obtained by Agarwal et al. [9] to compare the eigenvalues as
varies and obtain relationships between the eigenvalues in the present paper. These results extend the above results obtained in [4]. In this paper, we will apply some results obtained by Shi and Chen [2] to prove the existence of eigenvalues of (1.1) and (1.2) to calculate the number of these eigenvalues, and to apply some oscillation results obtained by Agarwal et al. [9] to compare the eigenvalues as  varies.
varies.
This paper is organized as follows. Section 2 gives some preliminaries including existence and numbers of eigenvalues of the coupled boundary value problems, and some properties of eigenvalues of a kind of separated boundary value problem, which will be used in the next section. Section 3 pays attention to comparison between the eigenvalues of problem (1.1) and (1.2) as  varies.
varies.
2. Preliminaries
Equation (1.1) can be rewritten as the recurrence formula

Clearly,  is a polynomial in
is a polynomial in  with real coefficients since
with real coefficients since  and
and  are all real. Hence, all the solutions of (1.1) are entire functions of
are all real. Hence, all the solutions of (1.1) are entire functions of  . Especially, if
. Especially, if  ,
,  is a polynomial of degree
is a polynomial of degree  in
in  for
for  . However, if
. However, if  and
and  ,
,  is a polynomial of degree
is a polynomial of degree  in
in  for
for  .
.
We now prepare some results that are useful in the next section. The following lemma is mentioned in [4, Theorem  ].
].
Lemma 2.1 ([4, Theorem  ]).
]).
Let  and
and  be any solutions of (1.1). Then the Wronskian
be any solutions of (1.1). Then the Wronskian

is a constant on  .
.
Theorem 2.2.
If  then the coupled boundary value problem (1.1) and (1.2) has exactly
then the coupled boundary value problem (1.1) and (1.2) has exactly  real eigenvalues.
real eigenvalues.
Proof.
By setting  ,
,  ,
,  ,
,

shifting the whole interval  left by one unit, and using
left by one unit, and using  , (1.1) and (1.2) are written as (1.7) and (1.8), respectively. It is evident that
, (1.1) and (1.2) are written as (1.7) and (1.8), respectively. It is evident that  and
and  . Hence, the boundary condition (1.2) is self-adjoint by [2, Lemma
. Hence, the boundary condition (1.2) is self-adjoint by [2, Lemma  ]. In addition, it follows from (2.3) and
]. In addition, it follows from (2.3) and  that
that

By noting that  , we get
, we get  . Therefore, by [2, Theorem
. Therefore, by [2, Theorem  ], the problem (1.1) and (1.2) has exactly
], the problem (1.1) and (1.2) has exactly  real eigenvalues. This completes the proof.
real eigenvalues. This completes the proof.
Let  be the solution of (1.1) with the initial conditions
be the solution of (1.1) with the initial conditions

Consider the sequence

If  for some
for some  , then, we get from (2.1) that
, then, we get from (2.1) that  and
and  have opposite signs. Hence, we say that sequence (2.6) exhibits a change of sign if
have opposite signs. Hence, we say that sequence (2.6) exhibits a change of sign if  for some
for some  , or
, or  for some
for some  . A general zero of the sequence (2.6) is defined as its zero or a change of sign.
. A general zero of the sequence (2.6) is defined as its zero or a change of sign.
Now we consider (1.1) with the following separated boundary conditions:

where  are entries of
are entries of  . It follows from (2.1) that the separated boundary value problem (1.1) with (2.7) has a unique solution, and the separated boundary value problem will be used to compare the eigenvalues of (1.1) and (1.2) as
. It follows from (2.1) that the separated boundary value problem (1.1) with (2.7) has a unique solution, and the separated boundary value problem will be used to compare the eigenvalues of (1.1) and (1.2) as  varies in the next section.
varies in the next section.
In [9], Agarwal et al. studied the following boundary value problem on time scales:

with the boundary conditions

where  is a time scale,
is a time scale,  and
and  are the forward and backward jump operators in
are the forward and backward jump operators in  ,
,  is the delta derivative, and
is the delta derivative, and  ;
;  is continuous;
is continuous;  ;
;  with
with  . They obtained some useful oscillation results. With a similar argument to that used in the proof of [9, Theorem
. They obtained some useful oscillation results. With a similar argument to that used in the proof of [9, Theorem  ], one can show the following result.
], one can show the following result.
Lemma 2.3.
The eigenvalues of the boundary value problem are

with

where  and
and  are real and continuous functions in
are real and continuous functions in  over
over  over
over 
 are arranged as
are arranged as  and an eigenfunction corresponding to
and an eigenfunction corresponding to  has exactly
has exactly  generalized zeros in the open interval
generalized zeros in the open interval  .
.
By setting  ,
,  , the above boundary value problem can be written as (1.1) with (2.7), then we have the following result.
, the above boundary value problem can be written as (1.1) with (2.7), then we have the following result.
Lemma 2.4.
The boundary value problem (1.1) and (2.7) has  real and simple eigenvalues as
real and simple eigenvalues as  and
and  real and simple eigenvalues as
real and simple eigenvalues as  , which can be arranged in the increasing order
, which can be arranged in the increasing order

Let  be the solution of (1.1) with the separated boundary conditions (2.7). Then sequence (2.6) exhibits no changes of sign for
be the solution of (1.1) with the separated boundary conditions (2.7). Then sequence (2.6) exhibits no changes of sign for  , exactly
, exactly  changes of sign for
changes of sign for  , and
, and  changes of sign for
changes of sign for  .
.
Let  and
and  be the solutions of (1.1) satisfying the following initial conditions:
be the solutions of (1.1) satisfying the following initial conditions:

respectively. By Lemma 2.1 and using  , we have
, we have

Obviously,  and
and  are two linearly independent solutions of (1.1). The following lemma can be derived from [4, Proposition
are two linearly independent solutions of (1.1). The following lemma can be derived from [4, Proposition  ].
].
Lemma 2.5.
Let  be the eigenvalues of (1.1) and (2.7) with
be the eigenvalues of (1.1) and (2.7) with  and be arranged as (2.12). Then,
and be arranged as (2.12). Then,  is an eigenfunction of the problem (1.1) and (2.7) with respect to
is an eigenfunction of the problem (1.1) and (2.7) with respect to  , that is, for
, that is, for  ,
,  is a nontrivial solution of (1.1) satisfying
is a nontrivial solution of (1.1) satisfying

Moreover, if  is odd,
is odd,  and if
and if  is even,
is even,  for
for  .
.
A representation of solutions for a nonhomogeneous linear equation with initial conditions is given by the following lemma.
Lemma 2.6 (see [4, Theorem  ]).
]).
For any  and for any
and for any  , the initial value problem
, the initial value problem

has a unique solution  , which can be expressed as
, which can be expressed as

where  .
.
3. Main Results
Let  and
and  be defined in Section 2, let
be defined in Section 2, let  be the eigenvalues of the separated boundary value problem (1.1) with (2.7), and let
be the eigenvalues of the separated boundary value problem (1.1) with (2.7), and let  be the eigenvalues of the coupled boundary value problem (1.1) and (1.2) and arranged in the nondecreasing order
be the eigenvalues of the coupled boundary value problem (1.1) and (1.2) and arranged in the nondecreasing order

Clearly,  denotes the eigenvalue of the problem (1.1) and (1.2) with
denotes the eigenvalue of the problem (1.1) and (1.2) with  , and
, and  denotes the eigenvalue of the problem (1.1) and (1.2) with
denotes the eigenvalue of the problem (1.1) and (1.2) with  . We now present the main results of this paper.
. We now present the main results of this paper.
Theorem 3.1.
Assume that  or
or  . Then, for every fixed
. Then, for every fixed  ,
,  , one has the following inequalities:
, one has the following inequalities:

Remark 3.2.
If  or
or  , a similar result can be obtained by applying Theorem 3.1 to
, a similar result can be obtained by applying Theorem 3.1 to  . In fact,
. In fact,  for
for  and
and  for
for  . Hence, the boundary condition (1.2) in the cases of
. Hence, the boundary condition (1.2) in the cases of  or
or  and
and  , can be written as condition (1.2), where
, can be written as condition (1.2), where  is replaced by
is replaced by  for
for  and
and  for
for  , and
, and  is replaced by
is replaced by  .
.
Before proving Theorem 3.1, we prove the following five propositions.
Proposition 3.3.
For  ,
,  is an eigenvalue of (1.1) and (1.2) if and only if
is an eigenvalue of (1.1) and (1.2) if and only if

where

Moreover,  is a multiple eigenvalue of (1.1) and (1.2) if and only if
is a multiple eigenvalue of (1.1) and (1.2) if and only if

Proof.
Since  and
and  are linearly independent solutions of (1.1), then
are linearly independent solutions of (1.1), then  is an eigenvalue of the problem (1.1) and (1.2) if and only if there exist two constants
is an eigenvalue of the problem (1.1) and (1.2) if and only if there exist two constants  and
and  not both zero such that
not both zero such that  satisfies (1.2), which yields
satisfies (1.2), which yields

It is evident that (3.6) has a nontrivial solution  if and only if
if and only if

which, together with (2.14) and  , implies that
, implies that

Then (3.3) follows from the above relation and the fact that  . On the other hand, (1.1) has two linearly independent solutions satisfying (1.2) if and only if all the entries of the coefficient matrix of (3.6) are zero. Hence,
. On the other hand, (1.1) has two linearly independent solutions satisfying (1.2) if and only if all the entries of the coefficient matrix of (3.6) are zero. Hence,  is a multiple eigenvalue of (1.1) and (1.2) if and only if (3.5) holds. This completes the proof.
is a multiple eigenvalue of (1.1) and (1.2) if and only if (3.5) holds. This completes the proof.
The following result is a direct consequence of the first result of Proposition 3.3.
Corollary 3.4.
For any  ,
,

Proposition 3.5.
Assume that  or
or  . Then one has the following results.
. Then one has the following results.
-
(i)
For each
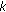 ,
,  ,
, 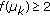 if
if  is odd, and
is odd, and 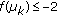 if
if  is even.
is even. -
(ii)
There exists a constant
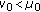 such that
such that  .
. -
(iii)
If the boundary value problem (1.1) and (2.7) has exactly
 eigenvalues then there exists a constant
eigenvalues then there exists a constant 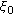 such that
such that  and
and  , where
, where 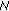 is odd, and there exists a constant
is odd, and there exists a constant  such that
such that 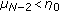 and
and 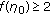 , where
, where 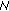 is even.
is even.
Proof.
(i) If  is an eigenfunction of the problem (1.1) and (2.7) respect to
is an eigenfunction of the problem (1.1) and (2.7) respect to  then
then  . By Lemma 2.3 and the initial conditions (2.13), we have that if
. By Lemma 2.3 and the initial conditions (2.13), we have that if  then the sequence
then the sequence  ,
,  exhibits
exhibits  changes of sign and
changes of sign and

Case 1.
If  then it follows from
then it follows from  that
that

By (2.14) and the first relation in (3.11), for each  ,
,  , we have
, we have

By the definition of  , (3.11), and
, (3.11), and 

Hence,

Noting  ,
,  , and (3.10), we have that if
, and (3.10), we have that if  is odd then
is odd then

and if  is even then
is even then

Case 2.
If  then it follows from (2.7) and (2.14) that for each
then it follows from (2.7) and (2.14) that for each  ,
,  ,
,

From (2.15) and by the definition of  , we get
, we get

Hence, noting  ,
,  , and by Lemma 2.5, we have that if
, and by Lemma 2.5, we have that if  is odd, then
is odd, then

and if  is even, then
is even, then

(ii) By the discussions in the first paragraph of Section 2,  is a polynomial of degree
is a polynomial of degree  in
in  ,
,  is a polynomial of degree
is a polynomial of degree  in
in  ,
,  is a polynomial of degree
is a polynomial of degree  in
in  , and
, and  is a polynomial of degree
is a polynomial of degree  in
in  . Further,
. Further,  can be written as
can be written as

where  and
and  is a certain constant for
is a certain constant for  . Then
. Then

where  is a polynomial in
is a polynomial in  whose degree is not larger than
whose degree is not larger than  . Clearly, as
. Clearly, as  ,
,  since
since  . By the first part of this proposition,
. By the first part of this proposition,  . So there exists a constant
. So there exists a constant  such that
such that  .
.
-
(iii)
It follows from the first part of this proposition that if
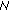 is odd,
is odd,  and if
and if 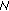 is even,
is even, 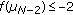 . By (3.22), if
. By (3.22), if  is odd,
is odd, 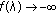 as
as 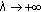 ; if
; if 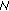 is even,
is even, 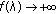 as
as 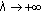 . Hence, if
. Hence, if  is odd, there exists a constant
is odd, there exists a constant  such that
such that  ; if
; if  is even, there exists a constant
is even, there exists a constant 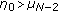 such that
such that  . This completes the proof.
. This completes the proof.
Since  and
and  are both polynomials in
are both polynomials in  , so is
, so is  . Denote
. Denote

Proposition 3.6.
Assume that  or
or  . Equations
. Equations  and
and  or
or  hold if and only if
hold if and only if  is a multiple eigenvalue of (1.1) and (1.2) with
is a multiple eigenvalue of (1.1) and (1.2) with  or
or  . If
. If  or
or  for some
for some  , then
, then  is a simple eigenvalue of (1.1) and (1.2) with
is a simple eigenvalue of (1.1) and (1.2) with  or
or  and for every
and for every  , with
, with  one has:
one has:

Proof.
Since  and
and  are solutions of (1.1), we have
are solutions of (1.1), we have


Differentiating (3.25) and (3.26) with respect to  , respectively, yields that
, respectively, yields that

It follows from (2.13) that

Thus, by Lemma 2.6 and from (3.27)–(3.28), we have

It follows from (3.29) that

Hence, not indicating  explicitly, we get
explicitly, we get

where

which is symmetric for any  . Then, we have
. Then, we have

Hence, if  or
or  , we get from (3.33) that
, we get from (3.33) that  . Then, for any fixed
. Then, for any fixed  with
with  or
or  , the matrix
, the matrix  is positive semidefinite or negative semidefinite. Therefore, for such a
is positive semidefinite or negative semidefinite. Therefore, for such a  ,
,  cannot vanish unless
cannot vanish unless  for all
for all  . Because
. Because  and
and  are linearly independent,
are linearly independent,  is identically zero if and only if all the entries of the matrix
is identically zero if and only if all the entries of the matrix  vanish, namely,
vanish, namely,

which, together with  and
and  , implies
, implies

Then by Proposition 3.3,  is a multiple eigenvalue of (1.1) and (1.2) with
is a multiple eigenvalue of (1.1) and (1.2) with  . In addition, (3.34), together with
. In addition, (3.34), together with  and
and  , implies
, implies

Then by Proposition 3.3,  is a multiple eigenvalue of (1.1) and (1.2) with
is a multiple eigenvalue of (1.1) and (1.2) with  . Conversely, from (3.35) or (3.36), it can be easily verified that (3.34) holds, then
. Conversely, from (3.35) or (3.36), it can be easily verified that (3.34) holds, then  . It follows again from (3.35) or (3.36) that
. It follows again from (3.35) or (3.36) that  or
or  . Thus
. Thus  and
and  or
or  if and only if
if and only if  is a multiple eigenvalue of (1.1) and (1.2) with
is a multiple eigenvalue of (1.1) and (1.2) with  or
or  .
.
Further, for every fixed  with
with  or
or  , not indicating
, not indicating  explicitly, (3.33) implies that
explicitly, (3.33) implies that

Therefore, from (3.37) and by the definition of  , we have
, we have

and consequently, not indicating  explicitly, we have
explicitly, we have

for every fixed  with
with  or
or  .
.
Suppose that  or
or  for some
for some  (
( ), we have
), we have  From the above discussions again,
From the above discussions again,  is a simple eigenvalue of (1.1) and (1.2) with
is a simple eigenvalue of (1.1) and (1.2) with  or
or  , and
, and  is not identically zero for
is not identically zero for  .
.
For this  (
( ), (3.39) implies that
), (3.39) implies that  , and from Proposition 3.5 (i), (ii) that
, and from Proposition 3.5 (i), (ii) that  ,
,  . Hence,
. Hence,  , where
, where  . It follows from Proposition 3.5 (i) that
. It follows from Proposition 3.5 (i) that  and
and  , where
, where  . By Proposition 3.5 (i), (iii),
. By Proposition 3.5 (i), (iii),  and there exists
and there exists  such that
such that  if
if  is odd, and
is odd, and  and there exists
and there exists  such that
such that  if
if  is even. Hence,
is even. Hence,  where
where  . This completes the proof.
. This completes the proof.
Proposition 3.7.
For any fixed  ,
,  , each eigenvalue of (1.1) and (1.2) is simple.
, each eigenvalue of (1.1) and (1.2) is simple.
Proof.
Fix  ,
,  with
with  . Suppose that
. Suppose that  is an eigenvalue of the problem (1.1) and (1.2). By Proposition 3.3, we have
is an eigenvalue of the problem (1.1) and (1.2). By Proposition 3.3, we have  . It follows from (3.33) that
. It follows from (3.33) that  and the matrix
and the matrix  is positive definite or negative definite. Hence,
is positive definite or negative definite. Hence,  for
for  or
or  for
for  since
since  and
and  are linearly independent.
are linearly independent.
If  is a multiple eigenvalue of problem (1.1) and (1.2), then (3.5) holds by Proposition 3.3. By using (3.5), it can be easily verified that (3.34) holds, that is, all the entries of the matrix
is a multiple eigenvalue of problem (1.1) and (1.2), then (3.5) holds by Proposition 3.3. By using (3.5), it can be easily verified that (3.34) holds, that is, all the entries of the matrix  are zero. Then
are zero. Then  for
for  , which is contrary to
, which is contrary to  for
for  . Hence,
. Hence,  is a simple eigenvalue of (1.1) and (1.2). This completes the proof.
is a simple eigenvalue of (1.1) and (1.2). This completes the proof.
Proposition 3.8.
Assume that  or
or  . If
. If  is odd,
is odd,  , and
, and  then
then  ; if
; if  is even,
is even,  , and
, and  then
then  for
for 
Proof.
We first prove the first result. Suppose that  is odd,
is odd,  , and
, and  . Then
. Then  is a multiple eigenvalue of (1.1) and (1.2) with
is a multiple eigenvalue of (1.1) and (1.2) with  by Proposition 3.6. Then by Proposition 3.3, (3.5) holds for
by Proposition 3.6. Then by Proposition 3.3, (3.5) holds for  and
and  , that is,
, that is,

Differentiating  with respect to
with respect to  two times, we get
two times, we get

Differentiating (2.14) with respect to  two times and from (3.40), we get
two times and from (3.40), we get

which, together with (3.41), implies that

On the other hand, it follows from (3.29) and (2.14) that, not indicating  explicitly,
explicitly,

Since  and
and  are linearly independent on
are linearly independent on  , the above relation implies that
, the above relation implies that  by Hölder's inequality, which proves the first conclusion.
by Hölder's inequality, which proves the first conclusion.
The second conclusion can be shown similarly. Hence, the proof is complete.
Finally, we turn to the proof of Theorem 3.1.
Proof of Theorem 3.1.
By Propositions 3.3–3.8, and the intermediate value theorem, one can obtain the graph of  (see Figure 1), which implies the results of Theorem 3.1. We now give its detailed proof.
(see Figure 1), which implies the results of Theorem 3.1. We now give its detailed proof.
By Propositions 3.3–3.6,  ,
,  for all
for all  with
with  and there exists
and there exists  such that
such that  Therefore, by the continuity of
Therefore, by the continuity of  and the intermediate value theorem, (1.1) and (1.2) with
and the intermediate value theorem, (1.1) and (1.2) with  has only one eigenvalue
has only one eigenvalue  , (1.1) and (1.2) with
, (1.1) and (1.2) with  has only one eigenvalue
has only one eigenvalue  , and (1.1) and (1.2) with
, and (1.1) and (1.2) with  ,
,  has only one eigenvalue
has only one eigenvalue  , and they satisfy
, and they satisfy

Similarly, by Propositions 3.3–3.6, the continuity of  and the intermediate value theorem,
and the intermediate value theorem,  reaches
reaches  ,
,  (
( ,
,  ), and
), and  exactly one time, respectively, between any two consecutive eigenvalues of the separated boundary value problem (1.1) with (2.7). Hence, (1.1) and (1.2) with
exactly one time, respectively, between any two consecutive eigenvalues of the separated boundary value problem (1.1) with (2.7). Hence, (1.1) and (1.2) with  ;
;  ,
,  ;
;  has only one eigenvalue between any two consecutive eigenvalues of (1.1) with (2.7), respectively. In addition, by Proposition 3.6, if
has only one eigenvalue between any two consecutive eigenvalues of (1.1) with (2.7), respectively. In addition, by Proposition 3.6, if  or
or  and
and  , then
, then  is not only an eigenvalue of (1.1) with (2.7) but also a multiple eigenvalue of (1.1) and (1.2) with
is not only an eigenvalue of (1.1) with (2.7) but also a multiple eigenvalue of (1.1) and (1.2) with  and
and  .
.
By Proposition 3.5 (i), if  is odd,
is odd,  and if
and if  is even,
is even,  . It follows (3.22) that if
. It follows (3.22) that if  is odd, then
is odd, then  as
as  and if
and if  is even, then
is even, then  as
as  . Hence, if
. Hence, if  is odd, then there exists a constant
is odd, then there exists a constant  such that
such that  , which, together with Proposition 3.6, implies that (1.1) and (1.2) with
, which, together with Proposition 3.6, implies that (1.1) and (1.2) with  ;
;  ,
,  ;
;  has only one eigenvalue
has only one eigenvalue  ,
,  , and
, and  , satisfying
, satisfying

(see Figure 2). Similarly, in the other case that  is even, there exists a constant
is even, there exists a constant  such that
such that  which, together with Proposition 3.6, implies that (1.1) and (1.2) with
which, together with Proposition 3.6, implies that (1.1) and (1.2) with  ;
;  ,
,  ;
;  has only one eigenvalue
has only one eigenvalue  ,
,  , and
, and  , satisfying
, satisfying

(see Figure 3). Therefore, we get that (1.1) and (1.2) with  ,
,  has
has  eigenvalues and it is real and satisfies
eigenvalues and it is real and satisfies

This completes the proof.
Remark 3.9.
Let  , that is,
, that is,  ,
,  . Then
. Then  . In this case, Propositions 3.5 and 3.8 are the same as those mentioned in [4, Propositions
. In this case, Propositions 3.5 and 3.8 are the same as those mentioned in [4, Propositions  , 3.3–3.5], respectively, and most of the results of Proposition 3.6 are the same as the results of [4, Proposition
, 3.3–3.5], respectively, and most of the results of Proposition 3.6 are the same as the results of [4, Proposition  ].
].
References
Atkinson FV: Discrete and Continuous Boundary Problems, Mathematics in Science and Engineering. Volume 8. Academic Press, New York, NY, USA; 1964:xiv+570.
Shi Y, Chen S: Spectral theory of second-order vector difference equations. Journal of Mathematical Analysis and Applications 1999,239(2):195–212. 10.1006/jmaa.1999.6510
Agarwal RP, Wong PJY: Advanced Topics in Difference Equations, Mathematics and Its Applications. Volume 404. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:viii+507.
Wang Y, Shi Y: Eigenvalues of second-order difference equations with periodic and antiperiodic boundary conditions. Journal of Mathematical Analysis and Applications 2005,309(1):56–69. 10.1016/j.jmaa.2004.12.010
Coddington EA, Levinson N: Theory of Ordinary Differential Equations. McGraw-Hill, New York, NY, USA; 1955:xii+429.
Hale JK: Ordinary Differential Equations, Pure and Applied Mathematics. Volume 20. Wiley-Interscience, New York, NY, USA; 1969:xvi+332.
Magnus W, Winkler S: Hill's Equation, Interscience Tracts in Pure and Applied Mathematics, no. 20. Wiley-Interscience, New York, NY, USA; 1966:viii+127.
Zhang M: The rotation number approach to eigenvalues of the one-dimensional -Laplacian with periodic potentials. Journal of the London Mathematical Society 2001,64(1):125–143. 10.1017/S0024610701002277
Agarwal RP, Bohner M, Wong PJY: Sturm-Liouville eigenvalue problems on time scales. Applied Mathematics and Computation 1999,99(2–3):153–166. 10.1016/S0096-3003(98)00004-6
Acknowledgments
Many thanks to Johnny Henderson (the editor) and the anonymous reviewers for helpful comments and suggestions. This research was supported by the Natural Scientific Foundation of Shandong Province (Grant Y2007A27), (Grant Y2008A28), and the Fund of Doctoral Program Research of University of Jinan (B0621).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, C., Sun, S. Inequalities among Eigenvalues of Second-Order Difference Equations with General Coupled Boundary Conditions. Adv Differ Equ 2009, 347291 (2009). https://doi.org/10.1155/2009/347291
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/347291
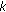 ,
,  ,
, 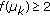 if
if  is odd, and
is odd, and 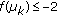 if
if  is even.
is even.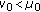 such that
such that  .
. eigenvalues then there exists a constant
eigenvalues then there exists a constant 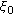 such that
such that  and
and  , where
, where 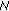 is odd, and there exists a constant
is odd, and there exists a constant  such that
such that 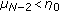 and
and 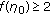 , where
, where 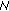 is even.
is even.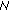 is odd,
is odd,  and if
and if 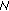 is even,
is even, 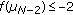 . By (3.22), if
. By (3.22), if  is odd,
is odd, 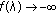 as
as 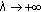 ; if
; if 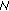 is even,
is even, 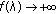 as
as 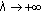 . Hence, if
. Hence, if  is odd, there exists a constant
is odd, there exists a constant  such that
such that  ; if
; if  is even, there exists a constant
is even, there exists a constant 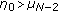 such that
such that  . This completes the proof.
. This completes the proof.
 .
.
 in the case that
in the case that  is odd.
is odd.
 in the case that
in the case that  is even.
is even.