- Research Article
- Open access
- Published:
Nonlinear Discrete Periodic Boundary Value Problems at Resonance
Advances in Difference Equations volume 2009, Article number: 360871 (2010)
Abstract
Let  be an integer with
be an integer with  , and let
, and let  . We study the existence of solutions of nonlinear discrete problems
. We study the existence of solutions of nonlinear discrete problems 
 ,
, 
 where
where  with
with  is the
is the  th eigenvalue of the corresponding linear eigenvalue problem.
th eigenvalue of the corresponding linear eigenvalue problem.
1. Introduction
Initialed by Lazer and Leach [1], much work has been devoted to the study of existence result for nonlinear periodic boundary value problem

where  is an integer. Results from the paper have been extended to partial differential equations by several authors. The reader is referred, for detail, to Landesman and Lazer [2], Amann et al. [3], Brézis and Nirenberg [4], Fučík and Hess [5], and Iannacci and Nkashama [6] for some reference along this line. Concerning (1.1), results have been carried out by many authors also. Let us mention articles by Mawhin and Ward [7], Conti et al. [8], Omari and Zanolin [9], Ding and Zanolin [10], Capietto and Liu [11], Iannacci and Nkashama [12], Chu et al. [13], and the references therein.
is an integer. Results from the paper have been extended to partial differential equations by several authors. The reader is referred, for detail, to Landesman and Lazer [2], Amann et al. [3], Brézis and Nirenberg [4], Fučík and Hess [5], and Iannacci and Nkashama [6] for some reference along this line. Concerning (1.1), results have been carried out by many authors also. Let us mention articles by Mawhin and Ward [7], Conti et al. [8], Omari and Zanolin [9], Ding and Zanolin [10], Capietto and Liu [11], Iannacci and Nkashama [12], Chu et al. [13], and the references therein.
However, relatively little is known about the discrete analog of (1.1) of the form

where  ,
,  with
with  ,
,  is continuous in
is continuous in  . The likely reason is that the spectrum theory of the corresponding linear problem
. The likely reason is that the spectrum theory of the corresponding linear problem

was not established until [14]. In [14], Wang and Shi showed that the linear eigenvalue problem (1.3) has exactly  real eigenvalues
real eigenvalues

Suppose that these above eigenvalues have  different values
different values  ,
,  . Then (1.4) can be rewritten as
. Then (1.4) can be rewritten as

For each  , we denote its eigenspace by
, we denote its eigenspace by  . If
. If  , then we assume that
, then we assume that  in which
in which  is the eigenfunction of
is the eigenfunction of  . If
. If  , then we assume that
, then we assume that  in which
in which  and
and  are two linearly independent eigenfunctions of
are two linearly independent eigenfunctions of  .
.
It is the purpose of this paper to prove the existence results for problem (1.2) when there occurs resonance at the eigenvalue  and the nonlinear function
and the nonlinear function  may "touching" the eigenvalue
may "touching" the eigenvalue  . To have the wit, we have what follows.
. To have the wit, we have what follows.
Theorem 1.1.
Let  with
with  ,
,  is continuous in
is continuous in  , and for some
, and for some  ,
,

where  are two given functions. Suppose for some
are two given functions. Suppose for some  ,
,

Assume that for all  , there exist a constant
, there exist a constant  and a function
and a function  such that
such that

where  is a given function satisfying
is a given function satisfying

and for at least  points in
points in  ,
,

where  denotes the integer part of the real number
denotes the integer part of the real number  .
.
Then (1.2) has at least one solution provided

where  ,
,  , and
, and

In [12], Iannacci and Nkashama proved the analogue of Theorem 1.1 for continuous-time nonlinear periodic boundary value problems (1.1). Our paper is motivated by Iannacci and Nkashama [12]. However, as we will see below, there are big differences between the continuous case and the discrete case. The main tool we use is the Leray-Schauder continuation theorem (see Mawhin [15, Theorem  ]).
]).
Finally, we note that when  in (1.2), the existence of odd solutions or even solutions was investigated by R. Ma and H. Ma [16] under some parity conditions on the nonlinearities. The existence of solutions of second-order discrete problem at resonance was studied by Rodriguez in [17], in which the nonlinearity is required to be bounded. For other results on discrete boundary value problems, see Kelley and Peterson [18], Agarwal and O'Regan [19], Rachunkova and Tisdell [20], Yu and Guo [21], Atici and Cabada [22], Bai and Xu [23]. However, these papers do not address the problem under "asymptotic nonuniform resonance" conditions.
in (1.2), the existence of odd solutions or even solutions was investigated by R. Ma and H. Ma [16] under some parity conditions on the nonlinearities. The existence of solutions of second-order discrete problem at resonance was studied by Rodriguez in [17], in which the nonlinearity is required to be bounded. For other results on discrete boundary value problems, see Kelley and Peterson [18], Agarwal and O'Regan [19], Rachunkova and Tisdell [20], Yu and Guo [21], Atici and Cabada [22], Bai and Xu [23]. However, these papers do not address the problem under "asymptotic nonuniform resonance" conditions.
2. Preliminaries
Let

Let

Then  is a Hilbert space under the inner product
is a Hilbert space under the inner product

and the corresponding norm is

Thus,

In the rest of the paper, we always assume that

Define a linear operator  by
by

Lemma 2.1 (see [16]).
Let  . Then
. Then

Similar to [12, Lemma  ], we can prove the following.
], we can prove the following.
Lemma 2.2 (see [12]).
Suppose that
-
(i)
there exist
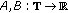 and real numbers
and real numbers  , such that
, such that

(ii) there exist  and a constant
and a constant  such that
such that

Then for each real number  , there is a decomposition
, there is a decomposition

of  satisfying
satisfying


and there exists a function  depending on
depending on  and
and  such that
such that

3. Existence of Periodic Solutions
In this section, we need to give some lemmas first, which have vital importance to prove Theorem 1.1.
For convenience, we set

Thus, for any  , we have the following Fourier expansion:
, we have the following Fourier expansion:

Let us write

where

Lemma 3.1.
Suppose that for  ,
,  is an eigenvalue of (1.3) of multiplicity 2. Let
is an eigenvalue of (1.3) of multiplicity 2. Let  be a given function satisfying
be a given function satisfying

and for at least  points in
points in  ,
,

Then there exists a constant  such that for all
such that for all  , one has
, one has

Proof.
For  ,
,

Taking into account the orthogonality of  ,
,  , and
, and  in
in  , we have
, we have

Set

Then,

where  is a positive constant less than
is a positive constant less than  .
.
Let

We claim that  with the equality holding only if
with the equality holding only if  , where
, where 
 are constants.
are constants.
In fact, we have from Lemma 2.1 that

Obviously,  implies that
implies that  , and accordingly
, and accordingly  for some
for some  .
.
Next we prove that  implies
implies  . Suppose to the contrary that
. Suppose to the contrary that  .
.
We note that  has at most
has at most  zeros in
zeros in  . Otherwise,
. Otherwise,  must have two consecutive zeros in
must have two consecutive zeros in  , and subsequently,
, and subsequently,  in
in  by (1.3). This is a contradiction.
by (1.3). This is a contradiction.
Using (3.6) and the fact that  has at most
has at most  zeros in
zeros in  , it follows that
, it follows that

which contradicts  . Hence,
. Hence,  .
.
We claim that there is a constant  such that
such that

Assume that the claim is not true. Then we can find a sequence  and
and  , such that, by passing to a subsequence if necessary,
, such that, by passing to a subsequence if necessary,


From (3.17), it follows that

By (3.12), (3.16), and (3.17), we obtain, for  ,
,

and hence

that is,

By the first part of the proof,  , so that, by (3.19),
, so that, by (3.19),  , a contradiction with the second equality in (3.16).
, a contradiction with the second equality in (3.16).
Set  and observing that
and observing that  the proof is complete.
the proof is complete.
Lemma 3.2.
Let  be as in Lemma 3.1 and let
be as in Lemma 3.1 and let  be associated with
be associated with  by that lemma. Let
by that lemma. Let  . Let
. Let  be a function satisfying
be a function satisfying

Then for all  , one has
, one has

Proof.
Using the computations in the proof of Lemma 3.1 and (3.22), we obtain

So that, using (3.7), (3.8), the relation  , and Lemma 2.1, it follows that
, and Lemma 2.1, it follows that

Proof of Theorem 1.1.
The proof is motivated by Iannacci and Nkashama [12].
Let  be associated to the function
be associated to the function  by Lemma 3.1. Then, by assumption (1.8), there exist
by Lemma 3.1. Then, by assumption (1.8), there exist  and
and  , such that
, such that

for all  and all
and all  with
with  . Hence, (1.2) is equivalent to
. Hence, (1.2) is equivalent to

where  and
and  satisfy (2.12) and (2.14) with
satisfy (2.12) and (2.14) with  . Moreover, by (2.13)
. Moreover, by (2.13)

Let  , so that
, so that

It follows from (3.28) and (3.29) that

Define  by
by

So we have

Define 

Then there exists  such that
such that

Therefore, (1.2) is equivalent to

To prove that (1.2) has at least one solution in  , it suffices, according to the Leray-Schauder continuation method [15], to show that all of the possible solutions of the family of equations
, it suffices, according to the Leray-Schauder continuation method [15], to show that all of the possible solutions of the family of equations

(in which  ,
,  with
with  ,
,  fixed) are bounded by a constant
fixed) are bounded by a constant  which is independent of
which is independent of  and
and  .
.
Notice that, by (3.32), we have

It is clear that for  , (3.36) has only the trivial solution. Now if
, (3.36) has only the trivial solution. Now if  is a solution of (3.36) for some
is a solution of (3.36) for some  , using Lemma 3.2 and Cauchy's inequality, we obtain
, using Lemma 3.2 and Cauchy's inequality, we obtain

where

So we conclude that

for some constant  , depending only on
, depending only on  and
and  (but not on
(but not on  or
or  ). Taking
). Taking  , we get
, we get

We claim that there exists  , independent of
, independent of  and
and  , such that for all possible solutions of (3.36)
, such that for all possible solutions of (3.36)

Suppose on the contrary that the claim is false. Then there exists 
 with
with  and for all
and for all  ,
,

From (3.41), it can be shown that

and accordingly,  is bounded in
is bounded in  .
.
Setting  , we have
, we have

Define an operator  by
by

Then  is completely continuous since
is completely continuous since  is finite dimensional. Now, (3.45) is equivalent to
is finite dimensional. Now, (3.45) is equivalent to

By (3.26), it follows that  is bounded. Using (3.47), we may assume that (taking a subsequence and relabeling if necessary)
is bounded. Using (3.47), we may assume that (taking a subsequence and relabeling if necessary)  in
in  ,
,  and
and  ,
,  .
.
On the other hand, using (3.41), we deduce immediately that

Therefore,

Rewrite  , and let, taking a subsequence and relabeling if necessary,
, and let, taking a subsequence and relabeling if necessary,

Set

Since  in
in  ,
,  or
or  .
.
We claim that


We may assume that  , and only deal with the case
, and only deal with the case  . The other case can be treated by similar method.
. The other case can be treated by similar method.
It follows from (3.50) that

which implies that for all  sufficiently large,
sufficiently large,

On the other hand, we have from (3.44), (3.55), and the fact  that there exists
that there exists  such that for
such that for  and
and  ,
,

This together with (3.55) implies that for  ,
,

Therefore, (3.52) holds.
Now let us come back to (3.43). Multiplying both sides of (3.43) by  and summing from
and summing from  to
to  , we get that
, we get that

Combining this with (3.52) and (3.53), it follows that

However, this contradicts (1.11).
Example 3.3.
By [16], the eigenvalues and eigenfunctions of

can be listed as follows:

Let us consider the nonlinear discrete periodic boundary value problem

where

Obviously,  ,
,  , and
, and  . If we take that
. If we take that

then

Now, it is easy to verify that  satisfies all conditions of Theorem 1.1. Consequently, for any
satisfies all conditions of Theorem 1.1. Consequently, for any  -periodic function
-periodic function  , (3.62) has at least one solution.
, (3.62) has at least one solution.
References
Lazer AC, Leach DE: Bounded perturbations of forced harmonic oscillators at resonance. Annali di Matematica Pura ed Applicata 1969, 82: 49–68. 10.1007/BF02410787
Landesman EM, Lazer AC: Nonlinear perturbations of linear elliptic boundary value problems at resonance. Journal of Applied Mathematics and Mechanics 1970, 19: 609–623.
Amann H, Ambrosetti A, Mancini G: Elliptic equations with noninvertible Fredholm linear part and bounded nonlinearities. Mathematische Zeitschrift 1978,158(2):179–194. 10.1007/BF01320867
Brézis H, Nirenberg L: Characterizations of the ranges of some nonlinear operators and applications to boundary value problems. Annali della Scuola Normale Superiore di Pisa 1978,5(2):225–326.
Fučík S, Hess P: Nonlinear perturbations of linear operators having nullspace with strong unique continuation property. Nonlinear Analysis 1979,3(2):271–277. 10.1016/0362-546X(79)90082-8
Iannacci R, Nkashama MN: Nonlinear boundary value problems at resonance. Nonlinear Analysis: Theory, Methods & Applications 1987,11(4):455–473. 10.1016/0362-546X(87)90064-2
Mawhin J, Ward JR Jr.: Periodic solutions of some forced Liénard differential equations at resonance. Archiv der Mathematik 1983,41(4):337–351. 10.1007/BF01371406
Conti G, Iannacci R, Nkashama MN: Periodic solutions of Liénard systems at resonance. Annali di Matematica Pura ed Applicata 1985, 139: 313–327. 10.1007/BF01766859
Omari P, Zanolin F: Existence results for forced nonlinear periodic BVPs at resonance. Annali di Matematica Pura ed Applicata 1985, 141: 127–157. 10.1007/BF01763171
Ding TR, Zanolin F: Time-maps for the solvability of periodically perturbed nonlinear Duffing equations. Nonlinear Analysis: Theory, Methods & Applications 1991,17(7):635–653. 10.1016/0362-546X(91)90111-D
Capietto A, Liu B: Quasi-periodic solutions of a forced asymmetric oscillator at resonance. Nonlinear Analysis: Theory, Methods & Applications 2004,56(1):105–117. 10.1016/j.na.2003.09.001
Iannacci R, Nkashama MN: Unbounded perturbations of forced second order ordinary differential equations at resonance. Journal of Differential Equations 1987,69(3):289–309. 10.1016/0022-0396(87)90121-5
Chu J, Torres PJ, Zhang M: Periodic solutions of second order non-autonomous singular dynamical systems. Journal of Differential Equations 2007,239(1):196–212. 10.1016/j.jde.2007.05.007
Wang Y, Shi Y: Eigenvalues of second-order difference equations with periodic and antiperiodic boundary conditions. Journal of Mathematical Analysis and Applications 2005,309(1):56–69. 10.1016/j.jmaa.2004.12.010
Mawhin J: Topological Degree Methods in Nonlinear Boundary Value Problems, CBMS Regional Conference Series in Mathematics. Volume 40. American Mathematical Society, Providence, RI, USA; 1979:v+122.
Ma R, Ma H: Unbounded perturbations of nonlinear discrete periodic problem at resonance. Nonlinear Analysis: Theory, Methods & Applications 2009,70(7):2602–2613. 10.1016/j.na.2008.03.047
Rodriguez J: Nonlinear discrete Sturm-Liouville problems. Journal of Mathematical Analysis and Applications 2005,308(1):380–391. 10.1016/j.jmaa.2005.01.032
Kelley WG, Peterson AC: Difference Equations. Academic Press, Boston, Mass, USA; 1991:xii+455.
Agarwal RP, O'Regan D: Boundary value problems for discrete equations. Applied Mathematics Letters 1997,10(4):83–89. 10.1016/S0893-9659(97)00064-5
Rachunkova I, Tisdell CC: Existence of non-spurious solutions to discrete Dirichlet problems with lower and upper solutions. Nonlinear Analysis: Theory, Methods & Applications 2007,67(4):1236–1245. 10.1016/j.na.2006.07.010
Yu J, Guo Z: On boundary value problems for a discrete generalized Emden-Fowler equation. Journal of Differential Equations 2006,231(1):18–31. 10.1016/j.jde.2006.08.011
Atici FM, Cabada A: Existence and uniqueness results for discrete second-order periodic boundary value problems. Computers & Mathematics with Applications 2003,45(6–9):1417–1427.
Bai D, Xu Y: Nontrivial solutions of boundary value problems of second-order difference equations. Journal of Mathematical Analysis and Applications 2007,326(1):297–302. 10.1016/j.jmaa.2006.02.091
Acknowledgments
This work was supported by the NSFC (no. 10671158), the NSF of Gansu Province (no. 3ZS051-A25-016), NWNU-KJCXGC-03-17, NWNU-KJCXGC-03-18, the Spring-Sun program (no. Z2004-1-62033), SRFDP (no. 20060736001), and the SRF for ROCS, SEM (2006 [ ]).
]).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, R., Ma, H. Nonlinear Discrete Periodic Boundary Value Problems at Resonance. Adv Differ Equ 2009, 360871 (2010). https://doi.org/10.1155/2009/360871
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/360871
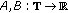 and real numbers
and real numbers  , such that
, such that