- Research Article
- Open access
- Published:
Banded Matrices and Discrete Sturm-Liouville Eigenvalue Problems
Advances in Difference Equations volume 2009, Article number: 362627 (2010)
Abstract
We consider eigenvalue problems for self-adjoint Sturm-Liouville difference equations of any even order. It is well known that such problems with Dirichlet boundary conditions can be transformed into an algebraic eigenvalue problem for a banded, real-symmetric matrix, and vice versa. In this article it is shown that such a transform exists for general separated, self-adjoint boundary conditions also. But the main result is an explicit procedure (algorithm) for the numerical computation of this banded, real-symmetric matrix. This construction can be used for numerical purposes, since in the recent paper by Kratz and Tentler (2008) there is given a stable and superfast algorithm to compute the eigenvalues of banded, real-symmetric matrices. Hence, the Sturm-Liouville problems considered here may now be treated by this algorithm.
1. Introduction
In [1] it was shown that every discrete Sturm-Liouville eigenvalue problem (where  )
)

with Dirichlet boundary conditions  is equivalent with an algebraic eigenvalue problem [2] for a symmetric, banded
is equivalent with an algebraic eigenvalue problem [2] for a symmetric, banded  -matrix with bandwidth
-matrix with bandwidth  , where
, where  and
and  are fixed integers with
are fixed integers with  (see [1, Theorem 1, Remark 1(i)]). Note that (SL) is irrelevant for
(see [1, Theorem 1, Remark 1(i)]). Note that (SL) is irrelevant for  in the case of Dirichlet boundary conditions, so that in [1] equation (SL) is considered only for
in the case of Dirichlet boundary conditions, so that in [1] equation (SL) is considered only for  .
.
In this article we treat the Sturm-Liouville difference equations (SL) with general separated, self-adjoint boundary conditions. These boundary conditions include the so-called natural boundary conditions, when no or "not enough'' boundary conditions are imposed [3, page 51, equation (2.3.9)]. More precisely, given (SL) and the (imposed and natural) boundary conditions, then we show that this eigenvalue problem is equivalent with an algebraic eigenvalue problem for a real-symmetric, banded matrix with bandwidth  , and we will construct this matrix explicity. For our general boundary conditions we must assume that the coefficients
, and we will construct this matrix explicity. For our general boundary conditions we must assume that the coefficients  are unequal to zero at "the beginning and at the end'' (see (4.7) below). This leads via [4] or [5] to a numerical algorithm to compute the eigenvalues of these Sturm-Liouville eigenvalue problems.
are unequal to zero at "the beginning and at the end'' (see (4.7) below). This leads via [4] or [5] to a numerical algorithm to compute the eigenvalues of these Sturm-Liouville eigenvalue problems.
Therefore the present paper is to some extent a continuation of the articles [1, 4]. The paper [4] presents superfast (i.e., with  numerical operations) and stable algorithms for the computation of some of the eigenvalues for a real-symmetric and banded
numerical operations) and stable algorithms for the computation of some of the eigenvalues for a real-symmetric and banded  matrix with bandwidth
matrix with bandwidth  , where
, where  or
or  for the most interesting division-free algorithms. These algorithms are based on the bisection method, and they generalize the well-known procedure for real-symmetric and tridiagonal matrices. As is shown in [1] and used in [4] the algebraic eigenvalue problems for real-symmetric, banded matrices with bandwidth
for the most interesting division-free algorithms. These algorithms are based on the bisection method, and they generalize the well-known procedure for real-symmetric and tridiagonal matrices. As is shown in [1] and used in [4] the algebraic eigenvalue problems for real-symmetric, banded matrices with bandwidth  are equivalent to eigenvalue problems for self-adjoint Sturm-Liouville difference equations of order
are equivalent to eigenvalue problems for self-adjoint Sturm-Liouville difference equations of order  with Dirichlet boundary conditions. Hence, these discrete Sturm-Liouville eigenvalue problems can be treated by those algorithms.
with Dirichlet boundary conditions. Hence, these discrete Sturm-Liouville eigenvalue problems can be treated by those algorithms.
Summarizing, the main goal of this article is to provide an algorithm to calculate some of the eigenvalues of eigenvalue problems for self-adjoint Sturm-Liouville difference equations with general separated, self-adjoint boundary conditions (and not only for Dirichlet conditions as in [4, 5]). To be more precise, we provide a construction to transform these eigenvalue problems into such eigenvalue problems with Dirichlet boundary conditions. This construction incorporates "somehow'' the general boundary conditions into the first and last  equations of the Sturm-Liouville difference equations. These transformations are stable (using essentially orthogonal transforms) and the required computational work depends on
equations of the Sturm-Liouville difference equations. These transformations are stable (using essentially orthogonal transforms) and the required computational work depends on  only (most interesting
only (most interesting  ) but not on
) but not on  , so that the overall combined (with [4]) algorithm remains superfast (i.e., O(
, so that the overall combined (with [4]) algorithm remains superfast (i.e., O( ) numerical operations) and stable. Hence, the results of this paper are of interest mainly for numerical applications.
) numerical operations) and stable. Hence, the results of this paper are of interest mainly for numerical applications.
Because of our intention above this article, more precisely Sections 2 to 5 of it, consists essentially of the following central parts:
-
(i)
deriving the transform to an explicit algebraic algebraic eigenvalue problem for a symmetric, banded matrix with bandwidth
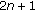 ,
, -
(ii)
providing the required formulas, so that an implementation of the construction is easily "accessible'' for the reader,
-
(iii)
proving that the construction is always successful under the conditions (4.4) and (4.7) (which is the contents of Theorem 6.1).
This means that Sections 2 to 5 have to be quite technical. Our proceeding in these sections provides simultaneously the construction, the derivation, and the proof that the construction always works.
As already said the asserted equivalence in Theorem 6.1 is not the crucial result of this article. Actually, under the assumptions (4.4) and (4.7) this equivalence may be shown quite easily using Lemma 2.3 and Proposition 3.2. Moreover, assumption (4.4) is necessary and sufficient for self-adjointness (see, e.g., [3, Proposition 2.1.1] or elsewhere), if (4.7) holds. The assumption (4.7) is also necessary for all considered boundary conditions simultaneously, but for a particular boundary condition it may be weakened. But this can be seen during the procedure. The equivalence via Lemma 2.3 and Proposition 3.2 directly leads in general to a banded symmetric matrix with larger bandwidth. On the other hand the "minimal bandwidth'' tridiagonal (i.e.,  ) can always be achieved in a stable way by the well-known methods of Givens and Householder, but these algorithms require
) can always be achieved in a stable way by the well-known methods of Givens and Householder, but these algorithms require  numerical operations as discussed in [4], which would make our whole approach obsolete.
numerical operations as discussed in [4], which would make our whole approach obsolete.
Note that our main goal is equivalence to an "ordinary'' algebraic eigenvalue problem for a real-symmetric and banded matric rather than to some matrix pencil or generalized eigenvalue problem of the form  . This is so, because the algorithm via bisection works only for these algebraic eigenvalue problems, which are well posed, while those general problems are in general not well posed. Note also that the equivalence to "some matrix pencil'' can be seen immediately from (SL) or (4.1) and also (4.2). Moreover, the reduction of separated boundary conditions to Dirichlet boundary conditions via an extension of the system to a larger interval is also well known for discrete Hamiltonian or symplectic systems (see, e.g., [6] or [7]). Hence, this reduction combined with the transformation of the Sturm-Liouville equations (SL) to a linear Hamiltonian system by Lemma 2.2 would also lead to a problem with Dirichlet boundary conditions but for a larger matrix, more precisely, it would lead to some matrix pencil (possible also with larger bandwidth), which cannot be treated by the algorithms of [4, 5].
. This is so, because the algorithm via bisection works only for these algebraic eigenvalue problems, which are well posed, while those general problems are in general not well posed. Note also that the equivalence to "some matrix pencil'' can be seen immediately from (SL) or (4.1) and also (4.2). Moreover, the reduction of separated boundary conditions to Dirichlet boundary conditions via an extension of the system to a larger interval is also well known for discrete Hamiltonian or symplectic systems (see, e.g., [6] or [7]). Hence, this reduction combined with the transformation of the Sturm-Liouville equations (SL) to a linear Hamiltonian system by Lemma 2.2 would also lead to a problem with Dirichlet boundary conditions but for a larger matrix, more precisely, it would lead to some matrix pencil (possible also with larger bandwidth), which cannot be treated by the algorithms of [4, 5].
The discussion of assumption (4.7) in the Concluding Remarks of Section 6 does not focus on the necessity or sufficiency of it. It is quite "natural'' to assume that the leading coefficient  never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the the difference equations by our construction leads in general to problems with Dirichlet boundary conditions, but where the leading coefficient may vanish for some
never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the the difference equations by our construction leads in general to problems with Dirichlet boundary conditions, but where the leading coefficient may vanish for some  's at the beginning and the end. Therefore, algorithms via corresponding Hamiltonian or Riccati equations cannot be used anymore, so that the division-free algorithms (i.e., no divisions by
's at the beginning and the end. Therefore, algorithms via corresponding Hamiltonian or Riccati equations cannot be used anymore, so that the division-free algorithms (i.e., no divisions by  ) are needed as remarked in Concluding Remarks (i) of Section 6.
) are needed as remarked in Concluding Remarks (i) of Section 6.
Let us shortly motivate why to consider the discrete Sturm-Liouville eigenvalue problems of this article, particularly for  and
and  , and for general boundary conditions.
, and for general boundary conditions.
-
(i)
The discretization of a second order Sturm-Liouville equation
 (1.1)
(1.1)of higher order leads to a banded matrix with bandwidth
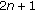 with
with 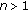 , and then even Dirichlet boundary conditions
, and then even Dirichlet boundary conditions  lead for the discrete problem to the boundary conditions
lead for the discrete problem to the boundary conditions  , which have to be complemented by additional "natural boundary conditions'' in the usual way. Therefore, such problems of second order with Dirichlet boundary conditions cannot be treated (at least for higher-order discretization) directly by the algorithm of [4]. By using the construction of this article we obtain faster algorithms than the known ones.
, which have to be complemented by additional "natural boundary conditions'' in the usual way. Therefore, such problems of second order with Dirichlet boundary conditions cannot be treated (at least for higher-order discretization) directly by the algorithm of [4]. By using the construction of this article we obtain faster algorithms than the known ones. -
(ii)
Linear discretization of
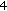 th- and
th- and 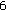 th-order Sturm-Liouville difference equations leads to bandwidths
th-order Sturm-Liouville difference equations leads to bandwidths 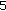 and
and  , and the numerical treatment of Dirichlet boundary conditions via [4] requires also the construction of this article.
, and the numerical treatment of Dirichlet boundary conditions via [4] requires also the construction of this article.
Let us shortly discuss the setup of this paper. In the next section we provide the formulae, which transform the difference equations (SL) into the corresponding matrix equation (see Lemma 2.1 below) based on [1]. In Section 3 we derive via partial summation the so-called Dirichlet's formula, which yields the crucial identities (3.3). In Section 4 we formulate our discrete Sturm-Liouville eigenvalue problems. In particular, we introduce (based on [8]) and discuss shortly the corresponding general separated, self-adjoint boundary conditions. In Section 5 we carry out our construction of the symmetric, banded matrix, so that the corresponding algebraic eigenvalue problem is equivalent with our Sturm-Liouville problem. Hence, our proceeding in Sections 2 to 5 provides simultaneously the construction, the derivation, and the proof that the construction always works. This is formulated as our main result in the last Section 6 by adding some concluding remarks.
2. Discrete Sturm-Liouville Difference Equations, Banded Matrices, and Hamiltonian Systems
Let  , and let reals
, and let reals  for
for  and
and  be given. Then, for
be given. Then, for  , we consider the Sturm-Liouville difference operator
, we consider the Sturm-Liouville difference operator  defined by
defined by

where  is the forward difference operator, that is,
is the forward difference operator, that is,  , which will always operate with respect to the variable
, which will always operate with respect to the variable  . Then, by [1, Theorem 1], we have that
. Then, by [1, Theorem 1], we have that

where  is a symmetric, banded matrix with bandwidth
is a symmetric, banded matrix with bandwidth  , given by
, given by

for  and all
and all  .
.
This formula yields the following.
Lemma 2.1.
For  and
and  define vectors
define vectors

Then,

where  is a symmetric matrix, and where
is a symmetric matrix, and where

is lower triangular, and it is invertible, if  for
for  . Moreover, the equation
. Moreover, the equation

is equivalent with

Next, we have by [1, Lemma 3] or [9, Remark 2] the following.
Lemma 2.2.
For  and
and  define vectors
define vectors

Then, for any  , the equation
, the equation

is equivalent with the Hamiltonian system

provided that  , where one uses the following notation:
, where one uses the following notation:  ,
,  ,
,  ,
,  are
are  -matrices defined by
-matrices defined by

For the next lemma; see, for example, [10, formulae ( 6) and ( 9)] for the case of constant coefficients. It follows easily from our formulae (2.4) and (2.9) by computing the finite differences via  .
.
Lemma 2.3.
Let  (correspondly
(correspondly  ),
),  , and
, and  be defined by (2.4) and (2.9). Then,
be defined by (2.4) and (2.9). Then,

where  is invertible with
is invertible with  , and where
, and where  ,
,  are
are  -matrices with
-matrices with

and  is invertible, if
is invertible, if  for
for  .
.
3. Dirichlet's Formula
The next lemma is a discrete version of the continuous Dirichlet's formula [3, Lemma 8.4.3].
Lemma 3.1.
For  and two sequences
and two sequences  ,
,  let the operator
let the operator  , the vectors
, the vectors  ,
,  ,
,  ,
,  , and the matrices
, and the matrices  and
and  be defined as in the previous section by (2.1) and Lemma 2.2. Then, for any
be defined as in the previous section by (2.1) and Lemma 2.2. Then, for any  ,
,

Proof.
A straight forward calculation using (2.1) and (2.9) yields

which proves our assertion (3.1) using also the definition of  and
and  by Lemma 2.2.
by Lemma 2.2.
Proposition 3.2.
The matrices  ,
,  ,
,  , and
, and  from Lemmas 2.3 and 2.1 satisfy
from Lemmas 2.3 and 2.1 satisfy

Proof.
We consider the functional  , with
, with  and
and  defined by (2.4) of Lemma 2.1, where we put
defined by (2.4) of Lemma 2.1, where we put  . Then, by (2.5) of Lemma 2.1 we have that
. Then, by (2.5) of Lemma 2.1 we have that

From the definition of  by (2.4) and Dirichlet's formula (3.1) we obtain that
by (2.4) and Dirichlet's formula (3.1) we obtain that

where  is a symmetric matrix. Comparing this last formula (observe that
is a symmetric matrix. Comparing this last formula (observe that  ,
,  ,
,  are completely free) with (3.4) we can conclude that
are completely free) with (3.4) we can conclude that

because  is symmetric by Lemma 2.1. This yields our assertion (3.3).
is symmetric by Lemma 2.1. This yields our assertion (3.3).
4. Discrete Sturm-Liouville Eigenvalue Problems with Separated, Self-Adjoint Boundary Conditions
Let integers  with
with  (see (5.4) below) and real coefficients
(see (5.4) below) and real coefficients  be given. Then, we consider the following discrete eigenvalue problem, which we will denote by
be given. Then, we consider the following discrete eigenvalue problem, which we will denote by  . It consists of the
. It consists of the  self-adjoint Sturm-Liouville difference equations of even order
self-adjoint Sturm-Liouville difference equations of even order  (see (SL), Lemmas 2.1 and 2.2 above):
(see (SL), Lemmas 2.1 and 2.2 above):

and it consists of the  linearly independent, separated, and self-adjoint boundary conditions
linearly independent, separated, and self-adjoint boundary conditions

at the beginning, and

at the end, where  ,
,  ,
,  ,
,  are defined by (2.9) of Lemma 2.2, and where the real
are defined by (2.9) of Lemma 2.2, and where the real  -matrices
-matrices  ,
,  ,
,  ,
,  satisfy the following conditions:
satisfy the following conditions:

By Lemma 2.3, (4.2) and (4.3) lead to the following equivalent conditions on  ,
,  ,
,  ,
,  , defined by (2.4), that is, on
, defined by (2.4), that is, on  and on
and on  ,
,  , respectively:
, respectively:


where  ,
,  , and where
, and where  ,
,  ,
,  are defined by Lemma 2.3. Moreover, the equivalence of (4.2), (4.3) with (4.5), (4.6) requires the assumption that
are defined by Lemma 2.3. Moreover, the equivalence of (4.2), (4.3) with (4.5), (4.6) requires the assumption that  and
and  are invertible, which means by Lemma 2.3 that
are invertible, which means by Lemma 2.3 that

We assume this from now on.
The self-adjointness of  follows from general theory of linear Hamiltonian difference systems [11], and from the equivalence of our difference equation (4.1) with such systems, which is stated in Lemma 2.2. In addition, the self-adjointness of the boundary conditions via the assumption (4.4) is stated or discussed, for example, in [3, Definition 2.1.2], [8, Remark 2(iii)], [12, Proposition 2], or [7, Definition 1].
follows from general theory of linear Hamiltonian difference systems [11], and from the equivalence of our difference equation (4.1) with such systems, which is stated in Lemma 2.2. In addition, the self-adjointness of the boundary conditions via the assumption (4.4) is stated or discussed, for example, in [3, Definition 2.1.2], [8, Remark 2(iii)], [12, Proposition 2], or [7, Definition 1].
5. Construction of the Symmetric, Banded Matrix
First, by Lemma 2.1, the Sturm-Liouville difference equations (4.1) may be written in matrix notation, namely,

where the coefficient matrix is of the form

which is  , and where
, and where

and where we have written the first  and the last
and the last  rows of
rows of  in blocked form according to (2.4) and (2.5) of Lemma 2.1. It is the aim of this section to incorporate the boundary conditions (4.2) or (4.5) and (4.3) or (4.6) into the first
in blocked form according to (2.4) and (2.5) of Lemma 2.1. It is the aim of this section to incorporate the boundary conditions (4.2) or (4.5) and (4.3) or (4.6) into the first  and the last
and the last  equations of (4.1), that is, the first and last block rows of
equations of (4.1), that is, the first and last block rows of  , respectively. This requires in general that
, respectively. This requires in general that

As a result we will obtain an algebraic eigenvalue problem for a symmetric, banded matrix of size  with integers
with integers  depending on the boundary conditions. This algebraic eigenvalue problem will be equivalent with our given Sturm-Liouville eigenvalue problem
depending on the boundary conditions. This algebraic eigenvalue problem will be equivalent with our given Sturm-Liouville eigenvalue problem  from Section 4 under the assumptions (4.4) and (4.7).
from Section 4 under the assumptions (4.4) and (4.7).
5.1. Boundary Conditions at the Beginning
We consider the boundary conditions (4.2) or (4.5) at the beginning by assuming (4.4) and (4.7). Hence,  and
and  are invertible by Lemmas 2.1 and 2.3. Let
are invertible by Lemmas 2.1 and 2.3. Let  ,
,  be real
be real  -matrices such that (see (4.5))
-matrices such that (see (4.5))

where  ,
,  The existence (including construction) follows from [3, Corollary 3.3.9], because
The existence (including construction) follows from [3, Corollary 3.3.9], because

holds. This follows from (4.4) and (4.5) by the calculations

is symmetric, where we used (3.3) of Proposition 3.2. Moreover, (C1) and (5.5) imply by [3, Proposition 1.1.5] that

We conclude from (C1) and (5.7) that our boundary conditions (4.2) or (4.5) are equivalent with

Since  is real-symmetric by (5.7), there exists by the spectral theorem [13] an orthogonal matrix
is real-symmetric by (5.7), there exists by the spectral theorem [13] an orthogonal matrix  such that
such that

where  is diagonal and invertible, so that
is diagonal and invertible, so that

We use this block structure from now on including the extreme cases  and
and  , where the zero-matrices or
, where the zero-matrices or  do not occur. By the Gram-Schmidt process (or QR-factorization [13]), there exists an orthogonal matrix
do not occur. By the Gram-Schmidt process (or QR-factorization [13]), there exists an orthogonal matrix  such that
such that  is lower triangular, where
is lower triangular, where  with the blockstructure above, that is,
with the blockstructure above, that is,  . Then
. Then  is orthogonal, and
is orthogonal, and

where  is symmetric and invertible. Let
is symmetric and invertible. Let

By (5.5) and (C1),  , and
, and

is symmetric. Hence,  , because
, because  is invertible, and
is invertible, and  , so that
, so that  is invertible.
is invertible.
Altogether, we have constructed  such that
such that

with a symmetric and invertible matrix  , where
, where  ,
,

with an invertible matrix  and so that
and so that  is symmetric, and
is symmetric, and

so that  is lower triangular, and where
is lower triangular, and where  is orthogonal.
is orthogonal.
It follows immediately from (C1) and (C2) that our boundary conditions (4.2) or (4.5) are equivalent with

and therefore with

where

with  while
while  and
and  remain free.
remain free.
We say that (5.18) is the boundary conditions in normalized form.
Now, we consider the first equations or the first block row of our difference equations (4.1) or (5.1), that is, by Lemma 2.1 and (5.2),
equations or the first block row of our difference equations (4.1) or (5.1), that is, by Lemma 2.1 and (5.2),

We obtain from (5.7) and (5.8) that

Hence, under (5.8) (i.e., the boundary conditions), (5.19) is equivalent with (use also the notation of (5.18) and (C2))

where  is symmetric by Lemma 2.1 and (5.7). Hence, by (C2), equation (5.19) is equivalent with (under the boundary conditions (5.18))
is symmetric by Lemma 2.1 and (5.7). Hence, by (C2), equation (5.19) is equivalent with (under the boundary conditions (5.18))


Now, (5.22) defines independently of
independently of  , which was free by (5.18). Note that
, which was free by (5.18). Note that  is symmetric, because
is symmetric, because  and
and  are symmetric by Lemma 2.1 and (5.7). Moreover,
are symmetric by Lemma 2.1 and (5.7). Moreover,  is lower triangular by (C2), so that (5.23) leads to bandwidth
is lower triangular by (C2), so that (5.23) leads to bandwidth  and symmetry. More precisely, we drop the first
and symmetry. More precisely, we drop the first  columns of
columns of  , and the first
, and the first  rows are replaced by the following rows, which constitute the first
rows are replaced by the following rows, which constitute the first rows of the symmetric, banded matrix under construction:
rows of the symmetric, banded matrix under construction:

and where  .
.
The next  equations of (4.1) are given by
equations of (4.1) are given by

where  by (C2), because
by (C2), because  by (5.18). Hence, the next
by (5.18). Hence, the next rows from
rows from  of our matrix under construction have to be defined by
of our matrix under construction have to be defined by

This completes the construction concerning the boundary conditions at the beginning. Thus, possible eigenvectors have to be of the form  , where the boundary conditions are satisfied by putting
, where the boundary conditions are satisfied by putting  and defining
and defining  and
and  by (5.18) and (5.22), respectively.
by (5.18) and (5.22), respectively.
5.2. Boundary Conditions at the End
We proceed similarly as in the previous subsection. Therefore, we can skip some details. We shall use for convenience the same notation for auxiliary matrices or vectors here, but of course, with a different meaning. Observe that the situation is nevertheless not symmetric (see the concluding remarks (ii) below).
We consider the boundary conditions (4.3) or (4.6) at the end by assuming (4.4) and (4.7), so that  and
and  are invertible. Let
are invertible. Let  ,
,  be real
be real  -matrices such that (see (4.6))
-matrices such that (see (4.6))

where  ,
,  .
.
These matrices exist, because (5.5) holds by (4.4) and (4.6). Note that

by Proposition 3.2 and (4.6). Moreover, (5.7) holds as before. Hence, the boundary conditions (4.3) or (4.6) are equivalent with

By the spectral theorem there exists an orthogonal matrix  such that
such that

where  is diagonal and invertible, so that
is diagonal and invertible, so that

As before we use this block structure including the extreme cases  and
and  . By QR-factorization there exists an orthogonal matrix
. By QR-factorization there exists an orthogonal matrix  such that
such that  is upper triangular, where
is upper triangular, where  with the blockstructure above, that is,
with the blockstructure above, that is,  . Then
. Then  is orthogonal, and
is orthogonal, and

where  is symmetric and invertible. Let
is symmetric and invertible. Let

By (5.5) and (C5) we obtain that  and that
and that  is invertible.
is invertible.
Altogether, we have constructed  such that
such that

with a symmetric and invertible matrix  , where
, where  ,
,

with an invertible matrix  and so that
and so that  is symmetric, and
is symmetric, and

so that  is upper triangular, and where
is upper triangular, and where  is orthogonal.
is orthogonal.
It follows from (C5) and (C6) that our boundary conditions (4.3) or (4.6) or (5.26) are equivalent with

and therefore with

with  ,
,  ,
,  , and
, and  remaining free. We say that (5.34) is the boundary conditions (at the end) in normalized form.
remaining free. We say that (5.34) is the boundary conditions (at the end) in normalized form.
Next, we consider the last equations of our difference equations (4.1) or (5.1), that is, by Lemma 2.1 and (5.2),
equations of our difference equations (4.1) or (5.1), that is, by Lemma 2.1 and (5.2),

Then, under (5.34) (i.e., the boundary conditions) this is equivalent with (using the notation of (5.34) and (C6))

that is

where  is symmetric by Lemma 2.1. Hence, by (C6), equation (5.35) is equivalent with (under the boundary conditions (5.34))
is symmetric by Lemma 2.1. Hence, by (C6), equation (5.35) is equivalent with (under the boundary conditions (5.34))


Now, (5.38) defines independently of
independently of  , which was free by (5.34). Note that
, which was free by (5.34). Note that  is symmetric, because
is symmetric, because  is symmetric by Lemma 2.1 and because
is symmetric by Lemma 2.1 and because  is symmetric by (C6). Moreover,
is symmetric by (C6). Moreover,  is upper triangular by (C6), so that (5.39) leads to bandwidth
is upper triangular by (C6), so that (5.39) leads to bandwidth  and symmetry. More precisely, we drop the last
and symmetry. More precisely, we drop the last  columns of
columns of  , and the last
, and the last  rows are replaced by the following rows, which constitute the last
rows are replaced by the following rows, which constitute the last rows of the symmetric, banded matrix under construction:
rows of the symmetric, banded matrix under construction:

and where 
The last but one  equations of (4.1) are given by
equations of (4.1) are given by

Note that for  this overlaps with (5.24) of the previous subsection, and
this overlaps with (5.24) of the previous subsection, and  may have been changed by the construction there. We use here this new
may have been changed by the construction there. We use here this new  from Section 5.1, but note that it is irrelevant here. By (C6) and (5.34) we have that
from Section 5.1, but note that it is irrelevant here. By (C6) and (5.34) we have that

Hence, the  rows before the
rows before the  rows of (C7) of our matrix under construction have to be defined by
rows of (C7) of our matrix under construction have to be defined by

This completes the construction. Thus, possible eigenvectors must be of the form

6. Main Result and Concluding Remarks
Altogether we have shown by the construction of Section 5 the following result.
Theorem 6.1.
Assume (4.4) and (4.7). Then the construction of Section 5 transforms the Sturm-Liouville eigenvalue problem  (given by (4.1) and (4.2)) of Section 4 into an equivalent algebraic eigenvalue problem for a real-symmetric, banded matrix with bandwidth
(given by (4.1) and (4.2)) of Section 4 into an equivalent algebraic eigenvalue problem for a real-symmetric, banded matrix with bandwidth  . This matrix is of size
. This matrix is of size  with
with  given by (5.10) and (5.28), and it is constructed from
given by (5.10) and (5.28), and it is constructed from  (defined by (5.2)) by (C1)–(C8).
(defined by (5.2)) by (C1)–(C8).
Concluding Remarks
-
(i)
By our theorem every discrete Sturm-Liouville eigenvalue problem
 is equivalent with an algebraic eigenvalue problem for a banded, symmetric matrix under the assumptions (4.4) and (4.7). On the other hand, by [1, Remark 1(i)], such an algebraic eigenvalue problem is equivalent with a discrete Sturm-Liouville eigenvalue problem with Dirichlet boundary conditions. Moreover, if
is equivalent with an algebraic eigenvalue problem for a banded, symmetric matrix under the assumptions (4.4) and (4.7). On the other hand, by [1, Remark 1(i)], such an algebraic eigenvalue problem is equivalent with a discrete Sturm-Liouville eigenvalue problem with Dirichlet boundary conditions. Moreover, if  for all
for all  , then our eigenvalue problem
, then our eigenvalue problem  can be written as an eigenvalue problem for a corresponding Hamiltonian system or symplectic system [14] according to Lemma 2.2. Note that it is quite natural to assume that the leading coefficient
can be written as an eigenvalue problem for a corresponding Hamiltonian system or symplectic system [14] according to Lemma 2.2. Note that it is quite natural to assume that the leading coefficient 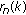 never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the difference equations by our construction leads in general to a problem where the leading coefficient may vanish for some
never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the difference equations by our construction leads in general to a problem where the leading coefficient may vanish for some 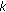 's at the beginning and the end. To be more precise, our construction may cause that matrix elements
's at the beginning and the end. To be more precise, our construction may cause that matrix elements  become zero at the beginning and at the end, so that its equivalent Sturm-Liouville problem with Dirichlet boundary conditions will not satisfy
become zero at the beginning and at the end, so that its equivalent Sturm-Liouville problem with Dirichlet boundary conditions will not satisfy for all
for all  anymore, because
anymore, because 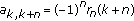 by (2.3). Hence, it cannot be written as an eigenvalue problem for a linear Hamiltonian difference system, so that the corresponding recursion formulae (based on the Hamiltonian or associated Riccati difference system [4, 11]) cannot be applied for numerical purposes as in [4, Theorems A and 2]. Therefore, divisions by
by (2.3). Hence, it cannot be written as an eigenvalue problem for a linear Hamiltonian difference system, so that the corresponding recursion formulae (based on the Hamiltonian or associated Riccati difference system [4, 11]) cannot be applied for numerical purposes as in [4, Theorems A and 2]. Therefore, divisions by  must be avoided, which is done by the division-free algorithms presented in [4, 5]. Hence, these division-free algorithms are crucial for our purposes.
must be avoided, which is done by the division-free algorithms presented in [4, 5]. Hence, these division-free algorithms are crucial for our purposes. -
(ii)
Note that in contrast to the corresponding continuous Sturm-Liouville problems (or the corresponding Hamiltonian differential systems), there is no symmetry with respect to the endpoints in the discrete case. This is quite obvious by the difference equation (4.1) with forward differences. Therefore the treatment of the boundary conditions at the endpoints in the subsections above had to be done separately. Actually the results of this treatment are quite different as can be seen also from the next remark.
-
(iii)
We discuss the extreme cases
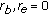 or
or  of our construction. It follows from (5.10) and (5.28) that
of our construction. It follows from (5.10) and (5.28) that  if and only if
if and only if 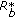 is invertible, that is,
is invertible, that is,  by (4.5) (this includes Dirichlet conditions
by (4.5) (this includes Dirichlet conditions for
for  ).
).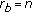 if and only if
if and only if  , that is,
, that is,  by (4.5) (so that
by (4.5) (so that  or
or 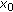 is free).
is free).  if and only if
if and only if 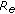 or
or  is invertible, that is,
is invertible, that is,  by (4.6) or
by (4.6) or  by (4.3) (this includes natural boundary conditions
by (4.3) (this includes natural boundary conditions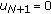 for
for  ).
). 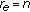 if and only if
if and only if  , that is,
, that is, 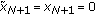 (Dirichlet conditions).
(Dirichlet conditions).
Hence, our construction leads to the maximal size (i.e.,
(i.e.,  ) of the constructed matrix for Dirichlet conditions
) of the constructed matrix for Dirichlet conditions  (more general for
(more general for  ) at the beginning and for natural boundary conditions (more general for
) at the beginning and for natural boundary conditions (more general for  ) at the end. The construction leads to the minimal size
) at the end. The construction leads to the minimal size for
for  (or for free
(or for free  ) at the beginning and for Dirichlet conditions
) at the beginning and for Dirichlet conditions  at the end.
at the end.
References
Kratz W: Banded matrices and difference equations. Linear Algebra and Its Applications 2001,337(1–3):1–20.
Wilkinson JH: The Algebraic Eigenvalue Problem. Clarendon Press, Oxford, UK; 1965:xviii+662.
Kratz W: Quadratic Functionals in Variational Analysis and Control Theory, Mathematical Topics. Volume 6. Akademie, Berlin, Germany; 1995:293.
Kratz W, Tentler M: Recursion formulae for the characteristic polynomial of symmetric banded matrices. Linear Algebra and Its Applications 2008,428(11–12):2482–2500. 10.1016/j.laa.2007.11.024
Tentler M: Rekursionsformeln zur Berechnung der charakteristischen Polynome von symmetrischen Bandmatrizen, Dissertation. Universität Ulm, Ulm, Germany; 2008.
Bohner M, Došlý O, Kratz W: Discrete Reid roundabout theorems. Dynamic Systems and Applications 1999,8(3–4):345–352.
Došlý O, Kratz W: Oscillation and spectral theory for symplectic difference systems with separated boundary conditions. to appear in Journal of Difference Equations and Applications
Bohner M, Došlý O, Kratz W: An oscillation theorem for discrete eigenvalue problems. The Rocky Mountain Journal of Mathematics 2003,33(4):1233–1260. 10.1216/rmjm/1181075460
Bohner M, Došlý O: Disconjugacy and transformations for symplectic systems. The Rocky Mountain Journal of Mathematics 1997,27(3):707–743. 10.1216/rmjm/1181071889
Bohner M, Došlý O, Kratz W: Inequalities and asymptotics for Riccati matrix difference operators. Journal of Mathematical Analysis and Applications 1998,221(1):262–286. 10.1006/jmaa.1997.5890
Ahlbrandt CD, Peterson AC: Discrete Hamiltonian Systems: Difference Equations, Continued Fractions, and Riccati Equation, Kluwer Texts in the Mathematical Sciences. Volume 16. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:xiv+374.
Došlý O, Kratz W: Oscillation theorems for symplectic difference systems. Journal of Difference Equations and Applications 2007,13(7):585–605. 10.1080/10236190701264776
Strang G: Linear Algebra and Its Applications. Academic Press, New York, NY, USA; 1976:xi+374.
Bohner M, Došlý O, Kratz W: Sturmian and spectral theory for discrete symplectic systems. Transactions of the American Mathematical Society 2009,361(6):3109–3123. 10.1090/S0002-9947-08-04692-8
Acknowledgment
This research is supported by Grant KR 1157/2-1 of DFG.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kratz, W. Banded Matrices and Discrete Sturm-Liouville Eigenvalue Problems. Adv Differ Equ 2009, 362627 (2010). https://doi.org/10.1155/2009/362627
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/362627
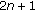 ,
,
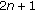 with
with 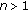 , and then even Dirichlet boundary conditions
, and then even Dirichlet boundary conditions  lead for the discrete problem to the boundary conditions
lead for the discrete problem to the boundary conditions  , which have to be complemented by additional "natural boundary conditions'' in the usual way. Therefore, such problems of second order with Dirichlet boundary conditions cannot be treated (at least for higher-order discretization) directly by the algorithm of [
, which have to be complemented by additional "natural boundary conditions'' in the usual way. Therefore, such problems of second order with Dirichlet boundary conditions cannot be treated (at least for higher-order discretization) directly by the algorithm of [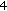 th- and
th- and 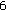 th-order Sturm-Liouville difference equations leads to bandwidths
th-order Sturm-Liouville difference equations leads to bandwidths 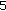 and
and  , and the numerical treatment of Dirichlet boundary conditions via [
, and the numerical treatment of Dirichlet boundary conditions via [ is equivalent with an algebraic eigenvalue problem for a banded, symmetric matrix under the assumptions (4.4) and (4.7). On the other hand, by [
is equivalent with an algebraic eigenvalue problem for a banded, symmetric matrix under the assumptions (4.4) and (4.7). On the other hand, by [ for all
for all  , then our eigenvalue problem
, then our eigenvalue problem  can be written as an eigenvalue problem for a corresponding Hamiltonian system or symplectic system [
can be written as an eigenvalue problem for a corresponding Hamiltonian system or symplectic system [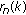 never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the difference equations by our construction leads in general to a problem where the leading coefficient may vanish for some
never vanishes, because it is the case in most applications. But the main point is that the incorporation of our general boundary conditions into the difference equations by our construction leads in general to a problem where the leading coefficient may vanish for some 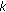 's at the beginning and the end. To be more precise, our construction may cause that matrix elements
's at the beginning and the end. To be more precise, our construction may cause that matrix elements  become zero at the beginning and at the end, so that its equivalent Sturm-Liouville problem with Dirichlet boundary conditions will not satisfy
become zero at the beginning and at the end, so that its equivalent Sturm-Liouville problem with Dirichlet boundary conditions will not satisfy for all
for all  anymore, because
anymore, because 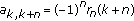 by (2.3). Hence, it cannot be written as an eigenvalue problem for a linear Hamiltonian difference system, so that the corresponding recursion formulae (based on the Hamiltonian or associated Riccati difference system [
by (2.3). Hence, it cannot be written as an eigenvalue problem for a linear Hamiltonian difference system, so that the corresponding recursion formulae (based on the Hamiltonian or associated Riccati difference system [ must be avoided, which is done by the division-free algorithms presented in [
must be avoided, which is done by the division-free algorithms presented in [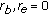 or
or  of our construction. It follows from (5.10) and (5.28) that
of our construction. It follows from (5.10) and (5.28) that  if and only if
if and only if 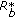 is invertible, that is,
is invertible, that is,  by (4.5) (this includes Dirichlet conditions
by (4.5) (this includes Dirichlet conditions for
for  ).
).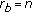 if and only if
if and only if  , that is,
, that is,  by (4.5) (so that
by (4.5) (so that  or
or 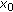 is free).
is free).  if and only if
if and only if 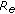 or
or  is invertible, that is,
is invertible, that is,  by (4.6) or
by (4.6) or  by (4.3) (this includes natural boundary conditions
by (4.3) (this includes natural boundary conditions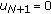 for
for  ).
). 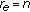 if and only if
if and only if  , that is,
, that is, 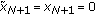 (Dirichlet conditions).
(Dirichlet conditions).