- Research Article
- Open access
- Published:
Existence of Periodic and Almost Periodic Solutions of Abstract Retarded Functional Difference Equations in Phase Spaces
Advances in Difference Equations volume 2009, Article number: 380568 (2009)
Abstract
The existence of periodic, almost periodic, and asymptotically almost periodic of periodic and almost periodic of abstract retarded functional difference equations in phase spaces is obtained by using stability properties of a bounded solution.
1. Introduction
In this paper, we study the existence of periodic, almost periodic, and asymptotic almost periodic solutions of the following functional difference equations with infinite delay:

assuming that this system possesses a bounded solution with some property of stability. In (1.1)  , and
, and  denotes an abstract phase space which we will define later.
denotes an abstract phase space which we will define later.
The abstract space was introduced by Hale and Kato [1] to study qualitative theory of functional differential equations with unbounded delay. There exists a lot of literature devoted to this subject; we refer the reader to Corduneanu and Lakshmikantham [2], Hino et al. [3]. The theory of abstract retarded functional difference equations in phase space has attracted the attention of several authors in recent years. We only mention here Murakami [4, 5], Elaydi et al. [6], Cuevas and Pinto [7, 8], Cuevas and Vidal [9], and Cuevas and Del Campo [10].
As usual, we denote by  ,
,  , and
, and  the set of all integers, the set of all nonnegative integers, and the set of all nonpositive integers, respectively. Let
the set of all integers, the set of all nonnegative integers, and the set of all nonpositive integers, respectively. Let  be the
be the  -dimensional complex Euclidean space with norm
-dimensional complex Euclidean space with norm  .
.  the set
the set  .
.
If  is a function, we define for
is a function, we define for , the function
, the function  by
by  ,
,  . Furthermore
. Furthermore  is the function given for
is the function given for  , with
, with  .
.
The abstract phase space  , which is a subfamily of all functions from
, which is a subfamily of all functions from  into
into  denoted by
denoted by  , is a normed space (with norm denoted by
, is a normed space (with norm denoted by  ) and satisfies the following axioms.
) and satisfies the following axioms.
-
(A)
There is a positive constant
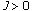 and nonnegative functions
and nonnegative functions
 and
and
 on
on
 with the property that
with the property that
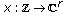 is a function, such that
is a function, such that
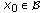 , then for all
, then for all
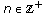 , the following conditions hold:
, the following conditions hold:
-
(i)
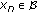 ,
, -
(ii)
 ,
, -
(iii)
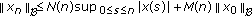 .
.
-
(i)
-
(B)
The space
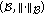 is a Banach space.
is a Banach space.
We need the following property on
 .
. -
(C)
The inclusion map
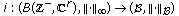 is continuous, that is, there is a constant
is continuous, that is, there is a constant
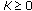 , such that
, such that
 , for all
, for all
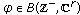 , where
, where
 represents the bounded functions from
represents the bounded functions from
 into
into
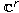 .
.
Axiom (C) says that any element of the Banach space of the bounded functions equipped with the supremum norm  is on
is on  .
.
Remark 1.1.
Using analogous ideas to the ones of [3], it is not difficult to prove that Axiom (C) is equivalente to the following.
-
(C')
If a uniformly bounded sequence
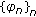 in
in 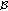 converges to a function
converges to a function  compactly on
compactly on  (i.e., converges on any compact discrete interval in
(i.e., converges on any compact discrete interval in 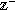 ) in the compact-open topology, then
) in the compact-open topology, then 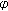 belong to
belong to 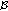 and
and 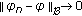 as
as 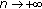 .
.
Remark 1.2.
We will denote by  (
( , and
, and  ) or simply by
) or simply by  , the solution of (1.1) passing through
, the solution of (1.1) passing through  , that is,
, that is,  , and the functional equation (1.1) is satisfied.
, and the functional equation (1.1) is satisfied.
During this paper we will assume that the sequences  and
and  are bounded. The paper is organized as follows. In Section 2 we see some important implications of the fading memory spaces. Section 3 is devoted to recall definitions and some important basic results about almost periodic sequences, asymptotically almost periodic sequences, and uniformly asymptotically almost periodic functions. In Section 4 we analyze separately the cases where
are bounded. The paper is organized as follows. In Section 2 we see some important implications of the fading memory spaces. Section 3 is devoted to recall definitions and some important basic results about almost periodic sequences, asymptotically almost periodic sequences, and uniformly asymptotically almost periodic functions. In Section 4 we analyze separately the cases where  is periodic and when it is almost periodic. Thus, in Section 4.1 assuming that the system (1.1) is periodic and the existence of a bounded solution (particular solution) which is uniformly stable and the phase space satisfies only the axioms (A)–(C), we prove the existence of an almost periodic solution and an asymptotically almost periodic solution. If additionally the particular solution is uniformly asymptotically stable, we prove the existence of a periodic solution. Similarly, in Section 4.2 considering that system (1.1) is almost periodic and the existence of a bounded solution and whenever the phase space satisfies the axioms (A)–(C), but here it is also necessary that
is periodic and when it is almost periodic. Thus, in Section 4.1 assuming that the system (1.1) is periodic and the existence of a bounded solution (particular solution) which is uniformly stable and the phase space satisfies only the axioms (A)–(C), we prove the existence of an almost periodic solution and an asymptotically almost periodic solution. If additionally the particular solution is uniformly asymptotically stable, we prove the existence of a periodic solution. Similarly, in Section 4.2 considering that system (1.1) is almost periodic and the existence of a bounded solution and whenever the phase space satisfies the axioms (A)–(C), but here it is also necessary that  verifies the fading memory property. If the particular solution is asymptotically almost periodic, then system (1.1) has an almost periodic solution. While, if the particular solution is uniformly asymptotically stable, we prove the existence of an asymptotically almost periodic solution.
verifies the fading memory property. If the particular solution is asymptotically almost periodic, then system (1.1) has an almost periodic solution. While, if the particular solution is uniformly asymptotically stable, we prove the existence of an asymptotically almost periodic solution.
In [11, 12] the problem of existence of almost periodic solutions for functional difference equations is considered in the first case for the discrete Volterra equation and in the second reference for the functional difference equations with finite delay; in both cases the authors assume the existence of a bounded solution with a property of stability that gives information about the existence of an almost periodic solution. In an analogous way in [13] the problem of the existence of almost periodic solutions for functional difference equations with infinite delay is considered. These results can be applied to several kinds of discrete equations. However, our approach differs from Hamaya's because, firstly, in our work we consider both cases, namely, when  is periodic and when it is almost periodic in the first variable. And secondly, we analyze very carefully the implications of the existence of a bounded solution of (1.1) with each property: uniformly stable, uniformly asymptotically stable, and globally uniformly stable.
is periodic and when it is almost periodic in the first variable. And secondly, we analyze very carefully the implications of the existence of a bounded solution of (1.1) with each property: uniformly stable, uniformly asymptotically stable, and globally uniformly stable.
Furthermore, we cite the articles [14–16] which are devoted to study almost periodic solutions of difference equations, but a little is known about almost periodic solutions, and in particular, for periodic solutions of nonlinear functional difference equations in phase space via uniform stability, uniformly asymptotically stability, and globally uniformly stability properties of a bounded solution.
2. Fading Memory Spaces and Implications
Following the terminology given in [3], we introduce the family of operators on  ,
,  , as
, as

with  . They constitute a family of linear operators on
. They constitute a family of linear operators on  having the semigroup property
having the semigroup property  for
for  . Immediately, the following result holds from Axiom (A):
. Immediately, the following result holds from Axiom (A):

Now, given any function  such that
such that  , we have the following decomposition:
, we have the following decomposition:

where

Then, we have the following decomposition of  ,
,  for
for  , where
, where

and  for all
for all  . Note that
. Note that

Let

be a subset of  , and let
, and let  be the restriction of
be the restriction of  to
to  . Clearly, the family
. Clearly, the family  ,
,  , is also a strongly continuous semigroup of bounded linear operators on
, is also a strongly continuous semigroup of bounded linear operators on  . It is given explicitly by
. It is given explicitly by

for  .
.
Definition 2.1.
A phase space  that satisfies axioms (A)-(B) and (
that satisfies axioms (A)-(B) and ( ) or (
) or ( ) and such that the semigroup
) and such that the semigroup  is strongly stable is called a fading memory space.
is strongly stable is called a fading memory space.
Remark 2.2.
Remember that a strongly continuous semigroup is strongly stable if for all  ,
,  as
as  .
.
Thus, we have the following result.
Lemma 2.3.
Let  , with
, with  , where
, where  is a fading memory space. If
is a fading memory space. If  as
as  , then
, then  as
as  .
.
Proof.
Firstly, we note that as before,  , where
, where  , for
, for  and
and

Then, by definition  as
as  because
because  . On the other hand, by hypothesis,
. On the other hand, by hypothesis,  as
as  , so it follows from Axiom (C') that
, so it follows from Axiom (C') that  . Therefore, we conclude that
. Therefore, we conclude that  as
as  .
.
3. Notations and Preliminary Results
In this section, we review the definitions of (uniformly) almost periodic, asymptotically almost periodic sequence, which have been discussed by several authors and present some related properties.
For our purpose, we introduce the following definitions and results about almost periodic discrete processes which are given in [3, 17, 18] for the continuous case. For the discrete case we mention [11, 12].
Definition 3.1.
A sequence  is called an almost periodic sequence if the
is called an almost periodic sequence if the  -translation set of
-translation set of  ,
,

is a relatively dense set in  for all
for all  ; that is, for any given
; that is, for any given  , there exists an integer
, there exists an integer  such that each discrete interval of length
such that each discrete interval of length  contains
contains  such that
such that

 is called the
is called the  -translation number of
-translation number of  . We will denote by
. We will denote by  the set of all such sequences. We will write that
the set of all such sequences. We will write that is a.p. if
is a.p. if  .
.
Definition 3.2.
A sequence  is called an asymptotically almost periodic sequence if
is called an asymptotically almost periodic sequence if

where  is an almost periodic sequence, and
is an almost periodic sequence, and  as
as  . We will denote by
. We will denote by  the set of all such sequences. We will write that
the set of all such sequences. We will write that is a.a.p. if
is a.a.p. if  .
.
In general, we will consider  a Banach space.
a Banach space.
Definition 3.3.
A function or sequence  is said to be almost periodic (abbreviated a.p.) in
is said to be almost periodic (abbreviated a.p.) in  if for every
if for every  there is
there is  such that among
such that among  consecutive integers there is one; call it
consecutive integers there is one; call it  , such that
, such that

Denote by  all such sequences, and
all such sequences, and  is said to be an almost periodic (a.p.) in
is said to be an almost periodic (a.p.) in  .
.
Definition 3.4.
A sequence  , (or
, (or  ),
),  , equivalently, a function
, equivalently, a function  (or,
(or,  ) is called asymptotically almost periodic if
) is called asymptotically almost periodic if  , where
, where  and
and  (or,
(or,  ) satisfying
) satisfying  as
as  (or,
(or,  ). Denote by
). Denote by  (or
(or  all such sequences, and
all such sequences, and  is said to be an asymptotically almost periodic on
is said to be an asymptotically almost periodic on  (or on
(or on  ) (a.a.p.) in
) (a.a.p.) in  .
.
Remark 3.5.
Almost periodic sequences can be also defined for any sequence  (
( ) or
) or  by requiring that
by requiring that  consecutive integers are in
consecutive integers are in  .
.
Definition 3.6.
Let  .
.  is said to be almost periodic in
is said to be almost periodic in  uniformly for
uniformly for  , if for any
, if for any  and every compact
and every compact  , there exists a positive integer
, there exists a positive integer  such that any interval of length
such that any interval of length  (i.e., among
(i.e., among  consecutive integers) contains an integer (or equivalently, there is one); call it
consecutive integers) contains an integer (or equivalently, there is one); call it  , for which
, for which

 is called the
is called the  -translation number of
-translation number of  . We will denote by
. We will denote by  the set of all such sequences. In brief we will write that
the set of all such sequences. In brief we will write that  is u.a.p. if
is u.a.p. if  .
.
Definition 3.7.
The hull of  , denoted by
, denoted by  , is defined by
, is defined by

for some sequence  , where
, where  is any compact set in
is any compact set in  .
.
For our purpose, we introduce the following definitions and results about almost periodic discrete processes which are given in [3, 17, 18] for the continuous case. For the discrete case we mention [11, 12]. With the objective to make this manuscript self contained we decided to include the majority of the proofs.
Lemma 3.8.
-
(a)
If
 is an a.p. sequence, then there exists an almost periodic function
is an a.p. sequence, then there exists an almost periodic function 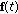 such that
such that 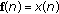 for
for 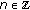 .
. -
(b)
If
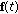 is an a.p. function, then
is an a.p. function, then  is an a.p. sequence.
is an a.p. sequence.
Lemma 3.9. (a) If  is an a.p. sequence, then
is an a.p. sequence, then  is bounded.
is bounded.
(b) is an a.p. sequence if and only if for any sequence
is an a.p. sequence if and only if for any sequence  there exists a subsequence
there exists a subsequence  such that
such that  converges uniformly on
converges uniformly on  as
as  . Furthermore, the limits sequence is also an almost periodic sequence.
. Furthermore, the limits sequence is also an almost periodic sequence.
(c)
 is an a.p. sequence if and only if for any sequence of integers
is an a.p. sequence if and only if for any sequence of integers  ,
,  there exist subsequences
there exist subsequences  ,
,  such that
such that

where  for
for  .
.
(d) ,
,  (or,
(or,  ) is an a.a.p. sequence if and only if for any sequence
) is an a.a.p. sequence if and only if for any sequence  (or,
(or,  ) such that
) such that  and
and  as
as  (or,
(or,  as
as  ), there exists a subsequence
), there exists a subsequence  such that
such that  converges uniformly on
converges uniformly on  (or
(or  ) as
) as  .
.
Lemma 3.10.
Let  be an a.a.p. periodic sequence. Then its decomposition,
be an a.a.p. periodic sequence. Then its decomposition,

where  is an a.p. sequence while
is an a.p. sequence while  as
as  , is unique.
, is unique.
Lemma 3.11.
Let  be almost periodic in
be almost periodic in  uniformly for
uniformly for  and continuous in
and continuous in  . Then
. Then  is bounded and uniformly continuous on
is bounded and uniformly continuous on  for any compact set
for any compact set  in
in  .
.
Lemma 3.12.
Let  be the same as in the previous lemma. Then, for any sequence
be the same as in the previous lemma. Then, for any sequence  , there exist a subsequence
, there exist a subsequence  of
of  and a function
and a function  continuous in
continuous in  such that
such that  uniformly on
uniformly on  as
as  , where
, where  is any compact set in
is any compact set in  . Moreover,
. Moreover,  is also almost periodic in
is also almost periodic in  uniformly for
uniformly for  .
.
Lemma 3.13.
Let  be the same as in the previous lemma. Then, there exists a sequence
be the same as in the previous lemma. Then, there exists a sequence  ,
,  as
as  such that
such that  uniformly on
uniformly on  as
as  , where
, where  is any compact set in
is any compact set in  .
.
Lemma 3.14.
Let  be almost periodic in
be almost periodic in  uniformly for
uniformly for  and continuous in
and continuous in  , and let
, and let  be an almost periodic sequence in
be an almost periodic sequence in  such that
such that  for all
for all  , where
, where  is a compact set in
is a compact set in  . Then
. Then  is almost periodic in
is almost periodic in  .
.
Lemma 3.15.
Let  be almost periodic in
be almost periodic in  uniformly for
uniformly for  and continuous in
and continuous in  , and let
, and let  be an almost periodic sequence in
be an almost periodic sequence in  such that
such that  for all
for all  , where
, where  is a compact set in
is a compact set in  and
and  for
for  . Then
. Then  is almost periodic in
is almost periodic in  .
.
Remark 3.16.
If  is a.a.p., then the decomposition
is a.a.p., then the decomposition  , in the definition of an a.a.p. function, is unique (see [18]).
, in the definition of an a.a.p. function, is unique (see [18]).
4. Existence of Almost Periodic Solutions
From now on we will assume that the system (1.1) has a unique solution for a given initial condition on  and without loss of generality
and without loss of generality  , thus
, thus  .
.
We will make the following assumptions on (1.1).
-
(H1)
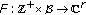 is continuous in the second variable for any fixed
is continuous in the second variable for any fixed 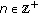 .
. -
(H2)
System (1.1) has a bounded solution
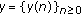 , passing through
, passing through 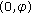 ,
, 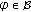 , that is,
, that is,  .
.
For this bounded solution  , there is an
, there is an  such that
such that  for all
for all  . So, we will have to assume that
. So, we will have to assume that  for all
for all  , and
, and  . Next, we will point out the definitions of stability for functional difference equations adapting it from the continuous case according to Hino et al. in [3].
. Next, we will point out the definitions of stability for functional difference equations adapting it from the continuous case according to Hino et al. in [3].
Definition 4.1.
A bounded solution  of (1.1) is said to be:
of (1.1) is said to be:
-
(i)
stable, if for any
 and any integer
and any integer 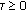 , there is
, there is  such that
such that 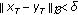 implies that
implies that  for all
for all  , where
, where  is any solution of (1.1);
is any solution of (1.1); -
(ii)
uniformly stable, abbreviated as "
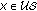 '', if for any
'', if for any  and any integer
and any integer  , there is
, there is  (
(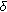 does not depend on
does not depend on  ) such that
) such that  implies that
implies that  for all
for all 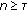 , where
, where 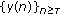 is any solution of (1.1);
is any solution of (1.1); -
(iii)
uniformly asymptotically stable, abbreviated as "
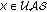 '', if it is uniformly stable and there is
'', if it is uniformly stable and there is 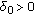 such that for any
such that for any 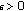 , there is a positive integer
, there is a positive integer  such that if
such that if 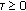 and
and 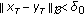 , then
, then  for all
for all  , where
, where  is any solution of (1.1);
is any solution of (1.1); -
(iv)
globally uniformly asymptotically stable, abbreviated as "
 '', if it is uniformly stable and
'', if it is uniformly stable and  as
as 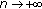 , whenever
, whenever 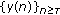 is any solution of (1.1).
is any solution of (1.1).
Remark 4.2.
It is easy to see that an equivalent definition for  , being
, being  , is the following:
, is the following:
-
(iii)
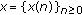 is
is 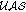 , if it is uniformly stable, and there exists
, if it is uniformly stable, and there exists 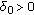 such that if
such that if  and
and  , then
, then 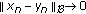 as
as  , where
, where  is any solution of (1.1).
is any solution of (1.1).
4.1. The Periodic Case
Here, we will assume what follows.
-
(H3)
The function
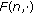 in (1.1) is periodic in
in (1.1) is periodic in 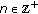 , that is, there exists a positive integer
, that is, there exists a positive integer 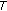 such that
such that 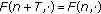 for all
for all  .
.
Moreover, we will assume what follows.
-
(
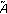 ) The sequences
) The sequences 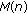 and
and  in Axiom (A)(iii) are bounded by
in Axiom (A)(iii) are bounded by 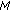 and
and 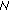 , respectively and
, respectively and 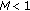 .
.
Lemma 4.3.
Suppose that condition (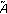 ) holds. If
) holds. If  is a bounded solution of (1.1) such that
is a bounded solution of (1.1) such that  , then
, then  is also bounded in
is also bounded in  .
.
Proof.
Let us say that  for all
for all  . Then by Axiom (A)(iii) and hypothesis (
. Then by Axiom (A)(iii) and hypothesis ( ) we have
) we have

Lemma 4.4.
Suppose that condition ( ) holds. Let
) holds. Let  be a sequence in
be a sequence in  such that
such that  for all
for all  . Assume that
. Assume that  as
as  for every
for every  and
and  , then
, then  in
in  as
as  for each
for each  . In particular, if
. In particular, if  as
as  uniformly in
uniformly in  , then
, then  in
in  as
as  uniformly in
uniformly in  .
.
Proof.
By Axiom (A)(iii) and hypotheses we have that

In the particular case  we obtain
we obtain

and so  as
as  . On the other hand, since
. On the other hand, since  is fixed, it follows that
is fixed, it follows that

for each  . Therefore, we have concluded the proof.
. Therefore, we have concluded the proof.
Theorem 4.5.
Suppose that condition ( ) and (H1)–(H3) hold. If the bounded solution
) and (H1)–(H3) hold. If the bounded solution  of (1.1) is
of (1.1) is  , then
, then  is an a.a.p. sequence in
is an a.a.p. sequence in  , equivalently, (1.1) has an a.a.p. solution.
, equivalently, (1.1) has an a.a.p. solution.
Proof.
By Lemma 4.3 there exists  such that
such that  for all
for all  , and a bounded (or compact) set
, and a bounded (or compact) set  such that
such that  for all
for all  . Let
. Let  be any integer sequence such that
be any integer sequence such that  and
and  as
as  . For each
. For each  , there exists a nonnegative integer
, there exists a nonnegative integer  such that
such that  . Set
. Set  . Then
. Then  for all
for all  . Since
. Since  is a bounded set, we can assume that, taking a subsequence if necessary,
is a bounded set, we can assume that, taking a subsequence if necessary,  for all
for all  , where
, where  . Now, set
. Now, set  . Thus,
. Thus,

which implies that  is a solution of the system,
is a solution of the system,

through  . It is clear that if
. It is clear that if  is
is  , then
, then  is also
is also  with the same pair
with the same pair  as the one for
as the one for  .
.
Since  is bounded for all
is bounded for all  and
and  , we can use the diagonal method to get a subsequence
, we can use the diagonal method to get a subsequence  of
of  such that
such that  converges for each
converges for each  as
as  . Thus, we can assume that the sequence
. Thus, we can assume that the sequence  converges for each
converges for each  as
as  . Since
. Since  , by Lemma 4.4 it follows that
, by Lemma 4.4 it follows that  is also convergent for each
is also convergent for each  . In particular, for any
. In particular, for any  there exists a positive integer
there exists a positive integer  such that if
such that if  (
( is the constant given in Axiom A(ii), then
is the constant given in Axiom A(ii), then

where  is the number given by the uniform stability of
is the number given by the uniform stability of  . Since
. Since  , it follows from Definition 4.1 and (4.7) that
, it follows from Definition 4.1 and (4.7) that

and by Axiom A(ii) it follows that

This implies that for any positive integer sequence  ,
,  as
as  , there is a subsequence
, there is a subsequence  of
of  for which
for which  converges uniformly on
converges uniformly on  as
as  . Thus, the conclusion of the theorem follows from Lemma 3.9(d).
. Thus, the conclusion of the theorem follows from Lemma 3.9(d).
Before proving our following result we remark that if  is a.a.p. then there are unique sequences
is a.a.p. then there are unique sequences  such that
such that  , with
, with  a.p. and
a.p. and  as
as  as
as  . By Lemma 3.9(a) it follows that
. By Lemma 3.9(a) it follows that  is bounded and thus
is bounded and thus  . Hence, by Axiom (C) we must have that
. Hence, by Axiom (C) we must have that  for all
for all  . In particular,
. In particular,  for all
for all  .
.
Theorem 4.6.
Suppose that  and (H1)–(H3) hold and the bounded solution
and (H1)–(H3) hold and the bounded solution  of (1.1) is
of (1.1) is  , then system (1.1) has an a.p. solution, which is also
, then system (1.1) has an a.p. solution, which is also  .
.
Proof.
It follows from Theorem 4.5 that  is an a.a.p. Set
is an a.a.p. Set  (
( ), where
), where  is a.p. sequence and
is a.p. sequence and  as
as  . For the positive integer sequence
. For the positive integer sequence  , by Lemma 3.9(b)–(d) and arguments of the previous theorem, we can choice a subsequence
, by Lemma 3.9(b)–(d) and arguments of the previous theorem, we can choice a subsequence  of
of  such that
such that  converges uniformly in
converges uniformly in  and
and  uniformly on
uniformly on  as
as  and
and  is also a.p. Then,
is also a.p. Then,  uniformly in
uniformly in  , and thus by Lemma 4.4
, and thus by Lemma 4.4 uniformly in
uniformly in  on
on  as
as  and
and  . Since
. Since

as  , we have
, we have  for
for  , that is, the system (1.1) has an almost periodic solution, and so we have proved the first statement of the theorem.
, that is, the system (1.1) has an almost periodic solution, and so we have proved the first statement of the theorem.
In order to prove the second affirmation, notice that  since
since  . For any
. For any  , let
, let  be a solution of (1.1) such that
be a solution of (1.1) such that  and
and  . Again, by Lemma 4.4
. Again, by Lemma 4.4 as
as  for each
for each  , so there is a positive integer
, so there is a positive integer  such that if
such that if  , then
, then

Thus, for  , we have
, we have

Then,

Therefore, there is  such that if
such that if  , then
, then

and hence,  for all
for all  , where
, where  is a pair for the uniform stability of
is a pair for the uniform stability of  . This shows that if
. This shows that if  , then
, then

for all  , which implies that
, which implies that  for all
for all  if
if  because
because  is arbitrary. This proves that
is arbitrary. This proves that  is
is  .
.
In the case when we have an asymptotically stable solution of (1.1) we obtain the following result.
Theorem 4.7.
Suppose that  and (H1)–(H3) hold and the bounded solution
and (H1)–(H3) hold and the bounded solution  of (1.1) is
of (1.1) is  , then the system (1.1) has a periodic solution of period
, then the system (1.1) has a periodic solution of period  for some positive integer
for some positive integer  , which is also
, which is also  .
.
Proof.
Set  ,
,  . By the proof of Theorem 4.5, there is a subsequence
. By the proof of Theorem 4.5, there is a subsequence  which converges to a solution
which converges to a solution  of (4.6) for each
of (4.6) for each  and hence by Lemma 4.4,
and hence by Lemma 4.4,  as
as  . Thus, there is a positive integer
. Thus, there is a positive integer  such that
such that  (
( ), where
), where  is obtained from the uniformly asymptotic stability of
is obtained from the uniformly asymptotic stability of  . Let
. Let  , and notice that
, and notice that  is a solution of (1.1). Since
is a solution of (1.1). Since  for
for  , that is,
, that is,  , we have
, we have

and hence,

because  is
is  (see also Remark 4.2). On the other hand,
(see also Remark 4.2). On the other hand,  is a.a.p. by Theorem 4.5, then
is a.a.p. by Theorem 4.5, then

where  is a.p. and
is a.p. and  as
as  . It follows from (4.17) and (4.18) that
. It follows from (4.17) and (4.18) that

which implies that  for all
for all  because
because  is a.p.
is a.p.
For the integer sequence  ,
,  , we have
, we have  . Then
. Then  uniformly for all
uniformly for all  as
as  , and again by Lemma 4.4,
, and again by Lemma 4.4,  uniformly in
uniformly in  as
as  . Since
. Since  , we have
, we have  for
for  , which implies that (1.1) has a periodic solution
, which implies that (1.1) has a periodic solution  of period
of period  .
.
Now, we will proceed to prove that  by the use of definition
by the use of definition  in Remark 4.2. Notice that since
in Remark 4.2. Notice that since  then
then  is a
is a  solution of (1.1) with the same
solution of (1.1) with the same  as the one for
as the one for  . Let
. Let  be any solution of (1.1) such that
be any solution of (1.1) such that  . Set
. Set  . Again, for sufficient large
. Again, for sufficient large  , we have the similar relations (4.12) and (4.14) with
, we have the similar relations (4.12) and (4.14) with  and
and  . Thus,
. Thus,

as  if
if  , because
, because  ,
,  , and
, and  satisfy (1.1). This completes the proof.
satisfy (1.1). This completes the proof.
Finally, if the particular solution is  , we will prove that system (1.1) has a periodic solution.
, we will prove that system (1.1) has a periodic solution.
Theorem 4.8.
Suppose that  and (H1)–(H3) hold and that the bounded solution
and (H1)–(H3) hold and that the bounded solution  of (1.1) is
of (1.1) is  , then the system (1.1) has a periodic solution of period
, then the system (1.1) has a periodic solution of period  .
.
Proof.
By Theorem 4.5,  is a.a.p. Then
is a.a.p. Then 
 ), where
), where  (
( ) is an a.p. sequence and
) is an a.p. sequence and  as
as  . Notice that
. Notice that  is also a solution of (1.1) satisfying
is also a solution of (1.1) satisfying  . Since
. Since  is
is  , we have that
, we have that  as
as  , which implies that
, which implies that  for all
for all  . Using same technique as in the proof of Theorem 4.7, we can show that
. Using same technique as in the proof of Theorem 4.7, we can show that  is a
is a  -periodic solution of (1.1).
-periodic solution of (1.1).
4.2. The Almost Periodic Case
Here, we will assume that
-
(H4)
the function
 in (1.1) is almost periodic in
in (1.1) is almost periodic in 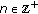 uniformly in the second variable.
uniformly in the second variable.
By  we denote the uniform closure of
we denote the uniform closure of  , that is,
, that is,  . Note that
. Note that  by Lemma 3.12 and
by Lemma 3.12 and  by Lemma 3.13.
by Lemma 3.13.
Lemma 4.9.
Suppose that Axiom (C) is true, and that  is an a.p. sequence with
is an a.p. sequence with  , then
, then  is a.p.
is a.p.
Proof.
We know that, given  , there exists an integer
, there exists an integer  such that each discrete interval of length
such that each discrete interval of length  contains a
contains a  such that
such that

By Axiom (C) we have

Lemma 4.10.
Suppose that  is a fading memory space and
is a fading memory space and  is a.a.p. with
is a.a.p. with  , then
, then  is a.a.p.
is a.a.p.
Proof.
Since  is a.a.p. there are unique sequences
is a.a.p. there are unique sequences  and
and  such that
such that  is a.p. and
is a.p. and  as
as  . Then by Lemma 4.9 it follows that
. Then by Lemma 4.9 it follows that  is a.p., and by Lemma 2.3 it follows that
is a.p., and by Lemma 2.3 it follows that  as
as  . Therefore,
. Therefore,  is a.a.p.
is a.a.p.
Theorem 4.11.
Suppose that conditions  , (H1)-(H2), and (H4) hold and that
, (H1)-(H2), and (H4) hold and that  is a fading memory space. If the bounded solution
is a fading memory space. If the bounded solution  of (1.1) is an a.a.p. sequence, then the system (1.1) has an a.p. solution.
of (1.1) is an a.a.p. sequence, then the system (1.1) has an a.p. solution.
Proof.
Since the solution  is a.a.p., it follows from Lemma 3.10 that
is a.a.p., it follows from Lemma 3.10 that  has a unique decomposition
has a unique decomposition  , where
, where  is a.p. and
is a.p. and  as
as  . Notice that
. Notice that  is bounded. By Lemma 4.3 there is a compact set
is bounded. By Lemma 4.3 there is a compact set  in
in  such that
such that  for all
for all  . By Lemma 3.13, there is an integer sequence
. By Lemma 3.13, there is an integer sequence  ,
,  , such that
, such that  as
as  and
and  uniformly on
uniformly on  as
as  . Taking a subsequence if necessary, we can also assume that
. Taking a subsequence if necessary, we can also assume that  uniformly on
uniformly on  , and by Lemma 3.9(b) we have that
, and by Lemma 3.9(b) we have that  is also an a.p. sequence. For any
is also an a.p. sequence. For any  , there is a positive integer
, there is a positive integer  such that if
such that if  , then
, then  . In this case, we see that
. In this case, we see that  uniformly for all
uniformly for all  as
as  , and hence by Lemma 4.4
, and hence by Lemma 4.4 in
in  in
in  as
as  . Since
. Since

and from the previous considerations the first term of the right-hand side of (4.23) tends to zero as  and since
and since  as
as  , we have that
, we have that  for all
for all  , which implies that (1.1) has an a.p. solution
, which implies that (1.1) has an a.p. solution  passing through
passing through  , where
, where  for
for  .
.
We are now in a position to prove the following result.
Theorem 4.12.
Suppose that the assumptions  , (H1), (H2), and (H4) hold, and that
, (H1), (H2), and (H4) hold, and that  is a fading memory space. If the bounded solution
is a fading memory space. If the bounded solution  of (1.1) is
of (1.1) is  , then
, then  is a.a.p. Consequently, (1.1) has an a.p. solution which is
is a.a.p. Consequently, (1.1) has an a.p. solution which is  .
.
Proof.
Let the bounded solution  of (1.1) be
of (1.1) be  with the triple
with the triple  . Let
. Let  be any positive integer such that
be any positive integer such that  as
as  . Set
. Set  . As previously
. As previously  is a solution of
is a solution of

and  is
is  with the same triple
with the same triple  . By Lemma A.2, for the set
. By Lemma A.2, for the set  and any
and any  there exists
there exists  such that
such that  and
and  for some
for some  implies that
implies that  for all
for all  , where
, where  is a bounded solution of
is a bounded solution of

passing through  and
and  for
for  . Since
. Since  is uniformly bounded for all
is uniformly bounded for all  and
and  , taking a subsequence if necessary, we can assume that
, taking a subsequence if necessary, we can assume that  is convergent for each
is convergent for each  and
and  uniformly on
uniformly on  , for some a.p. function
, for some a.p. function  . In this case, by Lemma 4.4 there is a positive integer
. In this case, by Lemma 4.4 there is a positive integer  such that if
such that if  , then
, then

On the other hand,  for
for  is a solution of (4.25) with
is a solution of (4.25) with  , that is,
, that is,

where  is defined by the relation
is defined by the relation

To apply Lemma A.2 to (4.24) and its associated equation (4.27), we will point out some properties of the sequence  . Since
. Since  uniformly on
uniformly on  , for the above
, for the above  , there is a positive integer
, there is a positive integer  such that if
such that if  , then
, then

which implies that  for all
for all  . Applying Lemma A.2 to (4.24) and its associated equation (4.27) with the above arguments and condition (4.26), we conclude that for any positive integer sequence
. Applying Lemma A.2 to (4.24) and its associated equation (4.27) with the above arguments and condition (4.26), we conclude that for any positive integer sequence  ,
,  as
as  , and
, and  , there is a positive integer
, there is a positive integer  such that
such that

and hence by Axiom A(ii)  for all
for all  if
if  . This implies that the bounded solution
. This implies that the bounded solution  of (1.1) is a.a.p. by Lemma 3.9(d). Furthermore, (1.1) has an a.p. solution, which is
of (1.1) is a.a.p. by Lemma 3.9(d). Furthermore, (1.1) has an a.p. solution, which is  by Theorem 4.11. This ends the proof.
by Theorem 4.11. This ends the proof.
Appendix
The proof of the following lemmas used ideas developed by Hino et al. in [3] for the functional differential equations with infinite delay and by Song [12] for functional difference equations with finite delay.Lemma A.1. Suppose that  , (H1), (H2), and (H4) hold and that
, (H1), (H2), and (H4) hold and that  is a fading memory space. Let
is a fading memory space. Let  be the bounded solution of (1.1). Let
be the bounded solution of (1.1). Let  be a positive integer sequence such that
be a positive integer sequence such that  ,
,  , and
, and  uniformly on
uniformly on  as
as  , where
, where  is any compact subset in
is any compact subset in  and
and  . If the bounded solution
. If the bounded solution  is
is  , then the solution
, then the solution  of
of

through  , is
, is  . In addition, if
. In addition, if  is
is  , then
, then  is also
is also  .Proof. Set
.Proof. Set  . It is easy to see that
. It is easy to see that  is a solution of
is a solution of

passing though  and
and  for all
for all  . Since
. Since  is
is  , then
, then is also
is also  with the same pair
with the same pair  as the one for
as the one for  . Taking a subsequence if necessary, we can assume that
. Taking a subsequence if necessary, we can assume that  converges to a vector
converges to a vector  for each
for each  as
as  . From (4.23) with
. From (4.23) with  , we can see that
, we can see that  is the unique solution of (A.1), satisfying
is the unique solution of (A.1), satisfying  because
because  .To show that the solution
.To show that the solution  of (A.1) is
of (A.1) is  , we need to prove that for any
, we need to prove that for any  and any integer
and any integer  , there exists
, there exists  such that
such that  implies that
implies that  for all
for all  , where
, where  is a solution of (A.1) with
is a solution of (A.1) with  .We know from Lemma 4.4 that
.We know from Lemma 4.4 that  as
as  for each
for each  ; thus, for any given
; thus, for any given  , if
, if  is sufficiently large; say
is sufficiently large; say  , we have
, we have

where  comes from the uniform stability of
comes from the uniform stability of  . Let
. Let  be such that
be such that

and let  be the solution of (1.1) such that
be the solution of (1.1) such that  . Then
. Then  is a solution of (A.2) with
is a solution of (A.2) with  . Since
. Since  is
is  and
and  for
for  , we have
, we have

It follows from (A.5) that

Then there exists a number  such that
such that  for all
for all  and
and  , which implies that there is a subsequence of
, which implies that there is a subsequence of  for each
for each  , denoted by
, denoted by  again, such that
again, such that  for each
for each  , and hence by Lemma 4.4
, and hence by Lemma 4.4 for all
for all  as
as  . Clearly,
. Clearly,  , and the set
, and the set  is compact set
is compact set  . Since
. Since  is almost periodic in
is almost periodic in  uniformly for
uniformly for  , we can assume that, taking a subsequence if necessary,
, we can assume that, taking a subsequence if necessary,  uniformly on
uniformly on  as
as  . Taking
. Taking  in
in  , we have
, we have  , namely,
, namely,  is the unique solution of (A.1), passing through
is the unique solution of (A.1), passing through  with
with  . On the other hand, for any integer
. On the other hand, for any integer  , there exists
, there exists  such that if
such that if  , then
, then

From (A.5) and (A.7), we obtain

Since  is arbitrary, we have
is arbitrary, we have  for all
for all  if
if  and
and  , which implies that the solution
, which implies that the solution  of (A.1) is
of (A.1) is  .Now, we consider the case where
.Now, we consider the case where  is
is  . Then the solution
. Then the solution  of (A.2) is also
of (A.2) is also  with the same pair
with the same pair  as the one for
as the one for  . Let
. Let  be the pair for uniform stability of
be the pair for uniform stability of  .For any given
.For any given  , if
, if  is sufficiently large; say
is sufficiently large; say  , we have
, we have

where  is the one for uniformly asymptotic stability of
is the one for uniformly asymptotic stability of  . Let
. Let  such that
such that  , and let
, and let  , for each fixed
, for each fixed  , be the solution of (1.1) such that
, be the solution of (1.1) such that  . Then
. Then  is a solution of (A.2) with
is a solution of (A.2) with  . Since
. Since  is
is  and
and  for each fixed
for each fixed  , we have
, we have

By the same argument as above, there is a subsequence of  , which we will continue calling
, which we will continue calling  , such that
, such that  converges to the solution
converges to the solution  of (A.1) through
of (A.1) through  and
and  uniformly on
uniformly on  as
as  , where
, where  is a compact set in
is a compact set in  with
with  for all
for all  and
and  . Then
. Then  is the unique solution of (A.1), passing through
is the unique solution of (A.1), passing through  with
with  . On the other hand, by Lemma 4.4 for any integer
. On the other hand, by Lemma 4.4 for any integer  there exists
there exists  such that if
such that if  , then
, then

and hence  for
for  . Since
. Since  is arbitrary, we have
is arbitrary, we have

if  and
and  ; thus,
; thus,  and the proof is complete.Now, we need to prove the following important lemma. Lemma A.2. Suppose that the assumptions
and the proof is complete.Now, we need to prove the following important lemma. Lemma A.2. Suppose that the assumptions  , (H1), (H2), and (H4) hold, that
, (H1), (H2), and (H4) hold, that  is a fading memory space, that the bounded solution
is a fading memory space, that the bounded solution  of (1.1) is
of (1.1) is  , and that for each
, and that for each  , the solution of (A.1) is unique for any given initial data. Let
, the solution of (A.1) is unique for any given initial data. Let  be a given compact set in
be a given compact set in  . Then for any
. Then for any  , there exists
, there exists  such that if
such that if  ,
,  , and
, and  is a sequence with
is a sequence with  for
for  , one has
, one has  for all
for all  , where
, where  is any bounded solution of the system
is any bounded solution of the system

passing through  and such that
and such that  for all
for all  .Proof. Suppose that the bounded solution
.Proof. Suppose that the bounded solution  of (1.1) is
of (1.1) is  with the triple
with the triple  . The proof will be by contradiction, we assume that Lemma A.2 is not true. Then for some compact set
. The proof will be by contradiction, we assume that Lemma A.2 is not true. Then for some compact set  , there exist
, there exist  ,
,  , sequences
, sequences  ,
,  , mapping sequences
, mapping sequences  ,
,  , and
, and

for sufficiently large  , where
, where  is a solution of
is a solution of

passing through  such that
such that  for all
for all  and
and  . Since
. Since  is a bounded subset of
is a bounded subset of  , it follows that
, it follows that  and
and  are uniformly bounded for all
are uniformly bounded for all  and
and  . We first consider the case where
. We first consider the case where  contains an unbounded subsequence. Set
contains an unbounded subsequence. Set  . Taking a subsequence if necessary, we may assume from Lemmas 3.12 and 3.9(b) that there is
. Taking a subsequence if necessary, we may assume from Lemmas 3.12 and 3.9(b) that there is  such that
such that  uniformly on
uniformly on  ,
,  , and
, and  for
for  as
as  , where
, where  are some bounded functions. Since
are some bounded functions. Since

passing to the limit as  , by the similar arguments in the proof of Theorem 4.11, we conclude that
, by the similar arguments in the proof of Theorem 4.11, we conclude that  is the solution of the following equation:
is the solution of the following equation:

Similarly,  is also a solution of (A.17). By Lemma 4.4
is also a solution of (A.17). By Lemma 4.4 and
and  in
in  as
as  ; it follows from (A.14) that
; it follows from (A.14) that  . Notice that
. Notice that  is a solution of (A.17), passing through
is a solution of (A.17), passing through  , and is
, and is  by Lemma A.1. We have
by Lemma A.1. We have  . On the other hand, since
. On the other hand, since

as  for each
for each  , it follows from (A.14) that
, it follows from (A.14) that

This is a contradiction. Thus, the sequence  must be bounded. Taking a subsequence if necessary, we can assume that
must be bounded. Taking a subsequence if necessary, we can assume that  . Moreover, we may assume that
. Moreover, we may assume that  and
and  for each
for each  , and
, and  uniformly on
uniformly on  , for some functions
, for some functions  ,
,  on
on  , and
, and  . Since
. Since  and
and  in
in  as
as  , we have
, we have  by (A.14), and hence
by (A.14), and hence  , that is,
, that is,  for all
for all  . Moreover,
. Moreover,  and
and  satisfy the same relation:
satisfy the same relation:

The uniqueness of the solutions for the initial value problems implies that  for
for  , and hence
, and hence  . On the other hand, and again from Lemma 4.4,
. On the other hand, and again from Lemma 4.4,  and
and  in
in  as
as  , then from (A.14) we have
, then from (A.14) we have

This is a contradiction, that proves Lemma A.2.
References
Hale JK, Kato J: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 1978,21(1):11-41.
Corduneanu C, Lakshmikantham V: Equations with unbounded delay: a survey. Nonlinear Analysis: Theory, Methods & Applications 1980,4(5):831-877. 10.1016/0362-546X(80)90001-2
Hino Y, Murakami S, Naito T: Functional-Differential Equations with Infinite Delay, Lecture Notes in Mathematics. Volume 1473. Springer, Berlin, Germany; 1991:x+317.
Murakami S: Representation of solutions of linear functional difference equations in phase space. Nonlinear Analysis: Theory, Methods & Applications 1997,30(2):1153-1164. 10.1016/S0362-546X(97)00296-4
Murakami S: Some spectral properties of the solution operator for linear Volterra difference systems. In New Developments in Difference Equations and Applications (Taipei, 1997). Gordon and Breach, Amsterdam, The Netherlands; 1999:301-311.
Elaydi S, Murakami S, Kamiyama E: Asymptotic equivalence for difference equations with infinite delay. Journal of Difference Equations and Applications 1999,5(1):1-23. 10.1080/10236199908808167
Cuevas C, Pinto M: Asymptotic behavior in Volterra difference systems with unbounded delay. Journal of Computational and Applied Mathematics 2000,113(1-2):217-225. 10.1016/S0377-0427(99)00257-5
Cuevas C, Pinto M: Convergent solutions of linear functional difference equations in phase space. Journal of Mathematical Analysis and Applications 2003,277(1):324-341. 10.1016/S0022-247X(02)00570-X
Cuevas C, Vidal C: Discrete dichotomies and asymptotic behavior for abstract retarded functional difference equations in phase space. Journal of Difference Equations and Applications 2002,8(7):603-640. 10.1080/10236190290032499
Cuevas C, Del Campo L: An asymptotic theory for retarded functional difference equations. Computers & Mathematics with Applications 2005,49(5-6):841-855. 10.1016/j.camwa.2004.06.032
Song Y, Tian H: Periodic and almost periodic solutions of nonlinear discrete Volterra equations with unbounded delay. Journal of Computational and Applied Mathematics 2007,205(2):859-870. 10.1016/j.cam.2005.12.042
Song Y: Periodic and almost periodic solutions of functional difference equations with finite delay. Advances in Difference Equations 2007, 2007:-15.
Hamaya Y: Existence of an almost periodic solution in a difference equation with infinite delay. Journal of Difference Equations and Applications 2003,9(2):227-237. 10.1080/1023619021000035836
Agarwal RP, O'Regan D, Wong PJY: Constant-sign periodic and almost periodic solutions of a system of difference equations. Computers & Mathematics with Applications 2005,50(10-12):1725-1754. 10.1016/j.camwa.2005.03.020
Ignatyev AO, Ignatyev OA: On the stability in periodic and almost periodic difference systems. Journal of Mathematical Analysis and Applications 2006,313(2):678-688. 10.1016/j.jmaa.2005.04.001
Zhang S, Liu P, Gopalsamy K: Almost periodic solutions of nonautonomous linear difference equations. Applicable Analysis 2002,81(2):281-301. 10.1080/0003681021000021961
Fink AM: Almost Periodic Differential Equations, Lecture Notes in Mathematics, vol. 377. Springer, Berlin, Germany; 1974:viii+336.
Zaidman S: Almost-Periodic Functions in Abstract Spaces, Research Notes in Mathematics. Volume 126. Pitman, Boston, Mass, USA; 1985:iii+133.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vidal, C. Existence of Periodic and Almost Periodic Solutions of Abstract Retarded Functional Difference Equations in Phase Spaces. Adv Differ Equ 2009, 380568 (2009). https://doi.org/10.1155/2009/380568
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/380568
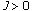 and nonnegative functions
and nonnegative functions
 and
and
 on
on
 with the property that
with the property that
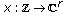 is a function, such that
is a function, such that
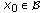 , then for all
, then for all
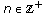 , the following conditions hold:
, the following conditions hold:
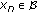 ,
, ,
,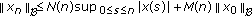 .
.
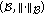 is a Banach space.
is a Banach space.
 .
.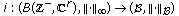 is continuous, that is, there is a constant
is continuous, that is, there is a constant
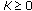 , such that
, such that
 , for all
, for all
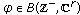 , where
, where
 represents the bounded functions from
represents the bounded functions from
 into
into
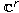 .
.
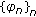 in
in 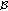 converges to a function
converges to a function  compactly on
compactly on  (i.e., converges on any compact discrete interval in
(i.e., converges on any compact discrete interval in 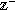 ) in the compact-open topology, then
) in the compact-open topology, then 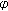 belong to
belong to 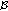 and
and 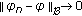 as
as 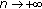 .
. is an a.p. sequence, then there exists an almost periodic function
is an a.p. sequence, then there exists an almost periodic function 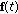 such that
such that 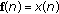 for
for 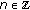 .
.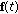 is an a.p. function, then
is an a.p. function, then  is an a.p. sequence.
is an a.p. sequence.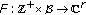 is continuous in the second variable for any fixed
is continuous in the second variable for any fixed 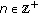 .
.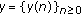 , passing through
, passing through 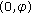 ,
, 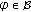 , that is,
, that is,  .
. and any integer
and any integer 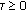 , there is
, there is  such that
such that 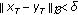 implies that
implies that  for all
for all  , where
, where  is any solution of (1.1);
is any solution of (1.1);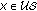 '', if for any
'', if for any  and any integer
and any integer  , there is
, there is  (
(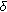 does not depend on
does not depend on  ) such that
) such that  implies that
implies that  for all
for all 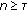 , where
, where 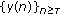 is any solution of (1.1);
is any solution of (1.1);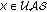 '', if it is uniformly stable and there is
'', if it is uniformly stable and there is 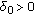 such that for any
such that for any 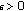 , there is a positive integer
, there is a positive integer  such that if
such that if 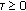 and
and 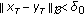 , then
, then  for all
for all  , where
, where  is any solution of (1.1);
is any solution of (1.1); '', if it is uniformly stable and
'', if it is uniformly stable and  as
as 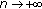 , whenever
, whenever 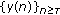 is any solution of (1.1).
is any solution of (1.1).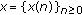 is
is 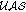 , if it is uniformly stable, and there exists
, if it is uniformly stable, and there exists 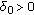 such that if
such that if  and
and  , then
, then 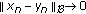 as
as  , where
, where  is any solution of (1.1).
is any solution of (1.1).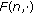 in (1.1) is periodic in
in (1.1) is periodic in 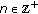 , that is, there exists a positive integer
, that is, there exists a positive integer 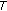 such that
such that 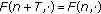 for all
for all  .
.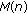 and
and  in Axiom (A)(iii) are bounded by
in Axiom (A)(iii) are bounded by 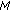 and
and 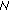 , respectively and
, respectively and 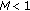 .
. in (1.1) is almost periodic in
in (1.1) is almost periodic in 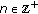 uniformly in the second variable.
uniformly in the second variable.