- Research Article
- Open access
- Published:
On a Conjecture for a Higher-Order Rational Difference Equation
Advances in Difference Equations volume 2009, Article number: 394635 (2009)
Abstract
This paper studies the global asymptotic stability for positive solutions to the higher order rational difference equation  , where
, where  is odd and
is odd and  . Our main result generalizes several others in the recent literature and confirms a conjecture by Berenhaut et al., 2007.
. Our main result generalizes several others in the recent literature and confirms a conjecture by Berenhaut et al., 2007.
1. Introduction
In 2007, Berenhaut et al. [1] proved that every solution of the following rational difference equation

converges to its unique equilibrium  , where
, where  and
and  . Based on this fact, they put forward the following two conjectures.
. Based on this fact, they put forward the following two conjectures.
Conjecture.
Suppose that  and that
and that  atisfies
atisfies

with  Then, the sequence
Then, the sequence  converges to the unique equilibrium 1.
converges to the unique equilibrium 1.
Conjecture.
Suppose that  is odd and
is odd and  , and define
, and define  . If
. If  satisfies
satisfies

with  , where
, where

Then the sequence  converges to the unique equilibrium 1.
converges to the unique equilibrium 1.
Motivated by [2], Berenhaut et al. started with the investigation of the following difference equation  for
for  (see, [3, 4]). Among others, in [3] they used a transformation method, which has turned out to be very useful in studying (1.1) and (1.2) as well as in confirming Conjecture 1.1; see [5].
(see, [3, 4]). Among others, in [3] they used a transformation method, which has turned out to be very useful in studying (1.1) and (1.2) as well as in confirming Conjecture 1.1; see [5].
Some particular cases of (1.2) had been studied previously by Li in [6, 7], by using semicycle analysis similar to that in [8]. The problem concerning periodicity of semicycles of difference equations was solved in very general settings by Berg and Stević in [9], partially motivated also by [10].
In the meantime, it turned out that the method used in [11] by Çinar et al. can be used in confirming Conjecture 1.2 (see also [12]). More precisely [11, 12] use Corollary 3 from [13] in solving similar problems. For example, Çinar et al. has shown, in an elegant way, that the main result in [14] is a consequence of Corollary 3 in [13]. With some calculations it can be also shown that Conjecture 1.2 can be confirmed in this way (see [15]).
Some other related results can be found in [16–24].
In this paper, we will prove that Conjecture 1.2 is correct by using a new method. Obviously, our results generalize the corresponding works in [1, 5–7] and other literature.
2. Preliminaries and Notations
Observe that

Define function  as follows:
as follows:

Then we can rewrite (1.3) as

or

where  is an odd integer and
is an odd integer and  .
.
The following lemma can be obtained by simple calculations.
Lemma 2.1.
Let  be defined by (2.2). Then
be defined by (2.2). Then


Lemma 2.2.
Assume that  . If
. If  , then
, then

where

 .
.
Proof.
Since  is symmetric in
is symmetric in  , we can assume, without loss of generality, that
, we can assume, without loss of generality, that  . Then there are
. Then there are  possible cases:
possible cases:
-
(1)
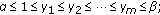
-
(2)

-
(3)
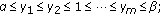
-
(4)
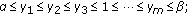

(m+1)
And, for the above cases  –(m+1), by the monotonicity of
–(m+1), by the monotonicity of  , in turn, we may get
, in turn, we may get
-
(1)
 ;
; -
(2)
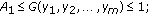
-
(3)

-
(4)
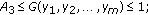

(m+1) .
.
From the above inequalities, it follows that (2.6) holds. The proof is complete.
Lemma 2.3.
Assume that  . Then
. Then


 .
.
Proof.
For  , it is easy to see that
, it is easy to see that

which yields

and so

It follows that (2.8) holds. Similarly, for  , it is easy to see that
, it is easy to see that

which yields

It follows that (2.9) holds. The proof is complete.
Lemma 2.4.
Let

where

 Assume that
Assume that  Then
Then

Proof.
By induction, we easily show that

It follows from Lemma 2.3 that

 Hence, by (2.15) and (2.18), we have
Hence, by (2.15) and (2.18), we have

Equation (2.20) implies that the limits  and
and  exist, and
exist, and

It follows from (2.16) that

 . Let
. Let  in (2.15), we have
in (2.15), we have

It follows that there exist  such that
such that

From (2.24), we have

Since

it follows from (2.25) and (2.18) that  . The proof is complete.
. The proof is complete.
3. Proof of Conjecture 1.2
Theorem 3.1.
Suppose that  and that
and that

Then the solution  of (1.3) satisfies
of (1.3) satisfies

Theorem 3.1 is a direct corollary of Lemmas 2.2 and 2.3.
Proof.
Let  be a solution of (1.3) with
be a solution of (1.3) with  . We need to prove that
. We need to prove that

Choose  and
and  such that
such that

In view of Theorem 3.1, we have

Let  , and
, and  be defined as in Lemma 2.4. Then by (3.5) and Lemma 2.2, we have
be defined as in Lemma 2.4. Then by (3.5) and Lemma 2.2, we have

That is

By (3.7) and Lemma 2.2, we obtain

That is

Repeating the above procedure, in general, we can obtain

By Lemma 2.4, we have

which implies that (3.3) holds. The proof of Conjecture 1.2 is complete.
References
Berenhaut KS, Foley JD, Stević S:The global attractivity of the rational difference equation
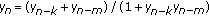 . Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022
. Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022Stević S:On the recursive sequence
 . Journal of Applied Mathematics & Computing 2005,18(1-2):229-234. 10.1007/BF02936567
. Journal of Applied Mathematics & Computing 2005,18(1-2):229-234. 10.1007/BF02936567Berenhaut KS, Foley JD, Stević S:The global attractivity of the rational difference equation
 . Proceedings of the American Mathematical Society 2007,135(4):1133-1140. 10.1090/S0002-9939-06-08580-7
. Proceedings of the American Mathematical Society 2007,135(4):1133-1140. 10.1090/S0002-9939-06-08580-7Berenhaut KS, Foley JD, Stević S:The global attractivity of the rational difference equation
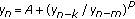 . Proceedings of the American Mathematical Society 2008,136(1):103-110. 10.1090/S0002-9939-07-08860-0
. Proceedings of the American Mathematical Society 2008,136(1):103-110. 10.1090/S0002-9939-07-08860-0Berenhaut KS, Stević S: The global attractivity of a higher order rational difference equation. Journal of Mathematical Analysis and Applications 2007,326(2):940-944. 10.1016/j.jmaa.2006.02.087
Li X: Qualitative properties for a fourth-order rational difference equation. Journal of Mathematical Analysis and Applications 2005,311(1):103-111. 10.1016/j.jmaa.2005.02.063
Li X: Global behavior for a fourth-order rational difference equation. Journal of Mathematical Analysis and Applications 2005,312(2):555-563. 10.1016/j.jmaa.2005.03.097
Amleh AM, Kruse N, Ladas G: On a class of difference equations with strong negative feedback. Journal of Difference Equations and Applications 1999,5(6):497-515. 10.1080/10236199908808204
Berg L, Stević S: Linear difference equations mod 2 with applications to nonlinear difference equations. Journal of Difference Equations and Applications 2008,14(7):693-704. 10.1080/10236190701754891
Berg L, Stević S: Periodicity of some classes of holomorphic difference equations. Journal of Difference Equations and Applications 2006,12(8):827-835. 10.1080/10236190600761575
Çinar C, Stević S, Yalçinkaya I: A note on global asymptotic stability of a family of rational equations. Rostocker Mathematisches Kolloquium 2005, 59:41-49.
Stević S: Global stability and asymptotics of some classes of rational difference equations. Journal of Mathematical Analysis and Applications 2006,316(1):60-68. 10.1016/j.jmaa.2005.04.077
Kruse N, Nesemann T: Global asymptotic stability in some discrete dynamical systems. Journal of Mathematical Analysis and Applications 1999,235(1):151-158. 10.1006/jmaa.1999.6384
Li X, Zhu D: Global asymptotic stability in a rational equation. Journal of Difference Equations and Applications 2003,9(9):833-839. 10.1080/1023619031000071303
Aloqeily M: Global stability of a rational symmetric difference equation. preprint, 2008
Gutnik L, Stević S: On the behaviour of the solutions of a second-order difference equation. Discrete Dynamics in Nature and Society 2007, 2007:-14.
Ladas G: A problem from the Putnam Exam. Journal of Difference Equations and Applications 1998,4(5):497-499. 10.1080/10236199808808157
Putnam Exam The American Mathematical Monthly 1965, 734-736.
Stević S: Asymptotics of some classes of higher-order difference equations. Discrete Dynamics in Nature and Society 2007, 2007:-20.
Stević S: Existence of nontrivial solutions of a rational difference equation. Applied Mathematics Letters 2007,20(1):28-31. 10.1016/j.aml.2006.03.002
Stević S: Nontrivial solutions of a higher-order rational difference equation. Matematicheskie Zametki 2008,84(5):772-780.
Sun T, Xi H: Global asymptotic stability of a higher order rational difference equation. Journal of Mathematical Analysis and Applications 2007,330(1):462-466. 10.1016/j.jmaa.2006.07.096
Yang X, Sun F, Tang YY: A new part-metric-related inequality chain and an application. Discrete Dynamics in Nature and Society 2008, 2008:-7.
Yang X, Tang YY, Cao J: Global asymptotic stability of a family of difference equations. Computers & Mathematics with Applications 2008,56(10):2643-2649. 10.1016/j.camwa.2008.04.032
Acknowledgments
The authors are grateful to the referees for their careful reading of the manuscript and many valuable comments and suggestions that greatly improved the presentation of this work. This work is supported partly by NNSF of China (Grant: 10771215, 10771094), Project of Hunan Provincial Youth Key Teacher and Project of Hunan Provincial Education Department (Grant: 07C639).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liao, M., Tang, X. & Xu, C. On a Conjecture for a Higher-Order Rational Difference Equation. Adv Differ Equ 2009, 394635 (2009). https://doi.org/10.1155/2009/394635
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/394635
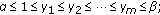

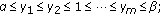
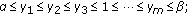
 ;
;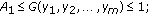

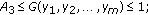
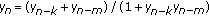 . Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022
. Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022 . Journal of Applied Mathematics & Computing 2005,18(1-2):229-234. 10.1007/BF02936567
. Journal of Applied Mathematics & Computing 2005,18(1-2):229-234. 10.1007/BF02936567 . Proceedings of the American Mathematical Society 2007,135(4):1133-1140. 10.1090/S0002-9939-06-08580-7
. Proceedings of the American Mathematical Society 2007,135(4):1133-1140. 10.1090/S0002-9939-06-08580-7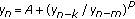 . Proceedings of the American Mathematical Society 2008,136(1):103-110. 10.1090/S0002-9939-07-08860-0
. Proceedings of the American Mathematical Society 2008,136(1):103-110. 10.1090/S0002-9939-07-08860-0