- Research Article
- Open access
- Published:
An Extension to Nonlinear Sum-Difference Inequality and Applications
Advances in Difference Equations volume 2009, Article number: 486895 (2009)
Abstract
We establish a general form of sum-difference inequality in two variables, which includes both more than two distinct nonlinear sums without an assumption of monotonicity and a nonconstant term outside the sums. We employ a technique of monotonization and use a property of stronger monotonicity to give an estimate for the unknown function. Our result enables us to solve those discrete inequalities considered in the work of W.-S. Cheung (2006). Furthermore, we apply our result to a boundary value problem of a partial difference equation for boundedness, uniqueness, and continuous dependence.
1. Introduction
Gronwall-Bellman inequality [1, 2] is a fundamental tool in the study of existence, uniqueness, boundedness, stability, invariant manifolds and other qualitative properties of solutions of differential equations and integral equation. There are a lot of papers investigating them such as [3–15]. Along with the development of the theory of integral inequalities and the theory of difference equations, more attentions are paid to some discrete versions of Bellman-Gronwall type inequalities (e.g., [16–18]). Starting from the basic form

discussed in [19], an interesting direction is to consider the inequality

a discrete version of Dafermos' inequality [20], where  are nonnegative constants and
are nonnegative constants and  are nonnegative functions defined on
are nonnegative functions defined on  and
and  , respectively. Pang and Agarwal [21] proved for (1.2) that
, respectively. Pang and Agarwal [21] proved for (1.2) that  for all
for all  . Another form of sum-difference inequality
. Another form of sum-difference inequality

was estimated by Pachpatte [22] as  , where
, where  . Recently, Pachpatte [23, 24] discussed the inequalities of two variables
. Recently, Pachpatte [23, 24] discussed the inequalities of two variables

where  is nondecreasing. In [25] another form of inequality of two variables
is nondecreasing. In [25] another form of inequality of two variables

was discussed. Later, this result was generalized in [26] to the inequality

where  ,
,  , and
, and  are all constants,
are all constants,  , and
, and  are both nonnegative real-valued functions defined on a lattice in
are both nonnegative real-valued functions defined on a lattice in  , and
, and  is a continuous nondecreasing function satisfying
is a continuous nondecreasing function satisfying  for all
for all  .
.
In this paper we establish a more general form of sum-difference inequality with positive integers  ,
,

where  . In (1.7) we replace the constant
. In (1.7) we replace the constant  , the functions
, the functions  ,
,  ,
,  ,
,  and
and  in (1.6) with a function
in (1.6) with a function  , more general functions
, more general functions  ,
,  and
and  , respectively. Moreover, we consider more than two nonlinear terms and do not require the monotonicity of every
, respectively. Moreover, we consider more than two nonlinear terms and do not require the monotonicity of every  . We employ a technique of monotonization to construct a sequence of functions which possesses stronger monotonicity than the previous one. Unlike the work in [26] for two sum terms, the maximal regions of validity for our estimate of the unknown function
. We employ a technique of monotonization to construct a sequence of functions which possesses stronger monotonicity than the previous one. Unlike the work in [26] for two sum terms, the maximal regions of validity for our estimate of the unknown function  are decided by boundaries of more than two planar regions. Thus we have to consider the inclusion of those regions and find common regions. We demonstrate that inequalities (1.6) and other inequalities considered in [26] can also be solved with our result. Furthermore, we apply our result to boundary value problems of a partial difference equation for boundedness, uniqueness, and continuous dependence.
are decided by boundaries of more than two planar regions. Thus we have to consider the inclusion of those regions and find common regions. We demonstrate that inequalities (1.6) and other inequalities considered in [26] can also be solved with our result. Furthermore, we apply our result to boundary value problems of a partial difference equation for boundedness, uniqueness, and continuous dependence.
2. Main Result
Throughout this paper, let  ,
,  , and
, and  ,
,  are given nonnegative integers. For any integers
are given nonnegative integers. For any integers  , let
, let  ,
,  , and
, and  . Define
. Define  , and let
, and let  denote the sublattice
denote the sublattice  in
in  for any
for any  .
.
For functions  , their first-order differences are defined by
, their first-order differences are defined by  and
and  . Obviously, the linear difference equation
. Obviously, the linear difference equation  with the initial condition
with the initial condition  has the solution
has the solution  . In the sequel, for convenience, we complementarily define that
. In the sequel, for convenience, we complementarily define that  .
.
We give the following basic assumptions for the inequality (1.7).
-
(H1)
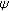 is a strictly increasing continuous function on
is a strictly increasing continuous function on 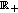 satisfying that
satisfying that  and
and 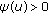 for all
for all 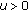 .
. -
(H2) All
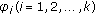 are continuous and positive functions on
are continuous and positive functions on  .
. -
(H3)
 on
on 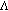 .
. -
(H4) All
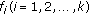 are nonnegative functions on
are nonnegative functions on 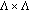 .
.
With given functions  , and
, and  , we technically consider a sequence of functions
, we technically consider a sequence of functions  , which can be calculated recursively by
, which can be calculated recursively by

For given constants  and variable
and variable  , we define
, we define

Obviously,  is strictly increasing in
is strictly increasing in  and therefore the inverses
and therefore the inverses  are well defined, continuous, and increasing. Let
are well defined, continuous, and increasing. Let

which is nondecreasing in  and
and  for each fixed
for each fixed  and
and  and satisfies
and satisfies  for all
for all  .
.
Theorem 2.1.
Suppose that  hold and
hold and  is a nonnegative function on
is a nonnegative function on  satisfying (1.7). Then, for
satisfying (1.7). Then, for  , a sublattice in
, a sublattice in  ,
,

where  is determined recursively by
is determined recursively by

and  is arbitrarily given on the boundary of the lattice
is arbitrarily given on the boundary of the lattice

Remark 2.2.
As explained in [3, Remark  ], since different choices of
], since different choices of  in
in 
 do not affect our results, we simply let
do not affect our results, we simply let  denote
denote  when there is no confusion. For positive constants
when there is no confusion. For positive constants  , let
, let  . Obviously,
. Obviously,  and
and  . It follows that
. It follows that

that is, we obtain the same expression in (2.4) if we replace  with
with  . Moreover, by replacing
. Moreover, by replacing  with
with  , the condition in the definition of
, the condition in the definition of  in Theorem 2.1 reads
in Theorem 2.1 reads

the left-hand side of which is equal to

and the right-hand side of which equals

The comparison between the both sides implies that (2.8) is equivalent to the condition given in the definition of  in Theorem 2.1 with
in Theorem 2.1 with  .
.
Remark 2.3.
If we choose  ,
,  ,
,  ,
,  with
with  ,
,  and
and  and restrict
and restrict  to be a constant
to be a constant  in (1.7), then we can apply Theorem 2.1 to inequality (1.6) discussed in [26].
in (1.7), then we can apply Theorem 2.1 to inequality (1.6) discussed in [26].
3. Proof of Theorem
First of all, we monotonize some given functions  ,
,  in the sums. Obviously, the sequence
in the sums. Obviously, the sequence  defined by
defined by  in (2.1) consists of nondecreasing nonnegative functions and satisfies
in (2.1) consists of nondecreasing nonnegative functions and satisfies  , for
, for  . Moreover,
. Moreover,

as defined in [27] for comparison of monotonicity of functions  , because every ratio
, because every ratio  is nondecreasing. By the definitions of functions
is nondecreasing. By the definitions of functions  , and
, and  , from (1.7) we get
, from (1.7) we get

Then, we discuss the case that  for all
for all  . Because
. Because  satisfies
satisfies

it is positive and nondecreasing on  . We consider the auxiliary inequality to (3.2), for all
. We consider the auxiliary inequality to (3.2), for all  ,
,

where  and
and  are chosen arbitrarily, and claim that, for
are chosen arbitrarily, and claim that, for  , a sublattice in
, a sublattice in  ,
,

where  is determined recursively by
is determined recursively by

 , and
, and  is arbitrarily chosen on the boundary of the lattice
is arbitrarily chosen on the boundary of the lattice

We note that  ,
,  can be chosen appropriately such that
can be chosen appropriately such that

In fact, from the fact of  being on the boundary of the lattice
being on the boundary of the lattice  , we see that
, we see that

Thus, it means that we can take  . Moreover,
. Moreover,  ,
,  .
.
In the following, we will use mathematical induction to prove (3.5).
For  , let
, let  . Then
. Then  is nonnegative and nondecreasing in each variable on
is nonnegative and nondecreasing in each variable on  . From (3.4) we observe that
. From (3.4) we observe that

Moreover, we note that  is nondecreasing and satisfies
is nondecreasing and satisfies  for
for  and that
and that  . From (3.10) we have
. From (3.10) we have

On the other hand, by the Mean Value Theorem for integral and by the monotonicity of  and
and  , for arbitrarily given
, for arbitrarily given  ,
,  there exists
there exists  in the open interval
in the open interval  such that
such that

It follows from (3.11) and (3.12) that

Substituting  with
with  and summing both sides of (3.13) from
and summing both sides of (3.13) from  to
to  , we get, for all
, we get, for all  ,
,

We note from the definition of  in (3.2) and the definition of
in (3.2) and the definition of  in Section 2 that
in Section 2 that  . By the monotonicity of
. By the monotonicity of  and (3.10) we obtain
and (3.10) we obtain

that is, (3.5) is true for  .
.
Next, we make the inductive assumption that (3.5) is true for  . Consider
. Consider

for all  . Let
. Let  which is nonnegative and nondecreasing in each variable on
which is nonnegative and nondecreasing in each variable on  . Then (3.16) is equivalent to
. Then (3.16) is equivalent to

Since  is nondecreasing and satisfies
is nondecreasing and satisfies  for
for  and
and  , from (3.17) we obtain, for all
, from (3.17) we obtain, for all  ,
,

where

On the other hand, by the Mean Value Theorem for integrals and by the monotonicity of  and
and  , for arbitrarily given
, for arbitrarily given  there exists
there exists  in the open interval
in the open interval  such that
such that

Therefore, it follows from (3.18) and (3.20) that

substituting  with
with  in (3.21) and summing both sides of (3.21) from
in (3.21) and summing both sides of (3.21) from  to
to  , we get, for all
, we get, for all  ,
,

where we note that  . For convenience, let
. For convenience, let

From (3.17) and (3.22) we can get

the same form as (3.4) for  , for all
, for all  , where we note that
, where we note that  for all
for all  . We are ready to use the inductive assumption for (3.24). In order to demonstrate the basic condition of monotonicity, let
. We are ready to use the inductive assumption for (3.24). In order to demonstrate the basic condition of monotonicity, let  obviously which is a continuous and nondecreasing function on
obviously which is a continuous and nondecreasing function on  . Thus each
. Thus each  is continuous and nondecreasing on
is continuous and nondecreasing on  and satisfies
and satisfies  for
for  . Moreover,
. Moreover,

which is also continuous nondecreasing on  and positive on
and positive on  . This implies that
. This implies that  , for
, for  . Therefore, the inductive assumption for (3.5) can be used to (3.24) and we obtain, for all
. Therefore, the inductive assumption for (3.5) can be used to (3.24) and we obtain, for all  ,
,

where  ,
,  is the inverse of
is the inverse of  (for
(for  ),
),  is determined recursively by
is determined recursively by

and  ,
,  are functions of
are functions of  such that
such that  lie on the boundary of the lattice
lie on the boundary of the lattice

where  denotes either
denotes either  if it converges or
if it converges or  . Note that
. Note that

Thus, from (3.17), (3.23), and (3.27), (3.26) can be equivalently written as

We further claim that the term  is the same as
is the same as  , defined in (3.6),
, defined in (3.6),  . For convenience, let
. For convenience, let  . Obviously, it is that
. Obviously, it is that  .
.
The remainder case is that  for some
for some  . Let
. Let

where  is an arbitrary small number. Obviously,
is an arbitrary small number. Obviously,  for all
for all  . Using the same arguments as above and replacing
. Using the same arguments as above and replacing  with
with  , we get
, we get

for all  .
.
Considering continuities of  and
and  for
for  as well as of
as well as of  in
in  and letting
and letting  , we obtain (2.4). This completes the proof.
, we obtain (2.4). This completes the proof.
We remark that  ,
,  lie on the boundary of the lattice
lie on the boundary of the lattice  . In particular, (2.4) is true for all
. In particular, (2.4) is true for all  when every
when every  (
( ) satisfies
) satisfies  . Therefore, we may take
. Therefore, we may take  ,
,  .
.
4. Applications to a Difference Equation
In this section we apply our result to the following boundary value problem (simply called BVP) for the partial difference equation:

where  is defined as in the beginning of Section 2,
is defined as in the beginning of Section 2,  is strictly increasing odd function satisfying
is strictly increasing odd function satisfying  for
for  ,
,  satisfies
satisfies

for given functions  and
and  (
( ) satisfying
) satisfying  for
for  , and functions
, and functions  and
and  satisfy that
satisfy that  . Obviously, (4.1) is a generalization of the BVP problem considered by [26, Section 3], and the theorems of [26] are not able to solve it. In the following we first apply our main result to the discussion of boundedness of (4.1).
. Obviously, (4.1) is a generalization of the BVP problem considered by [26, Section 3], and the theorems of [26] are not able to solve it. In the following we first apply our main result to the discussion of boundedness of (4.1).
Corollary 4.1.
All solutions  of BVP (4.1) have the following estimation for all
of BVP (4.1) have the following estimation for all 

where  are given as in Theorem 2.1 and
are given as in Theorem 2.1 and

Proof.
Clearly, the difference equation of BVP (4.1) is equivalent to

It follows, by (4.2), that

Let  . Since
. Since  , (4.6) is of the form (1.6). Applying our Theorem 2.1 to inequality (4.6), we obtain the estimate of
, (4.6) is of the form (1.6). Applying our Theorem 2.1 to inequality (4.6), we obtain the estimate of  as given in this corollary.
as given in this corollary.
Corollary 4.1 gives a condition of boundedness for solutions. Concretely, if

for all  , then every solution
, then every solution  of BVP (4.1) is bounded on
of BVP (4.1) is bounded on  .
.
Next, we discuss the uniqueness of solutions for BVP (4.1).
Corollary 4.2.
Suppose additionally that

for  and
and  , where
, where  as assumed in the beginning of Section 2 with natural numbers
as assumed in the beginning of Section 2 with natural numbers  and
and  are both nonnegative functions defined on the lattice
are both nonnegative functions defined on the lattice  ,
,  are both nondecreasing with the nondecreasing ratio
are both nondecreasing with the nondecreasing ratio  such that
such that  ,
,  for all
for all  and
and  for
for  and
and  is strictly increasing odd function satisfying
is strictly increasing odd function satisfying  for
for  . Then BVP (4.1) has at most one solution on
. Then BVP (4.1) has at most one solution on  .
.
Proof.
Assume that both  and
and  are solutions of BVP (4.1). From the equivalent form (4.5) of (4.1) we have
are solutions of BVP (4.1). From the equivalent form (4.5) of (4.1) we have

for all  , which is an inequality of the form (1.7), where
, which is an inequality of the form (1.7), where  . Applying our Theorem 2.1 with the choice that
. Applying our Theorem 2.1 with the choice that  , we obtain an estimate of the difference
, we obtain an estimate of the difference  in the form (2.4), where
in the form (2.4), where  because
because  . Furthermore, by the definition of
. Furthermore, by the definition of  we see that
we see that

It follows that

since  . Thus, by (4.10),
. Thus, by (4.10),

Similarly, we get  and therefore
and therefore

Thus we conclude from (2.4) that  , implying that
, implying that  for all
for all  since
since  is strictly increasing. It proves the uniqueness.
is strictly increasing. It proves the uniqueness.
Remark 4.3.
If  or
or  in (4.8), the conclusion of the Corollary 4.2 also can be obtained.
in (4.8), the conclusion of the Corollary 4.2 also can be obtained.
Finally, we discuss the continuous dependence of solutions of BVP (4.1) on the given functions  , and
, and  . Consider a variation of BVP (4.1)
. Consider a variation of BVP (4.1)

where  is strictly increasing odd function satisfying
is strictly increasing odd function satisfying  for
for  ,
,  , and
, and  are functions satisfying
are functions satisfying  .
.
Corollary 4.4.
Let  be a function as assumed in the beginning of Section 4 and satisfy (4.2) and (4.8) on the same lattice
be a function as assumed in the beginning of Section 4 and satisfy (4.2) and (4.8) on the same lattice  as assumed in Corollary 4.2. Suppose that the three differences
as assumed in Corollary 4.2. Suppose that the three differences

are all sufficiently small. Then solution  of BVP (4.14) is sufficiently close to the solution
of BVP (4.14) is sufficiently close to the solution  of BVP (4.1).
of BVP (4.1).
Proof.
By Corollary 4.2, the solution  is unique. By the continuity and the strict monotonicity of
is unique. By the continuity and the strict monotonicity of  , we suppose that
, we suppose that

where  is a small number. By the equivalent difference equation (4.5) and the inequality (4.8) we get
is a small number. By the equivalent difference equation (4.5) and the inequality (4.8) we get

that is an inequality of the form (1.7). Applying Theorem 2.1 to (4.17), we obtain, for all  , that
, that

where  are given as in Theorem 2.1,
are given as in Theorem 2.1,

By (4.10) we see that  (
( ) as
) as  . It follows from (4.18) that
. It follows from (4.18) that  and hence
and hence  depends continuously on
depends continuously on  and
and  .
.
Remark 4.5.
Our requirement of the small difference  in Corollary 4.4 is stronger than the condition (iii) in [26, Theorem
in Corollary 4.4 is stronger than the condition (iii) in [26, Theorem  ], but it is easier to check than the condition of them.
], but it is easier to check than the condition of them.
References
Gronwall TH: Note on the derivatives with respect to a parameter of the solutions of a system of differential equations. Annals of Mathematics 1919,20(4):292-296. 10.2307/1967124
Bellman R: The stability of solutions of linear differential equations. Duke Mathematical Journal 1943, 10: 643-647. 10.1215/S0012-7094-43-01059-2
Agarwal RP, Deng S, Zhang W: Generalization of a retarded Gronwall-like inequality and its applications. Applied Mathematics and Computation 2005,165(3):599-612. 10.1016/j.amc.2004.04.067
Baĭnov D, Simeonov P: Integral Inequalities and Applications, Mathematics and Its Applications (East European Series). Volume 57. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+245.
Cheung W-S, Ma Q-H: On certain new Gronwall-Ou-Iang type integral inequalities in two variables and their applications. Journal of Inequalities and Applications 2005,10(4):347-361.
Lipovan O: Integral inequalities for retarded Volterra equations. Journal of Mathematical Analysis and Applications 2006,322(1):349-358. 10.1016/j.jmaa.2005.08.097
Ma Q-H, Yang E-H: On some new nonlinear delay integral inequalities. Journal of Mathematical Analysis and Applications 2000,252(2):864-878. 10.1006/jmaa.2000.7134
Mitrinović DS, Pečarić JE, Fink AM: Inequalities Involving Functions and Their Integrals and Derivatives, Mathematics and Its Applications (East European Series). Volume 53. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xvi+587.
Pachpatte BG: Inequalities for Differential and Integral Equations, Mathematics in Science and Engineering. Volume 197. Academic Press, San Diego, Calif, USA; 1998:x+611.
Wang W-S: A generalized retarded Gronwall-like inequality in two variables and applications to BVP. Applied Mathematics and Computation 2007,191(1):144-154. 10.1016/j.amc.2007.02.099
Wang W-S: A generalized sum-difference inequality and applications to partial difference equations. Advances in Difference Equations 2008, 2008:-12.
Wang W-S, Shen C-X: On a generalized retarded integral inequality with two variables. Journal of Inequalities and Applications 2008, 2008:-9.
Wang W-S: Estimation on certain nonlinear discrete inequality and applications to boundary value problem. Advances in Difference Equations 2009, 2009:-8.
Zhang W, Deng S: Projected Gronwall-Bellman's inequality for integrable functions. Mathematical and Computer Modelling 2001,34(3-4):393-402. 10.1016/S0895-7177(01)00070-X
Zheng K, Wu Y, Deng S: Nonlinear integral inequalities in two independent variables and their applications. Journal of Inequalities and Applications 2007, 2007:-11.
Hull TE, Luxemburg WAJ: Numerical methods and existence theorems for ordinary differential equations. Numerische Mathematik 1960, 2: 30-41. 10.1007/BF01386206
Pachpatte BG, Deo SG: Stability of discrete-time systems with retarded argument. Utilitas Mathematica 1973, 4: 15-33.
Willett D, Wong JSW: On the discrete analogues of some generalizations of Gronwall's inequality. Monatshefte für Mathematik 1965, 69: 362-367. 10.1007/BF01297622
Pachpatte BG: On some fundamental integral inequalities and their discrete analogues. Journal of Inequalities in Pure and Applied Mathematics 2001,2(2, article 15):1-13.
Dafermos CM: The second law of thermodynamics and stability. Archive for Rational Mechanics and Analysis 1979,70(2):167-179.
Pang PYH, Agarwal RP: On an integral inequality and its discrete analogue. Journal of Mathematical Analysis and Applications 1995,194(2):569-577. 10.1006/jmaa.1995.1318
Pachpatte BG: On some new inequalities related to certain inequalities in the theory of differential equations. Journal of Mathematical Analysis and Applications 1995,189(1):128-144. 10.1006/jmaa.1995.1008
Pachpatte BG: Inequalities for Finite Difference Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 247. Marcel Dekker, New York, NY, USA; 2002:x+514.
Pachpatte BG: Integral and Finite Difference Inequalities and Applications, North-Holland Mathematics Studies. Volume 205. Elsevier Science, Amsterdam, The Netherlands; 2006:x+309.
Cheung W-S: Some discrete nonlinear inequalities and applications to boundary value problems for difference equations. Journal of Difference Equations and Applications 2004,10(2):213-223. 10.1080/10236190310001604238
Cheung W-S, Ren J: Discrete non-linear inequalities and applications to boundary value problems. Journal of Mathematical Analysis and Applications 2006,319(2):708-724. 10.1016/j.jmaa.2005.06.064
Pinto M: Integral inequalities of Bihari-type and applications. Funkcialaj Ekvacioj 1990, 33: 387-430.
Acknowledgments
The authors thank Professor Weinian Zhang (Sichuan University) for his valuable discussion. The authors also thank the referees for their helpful comments and suggestions. This work is supported by the Natural Science Foundation of Guangxi Autonomous Region (200991265), by Scientific Research Foundation of the Education Department of Guangxi Autonomous Region of China (200707MS112) and by Foundation of Natural Science of Hechi University (2006A-N001) and Key Discipline of Applied Mathematics of Hechi University of China (200725).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, WS., Zhou, X. An Extension to Nonlinear Sum-Difference Inequality and Applications. Adv Differ Equ 2009, 486895 (2009). https://doi.org/10.1155/2009/486895
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/486895
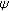 is a strictly increasing continuous function on
is a strictly increasing continuous function on 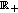 satisfying that
satisfying that  and
and 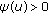 for all
for all 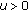 .
.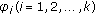 are continuous and positive functions on
are continuous and positive functions on  .
. on
on 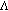 .
.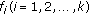 are nonnegative functions on
are nonnegative functions on 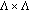 .
.