- Research Article
- Open access
- Published:
Sturm-Picone Comparison Theorem of Second-Order Linear Equations on Time Scales
Advances in Difference Equations volume 2009, Article number: 496135 (2009)
Abstract
This paper studies Sturm-Picone comparison theorem of second-order linear equations on time scales. We first establish Picone identity on time scales and obtain our main result by using it. Also, our result unifies the existing ones of second-order differential and difference equations.
1. Introduction
In this paper, we consider the following second-order linear equations:


where  and
and  are real and rd-continuous functions in
are real and rd-continuous functions in  Let
Let  be a time scale,
be a time scale,  be the forward jump operator in
be the forward jump operator in  ,
,  be the delta derivative, and
be the delta derivative, and  .
.
First we briefly recall some existing results about differential and difference equations. As we well know, in 1909, Picone [1] established the following identity.
Picone Identity
If  and
and  are the nontrivial solutions of
are the nontrivial solutions of

where  and
and  are real and continuous functions in
are real and continuous functions in  If
If  for
for  then
then

By (1.4), one can easily obtain the Sturm comparison theorem of second-order linear differential equations (1.3).
Sturm-Picone Comparison Theorem
Assume that  and
and  are the nontrivial solutions of (1.3) and
are the nontrivial solutions of (1.3) and  are two consecutive zeros of
are two consecutive zeros of  if
if

then  has at least one zero on
has at least one zero on 
Later, many mathematicians, such as Kamke, Leighton, and Reid [2–5] developed thier work. The investigation of Sturm comparison theorem has involved much interest in the new century [6, 7]. The Sturm comparison theorem of second-order difference equations

has been investigated in [8, Chapter 8], where  on
on  on
on  are integers, and
are integers, and  is the forward difference operator:
is the forward difference operator:  In 1995, Zhang [9] extended this result. But we will remark that in [8, Chapter 8] the authors employed the Riccati equation and a positive definite quadratic functional in their proof. Recently, the Sturm comparison theorem on time scales has received a lot of attentions. In [10, Chapter 4], the mathematicians studied
In 1995, Zhang [9] extended this result. But we will remark that in [8, Chapter 8] the authors employed the Riccati equation and a positive definite quadratic functional in their proof. Recently, the Sturm comparison theorem on time scales has received a lot of attentions. In [10, Chapter 4], the mathematicians studied

where  and
and  for
for  is the nabla derivative, and they get the Sturm comparison theorem. We will make use of Picone identity on time scales to prove the Sturm-Picone comparison theorem of (1.1) and (1.2).
is the nabla derivative, and they get the Sturm comparison theorem. We will make use of Picone identity on time scales to prove the Sturm-Picone comparison theorem of (1.1) and (1.2).
This paper is organized as follows. Section 2 introduces some basic concepts and fundamental results about time scales, which will be used in Section 3. In Section 3 we first give the Picone identity on time scales, then we will employ this to prove our main result: Sturm-Picone comparison theorem of (1.1) and (1.2) on time scales.
2. Preliminaries
In this section, some basic concepts and some fundamental results on time scales are introduced.
Let  be a nonempty closed subset. Define the forward and backward jump operators
be a nonempty closed subset. Define the forward and backward jump operators  by
by

where  ,
,  . A point
. A point  is called right-scattered, right-dense, left-scattered, and left-dense if
is called right-scattered, right-dense, left-scattered, and left-dense if  , and
, and  respectively. We put
respectively. We put  if
if  is unbounded above and
is unbounded above and  otherwise. The graininess functions
otherwise. The graininess functions  are defined by
are defined by

Let  be a function defined on
be a function defined on  .
.  is said to be (delta) differentiable at
is said to be (delta) differentiable at  provided there exists a constant
provided there exists a constant  such that for any
such that for any  , there is a neighborhood
, there is a neighborhood  of
of  (i.e.,
(i.e.,  for some
for some  ) with
) with

In this case, denote  . If
. If  is (delta) differentiable for every
is (delta) differentiable for every  , then
, then  is said to be (delta) differentiable on
is said to be (delta) differentiable on  . If
. If  is differentiable at
is differentiable at  , then
, then

If  for all
for all  , then
, then  is called an antiderivative of
is called an antiderivative of  on
on  . In this case, define the delta integral by
. In this case, define the delta integral by

Moreover, a function  defined on
defined on  is said to be rd-continuous if it is continuous at every right-dense point in
is said to be rd-continuous if it is continuous at every right-dense point in  and its left-sided limit exists at every left-dense point in
and its left-sided limit exists at every left-dense point in  .
.
For convenience, we introduce the following results ([11, Chapter 1], [12, Chapter 1], and [13, Lemma  ]), which are useful in the paper.
]), which are useful in the paper.
Lemma 2.1.
Let  and
and  .
.
-
(i)
If
 is differentiable at
is differentiable at  , then
, then 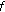 is continuous at
is continuous at 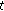 .
. -
(ii)
If
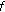 and
and 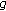 are differentiable at
are differentiable at  , then
, then 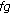 is differentiable at
is differentiable at  and
and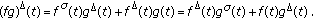 (2.6)
(2.6) -
(iii)
If
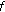 and
and 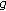 are differentiable at
are differentiable at 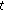 , and
, and 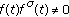 , then
, then  is differentiable at
is differentiable at  and
and (2.7)
(2.7) -
(iv)
If
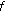 is rd-continuous on
is rd-continuous on 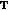 , then it has an antiderivative on
, then it has an antiderivative on  .
.
Definition 2.2.
A function  is said to be right-increasing at
is said to be right-increasing at  provided
provided
-
(i)
 in the case that
in the case that 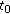 is right-scattered;
is right-scattered; -
(ii)
there is a neighborhood
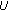 of
of  such that
such that  for all
for all 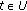 with
with 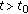 in the case that
in the case that 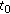 is right-dense.
is right-dense.
If the inequalities for  are reversed in (i) and (ii),
are reversed in (i) and (ii),  is said to be right-decreasing at
is said to be right-decreasing at  .
.
The following result can be directly derived from (2.4).
Lemma 2.3.
Assume that  is differentiable at
is differentiable at  If
If  then
then  is right-increasing at
is right-increasing at  ; and if
; and if  , then
, then  is right-decreasing at
is right-decreasing at  .
.
Definition 2.4.
One says that a solution  of (1.1) has a generalized zero at
of (1.1) has a generalized zero at  if
if  or, if
or, if  is right-scattered and
is right-scattered and  Especially, if
Especially, if  then we say
then we say  has a node at
has a node at 
A function  is called regressive if
is called regressive if

Hilger [14] showed that for  and rd-continuous and regressive
and rd-continuous and regressive  , the solution of the initial value problem
, the solution of the initial value problem

is given by  , where
, where

The development of the theory uses similar arguments and the definition of the nabla derivative (see [10, Chapter 3]).
3. Main Results
In this section, we give and prove the main results of this paper.
First, we will show that the following second-order linear equation:

can be rewritten as (1.1).
Theorem 3.1.
If  and
and  is continuous, then (3.1) can be written in the form of (1.1), with
is continuous, then (3.1) can be written in the form of (1.1), with

Proof.
Multiplying both sides of (3.1) by  , we get
, we get

where we used Lemma 2.1. This equation is in the form of (1.1) with  and
and  as desired.
as desired.
Lemma 3.2 (Picone Identity).
Let  and
and  be the nontrivial solutions of (1.1) and (1.2) with
be the nontrivial solutions of (1.1) and (1.2) with  and
and  for
for  If
If  has no generalized zeros on
has no generalized zeros on  then the following identity holds:
then the following identity holds:

Proof.
We first divide the left part of (3.4) into two parts

From (1.1) and the product rule (Lemma 2.1(ii), we have

It follows from (1.2), (2.4), product and quotient rules (Lemma 2.1(ii), (iii) and the assumption that  has no generalized zeros on
has no generalized zeros on  that
that

Combining  and
and  , we get (3.4). This completes the proof.
, we get (3.4). This completes the proof.
Now, we turn to proving the main result of this paper.
Theorem 3.3 (Sturm-Picone Comparison Theorem).
Suppose that  and
and  are the nontrivial solutions of (1.1) and (1.2), and
are the nontrivial solutions of (1.1) and (1.2), and  are two consecutive generalized zeros of
are two consecutive generalized zeros of  if
if

then  has at least one generalized zero on
has at least one generalized zero on 
Proof.
Suppose to the contrary,  has no generalized zeros on
has no generalized zeros on  and
and  for all
for all 
Case 1.
Suppose  are two consecutive zeros of
are two consecutive zeros of  . Then by Lemma 3.2, (3.4) holds and integrating it from
. Then by Lemma 3.2, (3.4) holds and integrating it from  to
to  we get
we get

Noting that  we have
we have

Hence, by (3.9) and  we have
we have

which is a contradiction. Therefore, in Case 1,  has at least one generalized zero on
has at least one generalized zero on 
Case 2.
Suppose  is a zero of
is a zero of  is a node of
is a node of  and
and  It follows from the assumption that
It follows from the assumption that  has no generalized zeros on
has no generalized zeros on  and that
and that  for all
for all  that
that  Hence by (2.4) and
Hence by (2.4) and  on
on  , we have
, we have

By integration, it follows from (3.12) and  that
that

So, from (3.9) and above argument we obtain that

which is a contradiction, too. Hence, in Case 2,  has at least one generalized zero on
has at least one generalized zero on  .
.
Case 3.
Suppose  is a node of
is a node of  and
and  is a generalized zero of
is a generalized zero of  Similar to the discussion of (3.12), we have
Similar to the discussion of (3.12), we have

which implies

(i)If  is a node of
is a node of  then
then  Hence, we have (3.12), that is,
Hence, we have (3.12), that is,

(ii)If  is a zero of
is a zero of  then
then

It follows from (3.4) and Lemma 2.3 that

is right-increasing on  Hence, from (i) and (ii) that
Hence, from (i) and (ii) that

which implies

From (3.16), (3.21), and (2.4), we have

Further, it follows from (1.1), (1.2), product rule (Lemma 2.1(ii), and (3.22) that

If  and from
and from  ,
,  , and
, and  we have
we have

This contradicts (3.22). Note that  . It follows from
. It follows from  , (3.23), and (3.24) that
, (3.23), and (3.24) that

On the other hand, it follows from  and
and  are solutions of (1.1) and (1.2) that
are solutions of (1.1) and (1.2) that

Combining the above two equations we obtain

It follows from (3.27) and (2.4) that

Hence, from  and (3.21), we get
and (3.21), we get

By referring to  and
and  it follows that
it follows that

which contradicts 
It follows from the above discussion that  has at least one generalized zero on
has at least one generalized zero on  This completes the proof.
This completes the proof.
Remark 3.4.
If  then Theorem 3.3 reduces to classical Sturm comparison theorem.
then Theorem 3.3 reduces to classical Sturm comparison theorem.
Remark 3.5.
In the continuous case:  . This result is the same as Sturm-Picone comparison theorem of second-order differential equations (see Section 1).
. This result is the same as Sturm-Picone comparison theorem of second-order differential equations (see Section 1).
Remark 3.6.
In the discrete case:  . This result is the same as Sturm comparison theorem of second-order difference equations (see [8, Chapter 8]).
. This result is the same as Sturm comparison theorem of second-order difference equations (see [8, Chapter 8]).
Example 3.7.
Consider the following three specific cases:

By Theorem 3.3, we have if  and
and  are the nontrivial solutions of (1.1) and (1.2),
are the nontrivial solutions of (1.1) and (1.2),  are two consecutive generalized zeros of
are two consecutive generalized zeros of  and
and  then
then  has at least one generalized zero on
has at least one generalized zero on  Obviously, the above three cases are not continuous and not discrete. So the existing results for the differential and difference equations are not available now.
Obviously, the above three cases are not continuous and not discrete. So the existing results for the differential and difference equations are not available now.
By Remarks 3.4–3.6 and Example 3.7, the Sturm comparison theorem on time scales not only unifies the results in both the continuous and the discrete cases but also contains more complicated time scales.
References
Picone M: Sui valori eccezionali di un parametro da cui dipend unèquazione differenziale linear ordinaria del second ordine. JMPA 1909, 11: 1-141.
Kamke E: A new proof of Sturm's comparison theorems. The American Mathematical Monthly 1939, 46: 417-421. 10.2307/2303035
Leighton W: Comparison theorems for linear differential equations of second order. Proceedings of the American Mathematical Society 1962, 13: 603-610. 10.1090/S0002-9939-1962-0140759-0
Leighton W: Some elementary Sturm theory. Journal of Differential Equations 1968, 4: 187-193. 10.1016/0022-0396(68)90035-1
Reid WT: A comparison theorem for self-adjoint differential equations of second order. Annals of Mathematics 1957, 65: 197-202. 10.2307/1969673
Zhuang R: Sturm comparison theorem of solution for second order nonlinear differential equations. Annals of Differential Equations 2003,19(3):480-486.
Zhuang R-K, Wu H-W: Sturm comparison theorem of solution for second order nonlinear differential equations. Applied Mathematics and Computation 2005,162(3):1227-1235. 10.1016/j.amc.2004.03.004
Kelley WG, Peterson AC: Difference Equations: An Introduction with Applications. 2nd edition. Harcourt/Academic Press, San Diego, Calif, USA; 2001:x+403.
Zhang BG: Sturm comparison theorem of difference equations. Applied Mathematics and Computation 1995,72(2-3):277-284. 10.1016/0096-3003(94)00201-E
Bohner M, Peterso A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Hilger S: Special functions, Laplace and Fourier transform on measure chains. Dynamic Systems and Applications 1999,8(3-4):471-488.
Acknowledgments
Many thanks to Alberto Cabada (the editor) and the anonymous reviewer(s) for helpful comments and suggestions. This research was supported by the Natural Scientific Foundation of Shandong Province (Grant Y2007A27), (Grant Y2008A28), the Fund of Doctoral Program Research of University of Jinan (B0621), and the Natural Science Fund Project of Jinan University (XKY0704).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, C., Sun, S. Sturm-Picone Comparison Theorem of Second-Order Linear Equations on Time Scales. Adv Differ Equ 2009, 496135 (2009). https://doi.org/10.1155/2009/496135
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/496135
 is differentiable at
is differentiable at  , then
, then 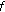 is continuous at
is continuous at 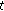 .
. and
and 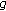 are differentiable at
are differentiable at  , then
, then 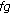 is differentiable at
is differentiable at  and
and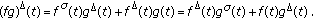
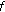 and
and 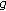 are differentiable at
are differentiable at 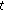 , and
, and 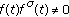 , then
, then  is differentiable at
is differentiable at  and
and
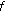 is rd-continuous on
is rd-continuous on 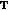 , then it has an antiderivative on
, then it has an antiderivative on  .
. in the case that
in the case that 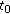 is right-scattered;
is right-scattered; of
of  such that
such that  for all
for all 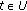 with
with 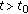 in the case that
in the case that 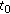 is right-dense.
is right-dense.