- Research Article
- Open access
- Published:
Almost Automorphic Solutions of Difference Equations
Advances in Difference Equations volume 2009, Article number: 591380 (2009)
Abstract
We study discrete almost automorphic functions (sequences) defined on the set of integers with values in a Banach space  . Given a bounded linear operator
. Given a bounded linear operator  defined on
defined on  and a discrete almost automorphic function
and a discrete almost automorphic function  , we give criteria for the existence of discrete almost automorphic solutions of the linear difference equation
, we give criteria for the existence of discrete almost automorphic solutions of the linear difference equation  . We also prove the existence of a discrete almost automorphic solution of the nonlinear difference equation
. We also prove the existence of a discrete almost automorphic solution of the nonlinear difference equation  assuming that
assuming that  is discrete almost automorphic in
is discrete almost automorphic in  for each
for each  , satisfies a global Lipschitz type condition, and takes values on
, satisfies a global Lipschitz type condition, and takes values on  .
.
1. Introduction
The theory of difference equations has grown at an accelerated pace in the last decades. It now occupies a central position in applicable analysis and plays an important role in mathematics as a whole.
A very important aspect of the qualitative study of the solutions of difference equations is their periodicity. Periodic difference equations and systems have been treated, among others, by Agarwal and Popenda [1], Corduneanu [2], Halanay [3], Pang and Agarwal [4], Sugiyama [5], Elaydi [6], and Agarwal [7]. Almost periodicity of a discrete function was first introduced by Walther [8, 9] and then by Corduneanu [2]. Recently, several papers [10–16] are devoted to study existence of almost periodic solutions of difference equations.
Discrete almost automorphic functions, a class of functions which are more general than discrete almost periodic ones, were recently introduced in [17, Definition 2.6] in connection with the study of (continuous) almost automorphic bounded mild solutions of differential equations. See also [18, 19]. However, the concept of discrete almost automorphic functions has not been explored in the theory of difference equations. In this paper, we first review their main properties, most of which are discrete versions of N'Guérékata's work in [20, 21], and then we give an application in the study of existence of discrete almost automorphic solutions of linear and nonlinear difference equations.
The theory of continuous almost automorphic functions was introduced by Bochner, in relation to some aspects of differential geometry [22–25]. A unified and homogeneous exposition of the theory and its applications was first given by N'Guérékata in his book [21]. After that, there has been a real resurgent interest in the study of almost automorphic functions.
Important contributions to the theory of almost automorphic functions have been obtained, for example, in the papers [26–33], in the books [20, 21, 32] (concerning almost automorphic functions with values in Banach spaces), and in [34] (concerning almost automorphy on groups). Also, the theory of almost automorphic functions with values in fuzzy-number-type spaces was developed in [35] (see also [20, Chapter 4]). Recently, in [36, 37], the theory of almost automorphic functions with values in a locally convex space (Fréchet space) and a  -Fréchet space has been developed.
-Fréchet space has been developed.
The range of applications of almost automorphic functions includes at present linear and nonlinear evolution equations, integro-differential and functional-differential equations, and dynamical systems. A recent reference is the book [20].
This paper is organized as follows. In Section 2, we present the definition of discrete almost automorphic functions (sequences) as a natural generalization of discrete almost periodic functions, and then we give some basic and related properties for our purposes. In Section 3, we discuss the existence of almost automorphic solutions of first-order linear difference equations. In Section 4, we discuss the existence of almost automorphic solutions of nonlinear difference equations of the form  , where
, where  is a bounded operator defined on a Banach space
is a bounded operator defined on a Banach space  .
.
2. The Basic Theory
Let  be a real or complex Banach space. We recall that a function
be a real or complex Banach space. We recall that a function  is said to be discrete almost periodic if for any positive
is said to be discrete almost periodic if for any positive  there exists a positive integer
there exists a positive integer  such that any set consisting of
such that any set consisting of  consecutive integers contains at least one integer
consecutive integers contains at least one integer  with the property that
with the property that

In the above definition  is called an
is called an  -almost period of
-almost period of  or an
or an  -translation number. We denote by
-translation number. We denote by  the set of discrete almost periodic functions.
the set of discrete almost periodic functions.
Bochner's criterion:  is a discrete almost periodic function if and only if (N) for any integer sequence
is a discrete almost periodic function if and only if (N) for any integer sequence  , there exists a subsequence
, there exists a subsequence  such that
such that  converges uniformly on
converges uniformly on  as
as  . Furthermore, the limit sequence is also a discrete almost periodic function.
. Furthermore, the limit sequence is also a discrete almost periodic function.
The proof can be found in [38, Theorem 1.26, pages 45-46]. Observe that functions with the property (N) are also called normal in literature (cf. [7, page 72] or [38]).
The above characterization, as well as the definition of continuous almost automorphic functions (cf. [21]), motivates the following definition.
Definition 2.1.
Let  be a (real or complex) Banach space. A function
be a (real or complex) Banach space. A function  is said to be discrete almost automorphic if for every integer sequence
is said to be discrete almost automorphic if for every integer sequence  , there exists a subsequence
, there exists a subsequence  such that
such that

is well defined for each  and
and

for each 
Remark 2.2.
-
(i)
If
 is a continuous almost automorphic function in
is a continuous almost automorphic function in 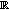 then
then  is discrete almost automorphic.
is discrete almost automorphic. -
(ii)
If the convergence in Definition 2.1 is uniform on
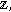 then we get discrete almost periodicity.
then we get discrete almost periodicity.
We denote by  the set of discrete almost automorphic functions. Such as the continuous case we have that discrete almost automorphicity is a more general concept than discrete almost periodicity; that is,
the set of discrete almost automorphic functions. Such as the continuous case we have that discrete almost automorphicity is a more general concept than discrete almost periodicity; that is,

Remark 2.3.
Examples of discrete almost automorphic functions which are not discrete almost periodic were first constructed by Veech [39]. In fact, note that the examples introduced in [39] are not on the additive group  but on its discrete subgroup
but on its discrete subgroup  A concrete example, provided later in [25, Theorem 1] by Bochner, is
A concrete example, provided later in [25, Theorem 1] by Bochner, is

where  is any nonrational real number.
is any nonrational real number.
Discrete almost automorphic functions have the following fundamental properties.
Theorem 2.4.
Let  be discrete almost automorphic functions; then, the following assertions are valid:
be discrete almost automorphic functions; then, the following assertions are valid:
-
(i)
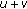 is discrete almost automorphic;
is discrete almost automorphic; -
(ii)
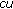 is discrete almost automorphic for every scalar
is discrete almost automorphic for every scalar  ;
; -
(iii)
for each fixed
 in
in  the function
the function 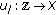 defined by
defined by  is discrete almost automorphic;
is discrete almost automorphic; -
(iv)
the function
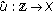 defined by
defined by 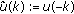 is discrete almost automorphic;
is discrete almost automorphic; -
(v)
 ; that is,
; that is,  is a bounded function;
is a bounded function; -
(vi)
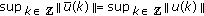 , where
, where (2.6)
(2.6)
Proof.
The proof of all statements follows the same lines as in the continuous case (see [21, Theorem 2.1.3]), and therefore is omitted.
As a consequence of the above theorem, the space of discrete almost automorphic functions provided with the norm

becomes a Banach space. The proof is straightforward and therefore omitted.
Theorem 2.5.
Let  be Banach spaces, and let
be Banach spaces, and let  a discrete almost automorphic function. If
a discrete almost automorphic function. If  is a continuous function, then the composite function
is a continuous function, then the composite function  is discrete almost automorphic.
is discrete almost automorphic.
Proof.
Let  be a sequence in
be a sequence in  , and since
, and since  there exists a subsequence
there exists a subsequence  of
of  such that
such that  is well defined for each
is well defined for each  and
and  for each
for each  Since
Since  is continuous, we have
is continuous, we have  In similar way, we have
In similar way, we have  therefore
therefore  is in
is in 
Corollary 2.6.
If  is a bounded linear operator on
is a bounded linear operator on  and
and  is a discrete almost automorphic function, then
is a discrete almost automorphic function, then  ,
,  is also discrete almost automorphic.
is also discrete almost automorphic.
Theorem 2.7.
Let  and
and  be discrete almost automorphic. Then
be discrete almost automorphic. Then  defined by
defined by  ,
,  is also discrete almost automorphic.
is also discrete almost automorphic.
Proof.
Let  be a sequence in
be a sequence in  . There exists a subsequence
. There exists a subsequence  of
of  such that
such that  is well defined for each
is well defined for each  and
and  for each
for each  Also we have
Also we have  that is well defined for each
that is well defined for each  and
and  for each
for each  . The proof now follows from Theorem 2.4, and the identities
. The proof now follows from Theorem 2.4, and the identities

which are valid for all  .
.
For applications to nonlinear difference equations the following definition, of discrete almost automorphic function depending on one parameter, will be useful.
Definition 2.8.
A function  is said to be discrete almost automorphic in
is said to be discrete almost automorphic in  for each
for each  if for every sequence of integers numbers
if for every sequence of integers numbers  there exists a subsequence
there exists a subsequence  such that
such that

is well defined for each  ,
,  , and
, and

for each  and
and  .
.
The proof of the following result is omitted (see [21, Section 2.2]).
Theorem 2.9.
If  are discrete almost automorphic functions in
are discrete almost automorphic functions in  for each
for each  in
in  then the followings are true.
then the followings are true.
-
(i)
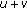 is discrete almost automorphic in
is discrete almost automorphic in 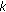 for each
for each  in
in 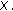
-
(ii)
 is discrete almost automorphic in
is discrete almost automorphic in  for each
for each  in
in  where
where  is an arbitrary scalar.
is an arbitrary scalar. -
(iii)
 for each
for each  in
in  .
. -
(iv)
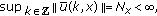 for each
for each  in
in  where
where  is the function in Definition 2.8.
is the function in Definition 2.8.
The following result will be used to study almost automorphy of solution of nonlinear difference equations.
Theorem 2.10.
Let  be discrete almost automorphic in
be discrete almost automorphic in  for each
for each  in X, and satisfy a Lipschitz condition in
in X, and satisfy a Lipschitz condition in  uniformly in
uniformly in  ; that is,
; that is,

Suppose  is discrete almost automorphic, then the function
is discrete almost automorphic, then the function  defined by
defined by  is discrete almost automorphic.
is discrete almost automorphic.
Proof.
Let  be a sequence in
be a sequence in  . There exists a subsequence
. There exists a subsequence  of
of  such that
such that  for all
for all  ,
,  and
and  for each
for each  ,
,  . Also we have
. Also we have  is well defined for each
is well defined for each  and
and  for each
for each  . Since the function
. Since the function  is Lipschitz, using the identities
is Lipschitz, using the identities

valid for all  we get the desired proof.
we get the desired proof.
We will denote  the space of the discrete almost automorphics functions in
the space of the discrete almost automorphics functions in  for each
for each  in
in  .
.
Let  denote the forward difference operator of the first-order, that is, for each
denote the forward difference operator of the first-order, that is, for each  and
and  ,
,  .
.
Theorem 2.11.
Let  be a discrete almost automorphic function, then
be a discrete almost automorphic function, then  is also discrete almost automorphic.
is also discrete almost automorphic.
Proof.
Since  then by (i) and (iii) in Theorem 2.4, we have that
then by (i) and (iii) in Theorem 2.4, we have that  is discrete almost automorphic.
is discrete almost automorphic.
More important is the following converse result, due to Basit [40, Theorem 1] (see also [17, Lemma 2.8]). Recall that  is defined as the space of all sequences converging to zero.
is defined as the space of all sequences converging to zero.
Theorem 2.12.
Let  be a Banach space that does not contain any subspace isomorphic to
be a Banach space that does not contain any subspace isomorphic to  Let
Let  and assume that
and assume that

is discrete almost automorphic. Then  is also discrete almost automorphic.
is also discrete almost automorphic.
As is well known a uniformly convex Banach space does not contain any subspace isomorphic to  . In particular, every finite-dimensional space does not contain any subspace isomorphic to
. In particular, every finite-dimensional space does not contain any subspace isomorphic to  . The following result will be the key in the study of discrete almost automorphic solutions of linear and nonlinear difference equations.
. The following result will be the key in the study of discrete almost automorphic solutions of linear and nonlinear difference equations.
Theorem 2.13.
Let  be a summable function, that is,
be a summable function, that is,

Then for any discrete almost automorphic function  the function
the function  defined by
defined by

is also discrete almost automorphic.
Proof.
Let  be a arbitrary sequence of integers numbers. Since
be a arbitrary sequence of integers numbers. Since  is discrete almost automorphic there exists a subsequence
is discrete almost automorphic there exists a subsequence  of
of  such that
such that

is well defined for each  and
and

for each  . Note that
. Note that

then, by Lebesgue's dominated convergence theorem, we obtain

In similar way, we prove

and then  is discrete almost automorphic.
is discrete almost automorphic.
Remark 2.14.
-
(i)
The same conclusions of the previous results holds in case of the finite convolution
 (2.21)
(2.21)
and the convolution

-
(ii)
The results are true if we consider an operator valued function
 such that
such that  (2.23)
(2.23)
A typical example is  , where
, where  satisfies
satisfies  .
.
3. Almost Automorphic Solutions of First-Order Linear Difference Equations
Difference equations usually describe the evolution of certain phenomena over the course of time. In this section we deal with those equations known as the first-order linear difference equations. These equations naturally apply to various fields, like biology (the study of competitive species in population dynamics), physics (the study of motions of interacting bodies), the study of control systems, neurology, and electricity; see [6, Chapter 3].
We are interested in finding discrete almost automorphic solutions of the following system of first-order linear difference equations, written in vector form

where  is a matrix or, more generally, a bounded linear operator defined on a Banach space
is a matrix or, more generally, a bounded linear operator defined on a Banach space  and
and  is in
is in  . Note that (3.1) is equivalent to
. Note that (3.1) is equivalent to

where  We begin studying the scalar case. We denote
We begin studying the scalar case. We denote  .
.
Theorem 3.1.
Let  be a Banach space. If
be a Banach space. If  and
and  is discrete almost automorphic, then there is a discrete almost automorphic solution of (3.2) given by
is discrete almost automorphic, then there is a discrete almost automorphic solution of (3.2) given by
-
(i)
 in case
in case 
-
(ii)
 in case
in case 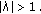
Proof.
-
(i)
Define
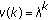 . Then
. Then  and hence, by Theorem 2.13, we obtain
and hence, by Theorem 2.13, we obtain  Next, we note that
Next, we note that  is solution of (3.2) because
is solution of (3.2) because 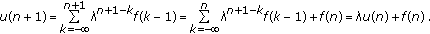 (3.3)
(3.3) -
(ii)
Define
 and since
and since 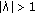 we have
we have 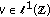 . It follows, by Theorem 2.13, that
. It follows, by Theorem 2.13, that 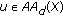 . Finally, we check that
. Finally, we check that  is solution of (3.2) as follows:
is solution of (3.2) as follows: 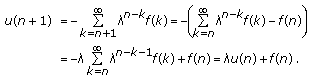 (3.4)
(3.4)
As a consequence of the previous theorem, we obtain the following result in case of a matrix  .
.
Theorem 3.2.
Suppose  is a constant
is a constant  matrix with eigenvalues
matrix with eigenvalues  . Then for any function
. Then for any function  there is a discrete almost automorphic solution of (3.2).
there is a discrete almost automorphic solution of (3.2).
Proof.
It is well known that there exists a nonsingular matrix  such that
such that  is an upper triangular matrix. In (3.2) we use now the substitution
is an upper triangular matrix. In (3.2) we use now the substitution  to obtain
to obtain

Obviously, the system (3.5) is of the form as (3.2) with  a discrete almost automorphic function. The general case of an arbitrary matrix
a discrete almost automorphic function. The general case of an arbitrary matrix  can now be reduced to the scalar case. Indeed, the last equation of the system (3.5) is of the form
can now be reduced to the scalar case. Indeed, the last equation of the system (3.5) is of the form

where  is a complex number and
is a complex number and  is a discrete almost automorphic function. Hence, all we need to show is that any solution
is a discrete almost automorphic function. Hence, all we need to show is that any solution  of (3.6) is discrete almost automorphic. But this is the content of Theorem 3.1. It then implies that the
of (3.6) is discrete almost automorphic. But this is the content of Theorem 3.1. It then implies that the  th component
th component  of the solution
of the solution  of (3.5) is discrete almost automorphic. Then substituting
of (3.5) is discrete almost automorphic. Then substituting  in the
in the  th equation of (3.5) we obtain again an equation of the form (3.6) for
th equation of (3.5) we obtain again an equation of the form (3.6) for  and so on. The proof is complete.
and so on. The proof is complete.
Remark 3.3.
The procedure in the Proof of Theorem 3.2 is called "Method of Reduction" and introduced, in the continuous case, by N'Guérékata [20, Remark 6.2.2]. See also [41, 42]. In the discrete case, it was used earlier by Agarwal (cf. [7, Theorem 2.10.1]).
As an application of the above Theorem and [7, Theorem 5.2.4] we obtain the following Corollary.
Corollary 3.4.
Assume that  is a constant
is a constant  matrix with eigenvalues
matrix with eigenvalues  , and suppose that
, and suppose that  is such that
is such that

for all large  , where
, where  and
and  . Then there is a discrete almost automorphic solution
. Then there is a discrete almost automorphic solution  of (3.2), which satisfies
of (3.2), which satisfies

for some  .
.
We can replace  in Theorem 3.1 by a general bounded operator
in Theorem 3.1 by a general bounded operator  and use (ii) of Remark 2.14 in the proof of the first part of Theorem 3.1, to obtain the following result.
and use (ii) of Remark 2.14 in the proof of the first part of Theorem 3.1, to obtain the following result.
Theorem 3.5.
Let  be a Banach space, and let
be a Banach space, and let  such that
such that  . Let
. Let  . Then there is a discrete almost automorphic solution of (3.2).
. Then there is a discrete almost automorphic solution of (3.2).
We can also prove the following result.
Theorem 3.6.
Let  be a Banach space. Suppose
be a Banach space. Suppose  and
and  where the complex numbers
where the complex numbers  are mutually distinct with
are mutually distinct with  , and
, and  forms a complex system
forms a complex system  of mutually disjoint projections on
of mutually disjoint projections on  . Then (3.2) admits a discrete almost automorphic solution.
. Then (3.2) admits a discrete almost automorphic solution.
Proof.
Let  be fixed. Applying the projection
be fixed. Applying the projection  to (3.2) we obtain
to (3.2) we obtain

By Corollary 2.6 we have  since
since  is bounded. Therefore, by Theorem 3.1, we get
is bounded. Therefore, by Theorem 3.1, we get  . We conclude that
. We conclude that  as a finite sum of discrete almost periodic functions.
as a finite sum of discrete almost periodic functions.
The following important related result corresponds to the general Banach space setting. It is due to Minh et al. [17, Theorem 2.14]. We denote by  the part of the spectrum of
the part of the spectrum of  on
on  .
.
Theorem 3.7.
Let  be a Banach space that does not contain any subspace isomorphic to
be a Banach space that does not contain any subspace isomorphic to  . Assume that
. Assume that  is countable, and let
is countable, and let  . Then each bounded solution of (3.2) is discrete almost automorphic.
. Then each bounded solution of (3.2) is discrete almost automorphic.
We point out that in the finite dimensional case, the above result extend Corduneanu's Theorem on discrete almost periodic functions (see [7, Theorem 2.10.1, page 73]) to discrete almost automorphic functions. We state here the result for future reference.
Theorem 3.8.
Let  . Then a solution of (3.2) is discrete almost automorphic if and only if it is bounded.
. Then a solution of (3.2) is discrete almost automorphic if and only if it is bounded.
Interesting examples of application of Theorem 3.7 are given in [19, Theorems 3.4 and 3.7], concerning the existence of almost automorphic solutions of differential equations with piecewise constant arguments of the form

where  is a bounded linear operator on a Banach space
is a bounded linear operator on a Banach space  and
and  is the largest integer function. These results are based in the following connection between discrete and continuous almost automorphic functions.
is the largest integer function. These results are based in the following connection between discrete and continuous almost automorphic functions.
Theorem 3.9.
Let  and
and  be a bounded solution of (3.10) on
be a bounded solution of (3.10) on  . Then
. Then  is almost automorphic if and only if the sequence
is almost automorphic if and only if the sequence  is almost automorphic.
is almost automorphic.
For a proof, see [19, Lemma 3.3]. A corresponding result for compact almost automorphic functions is also true (see [19, Lemma 3.6]).
We finish this section with the following simple example concerning the heat equation (cf. [6, page 157]).
Example 3.10.
Consider the distribution of heat through a thin bar composed by a homogeneous material. Let  be
be  equidistant points on the bar. Let
equidistant points on the bar. Let  be the temperature at time
be the temperature at time  at the point
at the point  ,
,  Under certain conditions one may derive the equation
Under certain conditions one may derive the equation

where the vector  consists of the components
consists of the components  ,
,  , and
, and  is a tridiagonal Toeplitz matrix. Its eigenvalues may be found by the formula
is a tridiagonal Toeplitz matrix. Its eigenvalues may be found by the formula

where  is a constant of proportionality concerning the difference of temperature between the point
is a constant of proportionality concerning the difference of temperature between the point  and the nearby points
and the nearby points  and
and  (see [6]). Assuming
(see [6]). Assuming

we obtain  for all eigenvalues
for all eigenvalues  of
of  . For each
. For each  , Theorem 3.5 then implies that, for
, Theorem 3.5 then implies that, for  , there is a discrete almost automorphic solution of (3.11). On the other hand, Theorem 3.7 implies that, without restriction on
, there is a discrete almost automorphic solution of (3.11). On the other hand, Theorem 3.7 implies that, without restriction on  , each bounded solution of (3.11) is discrete almost automorphic.
, each bounded solution of (3.11) is discrete almost automorphic.
4. Almost Automorphic Solutions of Semilinear Difference Equations
We want to find conditions under which it is possible to find discrete almost automorphic solutions to the equation

where  is a bounded linear operator defined on a Banach space
is a bounded linear operator defined on a Banach space  and
and  .
.
Our main result in this section is the following theorem for the scalar case.
Theorem 4.1.
Let  and
and  be discrete almost automorphic in
be discrete almost automorphic in  for each
for each  . Suppose that
. Suppose that  satisfies the following Lipschitz type condition
satisfies the following Lipschitz type condition

Then (4.1) have a unique discrete almost automorphic solution satisfying
-
(i)
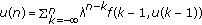 in case
in case  , and
, and -
(ii)
 in case
in case 
Proof.
Case  : we define the operator
: we define the operator  by
by

Since  and
and  satisfies (4.2), we obtain by Theorem 2.10 that
satisfies (4.2), we obtain by Theorem 2.10 that  is in
is in  . So
. So  is well-defined thanks to Theorem 2.13. Now, given
is well-defined thanks to Theorem 2.13. Now, given  we have
we have

Since  we obtain that the function
we obtain that the function  is a contraction. Then there exists a unique function
is a contraction. Then there exists a unique function  in
in  such that
such that  . That is,
. That is,  satisfies
satisfies  and hence
and hence  is solution of (4.1) (cf. the proof of (i) in Theorem 3.1).
is solution of (4.1) (cf. the proof of (i) in Theorem 3.1).
Case  : we define
: we define  by
by

and with similar arguments as in the previous case we obtain that  is well-defined. Now, given
is well-defined. Now, given  we have
we have

Therefore  is a contraction, and then there exists a unique function
is a contraction, and then there exists a unique function  such that
such that  . The function
. The function  satisfies
satisfies

and hence is a solution of (4.1) (cf. the proof of (ii) in Theorem 3.1).
In the particular case  we obtain the following corollary.
we obtain the following corollary.
Corollary 4.2.
Let  . Suppose that
. Suppose that  satisfies a Lipschitz condition
satisfies a Lipschitz condition

Then for each  , (4.1) have a unique discrete almost automorphic solution whenever
, (4.1) have a unique discrete almost automorphic solution whenever  or
or  .
.
The case of a bounded operator  can be treated assuming extra conditions on the operator. The proof of the next result follows the same lines of the first part in the proof of Theorem 4.1, using (ii) of Remark 2.14.
can be treated assuming extra conditions on the operator. The proof of the next result follows the same lines of the first part in the proof of Theorem 4.1, using (ii) of Remark 2.14.
Theorem 4.3.
Let  and suppose that
and suppose that  is such that
is such that

Then (4.1) have a unique discrete almost automorphic solution whenever  .
.
5. Conclusion and Future Directions
The aim of the present paper is to present for the first time a brief exposition of the theory of discrete almost automorphic funtions and its application to the field of difference equations in abstract spaces. We first state, for future reference, several results which can be directly deduced from the continuous case, and then we analyze the existence of discrete almost automorphic solutions of linear and nonlinear difference equations in the scalar and in the abstract setting. Many questions remain open, as for example to prove the converse of (i) in Remark 2.2, that is, assuming that  is a discrete almost automorphic function, to find an almost automorphic function
is a discrete almost automorphic function, to find an almost automorphic function  such that
such that  for all
for all  (see [38, Theorem 1.27] in the almost periodic case). Concerning almost automorphic solutions of difference equations, it remains to study discrete almost automorphic solutions of Volterra difference equations as well as discrete almost automorphic solutions of functional difference equations with infinite delay. This topic should be handled by looking at the recent papers of Song [13, 14].
(see [38, Theorem 1.27] in the almost periodic case). Concerning almost automorphic solutions of difference equations, it remains to study discrete almost automorphic solutions of Volterra difference equations as well as discrete almost automorphic solutions of functional difference equations with infinite delay. This topic should be handled by looking at the recent papers of Song [13, 14].
References
Agarwal RP, Popenda J: Periodic solutions of first order linear difference equations. Mathematical and Computer Modelling 1995,22(1):11-19. 10.1016/0895-7177(95)00096-K
Corduneanu C: Almost periodic discrete processes. Libertas Mathematica 1982, 2: 159-169.
Halanay A: Solutions périodiques et presque-périodiques des systèmes d'équations aux différences finies. Archive for Rational Mechanics and Analysis 1963, 12: 134-149. 10.1007/BF00281222
Pang PYH, Agarwal RP: On periodicity of difference equations of a general type. Journal of Difference Equations and Applications 1996,2(3):271-287. 10.1080/10236199608808062
Sugiyama S: On periodic solutions of difference equations. Bulletin of Science and Engineering Research Laboratory. Waseda University 1971, 52: 89-94.
Elaydi S: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 3rd edition. Springer, New York, NY, USA; 2005:xxii+539.
Agarwal RP: Difference Equations and Inequalities, Monographs and Textbooks in Pure and Applied Mathematics. Volume 155. Marcel Dekker, New York, NY, USA; 1992:xiv+777.
Walther A: Fastperiodische Folgen und Potenzreihen mit fastperiodischen Koeffzienten. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1928, 6: 217-234. 10.1007/BF02940612
Walther A: Fastperiodische Folgen und ihre Fouriersche Analysis. Atti del Congresso Internazionale dei Matematici 1928, 2: 289-298.
Agarwal RP, O'Regan D, Wong PJY: Constant-sign periodic and almost periodic solutions of a system of difference equations. Computers & Mathematics with Applications 2005,50(10–12):1725-1754.
Hamaya Y: Existence of an almost periodic solution in a difference equation with infinite delay. Journal of Difference Equations and Applications 2003,9(2):227-237. 10.1080/1023619021000035836
Ignatyev AO, Ignatyev OA: On the stability in periodic and almost periodic difference systems. Journal of Mathematical Analysis and Applications 2006,313(2):678-688. 10.1016/j.jmaa.2005.04.001
Song Y: Almost periodic solutions of discrete Volterra equations. Journal of Mathematical Analysis and Applications 2006,314(1):174-194.
Song Y: Periodic and almost periodic solutions of functional difference equations with finite delay. Advances in Difference Equations 2007, 2007:-15.
Song Y, Tian H: Periodic and almost periodic solutions of nonlinear discrete Volterra equations with unbounded delay. Journal of Computational and Applied Mathematics 2007,205(2):859-870. 10.1016/j.cam.2005.12.042
Zhang S, Liu P, Gopalsamy K: Almost periodic solutions of nonautonomous linear difference equations. Applicable Analysis 2002,81(2):281-301. 10.1080/0003681021000021961
Minh NV, Naito T, Nguerekata G: A spectral countability condition for almost automorphy of solutions of differential equations. Proceedings of the American Mathematical Society 2006,134(11):3257-3266. 10.1090/S0002-9939-06-08528-5
Fatajou S, Minh NV, N'Guérékata GM, Pankov A: Stepanov-like almost automorphic solutions for nonautonomous evolution equations. Electronic Journal of Differential Equations 2007,2007(121):1-11.
Minh NV, Dat TT: On the almost automorphy of bounded solutions of differential equations with piecewise constant argument. Journal of Mathematical Analysis and Applications 2007,326(1):165-178. 10.1016/j.jmaa.2006.02.079
N'Guérékata GM: Topics in Almost Automorphy. Springer, New York, NY, USA; 2005:xii+168.
N'Guérékata GM: Almost Automorphic and Almost Periodic Functions in Abstract Spaces. Kluwer Academic/Plenum Publishers, New York, NY, USA; 2001:x+138.
Bochner S, von Neumann J: On compact solutions of operational-differential equations. I. Annals of Mathematics 1935,36(1):255-291. 10.2307/1968678
Bochner S: Uniform convergence of monotone sequences of functions. Proceedings of the National Academy of Sciences of the United States of America 1961, 47: 582-585. 10.1073/pnas.47.4.582
Bochner S: A new approach to almost periodicity. Proceedings of the National Academy of Sciences of the United States of America 1962, 48: 2039-2043. 10.1073/pnas.48.12.2039
Bochner S: Continuous mappings of almost automorphic and almost periodic functions. Proceedings of the National Academy of Sciences of the United States of America 1964, 52: 907-910. 10.1073/pnas.52.4.907
Araya D, Lizama C: Almost automorphic mild solutions to fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):3692-3705. 10.1016/j.na.2007.10.004
Goldstein JA, N'Guérékata GM: Almost automorphic solutions of semilinear evolution equations. Proceedings of the American Mathematical Society 2005,133(8):2401-2408. 10.1090/S0002-9939-05-07790-7
Zaidman S: Almost automorphic solutions of some abstract evolution equations. Istituto Lombardo, Accademia di Scienze e Lettere 1976,110(2):578-588.
Zaidman S:Behavior of trajectories of
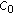 -semigroups. Istituto Lombardo, Accademia di Scienze e Lettere 1980, 114: 205-208.
-semigroups. Istituto Lombardo, Accademia di Scienze e Lettere 1980, 114: 205-208.Zaidman S: Existence of asymptotically almost-periodic and of almost-automorphic solutions for some classes of abstract differential equations. Annales des Sciences Mathématiques du Québec 1989,13(1):79-88.
Zaidman S: Topics in abstract differential equations. Nonlinear Analysis: Theory, Methods & Applications 1994,23(7):849-870. 10.1016/0362-546X(94)90124-4
Zaidman S: Topics in Abstract Differential Equations, Pitman Research Notes in Mathematics Series. Volume 304. Longman Scientific & Technical, Harlow, UK; 1994:xii+188.
Zaki M: Almost automorphic solutions of certain abstract differential equations. Annali di Matematica Pura ed Applicata 1974,101(1):91-114. 10.1007/BF02417100
Veech WA: Almost automorphic functions on groups. American Journal of Mathematics 1965, 87: 719-751. 10.2307/2373071
Gal SG, N'Guérékata GM: Almost automorphic fuzzy-number-valued functions. Journal of Fuzzy Mathematics 2005,13(1):185-208.
Gal CS, Gal SG, N'Guérékata GM: Almost automorphic functions in Fréchet spaces and applications to differential equations. Semigroup Forum 2005,71(2):201-230. 10.1007/s00233-005-0508-y
Gal CG, Gal SG, N'Guérékata GM:Almost automorphic functions with values in a
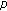 -Fréchet space. Electronic Journal of Differential Equations 2008, 21: 1-18.
-Fréchet space. Electronic Journal of Differential Equations 2008, 21: 1-18.Corduneanu C: Almost Periodic Functions, Interscience Tracts in Pure and Applied Mathematics, no. 2. John Wiley & Sons, New York, NY, USA; 1968:x+237.
Veech WA: Almost automorphic functions. Proceedings of the National Academy of Sciences of the United States of America 1963, 49: 462-464. 10.1073/pnas.49.4.462
Basit BR: A generalization of two theorems of M. I. Kadec on the indefinite integral of abstract almost periodic functions. Matematicheskie Zametki 1971, 9: 311-321.
Liu J, N'Guérékata GM, Minh NV: A Massera type theorem for almost automorphic solutions of differential equations. Journal of Mathematical Analysis and Applications 2004,299(2):587-599. 10.1016/j.jmaa.2004.05.046
Ezzinbi K, Nelson V, N'Guérékata GM:
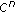 -almost automorphic solutions of some nonautonomous differential equations. Cubo 2008,10(2):61-74.
-almost automorphic solutions of some nonautonomous differential equations. Cubo 2008,10(2):61-74.
Acknowledgment
Carlos Lizama is partially supported by Laboratorio de Análisis Estocástico, Proyecto Anillo PBCT-ACT-13.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Araya, D., Castro, R. & Lizama, C. Almost Automorphic Solutions of Difference Equations. Adv Differ Equ 2009, 591380 (2009). https://doi.org/10.1155/2009/591380
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/591380
 is a continuous almost automorphic function in
is a continuous almost automorphic function in 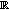 then
then  is discrete almost automorphic.
is discrete almost automorphic.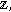 then we get discrete almost periodicity.
then we get discrete almost periodicity.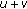 is discrete almost automorphic;
is discrete almost automorphic;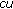 is discrete almost automorphic for every scalar
is discrete almost automorphic for every scalar  ;
; in
in  the function
the function 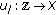 defined by
defined by  is discrete almost automorphic;
is discrete almost automorphic;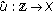 defined by
defined by 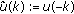 is discrete almost automorphic;
is discrete almost automorphic; ; that is,
; that is,  is a bounded function;
is a bounded function;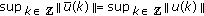 , where
, where
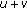 is discrete almost automorphic in
is discrete almost automorphic in 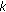 for each
for each  in
in 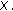
 is discrete almost automorphic in
is discrete almost automorphic in  for each
for each  in
in  where
where  is an arbitrary scalar.
is an arbitrary scalar. for each
for each  in
in  .
.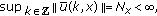 for each
for each  in
in  where
where  is the function in Definition 2.8.
is the function in Definition 2.8.
 such that
such that 
 in case
in case 
 in case
in case 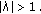
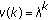 . Then
. Then  and hence, by Theorem 2.13, we obtain
and hence, by Theorem 2.13, we obtain  Next, we note that
Next, we note that  is solution of (3.2) because
is solution of (3.2) because 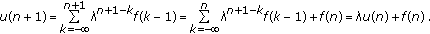
 and since
and since 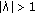 we have
we have 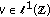 . It follows, by Theorem 2.13, that
. It follows, by Theorem 2.13, that 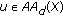 . Finally, we check that
. Finally, we check that  is solution of (3.2) as follows:
is solution of (3.2) as follows: 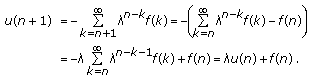
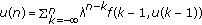 in case
in case  , and
, and in case
in case 
 -semigroups. Istituto Lombardo, Accademia di Scienze e Lettere 1980, 114: 205-208.
-semigroups. Istituto Lombardo, Accademia di Scienze e Lettere 1980, 114: 205-208.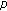 -Fréchet space. Electronic Journal of Differential Equations 2008, 21: 1-18.
-Fréchet space. Electronic Journal of Differential Equations 2008, 21: 1-18.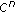 -almost automorphic solutions of some nonautonomous differential equations. Cubo 2008,10(2):61-74.
-almost automorphic solutions of some nonautonomous differential equations. Cubo 2008,10(2):61-74.