- Research Article
- Open access
- Published:
Existence of Solutions for 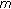 -point Boundary Value Problems on a Half-Line
-point Boundary Value Problems on a Half-Line
Advances in Difference Equations volume 2009, Article number: 609143 (2009)
Abstract
By using the Leray-Schauder continuation theorem, we establish the existence of solutions for  -point boundary value problems on a half-line
-point boundary value problems on a half-line 
 , where
, where  and
and  are given.
are given.
1. Introduction
Multipoint boundary value problems (BVPs) for second-order differential equations in a finite interval have been studied extensively and many results for the existence of solutions, positive solutions, multiple solutions are obtained by use of the Leray-Schauder continuation theorem, Guo-Krasnosel'skii fixed point theorem, and so on; for details see [1–4] and the references therein.
In the last several years, boundary value problems in an infinite interval have been arisen in many applications and received much attention; see [5, 6]. Due to the fact that an infinite interval is noncompact, the discussion about BVPs on the half-line is more complicated, see [5–14] and the references therein. Recently, in [15], Lian and Ge studied the following three-point boundary value problem:

where  and
and  are given. In this paper, we will study the following
are given. In this paper, we will study the following  -point boundary value problems:
-point boundary value problems:

where 
 have the same signal, and
have the same signal, and  are given. We first present the Green function for second-order multipoint BVPs on the half-line and then give the existence results for (1.2) using the properties of this Green function and the Leray-Schauder continuation theorem.
are given. We first present the Green function for second-order multipoint BVPs on the half-line and then give the existence results for (1.2) using the properties of this Green function and the Leray-Schauder continuation theorem.
We use the space  exists,
exists,  exists
exists with the norm
with the norm  , where
, where  is supremum norm on the half-line, and
is supremum norm on the half-line, and  is absolutely integrable on
is absolutely integrable on  with the norm
with the norm  .
.
We set

and we suppose  are the same signal in this paper and we always assume
are the same signal in this paper and we always assume 
2. Preliminary Results
In this section, we present some definitions and lemmas, which will be needed in the proof of the main results.
Definition 2.1 (see [15]).
It holds that  is called an S-Carathéodory function if and only if
is called an S-Carathéodory function if and only if
-
(i)
for each
 is measurable on
is measurable on 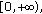
-
(ii)
for almost every
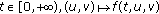 is continuous on
is continuous on  ,
, -
(iii)
for each
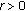 , there exists
, there exists 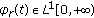 with
with  on
on 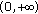 such that
such that  implies
implies 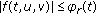 , for a.e.
, for a.e. 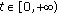 .
.
Lemma 2.2.
Suppose  if for any
if for any  with
with  , then the BVP,
, then the BVP,

has a unique solution. Moreover, this unique solution can be expressed in the form

where  is defined by
is defined by

here note 
Proof.
Integrate the differential equation from  to
to  , noticing that
, noticing that  , then from
, then from  to
to  and one has
and one has

Since  , from (2.4), it holds that
, from (2.4), it holds that

For  , the unique solution of (2.1) can be stated by
, the unique solution of (2.1) can be stated by

If  the unique solution of (2.1) can be stated by
the unique solution of (2.1) can be stated by

If  the unique solution of (2.1) can be stated by
the unique solution of (2.1) can be stated by

We note  then
then

Therefore, the unique solution of (2.1) is  which completes the proof.
which completes the proof.
Remark of Lemma 2.2 . Obviously  satisfies the properties of a Green function, so we call
satisfies the properties of a Green function, so we call  the Green function of the corresponding homogeneous multipoint BVP of (2.1) on the half-line.
the Green function of the corresponding homogeneous multipoint BVP of (2.1) on the half-line.
Lemma 2.3.
For all  , it holds that
, it holds that

Proof.
For each  ,
,  is nondecreasing in
is nondecreasing in  . Immediately, we have
. Immediately, we have

Further, we have

Therefore, we get the result.
Lemma 2.4.
For the Green function  , it holds that
, it holds that

Lemma 2.5.
For the function  it is satisfied that
it is satisfied that

and  have the same signal,
have the same signal,  , then there exists
, then there exists  satisfying
satisfying

where  .
.
Proof.
Let  are positive, and note
are positive, and note  , then for every
, then for every  , we have
, we have  so
so  that is,
that is,  Because
Because  is continuous on the interval
is continuous on the interval  , there exists
, there exists  satisfying
satisfying  , where
, where  .
.
Theorem 2.6 (see [5]).
Let  . Then
. Then  is relatively compact in
is relatively compact in  if the following conditions hold:
if the following conditions hold:
-
(a)
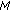 is uniformly bounded in
is uniformly bounded in  ;
; -
(b)
the functions from
 are equicontinuous on any compact interval of
are equicontinuous on any compact interval of 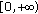 ;
; -
(c)
the functions from
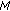 are equiconvergent, that is, for any given
are equiconvergent, that is, for any given  , there exists a
, there exists a  such that
such that 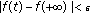 , for any
, for any  .
.
3. Main Results
Consider the space  and define the operator
and define the operator  by
by

The main result of this paper is following.
Theorem 3.1.
Let  be an S-Carathéodory function. Suppose further that there exists functions
be an S-Carathéodory function. Suppose further that there exists functions  with
with  such that
such that

for almost every  and all
and all  . Then (1.2) has at least one solution provided:
. Then (1.2) has at least one solution provided:

Lemma 3.2.
Let  be an S-Carathéodory function. Then, for each
be an S-Carathéodory function. Then, for each  is completely continuous in
is completely continuous in  .
.
Proof.
First we show  is well defined. Let
is well defined. Let  ; then there exists
; then there exists  such that
such that  . For each
. For each  , it holds that
, it holds that

Further,  is continuous in
is continuous in  so the Lebesgue dominated convergence theorem implies that
so the Lebesgue dominated convergence theorem implies that


where  . Thus,
. Thus,  .
.
Obviously,  . Notice that
. Notice that

so we can get  .
.
We claim that  is completely continuous in
is completely continuous in  , that is, for each
, that is, for each  ,
,  is continuous in
is continuous in  and maps a bounded subset of
and maps a bounded subset of  into a relatively compact set.
into a relatively compact set.
Let  as
as  in
in  . Next we prove that for each
. Next we prove that for each  ,
,  as
as  in
in  . Because
. Because  is a S-Carathéodory function and
is a S-Carathéodory function and

where  is a real number such that
is a real number such that  , we have
, we have

Also, we can get


Similarly, we have

For any positive number  , when
, when  , we have
, we have

Combining (3.9) (3.13), we can see that
(3.13), we can see that  is continuous. Let
is continuous. Let  be a bounded subset; it is easy to prove that
be a bounded subset; it is easy to prove that  is uniformly bounded. In the same way, we can prove (3.5),(3.6), and (3.12), we can also show that
is uniformly bounded. In the same way, we can prove (3.5),(3.6), and (3.12), we can also show that  is equicontinuous and equiconvergent. Thus, by Theorem 2.6,
is equicontinuous and equiconvergent. Thus, by Theorem 2.6,  is completely continuous. The proof is completed.
is completely continuous. The proof is completed.
Proof of Theorem 3.1.
In view of Lemma 2.2, it is clear that  is a solution of the BVP (1.2) if and only if
is a solution of the BVP (1.2) if and only if  is a fixed point of
is a fixed point of  Clearly,
Clearly,  for each
for each  If for each
If for each  the fixed points
the fixed points  in
in  belong to a closed ball of
belong to a closed ball of  independent of
independent of  then the Leray-Schauder continuation theorem completes the proof. We have known
then the Leray-Schauder continuation theorem completes the proof. We have known  is completely continuous by Lemma 3.2. Next we show that the fixed point of
is completely continuous by Lemma 3.2. Next we show that the fixed point of  has a priori bound
has a priori bound  independently of
independently of  . Assume
. Assume  and set
and set

According to Lemma 2.5, we know that for any  , there exists
, there exists  satisfying
satisfying  . Hence, there are three cases as follow.
. Hence, there are three cases as follow.
Case 1 ( ).
).
For any  holds and, therefore, there exists a
holds and, therefore, there exists a  such that
such that  . Then, we have
. Then, we have

and so it holds that

therefore,

At the same time, we have

and so

Set  , which is independent of
, which is independent of  .
.
Case 2 ( ).
).
For any  , we have
, we have

which implies that  for all
for all  . In the same way as for Case 1, we can get
. In the same way as for Case 1, we can get

Set  , which is independent of
, which is independent of  and is what we need.
and is what we need.
Case 3 ( ).
).
For  , we have
, we have

and so  for all
for all  .
.
Similarly, we obtain

Set  and which is we need. So (1.2) has at least one solution.
and which is we need. So (1.2) has at least one solution.
References
Gupta CP: A note on a second order three-point boundary value problem. Journal of Mathematical Analysis and Applications 1994,186(1):277-281. 10.1006/jmaa.1994.1299
Gupta CP, Trofimchuk SI: A sharper condition for the solvability of a three-point second order boundary value problem. Journal of Mathematical Analysis and Applications 1997,205(2):586-597. 10.1006/jmaa.1997.5252
Ma R: Positive solutions for second-order three-point boundary value problems. Applied Mathematics Letters 2001,14(1):1-5. 10.1016/S0893-9659(00)00102-6
Guo Y, Ge W: Positive solutions for three-point boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2004,290(1):291-301. 10.1016/j.jmaa.2003.09.061
O'Regan D: Theory of Singular Boundary Value Problems. World Scientific, River Edge, NJ, USA; 1994:xii+154.
Agarwal RP, O'Regan D: Infinite Interval Problems for Differential, Difference and Integral Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+341.
Baxley JV: Existence and uniqueness for nonlinear boundary value problems on infinite intervals. Journal of Mathematical Analysis and Applications 1990,147(1):122-133. 10.1016/0022-247X(90)90388-V
Jiang D, Agarwal RP:A uniqueness and existence theorem for a singular third-order boundary value problem on
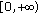 . Applied Mathematics Letters 2002,15(4):445-451. 10.1016/S0893-9659(01)00157-4
. Applied Mathematics Letters 2002,15(4):445-451. 10.1016/S0893-9659(01)00157-4Ma R: Existence of positive solution for second-order boundary value problems on infinite intervals. Applied Mathematics Letters 2003, 16: 33-39. 10.1016/S0893-9659(02)00141-6
Bai C, Fang J: On positive solutions of boundary value problems for second-order functional differential equations on infinite intervals. Journal of Mathematical Analysis and Applications 2003,282(2):711-731. 10.1016/S0022-247X(03)00246-4
Yan B, Liu Y: Unbounded solutions of the singular boundary value problems for second order differential equations on the half-line. Applied Mathematics and Computation 2004,147(3):629-644. 10.1016/S0096-3003(02)00801-9
Tian Y, Ge W: Positive solutions for multi-point boundary value problem on the half-line. Journal of Mathematical Analysis and Applications 2007,325(2):1339-1349. 10.1016/j.jmaa.2006.02.075
Tian Y, Ge W, Shan W: Positive solutions for three-point boundary value problem on the half-line. Computers & Mathematics with Applications 2007,53(7):1029-1039.
Zima M: On positive solutions of boundary value problems on the half-line. Journal of Mathematical Analysis and Applications 2001,259(1):127-136. 10.1006/jmaa.2000.7399
Lian H, Ge W: Solvability for second-order three-point boundary value problems on a half-line. Applied Mathematics Letters 2006,19(10):1000-1006. 10.1016/j.aml.2005.10.018
Acknowledgment
The Natural Science Foundation of Hebei Province (A2009000664) and the Foundation of Hebei University of Science and Technology (XL200759) are acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, C., Guo, Y. & Ji, Y. Existence of Solutions for 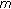 -point Boundary Value Problems on a Half-Line.
Adv Differ Equ 2009, 609143 (2009). https://doi.org/10.1155/2009/609143
-point Boundary Value Problems on a Half-Line.
Adv Differ Equ 2009, 609143 (2009). https://doi.org/10.1155/2009/609143
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/609143
 is measurable on
is measurable on 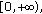
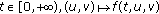 is continuous on
is continuous on  ,
,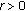 , there exists
, there exists 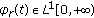 with
with  on
on 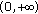 such that
such that  implies
implies 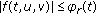 , for a.e.
, for a.e. 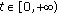 .
.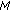 is uniformly bounded in
is uniformly bounded in  ;
; are equicontinuous on any compact interval of
are equicontinuous on any compact interval of 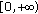 ;
;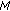 are equiconvergent, that is, for any given
are equiconvergent, that is, for any given  , there exists a
, there exists a  such that
such that 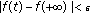 , for any
, for any  .
. . Applied Mathematics Letters 2002,15(4):445-451. 10.1016/S0893-9659(01)00157-4
. Applied Mathematics Letters 2002,15(4):445-451. 10.1016/S0893-9659(01)00157-4