- Research Article
- Open access
- Published:
Solution and Stability of a Mixed Type Additive, Quadratic, and Cubic Functional Equation
Advances in Difference Equations volume 2009, Article number: 826130 (2009)
Abstract
We obtain the general solution and the generalized Hyers-Ulam-Rassias stability of the mixed type additive, quadratic, and cubic functional equation  .
.
1. Introduction
The stability problem of functional equations originated from a question of Ulam [1] in 1940, concerning the stability of group homomorphisms. Let  be a group, and let
be a group, and let  be a metric group with the metric
be a metric group with the metric  Given
Given  , does there exist a
, does there exist a  , such that if a mapping
, such that if a mapping  satisfies the inequality
satisfies the inequality  for all
for all  , then there exists a homomorphism
, then there exists a homomorphism  with
with  for all
for all  ? In other words, under what condition does there exist a homomorphism near an approximate homomorphism?
? In other words, under what condition does there exist a homomorphism near an approximate homomorphism?
In 1941, Hyers [2] gave a first affirmative answer to the question of Ulam for Banach spaces. Let  be a mapping between Banach spaces such that
be a mapping between Banach spaces such that

for all  and for some
and for some  Then there exists a unique additive mapping
Then there exists a unique additive mapping  such that
such that

for all  Moreover if
Moreover if  is continuous in
is continuous in  for each fixed
for each fixed  then
then  is linear (see also [3]). In 1950, Aoki [4] generalized Hyers' theorem for approximately additive mappings. In 1978, Th. M. Rassias [5] provided a generalization of Hyers' theorem which allows the Cauchy difference to be unbounded. This new concept is known as Hyers-Ulam-Rassias stability of functional equations (see [2–24]).
is linear (see also [3]). In 1950, Aoki [4] generalized Hyers' theorem for approximately additive mappings. In 1978, Th. M. Rassias [5] provided a generalization of Hyers' theorem which allows the Cauchy difference to be unbounded. This new concept is known as Hyers-Ulam-Rassias stability of functional equations (see [2–24]).
The functional equation

is related to symmetric biadditive function. In the real case it has  among its solutions. Thus, it has been called quadratic functional equation, and each of its solutions is said to be a quadratic function. Hyers-Ulam-Rassias stability for the quadratic functional equation (1.3) was proved by Skof for functions
among its solutions. Thus, it has been called quadratic functional equation, and each of its solutions is said to be a quadratic function. Hyers-Ulam-Rassias stability for the quadratic functional equation (1.3) was proved by Skof for functions  , where
, where  is normed space and
is normed space and  Banach space (see [25–28]).
Banach space (see [25–28]).
The following cubic functional equation was introduced by the third author of this paper, J. M. Rassias [29, 30] (in 2000-2001):

Jun and Kim [13] introduced the following cubic functional equation:

and they established the general solution and the generalized Hyers-Ulam-Rassias stability for the functional equation (1.5).
The function  satisfies the functional equation (1.5), which explains why it is called cubic functional equation.
satisfies the functional equation (1.5), which explains why it is called cubic functional equation.
Jun and Kim proved that a function  between real vector spaces
between real vector spaces  and
and  is a solution of (1.5) if and only if there exists a unique function
is a solution of (1.5) if and only if there exists a unique function  such that
such that  for all
for all  and
and  is symmetric for each fixed one variable and is additive for fixed two variables (see also [31–33]).
is symmetric for each fixed one variable and is additive for fixed two variables (see also [31–33]).
We deal with the following functional equation deriving from additive, cubic and quadratic functions:

It is easy to see that the function  is a solution of the functional equation (1.6). In the present paper we investigate the general solution and the generalized Hyers-Ulam-Rassias stability of the functional equation (1.6).
is a solution of the functional equation (1.6). In the present paper we investigate the general solution and the generalized Hyers-Ulam-Rassias stability of the functional equation (1.6).
2. General Solution
In this section we establish the general solution of functional equation (1.6).
Theorem 2.1.
Let  ,
, be vector spaces, and let
be vector spaces, and let  be a function. Then
be a function. Then  satisfies (1.6) if and only if there exists a unique additive function
satisfies (1.6) if and only if there exists a unique additive function  , a unique symmetric and biadditive function
, a unique symmetric and biadditive function  and a unique symmetric and 3-additive function
and a unique symmetric and 3-additive function  such that
such that  for all
for all  .
.
Proof.
Suppose that  for all
for all  , where
, where  is additive,
is additive,  is symmetric and biadditive, and
is symmetric and biadditive, and  is symmetric and 3-additive. Then it is easy to see that
is symmetric and 3-additive. Then it is easy to see that  satisfies (1.6). For the converse let
satisfies (1.6). For the converse let  satisfy (1.6). We decompose
satisfy (1.6). We decompose  into the even part and odd part by setting
into the even part and odd part by setting

for all  By (1.6), we have
By (1.6), we have

for all  This means that
This means that  satisfies (1.6), that is,
satisfies (1.6), that is,

Now putting  in (2.3), we get
in (2.3), we get  . Setting
. Setting  in (2.3), by evenness of
in (2.3), by evenness of  we obtain
we obtain

Replacing  by
by  in (2.3), we obtain
in (2.3), we obtain

Comparing (2.4) with (2.5), we get

By utilizing (2.5) with (2.6), we obtain

Hence, according to (2.6) and (2.7), (2.3) can be written as

With the substitution  in (2.8), we have
in (2.8), we have

Replacing  by
by  in above relation, we obtain
in above relation, we obtain

Setting  instead of
instead of  in (2.8), we get
in (2.8), we get

Interchanging  and
and  in (2.11), we get
in (2.11), we get

If we subtract (2.12) from (2.11) and use (2.10), we obtain

which, by putting  and using (2.7), leads to
and using (2.7), leads to

Let us interchange  and
and  in (2.14). Then we see that
in (2.14). Then we see that

and by adding (2.14) and (2.15), we arrive at

Replacing  by
by  in (2.8), we obtain
in (2.8), we obtain

Let us Interchange  and
and  in (2.17). Then we see that
in (2.17). Then we see that

Thus by adding (2.17) and (2.18), we have

Replacing  by
by  in (2.11) and using (2.7) we have
in (2.11) and using (2.7) we have

and interchanging  and
and  in (2.20) yields
in (2.20) yields

If we add (2.20) to (2.21), we have

Interchanging  and
and  in (2.8), we get
in (2.8), we get

and by adding the last equation and (2.8) with (2.19), we get

Now according to (2.22) and (2.24), it follows that

From the substitution  in (2.25) it follows that
in (2.25) it follows that

Replacing  by
by  in (2.25) we have
in (2.25) we have

and interchanging  and
and  yields
yields

By adding (2.27) and (2.28) and then using (2.25) and (2.26), we lead to

If we compare (2.16) and (2.29), we conclude that

This means that  is quadratic. Thus there exists a unique quadratic function
is quadratic. Thus there exists a unique quadratic function  such that
such that  for all
for all  On the other hand we can show that
On the other hand we can show that  satisfies (1.6), that is,
satisfies (1.6), that is,

Now we show that the mapping  defined by
defined by  is additive and the mapping
is additive and the mapping  defined by
defined by  is cubic. Putting
is cubic. Putting  in (2.31), then by oddness of
in (2.31), then by oddness of  we have
we have

Hence (2.31) can be written as

From the substitution  in (2.33) it follows that
in (2.33) it follows that

Interchange  and
and  in (2.33), and it follows that
in (2.33), and it follows that

With the substitutions  and
and  in (2.35), we have
in (2.35), we have

Replace  by
by  in (2.34). Then we have
in (2.34). Then we have

Replacing  by
by  in (2.37) gives
in (2.37) gives

Interchanging  and
and  in (2.38), we get
in (2.38), we get

If we add (2.38) to (2.39), we have

Replacing  by
by  in (2.36) gives
in (2.36) gives

By comparing (2.40) with (2.41), we arrive at

Replacing  by
by  in (2.42) gives
in (2.42) gives

With the substitution  in (2.43), we have
in (2.43), we have

and replacing  by
by  gives
gives

Let us interchange  and
and  in (2.45). Then we see that
in (2.45). Then we see that

If we add (2.45) to (2.46), we have

Adding (2.42) to (2.47) and using (2.33) and (2.35), we obtain

for all  The last equality means that
The last equality means that

for all  Therefore the mapping
Therefore the mapping  is additive. With the substitutions
is additive. With the substitutions  and
and  in (2.35), we have
in (2.35), we have

Let  be the additive mapping defined above. It is easy to show that
be the additive mapping defined above. It is easy to show that  is cubic-additive function. Then there exists a unique function
is cubic-additive function. Then there exists a unique function  and a unique additive function
and a unique additive function  such that
such that  for all
for all  and
and  is symmetric and 3-additive. Thus for all
is symmetric and 3-additive. Thus for all  , we have
, we have

This completes the proof of theorem.
The following corollary is an alternative result of Theorem 2.1.
Corollary 2.2.
Let  ,
, be vector spaces, and let
be vector spaces, and let  be a function satisfying (1.6). Then the following assertions hold.
be a function satisfying (1.6). Then the following assertions hold.
-
(a)
If
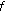 is even function, then
is even function, then 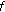 is quadratic.
is quadratic. -
(b)
If
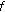 is odd function, then
is odd function, then 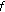 is cubic-additive.
is cubic-additive.
3. Stability
We now investigate the generalized Hyers-Ulam-Rassias stability problem for functional equation (1.6). From now on, let  be a real vector space, and let
be a real vector space, and let  be a Banach space. Now before taking up the main subject, given
be a Banach space. Now before taking up the main subject, given  , we define the difference operator
, we define the difference operator  by
by

for all  We consider the following functional inequality:
We consider the following functional inequality:

for an upper bound 
Theorem 3.1.
Let  be fixed. Suppose that an even mapping
be fixed. Suppose that an even mapping  satisfies
satisfies  and
and

for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that

for all  then the limit
then the limit

exists for all  and
and  is a unique quadratic function satisfying (1.6), and
is a unique quadratic function satisfying (1.6), and

for all 
Proof.
Let  Putting
Putting  in (3.3), we get
in (3.3), we get

for all  On the other hand by replacing
On the other hand by replacing  by
by  in (3.3), it follows that
in (3.3), it follows that

for all  Combining (3.8) and (3.9), we lead to
Combining (3.8) and (3.9), we lead to

for all  With the substitution
With the substitution  in (3.10) and then dividing both sides of inequality by 2, we get
in (3.10) and then dividing both sides of inequality by 2, we get

Now, using methods similar as in [8, 34, 35], we can easily show that the function  defined by
defined by  for all
for all  is unique quadratic function satisfying (1.6) and (3.7). Let
is unique quadratic function satisfying (1.6) and (3.7). Let  Then by (3.10) we have
Then by (3.10) we have

for all  And analogously, as in the case
And analogously, as in the case  , we can show that the function
, we can show that the function  defined by
defined by  is unique quadratic function satisfying (1.6) and (3.7).
is unique quadratic function satisfying (1.6) and (3.7).
Theorem 3.2.
Let  be fixed. Let
be fixed. Let  is a mapping such that
is a mapping such that

and that

for all 
Suppose that an odd mapping  satisfies
satisfies

for all 
Then the limit

exists, for all  and
and  is a unique additive function satisfying (1.6), and
is a unique additive function satisfying (1.6), and

for all 
Proof.
Let  set
set  in (3.15). Then by oddness of
in (3.15). Then by oddness of  we have
we have

for all  Replacing
Replacing  by
by  in (3.15) we get
in (3.15) we get

Combining (3.18) and (3.19), we lead to

for all  Putting
Putting  and
and  for all
for all  Then we get
Then we get

for all  Now, in a similar way as in [8, 34, 35], we can show that the limit
Now, in a similar way as in [8, 34, 35], we can show that the limit  exists, for all
exists, for all  and
and  is the unique function satisfying (1.6) and (3.17). If
is the unique function satisfying (1.6) and (3.17). If  , then the proof is analogous.
, then the proof is analogous.
Theorem 3.3.
Let  be fixed. Suppose that an odd mapping
be fixed. Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that  for all
for all  then the limit
then the limit

exists, for all  and
and  is a unique cubic function satisfying (1.6) and
is a unique cubic function satisfying (1.6) and

for all 
Proof.
We prove the theorem for  When
When  we have a similar proof. It is easy to see that
we have a similar proof. It is easy to see that  satisfies (3.20). Set
satisfies (3.20). Set  then by putting
then by putting  in (3.20), it follows that
in (3.20), it follows that

for all  By using (3.26), we may define a mapping
By using (3.26), we may define a mapping  as
as  for all
for all  Similar to Theorem 3.1, we can show that
Similar to Theorem 3.1, we can show that  is the unique cubic function satisfying (1.6) and (3.25).
is the unique cubic function satisfying (1.6) and (3.25).
Theorem 3.4.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that  for all
for all  then there exists a unique cubic function
then there exists a unique cubic function  and a unique additive function
and a unique additive function  such that
such that

for all 
Proof.
By Theorems 3.2 and 3.3, there exist an additive mapping  and a cubic mapping
and a cubic mapping  such that
such that

for all  Combine the two equations of (3.30) to obtain
Combine the two equations of (3.30) to obtain

for all  So we get (3.29) by letting
So we get (3.29) by letting  and
and  for all
for all  To prove the uniqueness of
To prove the uniqueness of  and
and  let
let  be another additive and cubic maps satisfying (3.29). Let
be another additive and cubic maps satisfying (3.29). Let  , and let
, and let  So
So

for all  Since
Since

then

for all  Hence (3.32) implies that
Hence (3.32) implies that

for all  On the other hand
On the other hand  and
and  are cubic, then
are cubic, then  Therefore by (3.35) we obtain that
Therefore by (3.35) we obtain that  for all
for all  Again by (3.35) we have
Again by (3.35) we have  for all
for all 
Theorem 3.5.
Suppose that an odd mapping  satisfies
satisfies

for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that  for all
for all  then there exist a unique cubic function
then there exist a unique cubic function  and a unique additive function
and a unique additive function  such that
such that

for all 
Proof.
The proof is similar to the proof of Theorem 3.4.
Now we establish the generalized Hyers-Ulam-Rassias stability of functional equation (1.6) as follows.
Theorem 3.6.
Suppose that a mapping  satisfies
satisfies  and
and  for all
for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that  for all
for all  then there exist a unique additive function
then there exist a unique additive function  a unique quadratic function
a unique quadratic function  and a unique cubic function
and a unique cubic function  such that
such that

for all  .
.
Proof.
Let  for all
for all  Then
Then  and
and  for all
for all  Hence in view of Theorem 3.1 there exists a unique quadratic function
Hence in view of Theorem 3.1 there exists a unique quadratic function  satisfying (3.7). Let
satisfying (3.7). Let  for all
for all  Then
Then  and
and  for all
for all  From Theorem 3.4, it follows that there exist a unique cubic function
From Theorem 3.4, it follows that there exist a unique cubic function  and a unique additive function
and a unique additive function  satisfying (3.29). Now it is obvious that (3.40) holds true for all
satisfying (3.29). Now it is obvious that (3.40) holds true for all  and the proof of theorem is complete.
and the proof of theorem is complete.
Corollary 3.7.
Let  Suppose that a mapping
Suppose that a mapping  satisfies
satisfies  and
and

for all  Then there exist a unique additive function
Then there exist a unique additive function  a unique quadratic function
a unique quadratic function  and a unique cubic function
and a unique cubic function  satisfying
satisfying

for all 
Proof.
It follows from Theorem 3.6 by taking  for all
for all  .
.
Theorem 3.8.
Suppose that  satisfies
satisfies  and
and  for all
for all  If the upper bound
If the upper bound  is a mapping such that
is a mapping such that

and that  for all
for all  then there exists a unique additive function
then there exists a unique additive function  a unique quadratic function
a unique quadratic function  and a unique cubic function
and a unique cubic function  such that
such that

for all  .
.
By Theorem 3.8, we are going to investigate the following stability problem for functional equation (1.6).
Corollary 3.9.
Let  Suppose that
Suppose that  satisfies
satisfies  and
and

for all  then there exist a unique additive function
then there exist a unique additive function  a unique quadratic function
a unique quadratic function  and a unique cubic function
and a unique cubic function  satisfying
satisfying

for all  .
.
By Corollary 3.9, we solve the following Hyers-Ulam stability problem for functional equation (1.6).
Corollary 3.10.
Let  be a positive real number. Suppose that a mapping
be a positive real number. Suppose that a mapping  satisfies
satisfies  and
and  for all
for all  then there exist a unique additive function
then there exist a unique additive function  a unique quadratic function
a unique quadratic function  and a unique cubic function
and a unique cubic function  such that
such that

for all  .
.
References
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1940.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and Their Applications, 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223-237. 10.1090/S0002-9904-1951-09511-7
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64-66. 10.2969/jmsj/00210064
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297-300. 10.1090/S0002-9939-1978-0507327-1
Aczél J, Dhombres J: Functional Equations in Several Variables, Encyclopedia of Mathematics and Its Applications. Volume 31. Cambridge University Press, Cambridge, UK; 1989:xiv+462.
Cholewa PW: Remarks on the stability of functional equations. Aequationes Mathematicae 1984,27(1-2):76-86.
Forti G-L: Comments on the core of the direct method for proving Hyers-Ulam stability of functional equations. Journal of Mathematical Analysis and Applications 2004,295(1):127-133. 10.1016/j.jmaa.2004.03.011
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991,14(3):431-434. 10.1155/S016117129100056X
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431-436. 10.1006/jmaa.1994.1211
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222-224. 10.1073/pnas.27.4.222
Isac G, Rassias ThM:On the Hyers-Ulam stability of
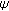 -additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010Jun K-W, Kim H-M: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. Journal of Mathematical Analysis and Applications 2002,274(2):267-278.
Maligranda L: A result of Tosio Aoki about a generalization of Hyers-Ulam stability of additive functions—a question of priority. Aequationes Mathematicae 2008,75(3):289-296. 10.1007/s00010-007-2892-8
Rassias JM: On a new approximation of approximately linear mappings by linear mappings. Discussiones Mathematicae 1985, 7: 193-196.
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques. Deuxième Série 1984,108(4):445-446.
Rassias JM: Complete solution of the multi-dimensional problem of Ulam. Discussiones Mathematicae 1994, 14: 101-107.
Rassias JM: On the stability of a multi-dimensional Cauchy type functional equation. In Geometry, Analysis and Mechanics. World Scientific, River Edge, NJ, USA; 1994:365-376.
Rassias JM: Solution of a stability problem of Ulam. In Functional Analysis, Approximation Theory and Numerical Analysis. World Scientific, River Edge, NJ, USA; 1994:241-249.
Rassias JM: Solution of a stability problem of Ulam. Discussiones Mathematicae 1992, 12: 95-103.
Rassias JM: Solution of a problem of Ulam. Journal of Approximation Theory 1989,57(3):268-273. 10.1016/0021-9045(89)90041-5
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982,46(1):126-130. 10.1016/0022-1236(82)90048-9
Rassias ThM (Ed): Functional Equations and Inequalities, Mathematics and Its Applications. Volume 518. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xii+336.
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264-284. 10.1006/jmaa.2000.7046
Grabiec A: The generalized Hyers-Ulam stability of a class of functional equations. Publicationes Mathematicae Debrecen 1996,48(3-4):217-235.
Rassias JM, Rassias MJ: Refined Ulam stability for Euler-Lagrange type mappings in Hilbert spaces. International Journal of Applied Mathematics & Statistics 2007, 7: 126-132.
Rassias JM: On the stability of the Euler-Lagrange functional equation. Chinese Journal of Mathematics 1992,20(2):185-190.
Skof F: Proprieta' locali e approssimazione di operatori. Rendiconti del Seminario Matematico e Fisico di Milano 1983, 53: 113-129. 10.1007/BF02924890
Rassias JM: Solution of the Ulam stability problem for cubic mappings. Glasnik Matematički. Serija III 2001,36(56)(1):63-72.
Rassias JM: Solution of the Ulam problem for cubic mappings. Analele Universităţii din Timişoara. Seria Matematică-Informatică 2000,38(1):121-132.
Gordji ME: Stability of a functional equation deriving from quartic and additive functions. to appear in Bulletin of the Korean Mathematical Society
Gordji ME, Ebadian A, Zolfaghari S: Stability of a functional equation deriving from cubic and quartic functions. Abstract and Applied Analysis 2008, 2008:-17.
Gordji ME, Khodaei H: Solution and stability of generalized mixed type cubic, quadratic and additive functional equation in quasi-Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009, 71: 5629-5643. 10.1016/j.na.2009.04.052
Brzdęk J, Pietrzyk A: A note on stability of the general linear equation. Aequationes Mathematicae 2008,75(3):267-270. 10.1007/s00010-007-2894-6
Pietrzyk A: Stability of the Euler-Lagrange-Rassias functional equation. Demonstratio Mathematica 2006,39(3):523-530.
Acknowledgments
The authors would like to express their sincere thanks to referees for their invaluable comments. The first author would like to thank the Semnan University for its financial support. Also, the fourth author would like to thank the office of gifted students at Semnan University for its financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Eshaghi Gordji, M., Kaboli Gharetapeh, S., Rassias, J.M. et al. Solution and Stability of a Mixed Type Additive, Quadratic, and Cubic Functional Equation. Adv Differ Equ 2009, 826130 (2009). https://doi.org/10.1155/2009/826130
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/826130
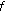 is even function, then
is even function, then 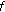 is quadratic.
is quadratic.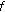 is odd function, then
is odd function, then 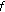 is cubic-additive.
is cubic-additive.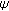 -additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010
-additive mappings. Journal of Approximation Theory 1993,72(2):131-137. 10.1006/jath.1993.1010