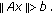- Research Article
- Open access
- Published:
Multiple Positive Solutions for Nonlinear First-Order Impulsive Dynamic Equations on Time Scales with Parameter
Advances in Difference Equations volume 2009, Article number: 830247 (2009)
Abstract
By using the Leggett-Williams fixed point theorem, the existence of three positive solutions to a class of nonlinear first-order periodic boundary value problems of impulsive dynamic equations on time scales with parameter are obtained. An example is given to illustrate the main results in this paper.
1. Introduction
Let  be a time scale, that is,
be a time scale, that is,  is a nonempty closed subset of
is a nonempty closed subset of  . Let
. Let  be fixed and
be fixed and  be points in
be points in  , an interval
, an interval  denoting time scales interval, that is,
denoting time scales interval, that is,  Other types of intervals are defined similarly. Some definitions concerning time scales can be found in [1–5].
Other types of intervals are defined similarly. Some definitions concerning time scales can be found in [1–5].
In this paper, we are concerned with the existence of positive solutions for the following nonlinear first-order periodic boundary value problem on time scales:

where  is a positive parameter,
is a positive parameter,  ,
,  is right-dense continuous,
is right-dense continuous,  ,
,  and for each
and for each  and
and  represent the right and left limits of
represent the right and left limits of  at
at  .
.
The theory of impulsive differential equations is emerging as an important area of investigation, since it is a lot richer than the corresponding theory of differential equations without impulse effects. Moreover, such equations may exhibit several real world phenomena in physics, biology, engineering, and so forth, (see [6–8]). At the same time, the boundary value problems for impulsive differential equations and impulsive difference equations have received much attention [9–19]. On the other hand, recently, the theory of dynamic equations on time scales has become a new important branch (see, e.g., [1–5]). Naturally, some authors have focused their attention on the boundary value problems of impulsive dynamic equations on time scales [20–27]. In particular, for the first-order impulsive dynamic equations on time scales

where  is a time scale which has at least finitely-many right-dense points,
is a time scale which has at least finitely-many right-dense points,  is regressive and right-dense continuous,
is regressive and right-dense continuous,  is given function,
is given function,  . The paper [21] obtained the existence of one solution to problem (1.2) by using the nonlinear alternative of Leray-Schauder type.
. The paper [21] obtained the existence of one solution to problem (1.2) by using the nonlinear alternative of Leray-Schauder type.
In [22], Benchohra et al. considered the following impulsive boundary value problem on time scales

They proved the existence of one solution to the problem (1.3) by applying Schaefer's fixed point theorem and the nonlinear alternative of Leray-Schauder type.
In [26], Li and Shen studied the problem (1.3). Some existence results to problem (1.3) are established by using a fixed point theorem, which is due to Krasnoselskii and Zabreiko, and the Leggett-Williams fixed point theorem.
In [27], the first author studied the problem (1.1) when  . The existence of positive solutions to the problem (1.1) was obtained by means of the well-known Guo-Krasnoselskii fixed point theorem.
. The existence of positive solutions to the problem (1.1) was obtained by means of the well-known Guo-Krasnoselskii fixed point theorem.
Recently, Sun and Li [28] considered the following periodic boundary value problem:

By using the fixed point index, some existence, multiplicity and nonexistence criteria of positive solutions to the problem (1.4) were obtained for suitable  .
.
Motivated by the results mentioned above, in this paper, we shall show that the problem (1.1) has at least three positive solutions for suitable  by using the Leggett-Williams fixed point theorem [29]. We note that for the case
by using the Leggett-Williams fixed point theorem [29]. We note that for the case  and
and  problem (1.1) reduces to the problem studied by [30].
problem (1.1) reduces to the problem studied by [30].
In the remainder of this section, we state the following theorem, which are crucial to our proof.
Let  be a real Banach space and
be a real Banach space and  be a cone. A function
be a cone. A function  is called a nonnegative continuous concave functional if
is called a nonnegative continuous concave functional if  is continuous and
is continuous and

for all  and
and  .
.
Let  be constants,
be constants, 
Theorem 1.1 (see [29]).
Let  be a completely continuous map and
be a completely continuous map and  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  such that
such that  Suppose there exist
Suppose there exist  with
with  such that
such that
-
(i)
 and
and 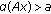
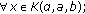
-
(ii)


-
(iii)

 with
with 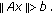
Then  has at least three fixed points
has at least three fixed points  in
in  satisfying
satisfying

2. Preliminaries
Throughout the rest of this paper, we always assume that the points of impulse  are right-dense for each
are right-dense for each 
We define

where  is the restriction of
is the restriction of  to
to  and
and 
Let

with the norm  Then X is a Banach space.
Then X is a Banach space.
Definition 2.1.
A function  is said to be a solution of the problem (1.1) if and only if
is said to be a solution of the problem (1.1) if and only if  satisfies the dynamic equation
satisfies the dynamic equation

the impulsive conditions

and the periodic boundary condition 
Lemma 2.2.
Suppose  is
is  -continuous, then
-continuous, then  is a solution of
is a solution of

where

if and only if  is a solution of the boundary value problem
is a solution of the boundary value problem

Proof.
Since the method is similar to that of in [27, Lemma 3.1], we omit it here.
Lemma 2.3.
Let  be defined as Lemma 2.2, then
be defined as Lemma 2.2, then

Proof.
It is obvious, so we omit it here.
Let

where  It is not difficult to verify that
It is not difficult to verify that  is a cone in
is a cone in 
We define an operator  by
by

By [27, Lemmas 3.3 and 3.4], it is easy to see that  is completely continuous.
is completely continuous.
3. Main Result
Notation 1.
Let

and for  we define
we define 
Theorem 3.1.
Assume that there exists a number  such that the following conditions:
such that the following conditions:
(H1) for
for 
(H2) hold. Then the problem (1.1) has at least three positive solutions for
hold. Then the problem (1.1) has at least three positive solutions for

Proof.
Let  it is easy to see that
it is easy to see that  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  such that
such that 
First, we assert that there exists  such that
such that  is completely continuous.
is completely continuous.
In fact, by the condition  of (H2), there exist
of (H2), there exist  and
and  such that
such that

Let  if
if  then
then  and we have
and we have

Take  then the set
then the set  is a bounded set. According to that
is a bounded set. According to that  is completely continuous, then
is completely continuous, then  maps bounded sets into bounded sets and there exists a number
maps bounded sets into bounded sets and there exists a number  such that
such that

If  we deduce that
we deduce that  is completely continuous. If
is completely continuous. If  then from (3.4), we know that for any
then from (3.4), we know that for any  and
and  hold. Then we have
hold. Then we have  is completely continuous. Take
is completely continuous. Take  then
then  and
and  are completely continuous.
are completely continuous.
Second, we assert that  and
and  for all
for all 
In fact, take  so
so  Moreover, for
Moreover, for  then
then  and we have
and we have

Third, we assert that there exist  such that
such that  if
if 
Indeed, by the condition  of (H2), there exist
of (H2), there exist  and
and  such that
such that

Then  we get
we get

Finally, we assert that  if
if  and
and 
To do this, if  and
and  then
then

To sum up, all the hypotheses of Theorem 1.1 are satisfied by taking  Hence
Hence  has at least three fixed points, that is, the problem (1.1) has at least three positive solutions
has at least three fixed points, that is, the problem (1.1) has at least three positive solutions  and
and  such that
such that

Corollary 3.2.
Using (H3)  instead of (H2) in Theorem 3.1, the conclusion of Theorem 3.1 remains true.
instead of (H2) in Theorem 3.1, the conclusion of Theorem 3.1 remains true.
4. Example
Example 4.1.
Let  We consider the following problem on
We consider the following problem on 

where  is a positive parameter,
is a positive parameter,  and
and

Taking  then by
then by  it is easy to see that
it is easy to see that  So, for all
So, for all  we have
we have  Obviously, we have
Obviously, we have 
Therefore, together with Corollary 3.2, it follows that the problem (4.1) has at least three positive solutions for  .
.
References
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Hilger S: Analysis on measure chains-a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Baĭnov DD, Simeonov PS: Systems with Impulse Effect: Stability, Theory and Applications, Ellis Horwood Series: Mathematics and Its Applications. Ellis Horwood, Chichester, UK; 1989:255.
Bainov DD, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, Harlow, UK; 1993.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Agarwal RP, O'Regan D: Multiple nonnegative solutions for second order impulsive differential equations. Applied Mathematics and Computation 2000,114(1):51-59. 10.1016/S0096-3003(99)00074-0
He Z, Yu J: Periodic boundary value problem for first-order impulsive functional differential equations. Journal of Computational and Applied Mathematics 2002,138(2):205-217. 10.1016/S0377-0427(01)00381-8
He Z, Zhang X: Monotone iterative technique for first order impulsive difference equations with periodic boundary conditions. Applied Mathematics and Computation 2004,156(3):605-620. 10.1016/j.amc.2003.08.013
Li J-L, Shen J-H: Existence of positive periodic solutions to a class of functional differential equations with impulses. Mathematica Applicata 2004,17(3):456-463.
Li J, Nieto JJ, Shen J: Impulsive periodic boundary value problems of first-order differential equations. Journal of Mathematical Analysis and Applications 2007,325(1):226-236. 10.1016/j.jmaa.2005.04.005
Li J, Shen J: Positive solutions for first order difference equations with impulses. International Journal of Difference Equations 2006,1(2):225-239.
Li Y, Fan X, Zhao L: Positive periodic solutions of functional differential equations with impulses and a parameter. Computers & Mathematics with Applications 2008,56(10):2556-2560. 10.1016/j.camwa.2008.05.007
Nieto JJ: Basic theory for nonresonance impulsive periodic problems of first order. Journal of Mathematical Analysis and Applications 1997,205(2):423-433. 10.1006/jmaa.1997.5207
Nieto JJ: Impulsive resonance periodic problems of first order. Applied Mathematics Letters 2002,15(4):489-493. 10.1016/S0893-9659(01)00163-X
Nieto JJ: Periodic boundary value problems for first-order impulsive ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2002,51(7):1223-1232. 10.1016/S0362-546X(01)00889-6
Vatsala AS, Sun Y: Periodic boundary value problems of impulsive differential equations. Applicable Analysis 1992,44(3-4):145-158. 10.1080/00036819208840074
Belarbi A, Benchohra M, Ouahab A: Existence results for impulsive dynamic inclusions on time scales. Electronic Journal of Qualitative Theory of Differential Equations 2005,2005(12):1-22.
Benchohra M, Henderson J, Ntouyas SK, Ouahab A: On first order impulsive dynamic equations on time scales. Journal of Difference Equations and Applications 2004,10(6):541-548. 10.1080/10236190410001667986
Benchohra M, Ntouyas SK, Ouahab A: Existence results for second order boundary value problem of impulsive dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):65-73. 10.1016/j.jmaa.2004.02.057
Geng F, Xu Y, Zhu D: Periodic boundary value problems for first-order impulsive dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(11):4074-4087. 10.1016/j.na.2007.10.038
Graef JR, Ouahab A: Extremal solutions for nonresonance impulsive functional dynamic equations on time scales. Applied Mathematics and Computation 2008,196(1):333-339. 10.1016/j.amc.2007.05.056
Henderson J: Double solutions of impulsive dynamic boundary value problems on a time scale. Journal of Difference Equations and Applications 2002,8(4):345-356. 10.1080/1026190290017405
Li J, Shen J: Existence results for second-order impulsive boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2009,70(4):1648-1655. 10.1016/j.na.2008.02.047
Wang D-B: Positive solutions for nonlinear first-order periodic boundary value problems of impulsive dynamic equations on time scales. Computers & Mathematics with Applications 2008,56(6):1496-1504. 10.1016/j.camwa.2008.02.038
Sun J-P, Li W-T: Positive solutions to nonlinear first-order PBVPs with parameter on time scales. Nonlinear Analysis: Theory, Methods & Applications 2009,70(3):1133-1145. 10.1016/j.na.2008.02.007
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979,28(4):673-688. 10.1512/iumj.1979.28.28046
Sun J-P, Li W-T: Existence and multiplicity of positive solutions to nonlinear first-order PBVPs on time scales. Computers & Mathematics with Applications 2007,54(6):861-871. 10.1016/j.camwa.2007.03.009
Acknowledgment
The authors express their gratitude to the anonymous referee for his/her valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, DB., Guan, W. Multiple Positive Solutions for Nonlinear First-Order Impulsive Dynamic Equations on Time Scales with Parameter. Adv Differ Equ 2009, 830247 (2009). https://doi.org/10.1155/2009/830247
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/830247
 and
and 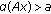
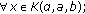



 with
with