- Research Article
- Open access
- Published:
Existence of Weak Solutions for Second-Order Boundary Value Problem of Impulsive Dynamic Equations on Time Scales
Advances in Difference Equations volume 2009, Article number: 907368 (2009)
Abstract
We study the existence of weak solutions for second-order boundary value problem of impulsive dynamic equations on time scales by employing critical point theory.
1. Introduction
Consider the following boundary value problem:




where  is a time scale,
is a time scale,  and
and  is a given function,
is a given function,  are real sequences with
are real sequences with  and
and  the impulsive points
the impulsive points  are right-dense and
are right-dense and  and
and  represent the right and left limits of
represent the right and left limits of  at
at  in the sense of the time scale, that is, in terms of
in the sense of the time scale, that is, in terms of  for which
for which  whereas if
whereas if  is left-scattered, we interpret
is left-scattered, we interpret  and
and  .
.
The theory of time scales, which unifies continuous and discrete analysis, was first introduced by Hilger [1]. The study of boundary value problems for dynamic equations on time scales has recently received a lot of attention, see [2–16]. At the same time, there have been significant developments in impulsive differential equations, see the monographs of Lakshmikantham et al. [17] and Samoĭlenko and Perestyuk [18]. Recently, Benchohra and Ntouyas [19] obtained some existence results for second-order boundary value problem of impulsive differential equations on time scales by using Schaefer's fixed point theorem and nonlinear alternative of Leray-Schauder type. However, to the best of our knowledge, few papers have been published on the existence of solutions for second-order boundary value problem of impulsive dynamic equations on time scales via critical point theory. Inspired and motivated by Jiang and Zhou [10], Nieto and O'Regan [20], and Zhang and Li [21], we study the existence of weak solutions for boundary value problems of impulsive dynamic equations on time scales (1.1)–(1.4) via critical point theory.
This paper is organized as follows. In Section 2, we present some preliminary results concerning the time scales calculus and Sobolev's spaces on time scales. In Section 3, we construct a variational framework for (1.1)–(1.4) and present some basic notation and results. Finally, Section 4 is devoted to the main results and their proof.
2. Preliminaries about Time Scales
In this section, we briefly present some fundamental definitions and results from the calculus on time scales and Sobolev's spaces on time scales so that the paper is self-contained. For more details, one can see [22–25].
Definition 2.1.
A time scale  is an arbitrary nonempty closed subset of
is an arbitrary nonempty closed subset of  equipped with the topology induced from the standard topology on
equipped with the topology induced from the standard topology on 
For 
Definition 2.2.
One defines the forward jump operator  the backward jump operator
the backward jump operator  and the graininess
and the graininess  by
by

respectively. If  then
then  is called right-dense (otherwise: right-scattered), and if
is called right-dense (otherwise: right-scattered), and if  then
then  is called left-dense (otherwise: left-scattered). Denote
is called left-dense (otherwise: left-scattered). Denote 
Definition 2.3.
Assume  is a function and let
is a function and let  Then one defines
Then one defines  to be the number (provided it exists) with the property that given any
to be the number (provided it exists) with the property that given any  there is a neighborhood
there is a neighborhood  of
of  (i.e.,
(i.e.,  for some
for some  ) such that
) such that

In this case,  is called the delta (or Hilger) derivative of
is called the delta (or Hilger) derivative of  at
at  Moreover,
Moreover,  is said to be delta or Hilger differentiable on
is said to be delta or Hilger differentiable on  if
if  exists for all
exists for all 
Definition 2.4.
A function  is said to be rd-continuous if it is continuous at right-dense points in
is said to be rd-continuous if it is continuous at right-dense points in  and its left-sided limits exist (finite) at left-dense points in
and its left-sided limits exist (finite) at left-dense points in  The set of rd-continuous functions
The set of rd-continuous functions  will be denoted by
will be denoted by 
As mentioned in [24], the Lebesgue  -measure can be characterized as follows:
-measure can be characterized as follows:

where  is the Lebesgue measure on
is the Lebesgue measure on  and
and  is the (at most countable) set of all right-scattered points of
is the (at most countable) set of all right-scattered points of  A function
A function  which is measurable with respect to
which is measurable with respect to  is called
is called  -measurable, and the Lebesgue integral over
-measurable, and the Lebesgue integral over  is denoted by
is denoted by

The Lebesgue integral associated with the measure  on
on  is called the Lebesgue delta integral.
is called the Lebesgue delta integral.
Lemma 2.5 (see [24, Theorem 2.11]).
If  are absolutely continuous functions on
are absolutely continuous functions on  , then
, then  is absolutely continuous on
is absolutely continuous on  and the following equality is valid:
and the following equality is valid:

For  , the Banach space
, the Banach space  may be defined in the standard way, namely,
may be defined in the standard way, namely,

equipped with the norm

Let  be the space of the form
be the space of the form

its norm is induced by the inner product given by

for all 
Let  denote the linear space of all continuous function
denote the linear space of all continuous function  with the maximum norm
with the maximum norm 
Lemma 2.6 (see [24, Corollary 3.8]).
Let  , and
, and  If
If  converges weakly in
converges weakly in  to
to  , then
, then  converges strongly in
converges strongly in  to
to  .
.
Lemma 2.7 (Hölder inequality [25, Theorem 3.1]).
Let  and
and  be the conjugate number of
be the conjugate number of  Then
Then

When  we obtain the Cauchy-Schwarz inequality.
we obtain the Cauchy-Schwarz inequality.
For more basic properties of Sobolev's spaces on time scales, one may refer to Agarwal et al. [24].
3. Variational Framework
In this section, we will establish the corresponding variational framework for problem (1.1)–(1.4).
Let  and
and

for 
Now we consider the following space:

its norm is induced by the inner product given by

That is

for any 
First, we give some lemmas which are useful in the proof of theorems.
Lemma 3.1.
If  then for any
then for any  ,
,  where
where 
Proof.
For any  and
and  we have
we have

which implies that

Lemma 3.2.
 is a Hilbert space.
is a Hilbert space.
Proof.
Let  be a Cauchy sequence in
be a Cauchy sequence in  By Lemma 3.1, we have
By Lemma 3.1, we have

Set

for  Then
Then  be a Cauchy sequence in
be a Cauchy sequence in  for
for  Therefore, there exists a
Therefore, there exists a  such that
such that  converges to
converges to  in
in  It follows from Lemma 2.6 that
It follows from Lemma 2.6 that  converges strongly to
converges strongly to  in
in  , that is,
, that is,  as
as  for all
for all  Hence, we have
Hence, we have

Noting that

we have

Set

Then we have

Thus  Noting that
Noting that

we have  converges to
converges to  in
in  as
as  . The proof is complete.
. The proof is complete.
Lemma 3.3.
If  then for any
then for any  ,
,

where  is given in Lemma 3.1.
is given in Lemma 3.1.
Proof.
For any  by Lemma 3.1, we have
by Lemma 3.1, we have

which implies that

The proof is complete.
For any  satisfying (1.1)–(1.4), take
satisfying (1.1)–(1.4), take  and multiply (1.1) by
and multiply (1.1) by  then integrate it between
then integrate it between  and
and  :
:

The first term is now

Hence, one gets

for all  Then we have
Then we have

for all 
This suggests that one defines  by
by

where  and
and 
By a standard argument, one can prove that the functional  is continuously differentiable at any
is continuously differentiable at any  and
and

for all 
We call such critical points weak solutions of problem (1.1)–(1.4).
Let  be a Banach space,
be a Banach space,  which means that
which means that  is a continuously Fréchet-differentiable functional on
is a continuously Fréchet-differentiable functional on  .
.  is said to satisfy the Palais-Smale condition (P-S condition) if any sequence
is said to satisfy the Palais-Smale condition (P-S condition) if any sequence  such that
such that  is bounded and
is bounded and  as
as  has a convergent subsequence in
has a convergent subsequence in 
Lemma 3.4 (Mountain pass theorem [26, Theorem 2.2], [27]).
Let  be a real Hilbert space. Suppose
be a real Hilbert space. Suppose  satisfies the P-S condition and the following assumptions:
satisfies the P-S condition and the following assumptions:
() there exist constants  and
and  such that
such that  for all
for all  where
where  which will be the open ball in
which will be the open ball in  with radius
with radius  and centered at
and centered at 
() and there exists
and there exists  such that
such that  .
.
Then  possesses a critical value
possesses a critical value  Moreover,
Moreover,  can be characterized as
can be characterized as

where

4. Main Results
Now we introduce some assumptions, which are used hereafter:
(H 1) the function  is continuous;
is continuous;
(H 2) holds uniformly for
holds uniformly for 
(H 3) there exist constants  and
and  such that
such that

(H 4) there exist constants  with
with  such that
such that

where  and
and  .
.
Remark 4.1.
 is the well-known Ambrosetti-Rabinowitz condition from the paper [27].
is the well-known Ambrosetti-Rabinowitz condition from the paper [27].
Lemma 4.2.
Suppose that the conditions ( )–(
)–( ) are satisfied, then
) are satisfied, then  satisfies the Palais-Smale condition.
satisfies the Palais-Smale condition.
Proof.
Let  be the sequence in
be the sequence in  satisfying that
satisfying that  is bounded and
is bounded and  as
as  Then there exists a constant
Then there exists a constant  such that
such that

for every  By
By  we know that there exist constants
we know that there exist constants  such that
such that

for all  . By
. By  and Lemma 3.1, we have
and Lemma 3.1, we have


for all  .
.
Set

for 
It follows from (4.3)–(4.5), and  that
that

for some constants  which implies that
which implies that  is bounded by the fact that
is bounded by the fact that  .
.
Then  is bounded in
is bounded in  for
for  Therefore, there exists a subsequence
Therefore, there exists a subsequence  (for simplicity denoted again by
(for simplicity denoted again by  ) such that
) such that  converges weakly to
converges weakly to  in
in  and by Lemma 2.6,
and by Lemma 2.6,  converges strongly to
converges strongly to  in
in  , that is,
, that is,  as
as  for all
for all 
Set

In a similar way to Lemma 3.2, one can prove that 

For any  we have
we have

which implies that  converges weakly to
converges weakly to  in
in  .
.
By (3.22) and (3.23), we have

By the fact that  as
as  and the continuity of
and the continuity of  and
and  on
on  we conclude
we conclude

that is,

Thus,  possesses a convergent subsequence in
possesses a convergent subsequence in  Then, the P-S condition is now satisfied.
Then, the P-S condition is now satisfied.
Theorem 4.3.
Suppose that ( )–(
)–( ) hold. Then problem (1.1)–(1.4) has at least one nontrivial weak solution on
) hold. Then problem (1.1)–(1.4) has at least one nontrivial weak solution on 
Proof.
In order to show that  has at least one nonzero critical point, it suffices to check the conditions
has at least one nonzero critical point, it suffices to check the conditions  and
and  . It follows from
. It follows from  that there is a constant
that there is a constant  such that
such that

for all  and
and  Hence, we have
Hence, we have

for all  and
and  By Lemma 3.3, we obtain
By Lemma 3.3, we obtain

for all  and
and  It follows from (4.5) and (4.16) that
It follows from (4.5) and (4.16) that

for all  and
and  Therefore, by (3.6), one gets
Therefore, by (3.6), one gets

for all  where
where  and
and  Then
Then  is verified. Next we verify
is verified. Next we verify  By (4.4), one has
By (4.4), one has

for all  , and by
, and by  and Lemma 3.1, we have
and Lemma 3.1, we have

for all  and some positive constant
and some positive constant 
Let  and
and  For any
For any  by (4.19) and (4.20), one obtains
by (4.19) and (4.20), one obtains

which implies that

as  for
for  Hence, we can choose sufficiently large
Hence, we can choose sufficiently large  such that
such that  ,
,  and
and  Assumption
Assumption  is verified. Theorem 4.3 is now proved.
is verified. Theorem 4.3 is now proved.
Example 4.4.
Let  Then the system
Then the system

is solvable.
References
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Agarwal RP, Bohner M, Wong PJY: Sturm-Liouville eigenvalue problems on time scales. Applied Mathematics and Computation 1999,99(2-3):153-166. 10.1016/S0096-3003(98)00004-6
Agarwal R, Bohner M, O'Regan D, Peterson A: Dynamic equations on time scales: a survey. Journal of Computational and Applied Mathematics 2002,141(1-2):1-26. 10.1016/S0377-0427(01)00432-0
Amster P, Nápoli PD: Variational methods for two resonant problems on time scales. International Journal of Difference Equations 2007,2(1):1-12.
Anderson DR: Eigenvalue intervals for a two-point boundary value problem on a measure chain. Journal of Computational and Applied Mathematics 2002,141(1-2):57-64. 10.1016/S0377-0427(01)00435-6
Anderson DR, Avery RI: An even-order three-point boundary value problem on time scales. Journal of Mathematical Analysis and Applications 2004,291(2):514-525. 10.1016/j.jmaa.2003.11.013
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002,141(1-2):75-99. 10.1016/S0377-0427(01)00437-X
Cabada A: Extremal solutions and Green's functions of higher order periodic boundary value problems in time scales. Journal of Mathematical Analysis and Applications 2004,290(1):35-54. 10.1016/j.jmaa.2003.08.018
He Z:Existence of two solutions of
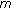 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051Jiang L, Zhou Z: Existence of weak solutions of two-point boundary value problems for second-order dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1376-1388. 10.1016/j.na.2007.06.034
Topal SG: Second-order periodic boundary value problems on time scales. Computers & Mathematics with Applications 2004,48(3-4):637-648. 10.1016/j.camwa.2002.04.005
Cabada A:Existence results for
 -Laplacian boundary value problems on time scales. Advances in Difference Equations 2006, 2006:-11.
-Laplacian boundary value problems on time scales. Advances in Difference Equations 2006, 2006:-11.Davidson FA, Rynne BP: The formulation of second-order boundary value problems on time scales. Advances in Difference Equations 2006, 2006:-10.
Karna B, Lawrence BA: An existence result for a multipoint boundary value problem on a time scale. Advances in Difference Equations 2006, 2006:-8.
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Multiple positive solutions in the sense of distributions of singular BVPs on time scales and an application to Emden-Fowler equations. Advances in Difference Equations 2008, 2008:-13.
Benchohra M, Henderson J, Ntouyas SK: Eigenvalue problems for systems of nonlinear boundary value problems on time scales. Advances in Difference Equations 2007, 2007:-10.
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 14. World Scientific, River Edge, NJ, USA; 1995:x+462.
Benchohra M, Ntouyas SK, Ouahab A: Existence results for second order boundary value problem of impulsive dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):65-73. 10.1016/j.jmaa.2004.02.057
Nieto JJ, O'Regan D: Variational approach to impulsive differential equations. Nonlinear Analysis: Real World Applications 2009,10(2):680-690. 10.1016/j.nonrwa.2007.10.022
Zhang H, Li ZX: Periodic solutions of second-order nonautonomous impulsive differential equations. International Journal of Qualitative Theory of Differential Equations and Applications 2008,2(1):112-124.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introdution with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A: Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Basic properties of Sobolev's spaces on time scales. Advances in Difference Equations 2006, 2006:-14.
Agarwal R, Bohner M, Peterson A: Inequalities on time scales: a survey. Mathematical Inequalities & Applications 2001,4(4):535-557.
Rabinowitz PH: Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics. Volume 65. CBMS AMS, Providence, RI, USA; 1986:viii+100.
Ambrosetti A, Rabinowitz PH: Dual variational methods in critical point theory and applications. Journal of Functional Analysis 1973,14(4):349-381. 10.1016/0022-1236(73)90051-7
Acknowledgment
This research is supported by the National Natural Science Foundation of China (no. 10561004).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Duan, H., Fang, H. Existence of Weak Solutions for Second-Order Boundary Value Problem of Impulsive Dynamic Equations on Time Scales. Adv Differ Equ 2009, 907368 (2009). https://doi.org/10.1155/2009/907368
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/907368
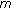 -point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051
-point boundary value problem for second order dynamic equations on time scales. Journal of Mathematical Analysis and Applications 2004,296(1):97-109. 10.1016/j.jmaa.2004.03.051 -Laplacian boundary value problems on time scales. Advances in Difference Equations 2006, 2006:-11.
-Laplacian boundary value problems on time scales. Advances in Difference Equations 2006, 2006:-11.