- Research Article
- Open access
- Published:
Control of Oscillating Systems with a Single Delay
Advances in Difference Equations volume 2010, Article number: 108218 (2010)
Abstract
Systems are considered related to the control of processes described by oscillating second-order systems of differential equations with a single delay. An explicit representation of solutions with the aid of special matrix functions called a delayed matrix sine and a delayed matrix cosine is used to develop the conditions of relative controllability and to construct a specific control function solving the relative controllability problem of transferring an initial function to a prescribed point in the phase space.
1. Introduction
The problem of controllability of linear first-order autonomous systems without delay

with an  constant matrix
constant matrix  ,
,  and
and  is solved by the well-known Kalman criterion (e.g., [1–3]).According to this, for the control of a linear system, it is necessary and sufficient that the rank criterion
is solved by the well-known Kalman criterion (e.g., [1–3]).According to this, for the control of a linear system, it is necessary and sufficient that the rank criterion

should be fulfilled where

A proof is based on two important results. The first is the formula for an integral representation of a solution of a Cauchy problem for the nonhomogeneous system

where

is the matrix exponential (throughout this paper,  stands for an
stands for an  unit matrix). The second is the Cayley-Hamilton theorem saying that any power
unit matrix). The second is the Cayley-Hamilton theorem saying that any power  ,
,  of matrix
of matrix  can be represented by a linear combination of powers
can be represented by a linear combination of powers  ,
,  [4, 5]. We remark that the problem regarding the construction of a control function has a nonunique solution.
[4, 5]. We remark that the problem regarding the construction of a control function has a nonunique solution.
For control systems with delay, a solution to the controllability problem is considerably more complicated. The control function is a functional of a previous phase state. First results related to controllability of linear systems with constant coefficients and a constant delay have been formulated in [6, 7] and, for linear systems with variable coefficients and a variable delay, in [8]. Problems of optimal control of systems with delay are considered in [9, 10]. Recent results on controllability of systems with delay are collected in [11–14].
In this paper, we investigate systems related to control of processes, described by oscillating second-order systems of differential equations with a single delay, in the following form:

where  ,
,  ,
,  is an
is an  constant regular matrix,
constant regular matrix,  ,
,  ,
,  and
and  .
.
One way to investigate such problem is to define additional dependent variables and, transforming initial system (1.6) into a system of first-order linear differential equations with constant coefficients and a constant delay, to get controllability criteria using the results in the above-mentioned sources. However, then the dimension of the auxiliary system equals  and the essential feature of the situation is that we lose an explicit form of influence of the matrix
and the essential feature of the situation is that we lose an explicit form of influence of the matrix  when a control function is designed.
when a control function is designed.
In the paper, special matrix functions, called a delayed matrix cosine and a delayed matrix sine, are utilized. As a motivation for the terminology used calling the analyzed systems "oscillating" served the formal similarity with the partial sums of the defining series for the usual matrix sine and matrix cosine together with the formal parallel between (1.6) and systems of ordinary differential equations describing oscillating processes ((1.6) with  ).
).
The main result is the construction of a control function (in terms of these matrix functions), solving the problem of a transferring of an initial function to a prescribed point in the phase space.
2. Preliminaries
For a solution to the control problem, we need formulas to represent the solutions of an oscillating system with a single delay. First we discuss a linear nonhomogeneous differential system with a single delay

where the meaning of  ,
,  ,
,  and
and  is the same as in (1.6), and
is the same as in (1.6), and  . Below we use the symbols
. Below we use the symbols  and
and  . The symbol
. The symbol  stands for an
stands for an  zero matrix and the symbol
zero matrix and the symbol  stands for the
stands for the  vector
vector  .
.
In [15], system (2.1) was investigated and a representation of its solutions was derived using special matrix functions called a delayed matrix sine and a delayed matrix cosine. With their help, it was possible to derive a representation of the solutions of Cauchy problems. We state the basic definitions, formulated in [15], needed for a solution of the control problem described in Part 3.
Definition 2.1.
The matrix function  , continuous on
, continuous on  , and defined as
, and defined as

is called a delayed matrix cosine.
Definition 2.2.
The matrix function  , continuous on
, continuous on  , and defined as
, and defined as

is called a delayed matrix sine.
With the use of the above-defined special matrices, a solution of the Cauchy problem for nonhomogeneous system with a single delay can be written in an integral form. We recall the rules for computing the derivatives necessary for our investigation of  and
and  [15]. We remark that, in Definitions 2.1 and 2.2 as well as in formulas (2.4), (2.5) below, the matrix
[15]. We remark that, in Definitions 2.1 and 2.2 as well as in formulas (2.4), (2.5) below, the matrix  can even be singular.
can even be singular.
Lemma 2.3.
The following formulas are true for a delayed matrix cosine and a delayed matrix sine:


The following theorem can be proved directly using formulas (2.4) and (2.5). A particular case of this result (when  ) is given in [15]. Therefore, we omit the proof.
) is given in [15]. Therefore, we omit the proof.
Theorem 2.4.
Let  be continuously differentiable vector functions and
be continuously differentiable vector functions and  a locally integrable vector function. Then the solution
a locally integrable vector function. Then the solution  of the Cauchy problem
of the Cauchy problem

for the nonhomogeneous system (2.1) has the form

on  .
.
3. Control of Oscillating Systems
In this part, we investigate the control problem and give the construction of a control function for oscillating systems with a single delay (1.6) within the meaning of the following definition. Since (1.6) is a second-order system, an initial Cauchy problem, in general, should fix  independent initial one-dimensional functions. For this reason, in the formulation of an initial Cauchy problem below, we prescribe initial vectors for the solution and its first derivative.
independent initial one-dimensional functions. For this reason, in the formulation of an initial Cauchy problem below, we prescribe initial vectors for the solution and its first derivative.
Definition 3.1.
System (1.6) is relatively controllable if for any continuously differentiable initial vector functions  , any finite terminal conditions
, any finite terminal conditions  , and any sufficiently large terminal point
, and any sufficiently large terminal point  , there exists a control
, there exists a control  such that the system (1.6) with the input
such that the system (1.6) with the input  , that is, the system
, that is, the system

has a solution  such that
such that




To investigate the problem (3.1)–(3.5), we need some auxiliary notions given below.
Definition 3.2.
We call the pair  controllable if
controllable if  where
where

Definition 3.3.
Let a positive number  be given. We define the class of all uniformly bounded and piecewise-continuous functions on
be given. We define the class of all uniformly bounded and piecewise-continuous functions on  ,
,  (called a control set )
(called a control set )  as
as

where  and
and

Definition 3.4.
The domain

where  and
and  is a solution of (1.6) corresponding to the fixed initial conditions
is a solution of (1.6) corresponding to the fixed initial conditions

and to an arbitrary control  , is called a domain of reachability (reachable set) with respect to the time
, is called a domain of reachability (reachable set) with respect to the time  and the functions
and the functions  ,
,  .
.
We introduce a  -dimensional auxiliary vector
-dimensional auxiliary vector  :
:

and  -dimensional auxiliary vectors
-dimensional auxiliary vectors


Before formulating the results on a relative controllability of (1.6), we present some auxiliary propositions.
Lemma 3.5.
Let the pair  be controllable. Then, on an arbitrary interval
be controllable. Then, on an arbitrary interval  with
with  , the coordinates of the vector function
, the coordinates of the vector function  are linearly independent, that is, there is no nonzero constant vector
are linearly independent, that is, there is no nonzero constant vector

such that

for every  .
.
Proof.
Suppose, on the contrary, that there exists a nonzero vector (3.14) such that (3.15) holds for every  , that is,
, that is,

We will analyse the identity (3.16). Using Definition 2.1 of a delayed matrix cosine and Definition 2.2 of a delayed matrix sine, we obtain

Considering identities (3.17) for  and taking into account the fact that the left-hand side of (3.17) is, on every interval
and taking into account the fact that the left-hand side of (3.17) is, on every interval  ,
,  , a polynomial in
, a polynomial in  having only a finite number of zero points, we conclude that identity (3.17) is only true in the case of polynomials having all their coefficients equal to zero. In other words, we get the conditions
having only a finite number of zero points, we conclude that identity (3.17) is only true in the case of polynomials having all their coefficients equal to zero. In other words, we get the conditions


The homogeneous systems (3.18), (3.19) have a nonzero solution if and only if their determinants are equal to zero, that is,  or
or  . This contradicts the assumption of controllability of the pair
. This contradicts the assumption of controllability of the pair  .
.
Lemma 3.6.
If a vector function  consists of linearly independent elements on the interval
consists of linearly independent elements on the interval  where
where  , then
, then

Proof.
The statement is a consequence of the fact that the symmetric matrix

is positively definite and thus regular.
Remark 3.7.
Note that it is easy to see that the matrix  is (unlike the matrix (3.21)) singular for every
is (unlike the matrix (3.21)) singular for every  .
.
Now we are able to present a result on the relative controllability of system (1.6), and give an inequality for the value  , mentioned in Definition 3.1.
, mentioned in Definition 3.1.
Theorem 3.8.
System (1.6) is relatively controllable if and only if  and the pair
and the pair  is controllable.
is controllable.
Proof.
Let the system (1.6) be relatively controllable within the meaning of Definition 3.1. We use the representation formula for a solution of the Cauchy problem for nonhomogeneous equation in the form (2.7) for the control  (i.e.
(i.e.  ) and time
) and time  . We obtain
. We obtain


Equation (3.22) and (3.23) can be rewritten as a system of the two following equations:


where  ,
,  are defined by (3.12) and (3.13).
are defined by (3.12) and (3.13).
We will investigate the system (3.24). Let, for an integer  ,
,  . We use the representation of a delayed matrix sine and, after putting
. We use the representation of a delayed matrix sine and, after putting  , the left-hand side of (3.24) equals
, the left-hand side of (3.24) equals

We denote

Using (3.27) and the regularity of the matrix  , we rewrite the system (3.24) in the form
, we rewrite the system (3.24) in the form

Now we go on analysing the system (3.25). Let, as in the previous case, for an integer  ,
,  . We use the representation of a delayed matrix cosine and, after putting
. We use the representation of a delayed matrix cosine and, after putting  , we obtain
, we obtain

We denote

Using (3.30) and the regularity of the matrix  , we rewrite the system (3.25) in the form
, we rewrite the system (3.25) in the form

It was assumed that the system (1.6) is relatively controllable. Consequently, systems (3.28) and (3.31) have solutions for arbitrary vectors  ,
,  . If
. If  or
or  and
and  , then both systems are overdetermined and the existence of a solution is not guaranteed.Therefore, for (1.6) to be relatively controllable, it is necessary that
, then both systems are overdetermined and the existence of a solution is not guaranteed.Therefore, for (1.6) to be relatively controllable, it is necessary that  and, if
and, if  , then
, then  , that is,
, that is,

A simple consequence of Cayley-Hamilton theorem (e.g. [5]) is that an arbitrary degree  ,
,  of the matrix
of the matrix  can be represented as a linear combination of matrices
can be represented as a linear combination of matrices

Then, for  , both systems (3.28) and (3.31) can be replaced by the systems
, both systems (3.28) and (3.31) can be replaced by the systems


where  ,
,  are some new functions depending on
are some new functions depending on  . If systems (3.34) and (3.35) have solutions
. If systems (3.34) and (3.35) have solutions

for an arbitrary choice of  ,
,  , then
, then  , that is, the pair
, that is, the pair  is controllable. The necessity is proved.
is controllable. The necessity is proved.
Sufficiency. The proof almost fully copies a known proof of sufficiency for linear systems without delay. Due to the linearity of the problem considered, we can assume, without loss of generality, that the initial functions are zero vector-functions, that is,

In addition to this,  and the controllability of
and the controllability of  is assumed. We prove that the system (1.6), is relatively controllable.
is assumed. We prove that the system (1.6), is relatively controllable.
First we prove that the domain of reachability  has a dimension of
has a dimension of  if
if  . Let, on the contrary,
. Let, on the contrary,  . Then, there exists a fixed vector
. Then, there exists a fixed vector  ,
,

such that, for an arbitrary  , for the relevant solution
, for the relevant solution  of (1.6) we have
of (1.6) we have

Since the initial functions are zero vector-functions, condition (3.39) turns, due to formula (2.7) with  , into
, into

Because (3.40) is satisfied for an arbitrary function  , we deduce, by the fundamental lemma of the calculus of variations, that
, we deduce, by the fundamental lemma of the calculus of variations, that

or, after putting  , we have
, we have

This contradicts the statement of Lemma 3.5 with  . Thus, the assumption that the dimension of
. Thus, the assumption that the dimension of  is smaller than
is smaller than  is false.
is false.
Since the domain of reachability  together with a point
together with a point  corresponding to a control
corresponding to a control  also contains a point
also contains a point  (corresponding to a control
(corresponding to a control  ), we conclude that
), we conclude that  is symmetric. Due to the linearity of the problem considered, it is also a convex domain. Consequently, it contains a ball with a radius of
is symmetric. Due to the linearity of the problem considered, it is also a convex domain. Consequently, it contains a ball with a radius of  .
.
Obviously, if we consider the control set  instead of
instead of  and
and  , then
, then  , that is,
, that is,  . Simultaneously, it says that, for every point
. Simultaneously, it says that, for every point  , there exists a control
, there exists a control  such that the solution
such that the solution  of (3.1) satisfies (3.2)–(3.5).
of (3.1) satisfies (3.2)–(3.5).
This conclusion remains valid even in the case of any nonidentically zero initial functions. Indeed, a simple transformation  where
where  is a new dependent function and
is a new dependent function and  is a solution of a homogeneous problem
is a solution of a homogeneous problem

leads to the same problem with respect to  with zero initial vector-functions. Thus, the system (1.6) is relatively controllable.
with zero initial vector-functions. Thus, the system (1.6) is relatively controllable.
Now we give the formula for a relevant control function. An advantage of the result obtained is an explicit dependence of the control function on the delayed matrix cosine and delayed matrix sine.
Theorem 3.9.
Let  and let the pair
and let the pair  be controllable. Then, a control function relevant to the problem (3.1)–(3.5) can be thought of as having the form
be controllable. Then, a control function relevant to the problem (3.1)–(3.5) can be thought of as having the form

where  ,
, and
and arethe solutions of a system of linear nonhomogeneous algebraic equations
arethe solutions of a system of linear nonhomogeneous algebraic equations

where  matrices
matrices  ,
,  are defined as
are defined as

and vectors  ,
,  are defined by (3.13).
are defined by (3.13).
Proof.
Let  . Since the pair
. Since the pair  is controllable, the vectors
is controllable, the vectors

are linearly independent. From the integral representation (2.7), it follows that the terminal values of a solution  of system (1.6) at
of system (1.6) at  satisfying initial conditions (3.2) and (3.3) have the form (3.22) and (3.23). Therefore, a suitable control function
satisfying initial conditions (3.2) and (3.3) have the form (3.22) and (3.23). Therefore, a suitable control function  should satisfy the system of integral equations (3.24) and (3.25). Let us try to find the control function in the form of a linear combination
should satisfy the system of integral equations (3.24) and (3.25). Let us try to find the control function in the form of a linear combination

where  and
and  are unknown constant vectors. We apply representation (3.48) to (3.24), (3.25). Then, we get
are unknown constant vectors. We apply representation (3.48) to (3.24), (3.25). Then, we get

or

with the above defined matrices  ,
,  . The determinant
. The determinant  of the system (3.50) can be written in the form
of the system (3.50) can be written in the form

Using a transformation  in the integral and the denotation (3.11), we get
in the integral and the denotation (3.11), we get

By Lemma 3.5, the coordinates of  are linearly independent on
are linearly independent on  where
where  . Then, by Lemma 3.6 (with
. Then, by Lemma 3.6 (with  ),
),  . Consequently, the system (3.50) has a unique solution
. Consequently, the system (3.50) has a unique solution  ,
,  and the control (3.48) coincides with (3.44).
and the control (3.48) coincides with (3.44).
4. Conclusions and Future Directions
The paper studied the problem of the relative controllability of oscillating systems (1.6) within the meaning of Definition 3.1. An explicit representation of solutions of (1.6) with the aid of special matrix functions called a delayed matrix sine and a delayed matrix cosine was used to solve this problem. The necessary and sufficient conditions of relative controllability were derived and a specific control function was constructed in terms of these matrix functions, solving the relative controllability problem of transferring an initial function to a prescribed point in the phase space. Some previous results of investigating the controllability problems using special matrix functions were derived for linear delayed systems with a single delay in [16] (the case of continuous systems) and in [17] (the case of discrete systems) where representations of solutions of linear discrete systems [18, 19] are used. It is an open problem how to extend the results derived to systems of discrete equations with a single delay

where  is an independent variable,
is an independent variable,  is a positive integer, and (4.1) is a discrete analogy of (1.6). Another open problem is how to extend the results derived to fractional systems (see, e.g., [20]).
is a positive integer, and (4.1) is a discrete analogy of (1.6). Another open problem is how to extend the results derived to fractional systems (see, e.g., [20]).
References
Kalman RE: On the general theory of control systems. Proceedings of the 1st International Congress of IFAC, 1961, Moscow, Russia 2: Izd. AN SSSR
Kalman RE, Falb PL, Arbib MA: Topics in Mathematical System Theory, Pure and Applied Mathematics. McGraw-Hill, New York, NY, USA; 1969:xiv+358.
Athans M, Falb PL: Optimal Control. An Introduction to the Theory and Its Applications, Electrical and Electronik Engineering Series. McGraw-Hill, New York, NY, USA; 1966:xiv+879.
Bernstein DS: Matrix Mathematics. Princeton University Press, Princeton, NJ, USA; 2005:xxxviii+726.
Gantmacher FP: The Theory of Matrices. Volume 1. AMS Chelsea Publishing, Providence, RI, USA; 2002.
Kirillova FM, Churakova SV: On the problem of controllability of linear systems with aftereffect. Differencial'nye Uravnenija 1967, 3: 436-445. English translation in Differential Equations, vol. 3, no. 3, pp. 221–225, 1967
Kirillova FM, Churakova SV: Relative controllability of linear dynamic sytems with lag. Doklady Akademii Nauk SSSR 1967, 174: 1260-1263. English translation in Soviet Mathematics-Doklady, vol. 8, no. 3, pp. 748–7581, 1967
Kirillova FM: Relative controllability of linear systems with variable and distributed time lags. Differencial'nye Uravnenija 1966,5(6):1068-1075.
Gabasov R, Churakova SV: An optimal control in systems with aftereffect. Differencial'nye Uravnenija 1966,2(10):1286-1299. English translation in Differential Equations, An optimal control in systems with aftereffect, vol. 3, no. 3, pp. 668–672, 1966
Gabasov R, Kirillova FM: The Qualitative Theory of Optimal Control. Marcel Dekker, New York, NY, USA; 1976.
Boukas E-K, Liu Z-K: Deterministic and Stochastic Time Delay Systems. Birkhäuser, Boston, Mass, USA; 2002.
Chiasson J: Applications of Time Delay Systems, Lecture Notes in Control and Information Sciences. Volume 352. Springer, Berlin, Germany; 2007:xii+358.
Chukwu EN: Stability and Time-Optimal Control of Hereditary Systems, Series on Advances in Mathematics for Applied Sciences. Volume 60. 2nd edition. World Scientific Publishing, River Edge, NJ, USA; 2001:xx+495.
Michiels W, Niculescu S-L: Stability and Stabilization of Time-Delay Systems, Advances in Design and Control. Volume 12. SIAM, Philadelphia, Pa, USA; 2007:xxii+378.
Khusainov DYa, Diblík J, Růžičková M, Lukáčová J: A representation of the solution of the Cauchy problem for an oscillatory system with pure delay. Nelinijni Kolyvannya 2008,11(2):261-270. English translation in Nonlinear Oscillations, Representation of a solution of the Cauchy problem for an oscillating system with pure delay, vol. 11, no. 2, pp. 276–285, 2008
Khusainov DYa, Shuklin GV: On relative controllability in systems with pure delay. Prikladnaya Mekhanika 2005,41(2):118-130. translation in International Applied Mechanics, vol. 41, no. 2, pp. 210–221, 2005
Diblík J, Khusainov DYa, Růžičková M: Controllability of linear discrete systems with constant coefficients and pure delay. SIAM Journal on Control and Optimization 2008,47(3):1140-1149. 10.1137/070689085
Diblík J, Khusainov DYa:Representation of solutions of discrete delayed system
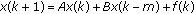 with commutative matrices. Journal of Mathematical Analysis and Applications 2006,318(1):63-76. 10.1016/j.jmaa.2005.05.021
with commutative matrices. Journal of Mathematical Analysis and Applications 2006,318(1):63-76. 10.1016/j.jmaa.2005.05.021Diblík J, Khusainov DYa: Representation of solutions of linear discrete systems with constant coefficients and pure delay. Advances in Difference Equations 2006, 2006:-13.
Ahmed HM: Boundary Controllability of nonlinear fractional integrodifferential systems. to appear in Advances in Difference Equations
Acknowledgments
J. Diblik was supported by Grant 201/08/0469 of Czech Grant Agency (Prague) and by the Councils of Czech Government MSM 00216 30503, MSM 00216 30519 and MSM 00216 30529. D. Ya. Khusainov was supported by project M/34-2008 MOH Ukraine since 27.03.2008. J. Lukáčová was supported by project APVV-0700-07 of Slovak Research and Development Agency and by Grant no.1/0090/09 of the Grant Agency of Slovak Republic (VEGA). M. Růžičková was supported by project APVV-0700-07 of Slovak Research and Development Agency and by Grant no.1/0090/09 of the Grant Agency of Slovak Republic (VEGA).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diblík, J., Khusainov, D., Lukáčová, J. et al. Control of Oscillating Systems with a Single Delay. Adv Differ Equ 2010, 108218 (2010). https://doi.org/10.1155/2010/108218
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/108218
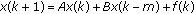 with commutative matrices. Journal of Mathematical Analysis and Applications 2006,318(1):63-76. 10.1016/j.jmaa.2005.05.021
with commutative matrices. Journal of Mathematical Analysis and Applications 2006,318(1):63-76. 10.1016/j.jmaa.2005.05.021