- Research Article
- Open access
- Published:
Elementary Proof of Yu. V. Nesterenko Expansion of the Number Zeta(3) in Continued Fraction
Advances in Difference Equations volume 2010, Article number: 143521 (2010)
Abstract
Yu. V. Nesterenko has proved that  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  for
for  ;
;  ,
,  , and
, and  ,
,  for
for  His proof is based on some properties of hypergeometric functions. We give here an elementary direct proof of this result.
His proof is based on some properties of hypergeometric functions. We give here an elementary direct proof of this result.
1. Foreword
Applications of difference equations to the Number Theory have a long history. For example, one can find in this journal several articles connected with the mentioned applications (see [1–8]). The interest in this area increases after Apéry's discovery of irrationality of the number  This paper is inspired by Yu.V. Nesterenko's work [9]. My goal is to give an elementary direct proof of his expansion of the number
This paper is inspired by Yu.V. Nesterenko's work [9]. My goal is to give an elementary direct proof of his expansion of the number  in continued fraction. Let us consider a difference equation
in continued fraction. Let us consider a difference equation

with  We denote by
We denote by

the solutions of this equation with initial values

Then

is a sequence of convergents of the continued fraction

Accoding to the famous result of R. Apéry [10],

where  and
and  are solutions of difference equation
are solutions of difference equation

with initial values  The equality (1.6) is equivalent to the equality
The equality (1.6) is equivalent to the equality

with

where  Nesterenko in [9] has offered the following expansion of the number
Nesterenko in [9] has offered the following expansion of the number  in continued fraction:
in continued fraction:

with


for 

for 
The halved convergents of continued fraction (1.10) compose a sequence containing convergents of continued fraction (1.8). I give an elementary proof of Yu.V. Nesterenko expansion in Section 2.
2. Elementary Proof of Yu. V. Nesterenko Expansion
Instead of expansion (1.10) with (1.11), it is more convenient for us to prove the equivalent expansion

with

Furthermore, to avoid confusion in notations, we denote below  for the fraction (2.1) by
for the fraction (2.1) by  Let
Let 

where values  are specified in (1.9), and
are specified in (1.9), and  Then
Then

Let 

where  and values
and values  are specified in (2.2), (1.12), and (1.13). We calculate first
are specified in (2.2), (1.12), and (1.13). We calculate first  and
and  for
for 
Since  it follows from (2.2) that
it follows from (2.2) that





Let 

We want to to prove that if  then
then

Note that if  then (2.12) follows from (2.6)–(2.10). Therefore, we can consider only
then (2.12) follows from (2.6)–(2.10). Therefore, we can consider only  Let us consider the following difference equations:
Let us consider the following difference equations:


with  Then
Then  ,
,  with
with  representing a fundamental system of solutions of (2.13), and
representing a fundamental system of solutions of (2.13), and  ,
,  with
with  representing a fundamental system of solutions of (2.14). Making use of standard interpretation of a difference equation as a difference system, we rewrite the equalities (2.13) and (2.14), respectively in the form
representing a fundamental system of solutions of (2.14). Making use of standard interpretation of a difference equation as a difference system, we rewrite the equalities (2.13) and (2.14), respectively in the form


where


and  Let
Let


with  be fundamental matrices of solutions of systems (2.15) and (2.16), respectively. Therefore,
be fundamental matrices of solutions of systems (2.15) and (2.16), respectively. Therefore,

for  In view of (2.18) and (2.21),
In view of (2.18) and (2.21),  and therefore,
and therefore,

Hence

(see [11]).
Further, we have



Let  Then, in view of (2.20),
Then, in view of (2.20),

Let  for
for  In view of (2.16) and (2.18),
In view of (2.16) and (2.18),


where, as before, 

In view of (2.22), (2.2), (1.12), (1.13), (2.29), and (2.28), the matrix  is a fundamental matrix of solutions of system (2.28). The substitution
is a fundamental matrix of solutions of system (2.28). The substitution  with
with  for
for  transforms the system (2.28) into the system
transforms the system (2.28) into the system

with  for
for  We prove now that if we take
We prove now that if we take  and
and  where
where


with  and
and  then we obtain the equality
then we obtain the equality  So, let
So, let  Then, in view of (2.33),
Then, in view of (2.33),

In view of(1.9)

where  Hence, in view of (2.19),
Hence, in view of (2.19),

In view of (2.34)–(2.36),

In view of (2.30) and (2.33),

Since

it follows from (2.35), (2.37), and (2.38) that

for  We prove by induction now the following equality:
We prove by induction now the following equality:

for any  In view of (2.25) and (2.32), the equality (2.41) holds for
In view of (2.25) and (2.32), the equality (2.41) holds for  In view of (2.26) and (2.33), the equality (2.41) hold for
In view of (2.26) and (2.33), the equality (2.41) hold for  Let
Let  and (2.41) holds for
and (2.41) holds for  Then, in view of (2.29), (2.40), and (2.21),
Then, in view of (2.29), (2.40), and (2.21),

So, the equality (2.41) holds for any  In view of (2.41),
In view of (2.41),

for  Since
Since

for  and
and  in (1.6) and
in (1.6) and  it follows from (2.43) and (2.44), that
it follows from (2.43) and (2.44), that

As it is well known, for any  there exist
there exist  and
and  such that
such that



We apply (2.23) now. Let  In view of (2.2), (1.12)–(1.13), and (2.45), if
In view of (2.2), (1.12)–(1.13), and (2.45), if  then
then


In view of (2.23), (2.50), and (2.49), if 

when  In view of (2.45), (2.48), and (2.51), there exist
In view of (2.45), (2.48), and (2.51), there exist  and
and  such that
such that

where  So, the equality (2.1) is proved. In view of (2.23),
So, the equality (2.1) is proved. In view of (2.23),

where

Further, we have

Hence, the series (2.53) is the series of Leibnitz type. Therefore,  decreases, when
decreases, when  increases in
increases in  and
and  increases, when
increases, when  increases in
increases in 
References
Kim T, Hwang K-W, Kim Y-H: Symmetry properties of higher-order Bernoulli polynomials. Advances in Difference Equations 2009, 2009:6.
Kim T, Hwang K-W, Lee B: A note on the
 -Euler measures. Advances in Difference Equations 2009, 2009:8.
-Euler measures. Advances in Difference Equations 2009, 2009:8.Park K-H, Kim Y-H: On some arithmetical properties of the Genocchi numbers and polynomials. Advances in Difference Equations 2008, 2008:14.
Simsek Y, Cangul IN, Kurt V, Curt V, Kim D:
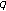 -Genocchi numbers and polynomials associated with
-Genocchi numbers and polynomials associated with  -Genocchi-type
-Genocchi-type  -functions. Advances in Difference Equations 2008, 2008:12.
-functions. Advances in Difference Equations 2008, 2008:12.Jang LC: Multiple twisted
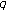 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic 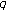 -integrals. Advances in Difference Equations 2008, 2008:11.
-integrals. Advances in Difference Equations 2008, 2008:11.Kim T:
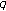 -Bernoulli numbers associated with
-Bernoulli numbers associated with 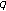 -Stirling numbers. Advances in Difference Equations 2008, 2008:10.
-Stirling numbers. Advances in Difference Equations 2008, 2008:10.Rachidi M, Saeki O: Extending generalized Fibonacci sequences and their Binet-type formula. Advances in Difference Equations 2006, 2006:11.
Jaroma JH: On the appearance of primes in linear recursive sequences. Advances in Difference Equations 2005,2005(2):145-151. 10.1155/ADE.2005.145
Nesterenko YuV: Some remarks on
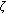 (3). Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki 1996,59(6):865-880.
(3). Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki 1996,59(6):865-880.Apéry R: Interpolation des fractions continues et irrationalité de certaines constantes. Bulletin de la Section des Sciences du C.T.H 1981, 3: 37-53.
Perron O: Die Lehre von den Kettenbrüchen. Bd I. Elementare Kettenbrüche. B. G. Teubner Verlagsgesellschaft, Stuttgart, Germany; 1954:vi+194.
Acknowledgment
The author would like to express his thanks to the reviewer of this article for his efforts, his criticism, his advices, and indications of misprints. Ravi P. Agarwal had expressed a useful suggestion, which the author realized in foreword and references. He is grateful to him in this connection.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gutnik, L. Elementary Proof of Yu. V. Nesterenko Expansion of the Number Zeta(3) in Continued Fraction. Adv Differ Equ 2010, 143521 (2010). https://doi.org/10.1155/2010/143521
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/143521
 -Euler measures. Advances in Difference Equations 2009, 2009:8.
-Euler measures. Advances in Difference Equations 2009, 2009:8.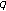 -Genocchi numbers and polynomials associated with
-Genocchi numbers and polynomials associated with  -Genocchi-type
-Genocchi-type  -functions. Advances in Difference Equations 2008, 2008:12.
-functions. Advances in Difference Equations 2008, 2008:12.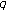 -Euler numbers and polynomials associated with
-Euler numbers and polynomials associated with  -adic
-adic 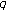 -integrals. Advances in Difference Equations 2008, 2008:11.
-integrals. Advances in Difference Equations 2008, 2008:11.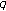 -Bernoulli numbers associated with
-Bernoulli numbers associated with 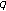 -Stirling numbers. Advances in Difference Equations 2008, 2008:10.
-Stirling numbers. Advances in Difference Equations 2008, 2008:10.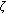 (3). Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki 1996,59(6):865-880.
(3). Rossiĭskaya Akademiya Nauk. Matematicheskie Zametki 1996,59(6):865-880.