- Research Article
- Open access
- Published:
Stabilities of Cubic Mappings in Fuzzy Normed Spaces
Advances in Difference Equations volume 2010, Article number: 150873 (2010)
Abstract
Rassias(2001) introduced the pioneering cubic functional equation in the history of mathematical analysis:  and solved the pertinent famous Ulam stability problem for this inspiring equation. This Rassias cubic functional equation was the historic transition from the following famous Euler-Lagrange-Rassias quadratic functional equation:
and solved the pertinent famous Ulam stability problem for this inspiring equation. This Rassias cubic functional equation was the historic transition from the following famous Euler-Lagrange-Rassias quadratic functional equation:  to the cubic functional equations. In this paper, we prove the Ulam-Hyers stability of the cubic functional equation:
to the cubic functional equations. In this paper, we prove the Ulam-Hyers stability of the cubic functional equation:  in fuzzy normed linear spaces. We use the definition of fuzzy normed linear spaces to establish a fuzzy version of a generalized Hyers-Ulam-Rassias stability for above equation in the fuzzy normed linear space setting. The fuzzy sequentially continuity of the cubic mappings is discussed.
in fuzzy normed linear spaces. We use the definition of fuzzy normed linear spaces to establish a fuzzy version of a generalized Hyers-Ulam-Rassias stability for above equation in the fuzzy normed linear space setting. The fuzzy sequentially continuity of the cubic mappings is discussed.
1. Introduction
Studies on fuzzy normed linear spaces are relatively recent in the field of fuzzy functional analysis. The notion of fuzzyness has a wide application in many areas of science. In 1984, Katsaras [1] first introduced a definition of fuzzy norm on a linear space. Later, several notions of fuzzy norm have been introduced and discussed from different points of view [2, 3]. Concepts of sectional fuzzy continuous mappings and strong uniformly convex fuzzy normed linear spaces have been introduced by Bag and Samanta [4]. Bag and Samanta [5] introduced a notion of boundedness of a linear operator between fuzzy normed spaces, and studied the relation between fuzzy continuity and fuzzy boundedness. They studied boundedness of linear operators over fuzzy normed linear spaces such as fuzzy continuity, sequential fuzzy continuity, weakly fuzzy continuity and strongly fuzzy continuity.
The problem of stability of functional equation originated from a question of Ulam [6] concerning the stability of group homomorphism in 1940. Hyers gave a partial affirmative answer to the question of Ulam for Banach spaces in the next year [7]. Let  and
and  be Banach spaces. Assume that
be Banach spaces. Assume that  satisfies
satisfies  for all
for all  and some
and some  . Then, there exists a unique additive mapping
. Then, there exists a unique additive mapping  such that
such that  for all
for all  .
.  theorem was generalized by Aoki [8] for additive mappings. In 1978, a generalized solution for approximately linear mappings was given by Th. M. Rassias [9]. He considered a mapping
theorem was generalized by Aoki [8] for additive mappings. In 1978, a generalized solution for approximately linear mappings was given by Th. M. Rassias [9]. He considered a mapping  satisfying the condition
satisfying the condition

for all  , where
, where  and
and  . This result was later extended to all
. This result was later extended to all  .
.
In 1982, J. M. Rassias [10] gave a further generalization of the result of Hyers and prove the following theorem using weaker conditions controlled by a product of powers of norms. Let  be a mapping from a normed vector space
be a mapping from a normed vector space  into a Banach space
into a Banach space  subject to the inequality
subject to the inequality

for all  , where
, where  and
and  . Then there exists a unique additive mapping
. Then there exists a unique additive mapping  which satisfies
which satisfies

for all  . The above mentioned stability involving a product of powers of norms is called Ulam–Gavruta–Rassias stability by various authors [11–25].
. The above mentioned stability involving a product of powers of norms is called Ulam–Gavruta–Rassias stability by various authors [11–25].
In 2008, J. M. Rassias [26] generalized even further the above two stabilities via a new stability involving a mixed product-sum of powers of norms, called JMRassias stability by several authors [27–30].
In the last two decades, several form of mixed type functional equation and its Ulam–Hyers stability are dealt in various spaces like Fuzzy normed spaces, Random normed spaces, Quasi–Banach spaces, Quasinormed linear spaces and Banach algebra by various authors like [31–40].
In 1994, Cheng and Mordeson [2] introduced an idea of a fuzzy norm on a linear space whose associated metric is Kramosil and Michálek type [41]. Since then some mathematicians have defined fuzzy metrics and norms on a linear space from various points of view [42–44].
In 2001, J. M. Rassias [45] introduced the pioneering cubic functional equation in history of mathematical analysis, as follows:

and solved the famous Ulam stability problem for this inspiring functional equation. Note that this cubic functional equation (*) was the historic transition from the following famous Euler-Lagrange quadratic functional equation:

to the cubic functional equation (*).
The notion of fuzzy stability of the functional equations was initiated by Mirmostafaee and Moslehian in [46]. Later, several various fuzzy versions of stability were investigated [47, 48]. Now, let us introduce the following functional equation:

Since the cubic function  satisfies in this equation, so we promise that (1.5) is called a cubic functional equation and every solution will be called a cubic function. The stability problem for the cubic functional equation was proved by Wiwatwanich and Nakmahachalasint [49] for mapping
satisfies in this equation, so we promise that (1.5) is called a cubic functional equation and every solution will be called a cubic function. The stability problem for the cubic functional equation was proved by Wiwatwanich and Nakmahachalasint [49] for mapping  , where
, where  and
and  are real Banach spaces. A number of mathematicians worked on the stability of some types of the cubic equation [45, 50–54]. In [55], Park and Jung introduced a cubic functional equation different from (1.5) as follows:
are real Banach spaces. A number of mathematicians worked on the stability of some types of the cubic equation [45, 50–54]. In [55], Park and Jung introduced a cubic functional equation different from (1.5) as follows:

and investigated the generalized Hyers-Ulam-Rassias stability for this equation on abelian groups. They also obtained results in sense of Hyers-Ulam stability and Hyers-Ulam-Rassias stability. A number of results concerning the stability of different functional equations can be found in [23, 56–59].
In this paper, we prove the Hyers-Ulam-Rassias stability of the cubic functional equation (1.5) in fuzzy normed spaces. Later, we will show that there exists a close relationship between the fuzzy sequentially continuity behavior of a cubic function, control function and the unique cubic mapping which approximates the cubic map.
2. Notation and Preliminary Results
In this section some definitions and preliminary results are given which will be used in this paper. Following [48], we give the following notion of a fuzzy norm.
Definition 2.1.
Let  be a linear space. A fuzzy subset
be a linear space. A fuzzy subset  of
of  into
into  is called a fuzzy norm on
is called a fuzzy norm on  if for every
if for every  and
and 
(N1)  for
for  ,
,
(N2)  if and only if
if and only if  for all
for all  ,
,
(N3)  if
if  ,
,
(N4)  ,
,
(N5)  is a non-decreasing function on
is a non-decreasing function on  and
and  .
.
The pair  will be referred to as a fuzzy normed linear space. One may regard
will be referred to as a fuzzy normed linear space. One may regard  as the truth value of the statement "the norm of
as the truth value of the statement "the norm of  is less than or equal to the real number r ". Let
is less than or equal to the real number r ". Let  be a normed linear space. One can be easily verify that
be a normed linear space. One can be easily verify that

is a fuzzy norm on  . Other examples of fuzzy normed linear spaces are considered in the main text of this paper.
. Other examples of fuzzy normed linear spaces are considered in the main text of this paper.
Note that the fuzzy normed linear space  is exactly a Menger probabilistic normed linear space
is exactly a Menger probabilistic normed linear space  where
where  [60].
[60].
Definition 2.2.
A sequence  in a fuzzy normed space
in a fuzzy normed space  converges to
converges to  (one denote
(one denote  ) if for every
) if for every  and
and  , there exists a positive integer
, there exists a positive integer  such that
such that  whenever
whenever  .
.
Recall that, a sequence  in
in  is called Cauchy if for every
is called Cauchy if for every  and
and  , there exists a positive integer
, there exists a positive integer  such that for all
such that for all  and all
and all  , we have
, we have  . It is known that every convergent sequence in a fuzzy normed space is Cauchy. The fuzzy normed space
. It is known that every convergent sequence in a fuzzy normed space is Cauchy. The fuzzy normed space  is said to be fuzzy Banach space if every Cauchy sequence in
is said to be fuzzy Banach space if every Cauchy sequence in  is convergent to a point in
is convergent to a point in  [46].
[46].
3. Main Results
We will investigate the generalized Hyers-Ulam type theorem of the functional equation (1.5) in fuzzy normed spaces. In the following theorem, we will show that under special circumstances on the control function  , every
, every  -almost cubic mapping
-almost cubic mapping  can be approximated by a cubic mapping
can be approximated by a cubic mapping  .
.
Theorem 3.1.
Let  . Let
. Let  be a linear space, and let
be a linear space, and let  be a fuzzy normed space. Suppose that an even function
be a fuzzy normed space. Suppose that an even function  satisfies
satisfies  for all
for all  and for all
and for all  . Suppose that
. Suppose that  is a fuzzy Banach space. If a function
is a fuzzy Banach space. If a function  satisfies
satisfies

for all  and
and  , then there exists a unique cubic function
, then there exists a unique cubic function  which satisfies (1.5) and the inequality
which satisfies (1.5) and the inequality

holds for all  and
and  .
.
Proof.
We have the following two cases.
Case 1 ( ).
).
Replacing  by
by  in (3.1) and summing the resulting inequality with (3.1), we get
in (3.1) and summing the resulting inequality with (3.1), we get

Since (3.1) and (3.3) hold for any  , let us fix
, let us fix  for convenience. By (
for convenience. By ( ), we have
), we have

Replacing  by
by  in (3.4). By (
in (3.4). By ( ), we have
), we have

Replacing  by
by  in (3.5), we get
in (3.5), we get

It follows from

and last inequality that

In order to prove convergence of the sequence  , we replace
, we replace  by
by  to find that for
to find that for  ,
,

Replacing  by
by  in last inequality to get
in last inequality to get

For every  and
and  , we put
, we put

Replacing  by
by  in last inequality, we observe that
in last inequality, we observe that

Let  and
and  be given. Since
be given. Since  , there is some
, there is some  such that
such that  for every
for every  . The convergence of the series
. The convergence of the series  gives some
gives some  such that
such that  for every
for every  and
and  . For every
. For every  and
and  , we have
, we have

This shows that  is a Cauchy sequence in the fuzzy Banach space
is a Cauchy sequence in the fuzzy Banach space  , therefore this sequence converges to some point
, therefore this sequence converges to some point  . Fix
. Fix  and put
and put  in (3.13) to obtain
in (3.13) to obtain

For every  ,
,

The first two terms on the right hand side of the above inequality tend to 1 as  . Therefore we have
. Therefore we have

for  large enough. By last inequality, we have
large enough. By last inequality, we have

Now, we show that  is cubic. Use inequality (3.1) with
is cubic. Use inequality (3.1) with  replaced by
replaced by  and
and  by
by  to find that
to find that

On the other hand  , hence by (
, hence by ( )
)

We conclude that  fulfills (1.5). It remains to prove the uniqueness assertion. Let
fulfills (1.5). It remains to prove the uniqueness assertion. Let  be another cubic mapping satisfying (3.17). Fix
be another cubic mapping satisfying (3.17). Fix  . Obviously
. Obviously

for all  . For every
. For every  , we can write
, we can write

Since  , we have
, we have

Therefore  for all
for all  , whence
, whence  .
.
Case 2 ( ).
).
We can state the proof in the same pattern as we did in the first case. Replace  ,
,  by
by  and
and  , respectively in (3.4) to get
, respectively in (3.4) to get

We replace  and
and  by
by  and
and  in last inequality, respectively, we find that
in last inequality, respectively, we find that

For each  , one can deduce
, one can deduce

where  . It is easy to see that
. It is easy to see that  is a Cauchy sequence in (
is a Cauchy sequence in ( ). Since
). Since  is a fuzzy Banach space, this sequence converges to some point
is a fuzzy Banach space, this sequence converges to some point  , that is,
, that is,

Moreover,  satisfies (1.5) and
satisfies (1.5) and

The proof for uniqueness of  for this case proceeds similarly to that in the previous case, hence it is omitted.
for this case proceeds similarly to that in the previous case, hence it is omitted.
We note that  need not be equal to 27. But we do not guarantee whether the cubic equation is stable in the sense of Hyers, Ulam and Rassias if
need not be equal to 27. But we do not guarantee whether the cubic equation is stable in the sense of Hyers, Ulam and Rassias if  is assumed in Theorem 3.1.
is assumed in Theorem 3.1.
Remark 3.2.
Let  . Suppose that the mapping
. Suppose that the mapping  from
from  into
into  is right continuous. Then we get a fuzzy approximation better than (3.17) as follows.
is right continuous. Then we get a fuzzy approximation better than (3.17) as follows.
For every  , we have
, we have

for large enough  . It follows that
. It follows that

Tending  to zero we infer
to zero we infer

From Theorem 3.1, we obtain the following corollary concerning the stability of (1.5) in the sense of the JMRassias stability of functional equations controlled by the mixed product-sum of powers of norms introduced by J. M. Rassias [26] and called JMRassias stability by several authors [27–30].
Corollary 3.3.
Let  be a Banach space and let
be a Banach space and let  be a real number. Suppose that a function
be a real number. Suppose that a function  satisfies
satisfies

for all  where
where  . Then there exists a unique cubic function
. Then there exists a unique cubic function  which satisfying (1.5) and the inequality
which satisfying (1.5) and the inequality

for all  . The function
. The function  is given by
is given by  for all
for all 
Proof.
Define  by
by

It is easy to see that  is a fuzzy Banach space. Denote by
is a fuzzy Banach space. Denote by  the map sending each
the map sending each  to
to  . By assumption,
. By assumption,

Note that  given by
given by

is a fuzzy norm on  . By Theorem 3.1, there exists a unique cubic function
. By Theorem 3.1, there exists a unique cubic function  satisfies (1.5) and inequality
satisfies (1.5) and inequality

for all  and
and  . Consequently,
. Consequently,  .
.
Definition 3.4.
Let  be a mapping where
be a mapping where  and
and  are fuzzy normed spaces.
are fuzzy normed spaces.  is said to be sequentially fuzzy continuous at
is said to be sequentially fuzzy continuous at  if for any
if for any  satisfying
satisfying  implies
implies  . If
. If  is sequentially fuzzy continuous at each point of
is sequentially fuzzy continuous at each point of  , then
, then  is said to be sequentially fuzzy continuous on
is said to be sequentially fuzzy continuous on  .
.
For the various definitions of continuity and also defining a topology on a fuzzy normed space we refer the interested reader to [61, 62]. Now we examine some conditions under which the cubic mapping found in Theorem 3.1 to be continuous. In the following theorem, we investigate fuzzy sequentially continuity of cubic mappings in fuzzy normed spaces. Indeed, we will show that under some extra conditions on Theorem 3.1, the cubic mapping  is fuzzy sequentially continuous.
is fuzzy sequentially continuous.
Theorem 3.5.
Denote  the fuzzy norm obtained as Corollary 3.3 on
the fuzzy norm obtained as Corollary 3.3 on  . Suppose that conditions of Theorem 3.1 hold. If for every
. Suppose that conditions of Theorem 3.1 hold. If for every  the mappings
the mappings  (from
(from  into
into  and
and  (from
(from  into
into  are sequentially fuzzy continuous, then the mapping
are sequentially fuzzy continuous, then the mapping  is sequentially continuous and
is sequentially continuous and  for all
for all  .
.
Proof.
We have the following case.
Case 1 ( ).
).
Let  be a sequence in
be a sequence in  that converges to some
that converges to some  , and let
, and let  . Let
. Let  be given. Since
be given. Since  ,
,

there is  such that
such that

It follows form (3.17) and (3.38) that

By the sequentially fuzzy continuity of maps  and
and  , we can find some
, we can find some  such that for any
such that for any  ,
,

and

Hence by last inequality and (3.38), we get

On the other hand,

Hence by last inequality and (3.42), we obtain

Therefore it follows from (3.44), (3.40) and (3.39) that for every  ,
,

Therefore for every choice  ,
,  and
and  , we can find some
, we can find some  such that
such that  for every
for every  . This shows that
. This shows that  .
.
The proof for  proceeds similarly to that in the previous case.
proceeds similarly to that in the previous case.
It is not hard to see that  for every rational number
for every rational number  . Since
. Since  is a fuzzy sequentially continuous map, by the same reasoning as the proof of [46], the cubic function
is a fuzzy sequentially continuous map, by the same reasoning as the proof of [46], the cubic function  satisfies
satisfies  for every
for every  .
.
The following corollary is the Hyers-Ulam stability [7] of (1.5).
Corollary 3.6.
Let  be a Banach space, and let
be a Banach space, and let  be a real number. Suppose that a function
be a real number. Suppose that a function  satisfies
satisfies

for all  . Then there exists a unique cubic function
. Then there exists a unique cubic function  which satisfies (1.5) and the inequality
which satisfies (1.5) and the inequality

for all  . Moreover, if for each fixed
. Moreover, if for each fixed  the mapping
the mapping  from
from  to
to  is fuzzy sequentially continuous, then
is fuzzy sequentially continuous, then  for all
for all  .
.
Proof.
Denote  and
and  the fuzzy norms obtained as Corollary 3.3 on
the fuzzy norms obtained as Corollary 3.3 on  and
and  , respectively. This time we choose
, respectively. This time we choose  . By Theorem 3.1, there exists a unique cubic function
. By Theorem 3.1, there exists a unique cubic function  which satisfies the inequality
which satisfies the inequality

for all  . It follows that
. It follows that  . The rest of proof is an immediate consequence of Theorem 3.5.
. The rest of proof is an immediate consequence of Theorem 3.5.
References
Katsaras AK: Fuzzy topological vector spaces. II. Fuzzy Sets and Systems 1984,12(2):143-154. 10.1016/0165-0114(84)90034-4
Cheng SC, Mordeson JN: Fuzzy linear operators and fuzzy normed linear spaces. Bulletin of the Calcutta Mathematical Society 1994,86(5):429-436.
Chitra A, Subrahmanyam PV: Fuzzy sets and fixed points. Journal of Mathematical Analysis and Applications 1987,124(2):584-590. 10.1016/0022-247X(87)90016-3
Bag T, Samanta SK: Finite dimensional fuzzy normed linear spaces. Journal of Fuzzy Mathematics 2003,11(3):687-705.
Bag T, Samanta SK: Fuzzy bounded linear operators. Fuzzy Sets and Systems 2005,151(3):513-547. 10.1016/j.fss.2004.05.004
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1964:xvii+150. chapter VI
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222-224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64-66. 10.2969/jmsj/00210064
Rassias TM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297-300. 10.1090/S0002-9939-1978-0507327-1
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982,46(1):126-130. 10.1016/0022-1236(82)90048-9
Kim H-M, Rassias JM, Cho Y-S: Stability problem of Ulam for Euler-Lagrange quadratic mappings. Journal of Inequalities and Applications 2007, 2007:-15.
Rassias JM: Complete solution of the multi-dimensional problem of Ulam. Discussiones Mathematicae 1994, 14: 101-107.
Pietrzyk A: Stability of the Euler-Lagrange-Rassias functional equation. Demonstratio Mathematica 2006,39(3):523-530.
Lee Y-S, Chung S-Y: Stability of an Euler-Lagrange-Rassias equation in the spaces of generalized functions. Applied Mathematics Letters 2008,21(7):694-700. 10.1016/j.aml.2007.07.022
Rassias JM, Rassias MJ: On some approximately quadratic mappings being exactly quadratic. The Journal of the Indian Mathematical Society 2002,69(1–4):155-160.
Park C, Rassias JM: Stability of the Jensen-type functional equation in
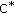 -algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.
-algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.Gordji ME, Rassias JM, Ghobadipour N: Generalized Hyers-Ulam stability of generalized (N,K)-derivations. Abstract and Applied Analysis 2009, 2009:-8.
Gordji ME, Gharetapeh SK, Rassias JM, Zolfaghari S: Solution and stability of a mixed type additive, quadratic, and cubic functional equation. Advances in Difference Equations 2009, 2009:-17.
Gordji ME, Rassias JM, Savadkouhi MB: Approximation of the quadratic and cubic functional equations in RN-spaces. European Journal of Pure and Applied Mathematics 2009,2(4):494-507.
Rassias JM: Solution of the Ulam stability problem for quartic mappings. Glasnik Matematički. Serija III 1999,34(54)(2):243-252.
Bouikhalene B, Elqorachi E, Rassias JM: The superstability of d'Alembert's functional equation on the Heisenberg group. Applied Mathematics Letters 2010,23(1):105-109. 10.1016/j.aml.2009.08.013
Savadkouhi MB, Gordji ME, Rassias JM, Ghobadipour N: Approximate ternary Jordan derivations on Banach ternary algebras. Journal of Mathematical Physics 2009,50(4):-9.
Rassias JM: Solution of a stability problem of Ulam. Discussiones Mathematicae 1992, 12: 95-103.
Rassias MJ, Rassias JM: On the Ulam stability for Euler-Lagrange type quadratic functional equations. The Australian Journal of Mathematical Analysis and Applications 2005,2(1):1-10.
Rassias JM, Rassias MJ: On the Ulam stability of Jensen and Jensen type mappings on restricted domains. Journal of Mathematical Analysis and Applications 2003,281(2):516-524. 10.1016/S0022-247X(03)00136-7
Ravi K, Arunkumar M, Rassias JM: Ulam stability for the orthogonally general Euler-Lagrange type functional equation. International Journal of Mathematics and Statistics 2008,3(8):36-46.
Gordji ME, Zolfaghari S, Rassias JM, Savadkouhi MB: Solution and stability of a mixed type cubic and quartic functional equation in quasi-Banach spaces. Abstract and Applied Analysis 2009, 2009:-14.
Gordji ME, Khodaei H: On the generalized Hyers-Ulam-Rassias stability of quadratic functional equations. Abstract and Applied Analysis 2009, 2009:-11.
Cao H-X, Lv J-R, Rassias JM: Superstability for generalized module left derivations and generalized module derivations on a Banach module (I). Journal of Inequalities and Applications 2009, 2009:-10.
Cao H-X, Lv J-R, Rassias JM: Superstability for generalized module left derivations and generalized module derivations on a Banach module (II). Journal of Inequalities in Pure and Applied Mathematics 2009,10(3, article 85):1-8.
Gavruta P: An answer to a question of John M. Rassias concerning the stability of Cauchy equation. Advances in Equations and Inequalities, Hadronic Mathematic Series 1999, 67-71.
Nakmahachalasint P: On the generalized Ulam-Gavruta-Rassias stability of mixed-type linear and Euler-Lagrange-Rassias functional equations. International Journal of Mathematics and Mathematical Sciences 2007, 2007:-10.
Jun K-W, Kim H-M, Rassias JM: Extended Hyers-Ulam stability for Cauchy-Jensen mappings. Journal of Difference Equations and Applications 2007,13(12):1139-1153. 10.1080/10236190701464590
Faĭziev V, Rassias JM: Stability of generalized additive equations on Banach spaces and groups. Journal of Nonlinear Functional Analysis and Differential Equations 2007,1(2):153-173.
Rassias JM, Lee J, Kim HM: Refined Hyers-Ulam stability for Jensen type mappings. Journal of the Chungcheong Mathematical Society 2009,22(1):101-116.
Ravi K, Arunkumar M: On the Ulam-Gavruta-Rassias stability of the orthogonally Euler-Lagrange type functional equation. International Journal of Applied Mathematics & Statistics 2007,7(7):143-156.
Nakmahachalasint P: Hyers-Ulam-Rassias and Ulam-Gavruta-Rassias stabilities of an additive functional equation in several variables. International Journal of Mathematics and Mathematical Sciences 2007, 2007:-6.
SiBaha MAit, Bouikhalene B, Elqorachi E: Ulam-Gavruta-Rassias stability of a linear functional equation. International Journal of Applied Mathematics & Statistics 2007,7(7):157-166.
Belaid B, Elqorachi E: Ulam-G\u avruta-Rassias stability of the Pexider functional equation. International Journal of Applied Mathematics & Statistics 2007,7(7):27-39.
Ravi K, Rassias JM, Arunkumar M, Kodandan R: Stability of a generalized mixed type additive, quadratic, cubic and quartic functional equation. Journal of Inequalities in Pure and Applied Mathematics 2009,10(4, article 114):1-29.
Kramosil I, Michálek J: Fuzzy metrics and statistical metric spaces. Kybernetika 1975,11(5):336-344.
Felbin C: Finite-dimensional fuzzy normed linear space. Fuzzy Sets and Systems 1992,48(2):239-248. 10.1016/0165-0114(92)90338-5
Subrahmanyam PV: A common fixed point theorem in fuzzy metric spaces. Information Sciences 1995,83(3-4):109-112. 10.1016/0020-0255(94)00043-B
Xiao J, Zhu X: Topological degree theory and fixed point theorems in fuzzy normed space. Fuzzy Sets and Systems 2004,147(3):437-452. 10.1016/j.fss.2004.01.003
Rassias JM: Solution of the Ulam stability problem for cubic mappings. Glasnik Matematički. Serija III 2001,36(56)(1):63-72.
Mirmostafaee AK, Moslehian MS: Fuzzy approximately cubic mappings. Information Sciences 2008,178(19):3791-3798. 10.1016/j.ins.2008.05.032
Mirmostafaee AK, Moslehian MS: Fuzzy versions of Hyers-Ulam-Rassias theorem. Fuzzy Sets and Systems 2008,159(6):720-729. 10.1016/j.fss.2007.09.016
Mirmostafaee AK, Mirzavaziri M, Moslehian MS: Fuzzy stability of the Jensen functional equation. Fuzzy Sets and Systems 2008,159(6):730-738. 10.1016/j.fss.2007.07.011
Wiwatwanich A, Nakmahachalasint P: On the stability of a cubic functional equation. Thai Journal of Mathematics 2008,6(3):69-76.
Eshaghi Gordji M, Bavand Savadkouhi M: Stability of mixed type cubic and quartic functional equations in random normed spaces. Journal of Inequalities and Applications 2009, 2009:-9.
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Moslehian MS, Sadeghi G: Stability of two types of cubic functional equations in non-Archimedean spaces. Real Analysis Exchange 2008,33(2):375-383.
Eshaghi M, Kaboli-Gheretapeh S, Moslehian MS, Zolfaghari S: Stability of a mixed type additive, quadratic, cubic and quartic functional equation. In Nonlinear Analysis and Variational Problems, Springer Optimization and Its Applications, 35. Edited by: Pardalos PM, Rassias TM, Khan AA. Springer, Berlin, Germany; 2009.
Rassias TM (Ed): Functional Equations and Inequalities, Mathematics and Its Applications. Volume 518. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xii+336.
Park K-H, Jung Y-S: Stability of a cubic functional equation on groups. Bulletin of the Korean Mathematical Society 2004,41(2):347-357. 10.4134/BKMS.2004.41.2.347
Rassias JM: On the stability of the Euler-Lagrange functional equation. Chinese Journal of Mathematics 1992,20(2):185-190.
Rassias JM, Rassias MJ: Asymptotic behavior of alternative Jensen and Jensen type functional equations. Bulletin des Sciences Mathématiques 2005,129(7):545-558. 10.1016/j.bulsci.2005.02.001
Rassias JM, Kim H-M: Approximate homomorphisms and derivations between
 -ternary algebras. Journal of Mathematical Physics 2008,49(6):-10.
-ternary algebras. Journal of Mathematical Physics 2008,49(6):-10.Park C, Rassias JM: Stability of the Jensen-type functional equation in
 -algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.
-algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.Ghaffari A, Alinejad A, Eshaghi Gordji M: On the stability of general cubic-quartic functional equations in Menger probabilistic normed spaces. Journal of Mathematical Physics 2009,50(12):-7.
Bag T, Samanta SK: Product fuzzy normed linear spaces. Journal of Fuzzy Mathematics 2005,13(3):545-565.
Bag T, Samanta SK: Fixed point theorems on fuzzy normed linear spaces. Information Sciences 2006,176(19):2910-2931. 10.1016/j.ins.2005.07.013
Acknowledgments
The second author would like to thank the office of gifted students at the Semnan university for financial support.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ghaffari, A., Alinejad, A. Stabilities of Cubic Mappings in Fuzzy Normed Spaces. Adv Differ Equ 2010, 150873 (2010). https://doi.org/10.1155/2010/150873
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/150873
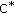 -algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.
-algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17. -ternary algebras. Journal of Mathematical Physics 2008,49(6):-10.
-ternary algebras. Journal of Mathematical Physics 2008,49(6):-10. -algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.
-algebras: a fixed point approach. Abstract and Applied Analysis 2009, 2009:-17.