- Research Article
- Open access
- Published:
Existence and Uniqueness of Mild Solution for Fractional Integrodifferential Equations
Advances in Difference Equations volume 2010, Article number: 158789 (2010)
Abstract
We study the existence and uniqueness of mild solution of a class of nonlinear fractional integrodifferential equations  ,
,  ,
,  , in a Banach space
, in a Banach space  , where
, where  . New results are obtained by fixed point theorem. An application of the abstract results is also given.
. New results are obtained by fixed point theorem. An application of the abstract results is also given.
1. Introduction
An integrodifferential equation is an equation which involves both integrals and derivatives of an unknown function. It arises in many fields like electronic, fluid dynamics, biological models, and chemical kinetics. A well-known example is the equations of basic electric circuit analysis. In recent years, the theory of various integrodifferential equations in Banach spaces has been studied deeply due to their important values in sciences and technologies, and many significant results have been established (see, e.g., [1–11] and references therein).
On the other hand, many phenomena in Engineering, Physics, Economy, Chemistry, Aerodynamics, and Electrodynamics of complex medium can be modeled by fractional differential equations. During the past decades, such problem attracted many researchers (see [1, 12–21] and references therein).
However, among the previous researches on the fractional differential equations, few are concerned with mild solutions of the fractional integrodifferential equations as follows:

where  , and the fractional derivative is understood in the Caputo sense.
, and the fractional derivative is understood in the Caputo sense.
In this paper, motivated by [1–27] (especially the estimating approaches given in [4, 6, 10, 24, 27]), we investigate the existence and uniqueness of mild solution of (1.1) in a Banach space  :
:  generates a compact semigroup
generates a compact semigroup  of uniformly bounded linear operators on a Banach space
of uniformly bounded linear operators on a Banach space  . The function
. The function  is real valued and locally integrable on
is real valued and locally integrable on  , and the nonlinear maps
, and the nonlinear maps  and
and  are defined on
are defined on  into
into  . New existence and uniqueness results are given. An example is given to show an application of the abstract results.
. New existence and uniqueness results are given. An example is given to show an application of the abstract results.
2. Preliminaries
In this paper, we set  , a compact interval in
, a compact interval in  . We denote by
. We denote by  a Banach space with norm
a Banach space with norm  . Let
. Let  be the infinitesimal generator of a compact semigroup
be the infinitesimal generator of a compact semigroup  of uniformly bounded linear operators. Then there exists
of uniformly bounded linear operators. Then there exists  such that
such that  for
for  .
.
According to [22, 23], a mild solution of (1.1) can be defined as follows.
Definition 2.1.
A continuous function  satisfying the equation
satisfying the equation

for  is called a mild solution of (1.1), where
is called a mild solution of (1.1), where

and  is a probability density function defined on
is a probability density function defined on  such that its Laplace transform is given by
such that its Laplace transform is given by

Remark 2.2.
Noting that  (cf., [23]), we can see that
(cf., [23]), we can see that

In this paper, we use  to denote the
to denote the  norm of
norm of  whenever
whenever  for some
for some  with
with  .
.  denotes the Banach space of all continuous functions
denotes the Banach space of all continuous functions  endowed with the sup-norm given by
endowed with the sup-norm given by  for
for  . Set
. Set  .
.
The following well-known theorem will be used later.
Theorem 2.3 (Krasnosel'skii).
Let  be a closed convex and nonempty subset of a Banach space
be a closed convex and nonempty subset of a Banach space  . Let
. Let  be two operators such that
be two operators such that
-
(i)
 whenever
whenever 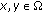 ,
, -
(ii)
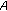 is compact and continuous,
is compact and continuous, -
(iii)
 is a contraction mapping.
is a contraction mapping.
Then there exists  such that
such that  .
.
3. Main Results
We will require the following assumptions.
(H1) The function  is continuous, and there exists
is continuous, and there exists  such that
such that

(H2) The function  ,
,  , satisfies
, satisfies

Theorem 3.1.
Let  be the infinitesimal generator of a strongly continuous semigroup
be the infinitesimal generator of a strongly continuous semigroup  with
with  ,
,  . If the maps
. If the maps  and
and  satisfy (H1),
satisfy (H1),  satisfies (H2), and
satisfies (H2), and

then (1.1) has a unique mild solution for every  .
.
Proof.
Define the mapping  by
by

Set  ,
,  .
.
Choose  such that
such that

Let  be the nonempty closed and convex set given by
be the nonempty closed and convex set given by

Then for  , we have
, we have

Noting that

we obtain

for  . Hence
. Hence  .
.
Let  and
and  be two elements in
be two elements in  . Then
. Then

So

The conclusion follows by the contraction mapping principle.
We assume the following.
(H3) The function  is continuous, and there exists a positive function
is continuous, and there exists a positive function  (
( ) such that
) such that

and set 
Let  be the infinitesimal generator of a compact semigroup
be the infinitesimal generator of a compact semigroup  of uniformly bounded linear operators. Then there exists a constant
of uniformly bounded linear operators. Then there exists a constant  such that
such that  for
for  .
.
Theorem 3.2.
If the maps  and
and  satisfy (H1), (H3), respectively, and
satisfy (H1), (H3), respectively, and

then (1.1) has a mild solution for every  .
.
Proof.
Define

Choose  such that
such that

where  .
.
Let  be the closed convex and nonempty subset of the space
be the closed convex and nonempty subset of the space  .
.
Letting  , we have
, we have

Set  .
.
According to the Hölder inequality, (H1), and (3.8), for  , we have
, we have

Thus,  .
.
For  and
and  , using (H1), we obtain
, using (H1), we obtain

So, we know that  is a contraction mapping.
is a contraction mapping.
Set  .
.
Fix  . For
. For  , set
, set

Since  is compact for each
is compact for each  , the sets
, the sets  are relatively compact in
are relatively compact in  for each
for each  ,
,  . Furthermore,
. Furthermore,

which implies that  is relatively compact in
is relatively compact in  .
.
Next, we prove that  is equicontinuous.
is equicontinuous.
For  , we have
, we have

By (H3), we get

In view of the assumption of  , we see that
, we see that  tends to 0 as
tends to 0 as  , and one
, and one

Clearly, the last term tends to  as
as  . Hence
. Hence  as
as  , and
, and

The right-hand side of (3.24) tends to  as
as  as a consequence of the continuity of
as a consequence of the continuity of  in the uniform operator topology for
in the uniform operator topology for  by the compactness of
by the compactness of  . So
. So  as
as  . Thus,
. Thus,  , as
, as  , which is independent of
, which is independent of  . Therefore
. Therefore  is compact by the Arzela-Ascoli theorem.
is compact by the Arzela-Ascoli theorem.
Next we show that  is continuous.
is continuous.
Let  be a sequence of
be a sequence of  such that
such that  in
in  . By the continuity of
. By the continuity of  on
on  , we have
, we have

Noting the continuity of  , we get
, we get

Thus, we have

So  is continuous.
is continuous.
By Krasnosel'skii's theorem, we have the conclusion of the theorem.
Remark 3.3.
In Theorem 3.2, if we furthermore suppose that the hypothesis
(H4)

holds, then we can obtain the uniqueness of the mild solution in Theorem 3.2.
Actually, from what we have just proved, (1.1) has a mild solution  and
and

Let  be another mild solution of (1.1). Then
be another mild solution of (1.1). Then

which implies by Gronwall's inequality that (1.1) has a unique mild solution  .
.
Example 3.4.
Let  . Define
. Define

Then  generates a compact, analytic semigroup
generates a compact, analytic semigroup  of uniformly bounded linear operators.
of uniformly bounded linear operators.
Let  ,
,  , and let
, and let  ,
,  be positive constants. We set
be positive constants. We set

 , and
, and  .
.
It is not hard to see that  and
and  satisfy (H1), (H3), respectively, and if
satisfy (H1), (H3), respectively, and if

then (1.1) has a unique mild solution by Theorem 3.2 and Remark 3.3.
References
El-Borai MM, Debbouche A: On some fractional integro-differential equations with analytic semigroups. International Journal of Contemporary Mathematical Sciences 2009,4(25–28):1361-1371.
Ding H-S, Liang J, Xiao T-J: Positive almost automorphic solutions for a class of non-linear delay integral equations. Applicable Analysis 2009,88(2):231-242. 10.1080/00036810802713875
Ding H-S, Xiao T-J, Liang J: Existence of positive almost automorphic solutions to nonlinear delay integral equations. Nonlinear Analysis: Theory, Methods & Applications 2009,70(6):2216-2231. 10.1016/j.na.2008.03.001
Liang J, Liu JH, Xiao T-J: Nonlocal problems for integrodifferential equations. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2008,15(6):815-824.
Liang J, Nagel R, Xiao T-J: Approximation theorems for the propagators of higher order abstract Cauchy problems. Transactions of the American Mathematical Society 2008,360(4):1723-1739. 10.1090/S0002-9947-07-04551-5
Liang J, Xiao T-J: Semilinear integrodifferential equations with nonlocal initial conditions. Computers & Mathematics with Applications 2004,47(6-7):863-875. 10.1016/S0898-1221(04)90071-5
Xiao T-J, Liang J: The Cauchy Problem for Higher-Order Abstract Differential Equations, Lecture Notes in Mathematics. Volume 1701. Springer, Berlin, Germany; 1998:xii+301.
Xiao T-J, Liang J: Approximations of Laplace transforms and integrated semigroups. Journal of Functional Analysis 2000,172(1):202-220. 10.1006/jfan.1999.3545
Xiao T-J, Liang J: Second order differential operators with Feller-Wentzell type boundary conditions. Journal of Functional Analysis 2008,254(6):1467-1486. 10.1016/j.jfa.2007.12.012
Xiao T-J, Liang J: Blow-up and global existence of solutions to integral equations with infinite delay in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e1442-e1447. 10.1016/j.na.2009.01.204
Xiao T-J, Liang J, van Casteren J: Time dependent Desch-Schappacher type perturbations of Volterra integral equations. Integral Equations and Operator Theory 2002,44(4):494-506. 10.1007/BF01193674
Hilfer R (Ed): Applications of Fractional Calculus in Physics. World Scientific, River Edge, NJ, USA; 2000:viii+463.
Henderson J, Ouahab A: Fractional functional differential inclusions with finite delay. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):2091-2105. 10.1016/j.na.2008.02.111
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2677-2682. 10.1016/j.na.2007.08.042
Liu H, Chang J-C: Existence for a class of partial differential equations with nonlocal conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3076-3083. 10.1016/j.na.2008.04.009
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York; 1993:xvi+366.
N'Guérékata GM: A Cauchy problem for some fractional abstract differential equation with non local conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1873-1876. 10.1016/j.na.2008.02.087
Mophou GM, N'Guérékata GM: Existence of the mild solution for some fractional differential equations with nonlocal conditions. Semigroup Forum 2009,79(2):315-322. 10.1007/s00233-008-9117-x
Mophou GM, N'Guérékata GM: A note on a semilinear fractional differential equation of neutral type with infinite delay. Advances in Difference Equations 2010, 2010:-8.
Zhu X-X: A Cauchy problem for abstract fractional differential equations with infinite delay. Communications in Mathematical Analysis 2009,6(1):94-100.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons and Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
El-Borai MM: On some stochastic fractional integro-differential equations. Advances in Dynamical Systems and Applications 2006,1(1):49-57.
Liang J, van Casteren J, Xiao T-J: Nonlocal Cauchy problems for semilinear evolution equations. Nonlinear Analysis: Theory, Methods & Applications 2002,50(2):173-189. 10.1016/S0362-546X(01)00743-X
Liang J, Xiao T-J: Solvability of the Cauchy problem for infinite delay equations. Nonlinear Analysis: Theory, Methods & Applications 2004,58(3-4):271-297. 10.1016/j.na.2004.05.005
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Xiao T-J, Liang J: Existence of classical solutions to nonautonomous nonlocal parabolic problems. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):e225-e232. 10.1016/j.na.2005.02.067
Acknowledgments
The authors are grateful to the referees for their valuable suggestions. The first author is supported by the NSF of Yunnan Province (2009ZC054M).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, F., N'Guérékata, G. Existence and Uniqueness of Mild Solution for Fractional Integrodifferential Equations. Adv Differ Equ 2010, 158789 (2010). https://doi.org/10.1155/2010/158789
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/158789
 whenever
whenever 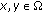 ,
,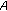 is compact and continuous,
is compact and continuous, is a contraction mapping.
is a contraction mapping.