- Research Article
- Open access
- Published:
Existence and Uniqueness of Periodic Solutions for a Class of Nonlinear Equations with 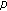 -Laplacian-Like Operators
-Laplacian-Like Operators
Advances in Difference Equations volume 2010, Article number: 197263 (2010)
Abstract
We investigate the following nonlinear equations with  -Laplacian-like operators
-Laplacian-like operators  : some criteria to guarantee the existence and uniqueness of periodic solutions of the above equation are given by using Mawhin's continuation theorem. Our results are new and extend some recent results due to Liu (B. Liu, Existence and uniqueness of periodic solutions for a kind of Lienard type
: some criteria to guarantee the existence and uniqueness of periodic solutions of the above equation are given by using Mawhin's continuation theorem. Our results are new and extend some recent results due to Liu (B. Liu, Existence and uniqueness of periodic solutions for a kind of Lienard type  -Laplacian equation, Nonlinear Analysis TMA, 69, 724–729, 2008).
-Laplacian equation, Nonlinear Analysis TMA, 69, 724–729, 2008).
1. Introduction
In this paper, we deal with the existence and uniqueness of periodic solutions for the following nonlinear equations with  -Laplacian-like operators:
-Laplacian-like operators:

where  ,
,  are continuous functions on
are continuous functions on  , and
, and  is a continuous function on
is a continuous function on  with period
with period  ; moreover,
; moreover,  is a continuous function satisfying the following:
is a continuous function satisfying the following:
(H1) for any  and
and  ;
;
(H2) there exists a function  such that
such that  and
and

It is obvious that under these two conditions,  is an homeomorphism from
is an homeomorphism from  onto
onto  and is increasing on
and is increasing on 
Recall that  -Laplacian equations have been of great interest for many mathematicians. Especially, there is a large literature (see, e.g., [1–7] and references therein) about the existence of periodic solutions to the following
-Laplacian equations have been of great interest for many mathematicians. Especially, there is a large literature (see, e.g., [1–7] and references therein) about the existence of periodic solutions to the following  -Laplacian equation:
-Laplacian equation:

and its variants, where  for
for  and
and  . Obviously, (1.3) is a special case of (1.1).
. Obviously, (1.3) is a special case of (1.1).
However, there are seldom results about the existence of periodic solutions to (1.1). The main difficulty lies in the  -Laplacian-like operator
-Laplacian-like operator  of (1.1), which is more complicated than
of (1.1), which is more complicated than  in (1.3). Since there is no concrete form for the
in (1.3). Since there is no concrete form for the  -Laplacian-like operator
-Laplacian-like operator  of (1.1), it is more difficult to prove the existence of periodic solutions to (1.1).
of (1.1), it is more difficult to prove the existence of periodic solutions to (1.1).
Therefore, in this paper, we will devote ourselves to investigate the existence of periodic solutions to (1.1). As one will see, our theorem generalizes some recent results even for the case of  (see Remark 2.2).
(see Remark 2.2).
Next, let us recall some notations and basic results. For convenience, we denote

which is a Banach space endowed with the norm  , where
, where

In the proof of our main results, we will need the following classical Mawhin's continuation theorem.
Lemma 1.1 ([8]).
Let (H1), (H2) hold and  is Carathéodory. Assume that
is Carathéodory. Assume that  is an open bounded set in
is an open bounded set in  such that the following conditions hold.
such that the following conditions hold.
(S1) For each  , the problem
, the problem

has no solution on  .
.
(S2) The equation

has no solution on 
(S3) The Brouwer degree

Then the periodic boundary value problem

has at least one  -periodic solution on
-periodic solution on  .
.
2. Main Results
In this section, we prove an existence and uniqueness theorem for (1.1).
Theorem 2.1.
Suppose the following assumptions hold:
(A1)  and
and  for all
for all  ;
;
(A2) there exist a constant  and a function
and a function  such that for all
such that for all  and
and  ,
,

Then (1.1) has a unique  -periodic solution.
-periodic solution.
Proof
Existence. For the proof of existence, we use Lemma 1.1. First, let us consider the homotopic equation of (1.1):

Let  be an arbitrary solution of (2.2). By integrating the two sides of (2.2) over
be an arbitrary solution of (2.2). By integrating the two sides of (2.2) over  , and noticing that
, and noticing that  and
and  , we have
, we have

that is,

Since  is continuous, there exists
is continuous, there exists  such that
such that

In view of (A1), we obtain

where  . Then, for each
. Then, for each  , we have
, we have

which gives that

Thus,

Since  , there is a constant
, there is a constant  such that
such that

Set

In view of (A2) and

we get

where

By (2.9), we have

Noticing that

there exists a constant  such that
such that

On the other hand, it follows from

that  for
for  . In addition, since
. In addition, since  , there exists
, there exists  such that
such that  . Thus
. Thus  .
.
Then, for all  , we have
, we have

For the above  , it follows from
, it follows from  that there exists
that there exists  such that
such that

Combining this with  , we get
, we get

which yields that  .
.
Now, we have proved that any solution  of (2.2) satisfies
of (2.2) satisfies

Since  , we have
, we have

In view of  being strictly decreasing, we get
being strictly decreasing, we get

Set

Then, we know that (2.2) has no solution on  for each
for each  , that is, the assumption (S1) of Lemma 1.1 holds. In addition, it follows from (2.24) that
, that is, the assumption (S1) of Lemma 1.1 holds. In addition, it follows from (2.24) that

So the assumption (S2) of Lemma 1.1 holds. Let

For  and
and  , by (2.24), we have
, by (2.24), we have

Thus,  is a homotopic transformation. So
is a homotopic transformation. So

that is, the assumption (S3) of Lemma 1.1 holds. By applying Lemma 1.1, there exists at least one solution with period  to (1.1).
to (1.1).
Uniqueness. Let

Then (1.1) is transformed into

Let  and
and  being two
being two  -periodic solutions of (1.1); and
-periodic solutions of (1.1); and

Then we obtain

Setting

it follows from (2.33) that

Now, we claim that

If this is not true, we consider the following two cases.
Case 1.
There exists  such that
such that

which implies that

By (A1),  . So it follows from
. So it follows from  that
that  . Thus, in view of
. Thus, in view of

and (H1), we obtain

which contradicts with  .
.
Case 2.

Also, we have  and
and  . Then, similar to the proof of Case 1, one can get a contradiction.
. Then, similar to the proof of Case 1, one can get a contradiction.
Now, we have proved that

Analogously, one can show that

So we have  . Then, it follows from (2.35) that
. Then, it follows from (2.35) that

which implies that

Hence, (1.1) has a unique  -periodic solution. The proof of Theorem 2.1 is now completed.
-periodic solution. The proof of Theorem 2.1 is now completed.
Remark 2.2.
In Theorem 2.1, setting  , then (A2) becomes as follows:
, then (A2) becomes as follows:
(A2′) there exists a constant  such that for all
such that for all  and
and  ,
,

In the case  , Liu [7, Theorem
, Liu [7, Theorem  ] proved that (1.1) has a unique
] proved that (1.1) has a unique  -periodic solution under the assumptions (A1) and (
-periodic solution under the assumptions (A1) and ( ). Thus, even for the case of
). Thus, even for the case of  , Theorem 2.1 is a generalization of [7, Theorem 1].
, Theorem 2.1 is a generalization of [7, Theorem 1].
In addition, we have the following interesting corollary.
Corollary 2.3.
Suppose (A1) and
(A2″) there exist a constant  such that
such that

hold. Then (1.1) has a unique  -periodic solution.
-periodic solution.
Proof.
Let  . Noticing that
. Noticing that

we know that (A2) holds with  . This completes the proof.
. This completes the proof.
At last, we give two examples to illustrate our results.
Example 2.4.
Consider the following nonlinear equation:

where  ,
,  ,
,  , and
, and  . One can easily check that
. One can easily check that  satisfy (H1) and (H2). Obviously, (A1) holds. Moreover, since
satisfy (H1) and (H2). Obviously, (A1) holds. Moreover, since

it is easy to verify that (A2) holds. By Theorem 2.1, (2.49) has a unique  -periodic solution.
-periodic solution.
Example 2.5.
Consider the following  -Laplacian equation:
-Laplacian equation:

where  , and
, and  . Obviously, (A1) holds. Moreover, we have
. Obviously, (A1) holds. Moreover, we have

So ( ) holds. Then, by Corollary 2.3, (2.51) has a unique
) holds. Then, by Corollary 2.3, (2.51) has a unique  -periodic solution.
-periodic solution.
Remark 2.6.
In Example 2.5,  , we have
, we have

Thus, ( ) does not hold. So [7, Theorem 1] cannot be applied to Example 2.5. This means that our results generalize [7, Theorem 1] in essence even for the case of
) does not hold. So [7, Theorem 1] cannot be applied to Example 2.5. This means that our results generalize [7, Theorem 1] in essence even for the case of  .
.
References
Lu S: New results on the existence of periodic solutions to a
 -Laplacian differential equation with a deviating argument. Journal of Mathematical Analysis and Applications 2007,336(2):1107-1123. 10.1016/j.jmaa.2007.03.032
-Laplacian differential equation with a deviating argument. Journal of Mathematical Analysis and Applications 2007,336(2):1107-1123. 10.1016/j.jmaa.2007.03.032Lu S:Existence of periodic solutions to a
 -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041Liu B:Periodic solutions for Liénard type
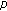 -Laplacian equation with a deviating argument. Journal of Computational and Applied Mathematics 2008,214(1):13-18. 10.1016/j.cam.2007.02.004
-Laplacian equation with a deviating argument. Journal of Computational and Applied Mathematics 2008,214(1):13-18. 10.1016/j.cam.2007.02.004Cheung W-S, Ren J:Periodic solutions for
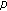 -Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.
-Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.Cheung W-S, Ren J:Periodic solutions for
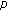 -Laplacian differential equation with multiple deviating arguments. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):727-742. 10.1016/j.na.2005.03.096
-Laplacian differential equation with multiple deviating arguments. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):727-742. 10.1016/j.na.2005.03.096Cheung W-S, Ren J:Periodic solutions for
 -Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002
-Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002Liu B:Existence and uniqueness of periodic solutions for a kind of Liénard type
 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007Manásevich R, Mawhin J:Periodic solutions for nonlinear systems with
 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
Acknowledgments
The authors are grateful to the referee for valuable suggestions and comments, which improved the quality of this paper. The work was supported by the NSF of China, the NSF of Jiangxi Province of China (2008GQS0057), the Youth Foundation of Jiangxi Provincial Education Department (GJJ09456), and the Youth Foundation of Jiangxi Normal University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ding, HS., Ye, GR. & Long, W. Existence and Uniqueness of Periodic Solutions for a Class of Nonlinear Equations with 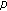 -Laplacian-Like Operators.
Adv Differ Equ 2010, 197263 (2010). https://doi.org/10.1155/2010/197263
-Laplacian-Like Operators.
Adv Differ Equ 2010, 197263 (2010). https://doi.org/10.1155/2010/197263
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/197263
 -Laplacian differential equation with a deviating argument. Journal of Mathematical Analysis and Applications 2007,336(2):1107-1123. 10.1016/j.jmaa.2007.03.032
-Laplacian differential equation with a deviating argument. Journal of Mathematical Analysis and Applications 2007,336(2):1107-1123. 10.1016/j.jmaa.2007.03.032 -Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041
-Laplacian Liénard differential equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2008,68(6):1453-1461. 10.1016/j.na.2006.12.041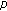 -Laplacian equation with a deviating argument. Journal of Computational and Applied Mathematics 2008,214(1):13-18. 10.1016/j.cam.2007.02.004
-Laplacian equation with a deviating argument. Journal of Computational and Applied Mathematics 2008,214(1):13-18. 10.1016/j.cam.2007.02.004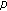 -Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.
-Laplacian Liénard equation with a deviating argument. Nonlinear Analysis: Theory, Methods & Applications 2004,59(1-2):107-120.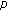 -Laplacian differential equation with multiple deviating arguments. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):727-742. 10.1016/j.na.2005.03.096
-Laplacian differential equation with multiple deviating arguments. Nonlinear Analysis: Theory, Methods & Applications 2005,62(4):727-742. 10.1016/j.na.2005.03.096 -Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002
-Laplacian Rayleigh equations. Nonlinear Analysis: Theory, Methods & Applications 2006,65(10):2003-2012. 10.1016/j.na.2005.11.002 -Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007
-Laplacian equation. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):724-729. 10.1016/j.na.2007.06.007 -Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425
-Laplacian-like operators. Journal of Differential Equations 1998,145(2):367-393. 10.1006/jdeq.1998.3425