- Research Article
- Open access
- Published:
Note on the Persistent Property of a Discrete Lotka-Volterra Competitive System with Delays and Feedback Controls
Advances in Difference Equations volume 2010, Article number: 249364 (2010)
Abstract
A nonautonomous  -species discrete Lotka-Volterra competitive system with delays and feedback controls is considered in this work. Sufficient conditions on the coefficients are given to guarantee that all the species are permanent. It is shown that these conditions are weaker than those of Liao et al. 2008.
-species discrete Lotka-Volterra competitive system with delays and feedback controls is considered in this work. Sufficient conditions on the coefficients are given to guarantee that all the species are permanent. It is shown that these conditions are weaker than those of Liao et al. 2008.
1. Introduction
Traditional Lotka-Volterra competitive systems have been extensively studied by many authors [1–7].The autonomous model can be expressed as follows:

where  ,
,  ,
,  ,
,  denoting the density of the i th species at time
denoting the density of the i th species at time  . Montes de Oca and Zeeman [6] investigated the general nonautonomous
. Montes de Oca and Zeeman [6] investigated the general nonautonomous  -species Lotka-Volterra competitive system
-species Lotka-Volterra competitive system

and obtained that if the coefficients are continuous and bounded above and below by positive constants, and if for each  there exists an integer
there exists an integer  such that
such that

then  exponentially for
exponentially for  and
and  where
where  is a certain solution of a logistic equation. Teng [8] and Ahmad and Stamova [9] also studied the coexistence on a nonautonomous Lotka-Volterra competitive system. They obtained the necessary or sufficient conditions for the permanence and the extinction. For more works relevant to system (1.1), one could refer to [1–9] and the references cited therein.
is a certain solution of a logistic equation. Teng [8] and Ahmad and Stamova [9] also studied the coexistence on a nonautonomous Lotka-Volterra competitive system. They obtained the necessary or sufficient conditions for the permanence and the extinction. For more works relevant to system (1.1), one could refer to [1–9] and the references cited therein.
However, to the best of the authors' knowledge, to this day, still less scholars consider the general nonautonomous discrete Lotka-Volterra competitive system with delays and feedback controls. Recently, in [1] Liao et al. considered the following general nonautonomous discrete Lotka-Volterra competitive system with delays and feedback controls:

where  is the density of competitive species;
is the density of competitive species;  is the control variable;
is the control variable;  ; bounded sequences
; bounded sequences  ,
,  ,
,  ,
,  , and
, and  ;
;  and
and  are positive integer;
are positive integer;  denote the sets of all integers and all positive real numbers, respectively;
denote the sets of all integers and all positive real numbers, respectively;  is the first-order forward difference operator
is the first-order forward difference operator  ;
;  .
.
In [1], Liao et al. obtained sufficient conditions for permanence of the system (1.4).
They obtained what follows.
Lemma 1.1.
Assume that

hold, then system (1.4) is permanent, where

Since

Hence, the above inequality (1.5) implies

That is

It was shown that in [1] Liao et al. considered system (1.4) where all coefficients  ,
,  ,
,  ,
,  ,
,  , and
, and  were assumed to satisfy conditions (1.9).
were assumed to satisfy conditions (1.9).
In this work, we shall study system (1.4) and get the same results as [1] do under the weaker assumption that

Our main results are the following Theorem 1.2.
Theorem 1.2.
Assume that (1.10) holds, then system (1.4) is permanent.
Remark 1.3.
The inequality (1.9) implies (1.10), but not conversely, for

Therefore, we have improved the permanence conditions of [1] for system (1.4).
Theorem 1.2 will be proved in Section 2. In Section 3, an example will be given to illustrate that (1.10) does not imply (1.9); that is, the condition (1.10) is better than (1.9).
2. Proof of Theorem 1.2
The following lemma can be found in [10].
Lemma 2.1.
Assume that  and
and  , and further suppose that
, and further suppose that
-
(1)
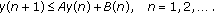 (2.1)
(2.1)
Then for any integer 

Especially, if  and
and  is bounded above with respect to
is bounded above with respect to  , then
, then



Then for any integer 

Especially, if  and
and  is bounded below with respect to
is bounded below with respect to  , then
, then

Following comparison theorem of difference equation is Theorem  of [11, page 241].
of [11, page 241].
Lemma 2.2.
Let  ,
,  For any fixed
For any fixed  is a nondecreasing function with respect to
is a nondecreasing function with respect to  , and for
, and for  , following inequalities hold:
, following inequalities hold:  ,
,  If
If  , then
, then  for all
for all  .
.
Now let us consider the following single species discrete model:

where  and
and  are strictly positive sequences of real numbers defined for
are strictly positive sequences of real numbers defined for  and
and  ,
,  Similarly to the proof of Propositions
Similarly to the proof of Propositions  and
and  in [12], we can obtain the following.
in [12], we can obtain the following.
Lemma 2.3.
Any solution of system (2.7) with initial condition  satisfies
satisfies

where

The following lemma is direct conclusion of [1].
Lemma 2.4.
Let  denote any positive solution of system (1.4).Then there exist positive constants
denote any positive solution of system (1.4).Then there exist positive constants  such that
such that

where

Proposition 2.5.
Suppose assumption (1.10) holds, then there exist positive constant  and
and  such that
such that

Proof.
We first prove  .
.
By Lemma 2.4 and by the first equation of system (1.4), we have

for  sufficiently large, then
sufficiently large, then

Thus

where

From the second equation of system (1.4), we have

Then, Lemma 2.1 implies that for any  ,
,

where

For any small positive constant  , there exists a
, there exists a  such that
such that

From the first equation of system (1.4), (2.18), and (2.20), we have

By Lemmas 2.2 and 2.3, we have

Setting  in (2.22) leads to
in (2.22) leads to

Thus,

where

Second, we prove  . For enough small
. For enough small  , from the second equation of system (1.4), we have
, from the second equation of system (1.4), we have

for sufficient large  . Hence
. Hence

Thus, we obtain

This completes the proof.
3. An Example
In this section, we give an example to illustrate that (1.10) does not imply (1.9). Consider the two-species system with delays and feedback controls for 

We have

So

Therefore (1.10) holds.
But

Thus (1.9) does not hold.
References
Liao X, Ouyang Z, Zhou S: Permanence of species in nonautonomous discrete Lotka-Volterra competitive system with delays and feedback controls. Journal of Computational and Applied Mathematics 2008,211(1):1-10. 10.1016/j.cam.2006.10.084
Ahmad S: On the nonautonomous Volterra-Lotka competition equations. Proceedings of the American Mathematical Society 1993,117(1):199-204. 10.1090/S0002-9939-1993-1143013-3
Ahmad S, Lazer AC: On the nonautonomous
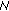 -competing species problems. Applicable Analysis 1995,57(3-4):309-323. 10.1080/00036819508840353
-competing species problems. Applicable Analysis 1995,57(3-4):309-323. 10.1080/00036819508840353Gopalsamy K: Stability and Oscillations in Delay Differential Equations of Population Dynamics, Mathematics and Its Applications. Volume 74. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1992:xii+501.
Kaykobad M: Positive solutions of positive linear systems. Linear Algebra and Its Applications 1985, 64: 133-140. 10.1016/0024-3795(85)90271-X
Montes de Oca F, Zeeman ML: Extinction in nonautonomous competitive Lotka-Volterra systems. Proceedings of the American Mathematical Society 1996,124(12):3677-3687. 10.1090/S0002-9939-96-03355-2
Zeeman ML: Extinction in competitive Lotka-Volterra systems. Proceedings of the American Mathematical Society 1995,123(1):87-96. 10.1090/S0002-9939-1995-1264833-2
Teng ZD: Permanence and extinction in nonautonomous Lotka-Volterra competitive systems with delays. Acta Mathematica Sinica 2001,44(2):293-306.
Ahmad S, Stamova IM: Almost necessary and sufficient conditions for survival of species. Nonlinear Analysis. Real World Applications 2004,5(1):219-229. 10.1016/S1468-1218(03)00037-3
Fan Y-H, Wang L-L: Permanence for a discrete model with feedback control and delay. Discrete Dynamics in Nature and Society 2008, 2008:-8.
Wang L, Wang MQ: Ordinary Difference Equation. Xinjiang University Press; 1991.
Chen F: Permanence and global attractivity of a discrete multispecies Lotka-Volterra competition predator-prey systems. Applied Mathematics and Computation 2006,182(1):3-12. 10.1016/j.amc.2006.03.026
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kong, X., Chen, L. & Yang, W. Note on the Persistent Property of a Discrete Lotka-Volterra Competitive System with Delays and Feedback Controls. Adv Differ Equ 2010, 249364 (2010). https://doi.org/10.1155/2010/249364
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/249364
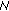 -competing species problems. Applicable Analysis 1995,57(3-4):309-323. 10.1080/00036819508840353
-competing species problems. Applicable Analysis 1995,57(3-4):309-323. 10.1080/00036819508840353