- Research Article
- Open access
- Published:
Positive and Dead-Core Solutions of Two-Point Singular Boundary Value Problems with ϕ-Laplacian
Advances in Difference Equations volume 2010, Article number: 262854 (2010)
Abstract
The paper discusses the existence of positive solutions, dead-core solutions, and pseudo-dead-core solutions of the singular problem  ,
,  ,
,  . Here
. Here  is a positive parameter,
is a positive parameter,  ,
,  ,
,  ,
,  ,
,  is singular at
is singular at  and
and  may be singular at
may be singular at  .
.
1. Introduction
Consider the singular boundary value problem


depending on the parameter  . Here
. Here  ,
,  satisfies the Carathéodory conditions on
satisfies the Carathéodory conditions on 
 ,
,  (
( ,
,  is positive,
is positive,  for a.e.
for a.e.  and each
and each  , and
, and  may be singular at
may be singular at  .
.
Throughout the paper  denotes the set of absolutely continuous functions on
denotes the set of absolutely continuous functions on  and
and  is the norm in
is the norm in  .
.
We investigate positive, dead-core, and pseudo-dead-core solutions of problem (1.1), (1.2).
A function  is a positive solution of problem (1.1), (1.2) if
is a positive solution of problem (1.1), (1.2) if  ,
,  on
on  ,
,  satisfies (1.2), and (1.1) holds for a.e.
satisfies (1.2), and (1.1) holds for a.e.  .
.
We say that  satisfying (1.2) is a dead-core solution of problem (1.1), (1.2) if there exist
satisfying (1.2) is a dead-core solution of problem (1.1), (1.2) if there exist  such that
such that  on
on  ,
,  on
on  ,
,  and (1.1) holds for a.e.
and (1.1) holds for a.e.  . The interval
. The interval  is called the dead-core of
is called the dead-core of . If
. If  , then
, then  is called a pseudo-dead-core solution of problem (1.1), (1.2).
is called a pseudo-dead-core solution of problem (1.1), (1.2).
The existence of positive and dead core solutions of singular second-order differential equations with a parameter was discussed for Dirichlet boundary conditions in [1, 2] and for mixed and Robin boundary conditions in [3–5]. Papers [6, 7] discuss also the existence and multiplicity of positive and dead core solutions of the singular differential equation  satisfying the boundary conditions
satisfying the boundary conditions  ,
,  and
and  ,
,  , respectively, and present numerical solutions. These problems are mathematical models for steady-state diffusion and reactions of several chemical species (see, e.g., [4, 5, 8, 9]). Positive and dead-core solutions to the third-order singular differential equation
, respectively, and present numerical solutions. These problems are mathematical models for steady-state diffusion and reactions of several chemical species (see, e.g., [4, 5, 8, 9]). Positive and dead-core solutions to the third-order singular differential equation

satisfying the nonlocal boundary conditions  ,
,  , were investigated in [10].
, were investigated in [10].
We work with the following conditions on the functions  and
and  in the differential equation (1.1). Without loss of generality we can assume that
in the differential equation (1.1). Without loss of generality we can assume that  for each
for each  (otherwise
(otherwise  is replaced by
is replaced by  ), where
), where  is from (1.2).
is from (1.2).
-
(H1)
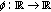 is an increasing and odd homeomorphism such that
is an increasing and odd homeomorphism such that  .
. -
(H2)
 , where
, where  , and
, and (1.4)
(1.4) -
(H3)for a.e.
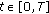 and all
and all  ,
,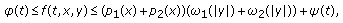 (1.5)
(1.5)
where  ,
,  ,
,  ,
,  , and
, and  are positive,
are positive,  are nonincreasing,
are nonincreasing,  are nondecreasing,
are nondecreasing,  for
for  , and
, and

The aim of this paper is to discuss the existence of positive, dead-core, and pseudo-dead-core solutions of problem (1.1), (1.2). Since problem (1.1), (1.2) is singular we use regularization and sequential techniques.
For this end for  , we define
, we define 
 , where
, where  , and
, and  by the formulas
by the formulas

Then  and
and  give
give




Consider the auxiliary regular differential equation

A function  is a solution of problem (1.12), (1.2) if
is a solution of problem (1.12), (1.2) if  ,
,  fulfils (1.2), and (1.12) holds for a.e.
fulfils (1.2), and (1.12) holds for a.e.  .
.
We introduce also the notion of a sequential solution of problem (1.1), (1.2). We say that  is a sequential solution of problem (1.1), (1.2) if there exists a sequence
is a sequential solution of problem (1.1), (1.2) if there exists a sequence  ,
,  , such that
, such that  in
in  , where
, where  is a solution of problem (1.12), (1.2) with
is a solution of problem (1.12), (1.2) with  replaced by
replaced by  . In Section 3 (see Theorem 3.1) we show that any sequential solution of problem (1.1), (1.2) is either a positive solution or a pseudo-dead-core solution or a dead-core solution of this problem.
. In Section 3 (see Theorem 3.1) we show that any sequential solution of problem (1.1), (1.2) is either a positive solution or a pseudo-dead-core solution or a dead-core solution of this problem.
The next part of our paper is divided into two sections. Section 2 is devoted to the auxiliary regular problem (1.12), (1.2). We prove the solvability of this problem by the existence principle in [11] and investigate the properties of solutions. The main results are given in Section 3. We prove that under assumptions ( )–(
)–( ), for each
), for each  problem (1.1), (1.2) has a sequential solution and that any sequential solution is either a positive solution or a pseudo-dead-core solution or a dead-core solution (Theorem 3.1). Theorem 3.2 shows that for sufficiently small values of
problem (1.1), (1.2) has a sequential solution and that any sequential solution is either a positive solution or a pseudo-dead-core solution or a dead-core solution (Theorem 3.1). Theorem 3.2 shows that for sufficiently small values of  all sequential solutions of problem (1.1), (1.2) are positive solutions while, by Theorem 3.3, all sequential solutions are dead-core solutions if
all sequential solutions of problem (1.1), (1.2) are positive solutions while, by Theorem 3.3, all sequential solutions are dead-core solutions if  is sufficiently large. An example demonstrates the application of our results.
is sufficiently large. An example demonstrates the application of our results.
2. Auxiliary Regular Problems
The properties of solutions of problem (1.12), (1.2) are given in the following lemma.
Lemma 2.1.
Let ( )–(
)–( ) hold. Let
) hold. Let  be a solution of problem (1.12), (1.2). Then
be a solution of problem (1.12), (1.2). Then



Proof.
Suppose that  . Then
. Then  . Let
. Let

Then  and, by (1.9),
and, by (1.9),  a.e. on
a.e. on  . Hence
. Hence  is increasing on
is increasing on  , and therefore,
, and therefore,  is also increasing on this interval since
is also increasing on this interval since  is increasing on
is increasing on  by
by  . Consequently,
. Consequently,  and
and  on
on  . Then
. Then  , which contradicts
, which contradicts  . Hence
. Hence  . Let
. Let  . Then
. Then  on a right neighbourhood of
on a right neighbourhood of  . Put
. Put

Then  on
on  , and therefore,
, and therefore,  a.e. on
a.e. on  , which implies that
, which implies that  is decreasing on
is decreasing on  . Now it follows from
. Now it follows from  and
and  that
that  ,
,  on
on  and
and  on
on  . Consequently,
. Consequently,  , which contradicts
, which contradicts  . To summarize,
. To summarize,  and
and  . Suppose that
. Suppose that  . Then there exist
. Then there exist  such that
such that  ,
,  and
and  on
on  . Hence
. Hence  a.e. on
a.e. on  and arguing as in the above part of the proof we can verify that
and arguing as in the above part of the proof we can verify that  and
and  ,
,  on
on  . Consequently,
. Consequently,  , which is impossible. Hence
, which is impossible. Hence  on
on  . New it follows from (1.9) and (1.10) that
. New it follows from (1.9) and (1.10) that  a.e. on
a.e. on  , which together with
, which together with  gives that
gives that  is nondecreasing on
is nondecreasing on  . Suppose that
. Suppose that  for some
for some  . If
. If  , then
, then  , which contradicts
, which contradicts  since
since  . Hence
. Hence  and
and  . Let
. Let

Then  ,
,  and
and  is increasing on
is increasing on  since
since  a.e. on this interval by (1.9). Hence there exists
a.e. on this interval by (1.9). Hence there exists  ,
,  , such that
, such that  on
on  and it follows from the definition of the function
and it follows from the definition of the function  that
that

where  ,
,  and
and  a.e. on
a.e. on  . Integrating (2.7) over
. Integrating (2.7) over  yields
yields

From this equality, from  and from
and from  , where
, where  , we obtain
, we obtain

for  . Since
. Since  for
for  , we have
, we have

which is impossible. We have proved that

Hence  a.e. on
a.e. on  by (1.9), and therefore,
by (1.9), and therefore,  is increasing on
is increasing on  . If
. If  , then
, then  on
on  , and so
, and so  , which is impossible since
, which is impossible since  . Consequently,
. Consequently,  and
and  vanishes at a unique point
vanishes at a unique point  . Hence (2.3) is true.
. Hence (2.3) is true.
Next, we deduce from  ,
,  and from
and from  that
that  and
and  . Consequently,
. Consequently,  . Hence (2.2) holds. Inequality (2.1) follows from (2.2), (2.3), and (2.11).
. Hence (2.2) holds. Inequality (2.1) follows from (2.2), (2.3), and (2.11).
Remark 2.2.
Let  be a solution of problem (1.12), (1.2) with
be a solution of problem (1.12), (1.2) with  . Then
. Then  a.e. on
a.e. on  , and so
, and so  is a constant function. Let
is a constant function. Let  . Now, it follows from (1.2) that
. Now, it follows from (1.2) that  and
and  . Consequently,
. Consequently,  , and since
, and since  , we have
, we have  . Hence
. Hence  , and
, and  is the unique solution of problem (1.12), (1.2) for
is the unique solution of problem (1.12), (1.2) for  .
.
The following lemma gives a priori bounds for solutions of problem (1.12), (1.2).
Lemma 2.3.
Let ( )–(
)–( ) hold. Then there exists a positive constant
) hold. Then there exists a positive constant  independent of
independent of 
 and depending on
and depending on  such that
such that

for any solution  of problem (1.12), (1.2).
of problem (1.12), (1.2).
Proof.
Let  be a solution of problem (1.12), (1.2). By Lemma 2.1,
be a solution of problem (1.12), (1.2). By Lemma 2.1,  satisfies (2.1)–(2.3). Hence
satisfies (2.1)–(2.3). Hence

In view of (1.11),

for a.e.  and
and

for a.e.  . Since
. Since  for
for  by
by  , we have
, we have

Therefore,

for a.e.  and
and

for a.e.  . Integrating (2.17) over
. Integrating (2.17) over  and (2.18) over
and (2.18) over  gives
gives


respectively. We now show that condition (1.6) implies

Since  by
by  , we have
, we have  . Therefore, there exists
. Therefore, there exists  such that
such that

Then

and (2.21) follows from (1.6). Since  , inequality (2.21) guarantees the existence of a positive constant
, inequality (2.21) guarantees the existence of a positive constant  such that
such that

for all  . Hence (2.19) and (2.20) imply
. Hence (2.19) and (2.20) imply  . Consequently,
. Consequently,  and equality (2.13) shows that (2.12) is true for
and equality (2.13) shows that (2.12) is true for  .
.
Remark 2.4.
By Lemma 2.3, estimate (2.12) is true for any solution  of problem (1.12), (1.2), where
of problem (1.12), (1.2), where  is a positive constant independent of
is a positive constant independent of  and depending on
and depending on  . Fix
. Fix  and consider the differential equation
and consider the differential equation

It follows from the proof of Lemma 2.3 that  for each
for each  and any solution
and any solution  of problem (2.25), (1.2). Since
of problem (2.25), (1.2). Since  is the unique solution of this problem with
is the unique solution of this problem with  by Remark 2.2, we have
by Remark 2.2, we have  for each
for each  and any solution
and any solution  of problem (2.25), (1.2).
of problem (2.25), (1.2).
We are now in the position to show that problem (1.12), (1.2) has a solution. Let  ,
,  , be defined by
, be defined by

where  and
and  are as in (1.2). We say that the functionals
are as in (1.2). We say that the functionals  and
and  are compatible if for each
are compatible if for each  the system
the system

has a solution  . We apply the following existence principle which follows from [11–13] to prove the solvability of problem (1.12), (1.2).
. We apply the following existence principle which follows from [11–13] to prove the solvability of problem (1.12), (1.2).
Proposition 2.5.
Let ( )–(
)–( ) hold. Let there exist positive constants
) hold. Let there exist positive constants  such that
such that

for each  and any solution
and any solution  of problem (2.25), (1.2). Also assume that
of problem (2.25), (1.2). Also assume that  and
and  are compatible and there exist positive constants
are compatible and there exist positive constants  such that
such that

for each  and each solution
and each solution  of system (2.27).
of system (2.27).
Then problem (1.12), (1.2) has a solution.
Lemma 2.6.
Let ( )–(
)–( ) hold. Then problem (1.12), (1.2) has a solution.
) hold. Then problem (1.12), (1.2) has a solution.
Proof.
By Lemmas 2.1 and 2.3 and Remark 2.4, there exists a positive constant  such that
such that

for each  and any solution
and any solution  of problem (2.25), (1.2). Hence (2.28) is true for
of problem (2.25), (1.2). Hence (2.28) is true for  and
and  . System (2.27) has the form of
. System (2.27) has the form of

Subtracting the first equation from the second, we get  . Due to
. Due to  for
for  , we have
, we have  , and consequently,
, and consequently,  . Hence
. Hence  is the unique solution of system (2.31). Therefore,
is the unique solution of system (2.31). Therefore,  and
and  are compatible and (2.29) is fulfilled for
are compatible and (2.29) is fulfilled for  and
and  . The result now follows from Proposition 2.5.
. The result now follows from Proposition 2.5.
The following result deals with the sequences of solutions of problem (1.12), (1.2).
Lemma 2.7.
Let ( )–(
)–( ) hold and let
) hold and let  be a solution of problem (1.12), (1.2). Then
be a solution of problem (1.12), (1.2). Then  is equicontinuous on
is equicontinuous on  .
.
Proof.
By Lemmas 2.1 and 2.3, relations (2.1)–(2.3) and (2.12) hold, where  is a positive constant. Let
is a positive constant. Let  ,
,  and
and  be defined by the formulas
be defined by the formulas

where  and
and  are given in (1.11). Then
are given in (1.11). Then  is an increasing and odd function on
is an increasing and odd function on  ,
,  by (2.21), and
by (2.21), and  is increasing on
is increasing on  . Since
. Since  is bounded in
is bounded in  ,
,  is equicontinuous on
is equicontinuous on  , and consequently,
, and consequently,  is equicontinuous on
is equicontinuous on  , too. Let us choose an arbitrary
, too. Let us choose an arbitrary  . Then there exists
. Then there exists  such that
such that

In order to prove that  is equicontinuous on
is equicontinuous on  , let
, let  and
and  . If
. If  , then integrating (2.17) from
, then integrating (2.17) from  to
to  gives
gives

If  , then integrating (2.18) over
, then integrating (2.18) over  yields
yields

Finally, if  , then one can check that
, then one can check that

To summarize, we have

whenever  and
and  . Hence
. Hence  is equicontinuous on
is equicontinuous on  and, since
and, since  is bounded in
is bounded in  and
and  is continuous and increasing on
is continuous and increasing on  ,
,  is equicontinuous on
is equicontinuous on  .
.
The results of the following two lemmas we use in the proofs of the existence of positive and dead-core solutions to problem (1.1), (1.2).
Lemma 2.8.
Let ( )–(
)–( ) hold. Then there exist
) hold. Then there exist  and
and  such that
such that

where  is any solution of problem (1.12), (1.2) with
is any solution of problem (1.12), (1.2) with  .
.
Proof.
Suppose that the lemma was false. Then we could find sequences  and
and  ,
,  , and a solution
, and a solution  of the equation
of the equation  satisfying (1.2) such that
satisfying (1.2) such that  , where
, where  . Note that
. Note that  on
on  ,
,  on
on  ,
,  and
and  on
on  for each
for each  by Lemma 2.1. Then, by (1.11),
by Lemma 2.1. Then, by (1.11),

for a.e.  ,
,

for a.e.  , and (cf. (2.13))
, and (cf. (2.13))

Essentially, the same reasoning as in the proof of Lemma 2.3 gives that for  (cf. (2.19) and (2.20))
(cf. (2.19) and (2.20))

In view of  , we have
, we have  ,
,  . Consequently,
. Consequently,  by (2.41). We now deduce from
by (2.41). We now deduce from  for
for  and
and  , and from
, and from  that
that  . Hence
. Hence  ,
,  , which contradicts
, which contradicts  ,
,  for
for  .
.
Lemma 2.9.
Let ( )–(
)–( ) hold. Then for each
) hold. Then for each  there exists
there exists  such that
such that

where  is any solution of problem (1.12), (1.2) with
is any solution of problem (1.12), (1.2) with  .
.
Proof.
Fix  and let
and let  be as in
be as in  . Put
. Put  ,
,

Let  and choose
and choose  . If we prove that
. If we prove that

where  is any solution of problem (1.12), (1.2), then (2.43) is true since
is any solution of problem (1.12), (1.2), then (2.43) is true since  by Lemma 2.1. In order to prove (2.45), suppose the contrary, that is suppose that there is some
by Lemma 2.1. In order to prove (2.45), suppose the contrary, that is suppose that there is some  such that
such that  . The next part of the proof is broken into two cases if
. The next part of the proof is broken into two cases if  or
or  .
.
Case 1.
Suppose  . By Lemma 2.1,
. By Lemma 2.1,  is increasing on
is increasing on  . Consequently, if
. Consequently, if  , then
, then  for
for  , and so
, and so

which contradicts  by Lemma 2.1. Therefore,
by Lemma 2.1. Therefore,

Keeping in mind that  for
for  , we have, by (1.8),
, we have, by (1.8),

and therefore,

Then

which yields

Hence  , which contradicts the first inequality in (2.47).
, which contradicts the first inequality in (2.47).
Case 2.
Suppose  . Then
. Then  is positive and increasing on
is positive and increasing on  by Lemma 2.1. If
by Lemma 2.1. If  , then
, then  on
on  , and consequently,
, and consequently,

which contradicts  by Lemma 2.1. Hence
by Lemma 2.1. Hence

Since  for
for  , the inequality in (2.48) holds a.e. on
, the inequality in (2.48) holds a.e. on  , and therefore, the inequality in (2.49) is true for a.e.
, and therefore, the inequality in (2.49) is true for a.e.  . Integrating
. Integrating  over
over  gives
gives

Then

Hence  , which contradicts (2.53) with
, which contradicts (2.53) with  .
.
3. Main Results and an Example
Theorem 3.1.
Suppose there are ( )–(
)–( ), then the following assertions hold.
), then the following assertions hold.
(i)For each  problem (1.1), (1.2) has a sequential solution.
problem (1.1), (1.2) has a sequential solution.
(ii)Any sequential solution of problem (1.1), (1.2) is either a positive solution, a pseudo-dead-core solution, or a dead-core solution.
Proof.
-
(i)
Fix
 . By Lemma 2.6, for each
. By Lemma 2.6, for each 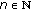 problem (1.12), (1.2) has a solution
problem (1.12), (1.2) has a solution  . Lemmas 2.1 and 2.7 guarantee that
. Lemmas 2.1 and 2.7 guarantee that 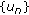 is bounded in
is bounded in  and
and  is equicontinuous on
is equicontinuous on 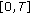 . By the Arzelà-Ascoli theorem, there exist
. By the Arzelà-Ascoli theorem, there exist  and a subsequence
and a subsequence  of
of  such that
such that 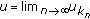 in
in 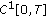 . Hence
. Hence  is a sequential solution of problem (1.1), (1.2).
is a sequential solution of problem (1.1), (1.2). -
(ii)
Let
 be a sequential solution of problem (1.1), (1.2). Then
be a sequential solution of problem (1.1), (1.2). Then  and
and 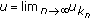 in
in 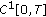 , where
, where 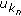 is a solution of problem (1.12), (1.2) with
is a solution of problem (1.12), (1.2) with  replaced by
replaced by 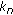 . Hence
. Hence  and
and 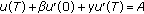 , that is,
, that is,  fulfils the boundary condition (1.2). It follows from the properties of
fulfils the boundary condition (1.2). It follows from the properties of  given in Lemmas 2.1 and 2.3 that
given in Lemmas 2.1 and 2.3 that  for
for  ,
, 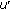 is nondecreasing on
is nondecreasing on 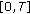 and
and  for
for 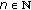 , where
, where 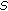 is a positive constant. The next part of the proof is divided into two cases if
is a positive constant. The next part of the proof is divided into two cases if 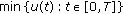 is positive, or is equal to zero.
is positive, or is equal to zero.
Case 1.
Suppose that  . Then there exist
. Then there exist  and
and  ,
,  such that
such that

Hence (cf. (1.8))  for a.e.
for a.e.  and all
and all  . Since
. Since  for some
for some  by Lemma 2.1, we have
by Lemma 2.1, we have  for
for  , and therefore,
, and therefore,

Essentially, the same reasoning shows that

Passing if necessary to a subsequence, we may assume that  is convergent, and let
is convergent, and let  . Letting
. Letting  in (3.2) and (3.3) gives
in (3.2) and (3.3) gives

Hence  is the unique zero of
is the unique zero of  ,
,  since
since  fulfils (1.2), and
fulfils (1.2), and

In addition, it follows from the Fatou lemma and from the relation

that  . Therefore,
. Therefore,  . We now show that
. We now show that  and
and  fulfils (1) a.e. on
fulfils (1) a.e. on  . Let us choose
. Let us choose  . In view of (3.1), (3.4), (3.5) and Lemma 2.1, there exist
. In view of (3.1), (3.4), (3.5) and Lemma 2.1, there exist  and
and  such that
such that

Then (cf. (1.11))

for a.e.  and
and  . Letting
. Letting  in
in

yields

for  by the Lebesgue dominated convergence theorem. Since
by the Lebesgue dominated convergence theorem. Since  satisfying
satisfying  are arbitrary and
are arbitrary and  , equality (3.10) holds for
, equality (3.10) holds for  . Essentially, the same reasoning which is now applied to
. Essentially, the same reasoning which is now applied to  satisfying
satisfying  gives
gives

for  . Hence
. Hence  and
and  fulfills (1.1) a.e. on
fulfills (1.1) a.e. on  . Consequently,
. Consequently,  is a positive solution of problem (1.1), (1.2).
is a positive solution of problem (1.1), (1.2).
Case 2.
Suppose that  , and let
, and let  for some
for some  and
and  on
on  . Since
. Since  is nondecreasing on
is nondecreasing on  , we have
, we have  on
on  ,
,  on
on  and
and  on
on  . Consequently,
. Consequently,  on
on  and
and

Furthermore, it follows from

that  is integrable on the intervals
is integrable on the intervals  and
and  by the Fatou lemma. We can now proceed analogously to Case 1 with
by the Fatou lemma. We can now proceed analogously to Case 1 with  and with
and with  and obtain
and obtain

It follows from these equalities and from  on
on  that
that  and that
and that  fulfils (1.1) a.e. on
fulfils (1.1) a.e. on  . Hence
. Hence  is a dead-core solution of problem (1.1), (1.2) if
is a dead-core solution of problem (1.1), (1.2) if  , and
, and  is a pseudo-dead-core solution if
is a pseudo-dead-core solution if  .
.
Theorem 3.2.
Let ( )–(
)–( ) hold. Then there exists
) hold. Then there exists  such that for each
such that for each  , all sequential solutions of problem (1.1), (1.2) are positive solutions.
, all sequential solutions of problem (1.1), (1.2) are positive solutions.
Proof.
Let  and
and  be given in Lemma 2.8. Let us choose an arbitrary
be given in Lemma 2.8. Let us choose an arbitrary  . Then (2.38) holds, where
. Then (2.38) holds, where  is any solution of problem (1.12), (1.2). Let
is any solution of problem (1.12), (1.2). Let  be a sequential solution of problem (1.1), (1.2). Then
be a sequential solution of problem (1.1), (1.2). Then  in
in  , where
, where  is a solution of (1.12), (1.2) with
is a solution of (1.12), (1.2) with  replaced by
replaced by  . Consequently,
. Consequently,  on
on  by (2.38), which means that
by (2.38), which means that  is a positive solution of problem (1.1), (1.2) by Theorem 3.1.
is a positive solution of problem (1.1), (1.2) by Theorem 3.1.
Theorem 3.3.
Let ( )–(
)–( ) hold. Then for each
) hold. Then for each  , there exists
, there exists  such that any sequential solution
such that any sequential solution  of problem (1.1), (1.2) with
of problem (1.1), (1.2) with  satisfies the equality
satisfies the equality

which means that the dead-core of  contains the interval
contains the interval  . Consequently, all sequential solutions of problem (1.1), (1.2) are dead-core solutions for sufficiently large value of
. Consequently, all sequential solutions of problem (1.1), (1.2) are dead-core solutions for sufficiently large value of  .
.
Proof.
Fix  . Then, by Lemma 2.9, there exists
. Then, by Lemma 2.9, there exists  such that
such that

where  is any solution of problem (1.12), (1.2) with
is any solution of problem (1.12), (1.2) with  . Let us choose
. Let us choose  and let
and let  be a sequential solution of problem (1.1), (1.2). Then
be a sequential solution of problem (1.1), (1.2). Then  in
in  , where
, where  is a solution of problem (1.12), (1.2) with
is a solution of problem (1.12), (1.2) with  replaced by
replaced by  . It follows from (3.16) that
. It follows from (3.16) that  for
for  , and since
, and since  is nondecreasing on
is nondecreasing on  , (3.15) holds. Consequently,
, (3.15) holds. Consequently,  is a dead-core solution of problem (1.1), (1.2) by Theorem 3.1.
is a dead-core solution of problem (1.1), (1.2) by Theorem 3.1.
Example 3.4.
Let  ,
,  ,
,  ,
,  and
and  be positive. Consider the differential equation
be positive. Consider the differential equation

Equation (3.17) is the special case of (1.1) with  and
and  . Since
. Since

for 
 , where
, where  ,
,  fulfils
fulfils  with
with  ,
,  ,
,  ,
,  and
and  . Hence, by Theorem 3.1, problem (3.17), (1.2) has a sequential solution for each
. Hence, by Theorem 3.1, problem (3.17), (1.2) has a sequential solution for each  , and any sequential solution is either a positive solution or a pseudo-dead-core solution or a dead-core solution. If the values of
, and any sequential solution is either a positive solution or a pseudo-dead-core solution or a dead-core solution. If the values of  are sufficiently small, then all sequential solutions of problem (3.17), (1.2) are positive solutions by Theorem 3.2. Theorem 3.3 guarantees that all sequential solutions of problem (3.17), (1.2) are dead-core solutions for sufficiently large values of
are sufficiently small, then all sequential solutions of problem (3.17), (1.2) are positive solutions by Theorem 3.2. Theorem 3.3 guarantees that all sequential solutions of problem (3.17), (1.2) are dead-core solutions for sufficiently large values of  .
.
References
Agarwal RP, O'Regan D, Staněk S: Positive and dead core solutions of singular Dirichlet boundary value problems with -Laplacian. Computers & Mathematics with Applications 2007,54(2):255–266. 10.1016/j.camwa.2006.12.026
Agarwal RP, O'Regan D, Staněk S: Dead cores of singular Dirichlet boundary value problems with -Laplacian. Applications of Mathematics 2008,53(4):381–399. 10.1007/s10492-008-0031-z
Agarwal RP, O'Regan D, Staněk S: Dead core problems for singular equations with -Laplacian. Boundary Value Problems 2007, 2007:-16.
Baxley JV, Gersdorff GS: Singular reaction-diffusion boundary value problems. Journal of Differential Equations 1995,115(2):441–457. 10.1006/jdeq.1995.1022
Bobisud LE: Asymptotic dead cores for reaction-diffusion equations. Journal of Mathematical Analysis and Applications 1990,147(1):249–262. 10.1016/0022-247X(90)90396-W
Pulverer G, Staněk S, Weinmüller EB: Analysis and numerical solutions of positive and dead core solutions of singular Sturm-Liouville problems. submitted
Staněk S, Pulverer G, Weinmüller EB: Analysis and numerical simulation of positive and dead-core solutions of singular two-point boundary value problems. Computers & Mathematics with Applications 2008,56(7):1820–1837. 10.1016/j.camwa.2008.03.029
Aris R: The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts. Clarendon Press, Oxford, UK; 1975.
Bobisud LE, O'Regan D, Royalty WD: Existence and nonexistence for a singular boundary value problem. Applicable Analysis 1988,28(4):245–256. 10.1080/00036818808839765
Staněk S: Positive and dead core solutions of singular BVPs for third-order differential equations. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):e153-e163. 10.1016/j.na.2008.10.013
Agarwal RP, O'Regan D, Staněk S: General existence principles for nonlocal boundary value problems with -Laplacian and their applications. Abstract and Applied Analysis 2006, 2006:-30.
Rachůnková I, Staněk S, Tvrdý M: Singularities and Laplacians in boundary value problems for nonlinear ordinary differential equations. In Handbook of Differential Equations: Ordinary Differential Equations. Vol. III, Handbook of Differential Equations. Edited by: Cañada A, Drábek P, Fonda A. Elsevier/North-Holland, Amsterdam, The Netherlands; 2006:607–722.
Rachůnková I, Staněk S, Tvrdý M: Solvability of Nonlinear Singular Problems for Ordinary Differential Equations, Contemporary Mathematics and Its Applications. Volume 5. Hindawi Publishing Corporation, New York, NY, USA; 2008:x+268.
Acknowledgment
This work was supported by the Council of Czech Government MSM 6198959214.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Staněk, S. Positive and Dead-Core Solutions of Two-Point Singular Boundary Value Problems with ϕ-Laplacian. Adv Differ Equ 2010, 262854 (2010). https://doi.org/10.1155/2010/262854
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/262854
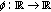 is an increasing and odd homeomorphism such that
is an increasing and odd homeomorphism such that  .
. , where
, where  , and
, and
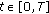 and all
and all  ,
,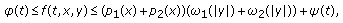
 . By Lemma 2.6, for each
. By Lemma 2.6, for each 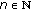 problem (1.12), (1.2) has a solution
problem (1.12), (1.2) has a solution  . Lemmas 2.1 and 2.7 guarantee that
. Lemmas 2.1 and 2.7 guarantee that 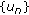 is bounded in
is bounded in  and
and  is equicontinuous on
is equicontinuous on 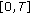 . By the Arzelà-Ascoli theorem, there exist
. By the Arzelà-Ascoli theorem, there exist  and a subsequence
and a subsequence  of
of  such that
such that 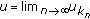 in
in 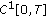 . Hence
. Hence  is a sequential solution of problem (1.1), (1.2).
is a sequential solution of problem (1.1), (1.2). be a sequential solution of problem (1.1), (1.2). Then
be a sequential solution of problem (1.1), (1.2). Then  and
and 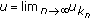 in
in 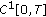 , where
, where 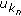 is a solution of problem (1.12), (1.2) with
is a solution of problem (1.12), (1.2) with  replaced by
replaced by 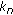 . Hence
. Hence  and
and 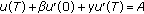 , that is,
, that is,  fulfils the boundary condition (1.2). It follows from the properties of
fulfils the boundary condition (1.2). It follows from the properties of  given in Lemmas 2.1 and 2.3 that
given in Lemmas 2.1 and 2.3 that  for
for  ,
, 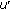 is nondecreasing on
is nondecreasing on 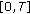 and
and  for
for 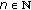 , where
, where 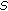 is a positive constant. The next part of the proof is divided into two cases if
is a positive constant. The next part of the proof is divided into two cases if 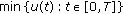 is positive, or is equal to zero.
is positive, or is equal to zero.