- Research Article
- Open access
- Published:
Stabilization with Optimal Performance for Dissipative Discrete-Time Impulsive Hybrid Systems
Advances in Difference Equations volume 2010, Article number: 278240 (2010)
Abstract
This paper studies the problem of stabilization with optimal performance for dissipative DIHS (discrete-time impulsive hybrid systems). By using Lyapunov function method, conditions are derived under which the DIHS with zero inputs is GUAS (globally uniformly asymptotically stable). These GUAS results are used to design feedback control law such that a dissipative DIHS is asymptotically stabilized and the value of a hybrid performance functional can be minimized. For the case of linear DIHS with a quadratic supply rate and a quadratic storage function, sufficient and necessary conditions of dissipativity are expressed in matrix inequalities. And the corresponding conditions of optimal quadratic hybrid performance are established. Finally, one example is given to illustrate the results.
1. Introduction
In many engineering problems, it is needed to consider the energy of systems. The energy of a controlled system is often linked to the concept of dissipativity [1–4]. A dissipative system here is one for which the energy dissipated inside the dynamical system is less than the energy supplied from the external source. The "energy" storage function of a dissipative system which can be viewed as generalization of energy function is often used to be a Lyapunov function, and thus the stability of a dissipative system can be investigated. It is also known that a dissipative system may be unstable. If one hopes that a dissipative but unstable system will be stable, it is necessary to use the technique of stabilization.
Feedback stabilization and dissipativity theory as well as the connected Lyapunov stability theory has been studied for systems possessing continuous motions. Byrnes et al. started to study the dissipativity and stabilization of continuous systems based on geometric system theory in [5, 6] and relevant references cited therein. Recently, notions of classical dissipativity theory have been extended for CIHS (continuous-time impulsive hybrid systems; see [7–16]), switched systems, discrete-time systems, and discontinuous systems, see [17–24]. But these reports include very few results of feedback stabilization for dissipative CIHS. The traditional methods used in the study of feedback stabilization of dissipative continuous-time systems are those based on the LaSalle invariance principle [25]. But it is difficult to use it to analyze the feedback stabilization of dissipative CIHS because solutions of impulsive hybrid systems are no longer continuous. In [14], feedback stabilization of dissipative CIHS is studied by using Lyapunov-like function, which is derived from the "energy" storage function of a dissipative CIHS. However, to the best of our knowledge, no dissipativity and feedback stabilization results have been previously reported for DIHS (discrete-time impulsive hybrid systems, see [26–28]), in which the impulses occur in discrete-time systems. Recently, in [29, 30] and the relevant references cited therein, the optimal control issue is also reported for CIHS and the Pontryagin-type Maximum Principle for CIHS is established. However, there are fewer results reported for stabilization with optimal performance for dissipative CIHS or DIHS.
The objective of this paper is to study the stabilization with optimal performance problem for dissipative DIHS in the spirit of [14, 20]. By using the Lyapunov function and dwell time method, we propose some GUAS results for DIHS. Then these GUAS results are used to derive the conditions under which a dissipative DIHS is asymptotically stabilized and the hybrid performance functional is minimized.
The rest of this paper is organized as follows. In Section 2, we introduce some notations and definitions. In Section 3, we give the main results for DIHS. Then, we specialize the results to linear DIHS. Finally, in Section 4, we discuss one example to illustrate our results.
2. Preliminaries
Let  denote the
denote the  -dimensional Euclidean space. Let
-dimensional Euclidean space. Let  and
and  . A function
. A function  is of class-
is of class- (
( ) if it is continuous, zero at zero and strictly increasing. It is of class-
) if it is continuous, zero at zero and strictly increasing. It is of class- if it is of class-
if it is of class- and is unbounded. For
and is unbounded. For  satisfying
satisfying  , denote
, denote  ,
,  , and
, and  .
.  (
( ),
),  , means that matrix
, means that matrix  is a positive definite (nonnegative definite) and symmetric matrix. Let
is a positive definite (nonnegative definite) and symmetric matrix. Let  stand for the Euclidean norm in
stand for the Euclidean norm in  .
.
Consider the following controlled DIHS:

where  is the state;
is the state;  are the outputs;
are the outputs;  are known continuous functions with
are known continuous functions with  ;
;  and satisfies
and satisfies  ;
;  and satisfies
and satisfies  ;
;  are external control inputs with
are external control inputs with  , here
, here  is the class of admissible hybrid control inputs;
is the class of admissible hybrid control inputs;  ; and the impulsive sequence
; and the impulsive sequence  satisfie:
satisfie:  and
and  , with
, with  and
and  . Let
. Let  be the solution of system (2.1) with initial condition
be the solution of system (2.1) with initial condition  . For the impulsive sequence
. For the impulsive sequence  and any
and any  satisfying
satisfying  , we denote
, we denote  the number of impulses during
the number of impulses during  .
.
The hybrid performance functional of DIHS (2.1) is

where  with
with  ,
,  or
or  , and
, and  are given and known functions.
are given and known functions.
Remark 2.1.
-
(i)
If there exists a positive integer
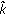 such that
such that  , then (2.1) becomes a normal discrete-time system with initial point
, then (2.1) becomes a normal discrete-time system with initial point 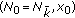 . In this paper, we study the DIHS under the following assumption:
. In this paper, we study the DIHS under the following assumption: 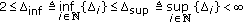 (23)
(23)
-
(ii)
By (2.3), we get the fact that for any
 ,
, 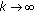 if and only if
if and only if  .
.
Definition 2.2.
A function  , where
, where  ,
,  with
with  and
and  , is called a supply rate of (2.1) if
, is called a supply rate of (2.1) if  and
and  are locally summable: for all input-output pairs
are locally summable: for all input-output pairs  and any
and any  with
with  ,
,  satisfy
satisfy 
Definition 2.3.
DIHS (2.1) is said to be dissipative under supply rate  if there exists a nonnegative continuous function
if there exists a nonnegative continuous function  with
with  , called storage function, such that for all
, called storage function, such that for all  the following dissipation inequality holds for any
the following dissipation inequality holds for any  with
with  ,
,

Lemma 2.4.
DIHS (2.1) is dissipative under the supply rate  if and only if there exists a nonnegative continuous function
if and only if there exists a nonnegative continuous function  with
with  such that
such that

where  .
.
Proof.
By using Definition 2.3, it is easy to get that (2.4) is equivalent to (2.5). The details are omitted here.
2.1. Stabilization with Optimal Performance Problem
For the dissipative DIHS (2.1) with hybrid performance functional (2.2), the stabilization with optimal performance problem is to design the state feedback control law  , where
, where  with
with  , such that the closed-loop system
, such that the closed-loop system

is GUAS. Moreover,  can minimize
can minimize  .
.
3. Main Results
In this section, by using the Lyapunov function method, some GUAS criteria are established for DIHS. Then, these stability criteria are used to study the optimal stabilization issue for a dissipative DIHS with hybrid performance functional.
Theorem 3.1.
Let  . Suppose (2.3) holds and furthermore assume that there exists a function
. Suppose (2.3) holds and furthermore assume that there exists a function  such that
such that
-
(i)
there exist
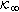 -functions
-functions 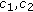 such that for any
such that for any  ,
,  (31)
(31)
-
(ii)
there exists a
 satisfying
satisfying 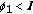 and
and  (32)
(32)
where  is the identity function:
is the identity function:  for any
for any  ;
;
-
(iii)
for
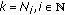 , there exists
, there exists  -function
-function  such that
such that 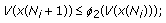 (33)
(33)
-
(iv)
there exists a sufficient large
 , such that
, such that 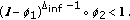 (34)
(34)
Then, DIHS (2.1) with  is GUAS.
is GUAS.
Proof.
Denote  . By condition (ii), we get that, for any
. By condition (ii), we get that, for any  ,
,

It follows from (3.5) and condition (iii) that

For any  , there exists an
, there exists an  such that
such that  . By (3.6) and conditions (i)–(iii), we have
. By (3.6) and conditions (i)–(iii), we have

Hence, for any  , let
, let  ; then, when
; then, when  , we get from (3.7) that
, we get from (3.7) that  for any
for any  . Thus, the system (2.1) is GUS (globally uniformly stable).
. Thus, the system (2.1) is GUS (globally uniformly stable).
Denote  . It follows from (3.6) that
. It follows from (3.6) that

Since by condition (iv),  for any
for any  , thus we get that the sequence
, thus we get that the sequence  is monotone decreasing and
is monotone decreasing and  exists. If
exists. If  , then,
, then,  . This contradiction implies
. This contradiction implies  , that is,
, that is, 
For any  , by conditions (i)–(iii), we have
, by conditions (i)–(iii), we have  It follows from Remark 2.1(ii) that
It follows from Remark 2.1(ii) that  . Hence, DIHS (2.1) with
. Hence, DIHS (2.1) with  is uniformly attractive and hence it is GUAS. The proof is complete.
is uniformly attractive and hence it is GUAS. The proof is complete.
Theorem 3.2.
Let  and suppose (2.3) holds and furthermore assume that there exists a
and suppose (2.3) holds and furthermore assume that there exists a  satisfying conditions (i) and (iii) of Theorem 3.1 and
satisfying conditions (i) and (iii) of Theorem 3.1 and
(ii*) there exists a  such that
such that

(iv*) there exists a sufficient large  , such that
, such that

Then, DIHS (2.1) with  is GUAS.
is GUAS.
Proof.
By similar proof of Theorem 3.1 with  , we obtain that the result holds. The detailed is omitted here.
, we obtain that the result holds. The detailed is omitted here.
Corollary 3.3.
Let  and suppose (2.3) holds and assume that there exists a function
and suppose (2.3) holds and assume that there exists a function  satisfying (3.1) and
satisfying (3.1) and
-
(i)
there exists a constant
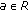 satisfying
satisfying  and
and  (311)
(311)
-
(ii)
for
 , there exists a constant
, there exists a constant  such that
such that  (312)
(312)
-
(iii)
one of the following cases holds.
Case 1.
There exists a sufficient large  , such that
, such that

Case 2.
There exists a sufficient large  , such that
, such that

Then, DIHS (2.1) with  is GUAS.
is GUAS.
Proof.
The result is the direct consequence of Theorems 3.1 and 3.2, where in Case 1, let  , while in Case 2, let
, while in Case 2, let  for any
for any  .
.
Remark 3.4.
Theorems 3.1 and 3.2 and Corollary 3.3 give two kinds of GUAS properties of DIHS by using the method of Lyapunov function and maximal and minimal dwell times . For more detailed stability results of DIHS, please refer to the literature [26–28] and relevant references cited therein.
. For more detailed stability results of DIHS, please refer to the literature [26–28] and relevant references cited therein.
Theorem 3.5.
Suppose (2.3) holds and assume that under the given supply rate  , DIHS (2.1) is dissipative with a storage function
, DIHS (2.1) is dissipative with a storage function  satisfying (3.1), and that there exist functions
satisfying (3.1), and that there exist functions  with
with  , such that
, such that
-
(i)
there exist
 with
with 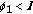 satisfying (3.4) and
satisfying (3.4) and 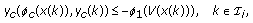 (315)
(315)

-
(ii)
the following equations and inequalities are satisfied:
 (317)
(317)
where  and
and .
.
Then, under  , the closed-loop system (2.6) is GUAS, and
, the closed-loop system (2.6) is GUAS, and

Specially, 
Proof.
Since system (2.1) is dissipative under the supply rate  , then, for
, then, for  , we get
, we get

From condition (i) and (3.19), we derive that

Thus, from (3.20) and Theorem 3.1, we obtain that the closed-loop system (2.6) is GUAS.
By condition (ii), for  , we get
, we get

Denote  . From (3.21), we have
. From (3.21), we have

Thus, from (3.22) condition (i), and the fact that the closed-loop system is GUAS, we obtain that

Now, we prove that  minimizes
minimizes  . From condition (ii), we have
. From condition (ii), we have

Thus, using (3.24), (3.22), and  , we have
, we have

Hence, (3.18) holds and all the results hold.
Theorem 3.6.
Suppose (2.3) holds and assume that under the supply rate  , system (2.1) is dissipative with a storage function
, system (2.1) is dissipative with a storage function  satisfying (3.1), and that there exist functions
satisfying (3.1), and that there exist functions  with
with  , such that (ii) of Theorem 3.5 holds while (i) of Theorem 3.5 is replaced by the following:
, such that (ii) of Theorem 3.5 holds while (i) of Theorem 3.5 is replaced by the following:
(i*) there exist  with
with  satisfying (3.10) and
satisfying (3.10) and


Then, all results of Theorem 3.5 still hold.
Proof.
By similar proof of Theorem 3.5 and using the result of Theorem 3.2, we obtain that all results are true.
Remark 3.7.
-
(i)
For a dissipative DIHS (2.1) with supply rate
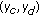 and "energy" storage function
and "energy" storage function 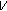 , if
, if  or
or  is negative during some time interval or at some time instance, then it implies that the "energy" of system will be decreasing during this period or at this instance. These two kinds of dissipativity properties all help to achieve the stability for whole DIHS. In Theorem 3.5, the negative supply rate
is negative during some time interval or at some time instance, then it implies that the "energy" of system will be decreasing during this period or at this instance. These two kinds of dissipativity properties all help to achieve the stability for whole DIHS. In Theorem 3.5, the negative supply rate 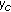 leads to the decreasing of "energy" of system during two consecutive impulses (see (3.15)) and thus it permits to some extend the increasing of "energy" at impulsive instances (see (3.16)) while the stability property of whole system will be kept. On the other hand, in Theorem 3.6, the negative supply rate
leads to the decreasing of "energy" of system during two consecutive impulses (see (3.15)) and thus it permits to some extend the increasing of "energy" at impulsive instances (see (3.16)) while the stability property of whole system will be kept. On the other hand, in Theorem 3.6, the negative supply rate  leads to the decreasing of "energy" of system at impulse instances (see (3.27)) and thus it permits to some extend of increasing of "energy" during two consecutive impulses (see (3.26)) while the stability property of whole system can still be guaranteed.
leads to the decreasing of "energy" of system at impulse instances (see (3.27)) and thus it permits to some extend of increasing of "energy" during two consecutive impulses (see (3.26)) while the stability property of whole system can still be guaranteed.
In the literature, if the stability property is derived from the dissipativity of system, it often needs the condition of negative supply rate. But one can see from Theorems 3.5 and 3.6 that this condition is relaxed for DIHS.
-
(ii)
By (3.17), if
 and
and 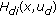 are continuously differential in
are continuously differential in  , respectively, then, for
, respectively, then, for 
 (328)
(328)
which can be used to derive the hybrid state feedback control law  .
.
At the end of section, we specialize the results obtained to the case of linear DIHS with a quadratic supply rate.
Consider the following linear DIHS:

with the hybrid quadratic performance functional:

where  are matrices with appropriate dimensions and
are matrices with appropriate dimensions and  and
and  .
.
The quadratic supply rate  is given by
is given by

where  are matrices with appropriate dimensions and
are matrices with appropriate dimensions and  are symmetric matrices.
are symmetric matrices.
Denote  and
and  .
.
Theorem 3.8.
Assume that  ,
,  and for
and for  , the linear DIHS (3.29) is dissipative with storage function
, the linear DIHS (3.29) is dissipative with storage function  , where
, where  , if and only if the following LMIs are satisfied:
, if and only if the following LMIs are satisfied:

Moreover, if  satisfy
satisfy


where  satisfy
satisfy  and the condition (iii) of Corollary 3.3, then, the state feedback control law
and the condition (iii) of Corollary 3.3, then, the state feedback control law

can stabilize system (3.29), and minimizes  , that is,
, that is,

Proof.
By (3.29), it is not difficult to get that

where for  ,
,  , and
, and  ,
,  ,
,  .
.
Thus, by Lemma 2.4, we get that system (3.29) is dissipative if and only if  . By Schur Complement Theorem [31], for
. By Schur Complement Theorem [31], for  , it is not hard to get that
, it is not hard to get that  if and only if LMI
if and only if LMI  holds. Hence, we obtain that system (3.29) is dissipative if and only if LMIs (3.32)
holds. Hence, we obtain that system (3.29) is dissipative if and only if LMIs (3.32)  hold.
hold.
Let  , where
, where  ; then, it follows from (3.33) that for
; then, it follows from (3.33) that for  ,
,

Thus, by Corollary 3.3, the closed-loop system given by (3.29) and (3.35) is GUAS.
Now, we show that (3.35) also minimizes  .
.
Denote:  and
and  Then, by (3.34), we obtain
Then, by (3.34), we obtain

Hence, by  , we get
, we get

Clearly, if  , then, by (3.39), we have
, then, by (3.39), we have

Then, by Theorem 3.5, the result of this theorem follows readily. The proof is complete.
Corollary 3.9.
Assume that  ,
,  and there exists a matrix
and there exists a matrix  satisfying LMI (3.32), (3.34), and the following matrix inequalities:
satisfying LMI (3.32), (3.34), and the following matrix inequalities:

where  ,
,  ,
,  , and
, and  if
if  ,
,  if
if  ; and
; and  for
for  ; and where constants
; and where constants  satisfy the condition (iii) of Corollary 3.3.
satisfy the condition (iii) of Corollary 3.3.
Then, all the results of Theorem 3.8 still hold.
Proof.
By Schur Complement Theorem [31] and Theorem 3.8, the result of this corollary follows.
4. Examples
In this section, one example is solved to illustrate the obtained results.
Example 4.1.
Consider DIHS in form of (3.29) where

The matrices appeared in (3.31) and (3.30) are given by 
 and
and

By solving (3.32), we obtain

Thus, by Theorem 3.8, this system is dissipative under the quadratic supply rate. Moreover, we see that  and
and  . And by solving (3.42), we get
. And by solving (3.42), we get  and
and

Thus, by (3.14) of Corollary 3.3, if  satisfies
satisfies  , that is,
, that is,  , then, all the conditions of Corollary 3.9 are satisfied. Therefore,
, then, all the conditions of Corollary 3.9 are satisfied. Therefore,  given by (4.4) can stabilize the closed-loop system and minimizes
given by (4.4) can stabilize the closed-loop system and minimizes  , that is, if
, that is, if  , then
, then

5. Conclusions
In this paper, by establishing the GUAS results for DIHS, we have obtained the conditions under which a dissipative DIHS with a hybrid performance functional can be asymptotically stabilized by a feedback control law and meantime the hybrid performance functional is optimized. For the case of linear DIHS with a quadratic supply rate and a quadratic hybrid performance functional, the corresponding sufficient conditions are changed into matrix inequalities. One example verifies the theoretic results obtained.
References
Willems JC: Dissipative dynamical systems—part I: general theory. Archive for Rational Mechanics and Analysis 1972, 45: 321-351. 10.1007/BF00276493
Willems JC: Dissipative dynamical systems—part II: linear systems with quadratic supply rates. Archive for Rational Mechanics and Analysis 1972,45(5):352-393. 10.1007/BF00276494
Hill D, Moylan P: The stability of nonlinear dissipative systems. IEEE Transactions on Automatic Control 1976,21(5):708-711. 10.1109/TAC.1976.1101352
Hill DJ, Moylan PJ: Dissipative dynamical systems: basic input-output and state properties. Journal of the Franklin Institute 1980,309(5):327-357. 10.1016/0016-0032(80)90026-5
Byrnes CI, Isidori A: New results and examples in nonlinear feedback stabilization. Systems & Control Letters 1989,12(5):437-442. 10.1016/0167-6911(89)90080-7
Byrnes CI, Isidori A, Willems JC: Passivity, feedback equivalence, and the global stabilization of minimum phase nonlinear systems. IEEE Transactions on Automatic Control 1991,36(11):1228-1240. 10.1109/9.100932
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Yang T: Impulsive Control Theory, Lecture Notes in Control and Information Sciences. Volume 272. Springer, Berlin, Germany; 2001:xx+348.
Li Z, Soh Y, Wen C: Switched and Impulsive Systems: Analysis, Design and Application, Lecture Notes in Control and Information Sciences. Volume 313. Springer, Berlin, Germany; 2005:xviii+271.
Zhang Y, Sun J: Stability of impulsive linear differential equations with time delay. IEEE Transactions on Circuits and Systems II 2005,52(10):701-705. 10.1109/TCSII.2005.852187
Guan Z, Hill DJ, Shen X: On hybrid impulsive and switching systems and application to nonlinear control. IEEE Transactions on Automatic Control 2005,50(7):1058-1062. 10.1109/TAC.2005.851462
Basin MV, Pinsky MA: On impulse and continuous observation control design in Kalman filtering problem. Systems & Control Letters 1999,36(3):213-219. 10.1016/S0167-6911(98)00094-2
Chen W-H, Zheng WX: Global exponential stability of impulsive neural networks with variable delay: an LMI approach. IEEE Transactions on Circuits and Systems I 2009,56(6):1248-1259. 10.1109/TCSI.2008.2006210
Liu B, Liu X, Teo KL: Feedback stabilization of dissipative impulsive dynamical systems. Information Sciences 2007,177(7):1663-1672. 10.1016/j.ins.2006.09.019
Chen W-H, Wang J-G, Tang Y-J, Lu X:Robust
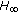 control of uncertain linear impulsive stochastic systems. International Journal of Robust and Nonlinear Control 2008,18(13):1348-1371. 10.1002/rnc.1286
control of uncertain linear impulsive stochastic systems. International Journal of Robust and Nonlinear Control 2008,18(13):1348-1371. 10.1002/rnc.1286Chen W-H, Zheng WX:Robust stability and
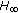 -control of uncertain impulsive systems with time-delay. Automatica 2009,45(1):109-117. 10.1016/j.automatica.2008.05.020
-control of uncertain impulsive systems with time-delay. Automatica 2009,45(1):109-117. 10.1016/j.automatica.2008.05.020Zhao J, Hill DJ: Dissipativity theory for switched systems. IEEE Transactions on Automatic Control 2008,53(4):941-953. 10.1109/TAC.2008.920237
Haddad WM, Chellaboina V, Kablar NA: Nonlinear impulsive dynamical systems—part I: stability and dissipativity. Proceedings of the 38th IEEE Conference on Decision and Control (CDC '99), December 1999, Phoenix, Ariz, USA 5: 4404-4422.
Haddad WM, Chellaboina V, Kablar NA: Nonlinear impulsive dynamical systems—part II: feedback interconnections and optimality. Proceeedings of the 38th IEEE Conference on Decision and Control (CDC '99), December 1999, Phoenix, Ariz, USA 5: 5225-5234.
Haddad WM, Hui Q, Chellaboina V, Nersesov S: Vector dissipativity theory for discrete-time large-scale nonlinear dynamical systems. Advances in Difference Equations 2004,2004(1):37-66. 10.1155/S1687183904310071
Haddad WM, Chellaboina V, Nersesov SG: Impulsive and Hybrid Dynamical Systems: Stability, Dissipativity, and Control, Princeton Series in Applied Mathematics. Princeton University Press, Princeton, NJ, USA; 2006:xvi+504.
Haddad WM, Hui Q: Dissipativity theory for discontinuous dynamical systems: basic input, state, and output properties, and finite-time stability of feedback interconnections. Nonlinear Analysis: Hybrid Systems 2009,3(4):551-564. 10.1016/j.nahs.2009.04.006
Liu B, Liu X, Liao X: Robust dissipativity for uncertain impulsive dynamical systems. Mathematical Problems in Engineering 2003,2003(3-4):119-128. 10.1155/S1024123X03204014
Lei M, Liu B: Robust impulsive synchronization of discrete dynamical networks. Advances in Difference Equations 2008, 2008:-17.
LaSalle LP, Lefschetz S: Stability by Lyapunov's Direct Method. Academic Press, New York, NY, USA; 1961.
Liu B, Hill DJ: Comparison principle and stability of discrete-time impulsive hybrid systems. IEEE Transactions on Circuits and Systems I 2009,56(1):233-245. 10.1109/TCSI.2008.924897
Liu B, Liu X: Robust stability of uncertain discrete impulsive systems. IEEE Transactions on Circuits and Systems II 2007,54(5):455-459. 10.1109/TCSII.2007.892395
Liu B, Liu X: Uniform stability of discrete impulsive systems. International Journal of Systems Science 2008,39(2):181-192. 10.1080/00207720701748380
Azhmyakov V, Boltyanski VG, Poznyak A: Optimal control of impulsive hybrid systems. Nonlinear Analysis: Hybrid Systems 2008,2(4):1089-1097. 10.1016/j.nahs.2008.09.003
Cardoso RTN, Takahashi RHC: Solving impulsive control problems by discrete-time dynamic optimization methods. Tendências em Matemática Aplicada e Computacional 2008,9(1):21-30.
Boyd SP, El Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia, Pa, USA; 1994.
Acknowledgments
The authors would like to thank the Editor, Professor Jianshe S. Yu, and the anonymous referees for their helpful comments and suggestions. This work was supported by NSFC-China (no. 60874025) and ARC-Australia (no. DP0881391).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yan, L., Liu, B. Stabilization with Optimal Performance for Dissipative Discrete-Time Impulsive Hybrid Systems. Adv Differ Equ 2010, 278240 (2010). https://doi.org/10.1155/2010/278240
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/278240
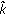 such that
such that  , then (2.1) becomes a normal discrete-time system with initial point
, then (2.1) becomes a normal discrete-time system with initial point 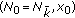 . In this paper, we study the DIHS under the following assumption:
. In this paper, we study the DIHS under the following assumption: 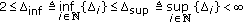
 ,
, 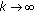 if and only if
if and only if  .
.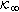 -functions
-functions 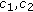 such that for any
such that for any  ,
, 
 satisfying
satisfying 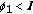 and
and 
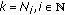 , there exists
, there exists  -function
-function  such that
such that 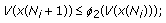
 , such that
, such that 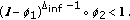
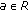 satisfying
satisfying  and
and 
 , there exists a constant
, there exists a constant  such that
such that 
 with
with 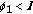 satisfying (3.4) and
satisfying (3.4) and 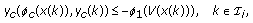

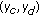 and "energy" storage function
and "energy" storage function 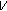 , if
, if  or
or  is negative during some time interval or at some time instance, then it implies that the "energy" of system will be decreasing during this period or at this instance. These two kinds of dissipativity properties all help to achieve the stability for whole DIHS. In Theorem 3.5, the negative supply rate
is negative during some time interval or at some time instance, then it implies that the "energy" of system will be decreasing during this period or at this instance. These two kinds of dissipativity properties all help to achieve the stability for whole DIHS. In Theorem 3.5, the negative supply rate 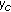 leads to the decreasing of "energy" of system during two consecutive impulses (see (3.15)) and thus it permits to some extend the increasing of "energy" at impulsive instances (see (3.16)) while the stability property of whole system will be kept. On the other hand, in Theorem 3.6, the negative supply rate
leads to the decreasing of "energy" of system during two consecutive impulses (see (3.15)) and thus it permits to some extend the increasing of "energy" at impulsive instances (see (3.16)) while the stability property of whole system will be kept. On the other hand, in Theorem 3.6, the negative supply rate  leads to the decreasing of "energy" of system at impulse instances (see (3.27)) and thus it permits to some extend of increasing of "energy" during two consecutive impulses (see (3.26)) while the stability property of whole system can still be guaranteed.
leads to the decreasing of "energy" of system at impulse instances (see (3.27)) and thus it permits to some extend of increasing of "energy" during two consecutive impulses (see (3.26)) while the stability property of whole system can still be guaranteed. and
and 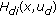 are continuously differential in
are continuously differential in  , respectively, then, for
, respectively, then, for 

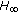 control of uncertain linear impulsive stochastic systems. International Journal of Robust and Nonlinear Control 2008,18(13):1348-1371. 10.1002/rnc.1286
control of uncertain linear impulsive stochastic systems. International Journal of Robust and Nonlinear Control 2008,18(13):1348-1371. 10.1002/rnc.1286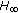 -control of uncertain impulsive systems with time-delay. Automatica 2009,45(1):109-117. 10.1016/j.automatica.2008.05.020
-control of uncertain impulsive systems with time-delay. Automatica 2009,45(1):109-117. 10.1016/j.automatica.2008.05.020