- Research Article
- Open access
- Published:
Boundary Controllability of Nonlinear Fractional Integrodifferential Systems
Advances in Difference Equations volume 2010, Article number: 279493 (2010)
Abstract
Sufficient conditions for boundary controllability of nonlinear fractional integrodifferential systems in Banach space are established. The results are obtained by using fixed point theorems. We also give an application for integropartial differential equations of fractional order.
1. Introduction
Let  and
and  be a pair of real Banach spaces with norms
be a pair of real Banach spaces with norms  and
and  , respectively. Let
, respectively. Let  be a linear closed and densely defined operator with
be a linear closed and densely defined operator with  and let
and let  be a linear operator with
be a linear operator with  and
and  , a Banach space. In this paper we study the boundary controllability of nonlinear fractional integrodifferential systems in the form
, a Banach space. In this paper we study the boundary controllability of nonlinear fractional integrodifferential systems in the form

where  and
and  is a linear continuous operator, and the control function
is a linear continuous operator, and the control function  is given in
is given in  a Banach space of admissible control functions. The nonlinear operators
a Banach space of admissible control functions. The nonlinear operators  and
and  are given and
are given and 
Let  be the linear operator defined by
be the linear operator defined by

The controllability of integrodifferential systems has been studied by many authors (see [1–6]). This work may be regarded as a direct attempt to generalize the work in [7, 8].
2. Main Result
Definition 2.1.
System (1.1) is said to be controllable on the interval  if for every
if for every  there exists a control
there exists a control  such that
such that  of (1.1) satisfies
of (1.1) satisfies 
To establish the result, we need the following hypotheses.
-
(H1)
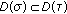 and the restriction of
and the restriction of  to
to 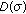 is continuous relative to the graph norm of
is continuous relative to the graph norm of 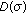 .
. -
(H2) The operator
 is the infinitesimal generator of a compact semigroup
is the infinitesimal generator of a compact semigroup  and there exists a constant
and there exists a constant 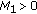 such that
such that 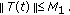
-
(H3) There exists a linear continuous operator
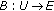 such that
such that 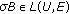 ,
,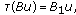 for all
for all  Also
Also  is continuously differentiable and
is continuously differentiable and 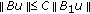 for all
for all  where C is a constant.
where C is a constant. -
(H4) For all
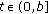 and
and 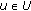 ,
, 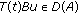 . Moreover, there exists a positive constant
. Moreover, there exists a positive constant  such that
such that 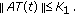
-
(H5) The nonlinear operators
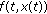 and
and 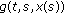 , for
, for 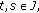 satisfy
satisfy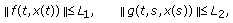 (2.1)
(2.1)where
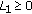 and
and 
-
(H6) The linear operator
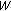 from
from 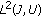 into
into 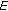 defined by
defined by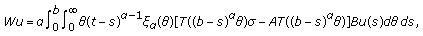 (2.2)
(2.2)
where  is a probability density function defined on
is a probability density function defined on  (see [9, 10]) and induces an invertible operator
(see [9, 10]) and induces an invertible operator  defined on
defined on  and there exists a positive constant
and there exists a positive constant  and
and  such that
such that  and
and  . Let
. Let  be the solution of (1.1). Then we define a function
be the solution of (1.1). Then we define a function  and from our assumption we see that
and from our assumption we see that  . Hence (1.1) can be written in terms of
. Hence (1.1) can be written in terms of  and
and  as
as

If  is continuously differentiable on
is continuously differentiable on  , then
, then  can be defined as a mild solution to be the Cauchy problem
can be defined as a mild solution to be the Cauchy problem

and the solution of (1.1) is given by

Since the differentiability of the control  represents an unrealistic and severe requirement, it is necessary of the solution for the general inputs
represents an unrealistic and severe requirement, it is necessary of the solution for the general inputs  Integrating (2.5) by parts, we get
Integrating (2.5) by parts, we get

Thus (2.6) is well defined and it is called a mild solution of system (1.1).
Theorem 2.2.
If hypotheses (H1)–(H6) are satisfied, then the boundary control fractional integrodifferential system (1.1) is controllable on  .
.
Proof.
Using assumption (H6), for an arbitrary function  define the control
define the control

We shall now show that, when using this control, the operator defined by

has a fixed point. This fixed point is then a solution of (1.1). Clearly,  which means that the control
which means that the control  steers the nonlinear fractional integrodifferential system from the initial state
steers the nonlinear fractional integrodifferential system from the initial state  to
to  in time
in time  , provided we can obtain a fixed point of the nonlinear operator
, provided we can obtain a fixed point of the nonlinear operator  .
.
Let  and
and  where the positive constant
where the positive constant  is given by
is given by

Then  is clearly a bounded, closed, and convex subset of
is clearly a bounded, closed, and convex subset of  . We define a mapping
. We define a mapping  by
by

Consider

Since  and
and  are continuous and
are continuous and  it follows that
it follows that  is also continuous and maps
is also continuous and maps  into itself. Moreover,
into itself. Moreover,  maps
maps  into precompact subset of
into precompact subset of  . To prove this, we first show that, for every fixed
. To prove this, we first show that, for every fixed  , the set
, the set  is precompact in
is precompact in  . This is clear for
. This is clear for  , since
, since  . Let
. Let  be fixed and for
be fixed and for  define
define

Since  is compact for every
is compact for every  , the set
, the set  is precompact in
is precompact in  for every
for every  ,
,  Furthermore, for
Furthermore, for  we have
we have

which implies that  is totally bounded, that is, precompact in
is totally bounded, that is, precompact in  . We want to show that
. We want to show that  is an equicontinuous family of functions. For that, let
is an equicontinuous family of functions. For that, let  Then we have
Then we have

By using conditions (H2)–(H6), we get

The compactness of  implies that
implies that  is continuous in the uniform operator topology for
is continuous in the uniform operator topology for  Thus, the right hand side of (2.15) tends to zero as
Thus, the right hand side of (2.15) tends to zero as  So,
So,  is an equicontinuous family of functions. Also,
is an equicontinuous family of functions. Also,  is bounded in
is bounded in  , and so by the Arzela- Ascoli theorem,
, and so by the Arzela- Ascoli theorem,  is precompact. Hence, from the Schauder fixed point in
is precompact. Hence, from the Schauder fixed point in  any fixed point of
any fixed point of  is a mild solution of (1.1) on
is a mild solution of (1.1) on  satisfying
satisfying

Thus, system (1.1) is controllable on  .
.
3. Application
Let  be bounded with smooth boundary
be bounded with smooth boundary 
Consider the boundary control fractional integropartial differential system

The above problem can be formulated as a boundary control problem of the form of (1.1) by suitably taking the spaces  and the operators
and the operators  ,
,  and
and  as follows.
as follows.
Let  ,
,  ,
,  ,
,  , the identity operator and
, the identity operator and  ,
,  The operator
The operator  is the trace operator such that
is the trace operator such that  is well defined and belongs to
is well defined and belongs to  for each
for each  and the operator
and the operator  is given by
is given by  ,
,  where
where  and
and  are usual Sobolev spaces on
are usual Sobolev spaces on  We define the linear operator
We define the linear operator  by
by  where
where  is the unique solution to the Dirichlet boundary value problem
is the unique solution to the Dirichlet boundary value problem

We also introduce the nonlinear operator defined by

Choose  and other constants such that conditions (H1)–(H6) are satisfied. Consequently Theorem 2.2 can be applied for (3.1), so (3.1) is controllable on
and other constants such that conditions (H1)–(H6) are satisfied. Consequently Theorem 2.2 can be applied for (3.1), so (3.1) is controllable on  .
.
References
Balachandran K, Anandhi ER: Controllability of neutral functional integrodifferential infinite delay systems in Banach spaces. Taiwanese Journal of Mathematics 2004,8(4):689-702.
Balachandran K, Dauer JP, Balasubramaniam P: Controllability of nonlinear integrodifferential systems in Banach space. Journal of Optimization Theory and Applications 1995,84(1):83-91. 10.1007/BF02191736
Balachandran K, Park JY: Existence of solutions and controllability of nonlinear integrodifferential systems in Banach spaces. Mathematical Problems in Engineering 2003,2003(1-2):65-79. 10.1155/S1024123X03201022
Atmania R, Mazouzi S: Controllability of semilinear integrodifferential equations with nonlocal conditions. Electronic Journal of Differential Equations 2005,2005(75):1-9.
Balachandran K, Sakthivel R: Controllability of functional semilinear integrodifferential systems in Banach spaces. Journal of Mathematical Analysis and Applications 2001,255(2):447-457. 10.1006/jmaa.2000.7234
Balachandran K, Sakthivel R: Controllability of integrodifferential systems in Banach spaces. Applied Mathematics and Computation 2001,118(1):63-71. 10.1016/S0096-3003(00)00040-0
Balachandran K, Anandhi ER: Boundary controllability of integrodifferential systems in Banach spaces. Proceedings. Mathematical Sciences 2001,111(1):127-135. 10.1007/BF02829544
Balachandran K, Leelamani A: Boundary controllability of abstract integrodifferential systems. Journal of the Korean Society for Industrial and Applied Mathematics 2003,7(1):33-45.
El-Borai MM: Some probability densities and fundamental solutions of fractional evolution equations. Chaos, Solitons & Fractals 2002,14(3):433-440. 10.1016/S0960-0779(01)00208-9
Gorenflo R, Mainardi F: Fractional calculus and stable probability distributions. Archives of Mechanics 1998,50(3):377-388.
El-Borai MM, El-Said El-Nadi K, Mostafa OL, Ahmed HM: Semigroup and some fractional stochastic integral equations. The International Journal of Pure and Applied Mathematical Sciences 2006,3(1):47-52.
El-Borai MM, El-Said El-Nadi K, Mostafa OL, Ahmed HM: Volterra equations with fractional stochastic integrals. Mathematical Problems in Engineering 2004,2004(5):453-468. 10.1155/S1024123X04312020
El-Borai MM: The fundamental solutions for fractional evolution equations of parabolic type. Journal of Applied Mathematics and Stochastic Analysis 2004,2004(3):197-211. 10.1155/S1048953304311020
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmed, H.M. Boundary Controllability of Nonlinear Fractional Integrodifferential Systems. Adv Differ Equ 2010, 279493 (2010). https://doi.org/10.1155/2010/279493
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/279493
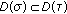 and the restriction of
and the restriction of  to
to 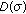 is continuous relative to the graph norm of
is continuous relative to the graph norm of 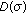 .
. is the infinitesimal generator of a compact semigroup
is the infinitesimal generator of a compact semigroup  and there exists a constant
and there exists a constant 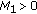 such that
such that 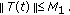
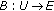 such that
such that 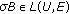 ,
,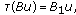 for all
for all  Also
Also  is continuously differentiable and
is continuously differentiable and 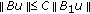 for all
for all  where C is a constant.
where C is a constant.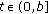 and
and 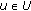 ,
, 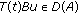 . Moreover, there exists a positive constant
. Moreover, there exists a positive constant  such that
such that 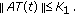
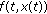 and
and 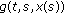 , for
, for 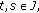 satisfy
satisfy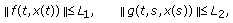
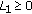 and
and 
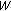 from
from 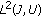 into
into 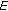 defined by
defined by