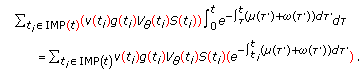- Research Article
- Open access
- Published:
On a Generalized Time-Varying SEIR Epidemic Model with Mixed Point and Distributed Time-Varying Delays and Combined Regular and Impulsive Vaccination Controls
Advances in Difference Equations volume 2010, Article number: 281612 (2010)
Abstract
This paper discusses a generalized time-varying SEIR propagation disease model subject to delays which potentially involves mixed regular and impulsive vaccination rules. The model takes also into account the natural population growing and the mortality associated to the disease, and the potential presence of disease endemic thresholds for both the infected and infectious population dynamics as well as the lost of immunity of newborns. The presence of outsider infectious is also considered. It is assumed that there is a finite number of time-varying distributed delays in the susceptible-infected coupling dynamics influencing the susceptible and infected differential equations. It is also assumed that there are time-varying point delays for the susceptible-infected coupled dynamics influencing the infected, infectious, and removed-by-immunity differential equations. The proposed regular vaccination control objective is the tracking of a prescribed suited infectious trajectory for a set of given initial conditions. The impulsive vaccination can be used to improve discrepancies between the SEIR model and its suitable reference one.
1. Introduction
Important control problems nowadays related to Life Sciences are the control of ecological models like, for instance, those of population evolution (Beverton-Holt model, Hassell model, Ricker model, etc. [1–5]) via the online adjustment of the species environment carrying capacity, that of the population growth or that of the regulated harvesting quota as well as the disease propagation via vaccination control. In a set of papers, several variants and generalizations of the Beverton-Holt model (standard time-invariant, time-varying parameterized, generalized model, or modified generalized model) have been investigated at the levels of stability, cycle-oscillatory behavior, permanence, and control through the manipulation of the carrying capacity (see, e.g., [1–5]). The design of related control actions has been proved to be important in those papers at the levels, for instance, of aquaculture exploitation or plague fighting. On the other hand, the literature about epidemic mathematical models is exhaustive in many books and papers. A nonexhaustive list of references is given in this manuscript compare [6–14] (see also the references listed therein). The sets of models include the following most basic ones [6, 7]:
-
(i)
SI-models where not removed-by-immunity population is assumed. In other words, only susceptible and infected populations are assumed,
-
(ii)
SIR-models, which include susceptible, infected, and removed-by-immunity populations,
-
(iii)
SEIR models where the infected populations are split into two ones (namely, the "infected" which incubate the disease but do not still have any disease symptoms and the "infectious" or "infective" which do exhibit the external disease symptoms).
The three above models have two possible major variants, namely, the so-called "pseudo-mass action models," where the total population is not taken into account as a relevant disease contagious factor or disease transmission power, and the so-called "true mass action models," where the total population is more realistically considered as being an inverse factor of the disease transmission rates. There are other many variants of the above models, for instance, including vaccination of different kinds: constant [8], impulsive [12], discrete-time, and so forth, by incorporating point or distributed delays [12, 13], oscillatory behaviors [14], and so forth. On the other hand, variants of such models become considerably simpler for the disease transmission among plants [6, 7]. In this paper, a mixed regular continuous-time/impulsive vaccination control strategy is proposed for a generalized time-varying SEIR epidemic model which is subject to point and distributed time-varying delays [12, 13, 15–17]. The model takes also into account the natural population growing and the mortality associated to the disease as well as the lost of immunity of newborns, [6, 7, 18] plus the potential presence of infectious outsiders which increases the total infectious numbers of the environment under study. The parameters are not assumed to be constant but being defined by piecewise continuous real functions, the transmission coefficient included [19]. Another novelty of the proposed generalized SEIR model is the potential presence of unparameterized disease thresholds for both the infected and infectious populations. It is assumed that a finite number of time-varying distributed delays might exist in the susceptible-infected coupling dynamics influencing the susceptible and infected differential equations. It is also assumed that there are potential time-varying point delays for the susceptible-infected coupled dynamics influencing the infected, infectious, and removed-by-immunity differential equations [20–22]. The proposed regulation vaccination control objective is the tracking of a prescribed suited infectious trajectory for a set of given initial conditions. The impulsive vaccination action can be used for correction of the possible discrepancies between the solutions of the SEIR model and that of its reference one due, for instance, to parameterization errors. It is assumed that the total population as well as the infectious one can be directly known by inspecting the day-to-day disease effects by directly taking the required data. Those data are injected to the vaccination rules. Other techniques could be implemented to evaluate the remaining populations. For instance, the infectious population is close to the previously infected one affected with some delay related to the incubation period. Also, either the use of the disease statistical data related to the percentages of each of the populations or the use of observers could be incorporated to the scheme to have either approximate estimations or very adjusted asymptotic estimations of each of the partial populations.
1.1. List of Main Symbols
SEIR epidemic model, namely, that consisting of four partial populations related to the disease being the susceptible, infected, infectious, and immune.
 : Susceptible population, that is, those who can be infected by the disease
: Susceptible population, that is, those who can be infected by the disease
 : Infected population, that is, those who are infected but do not still have external symptoms
: Infected population, that is, those who are infected but do not still have external symptoms
 : Infectious population, that is, those who are infected exhibiting external symptoms
: Infectious population, that is, those who are infected exhibiting external symptoms
 : Immune population
: Immune population
 : Total population
: Total population
 : Function associated with the infected floating outsiders in the SEIR model
: Function associated with the infected floating outsiders in the SEIR model
 : Disease transmission function
: Disease transmission function
 : Natural growth rate function of the population
: Natural growth rate function of the population
 : Natural rate function of deaths from causes unrelated to the infection
: Natural rate function of deaths from causes unrelated to the infection
 : Takes into account the potential immediate vaccination of new borns
: Takes into account the potential immediate vaccination of new borns
 : Functions that
: Functions that  and
and  are, respectively, the instantaneous durations per populations averages of the latent and infectious periods at time
are, respectively, the instantaneous durations per populations averages of the latent and infectious periods at time  .
.
 : the rate of lost of immunity function
: the rate of lost of immunity function
 : related to the mortality caused by the disease
: related to the mortality caused by the disease
 : Thresholds of infected and infectious populations
: Thresholds of infected and infectious populations
 : Different point and impulsive delays in the epidemic model
: Different point and impulsive delays in the epidemic model
 : Functions associated with the regular and impulsive vaccination strategies
: Functions associated with the regular and impulsive vaccination strategies
 : Weighting functions associated with distributed delays in the SEIR model.
: Weighting functions associated with distributed delays in the SEIR model.
2. Generalized True Mass Action SEIR Model with Real and Distributed Delays and Combined Regular and Impulsive Vaccination
Let  be the "susceptible" population of infection at time
be the "susceptible" population of infection at time  the "infected" (i.e., those which incubate the illness but do not still have any symptoms) at time
the "infected" (i.e., those which incubate the illness but do not still have any symptoms) at time  the "infectious" (or "infective") population at time
the "infectious" (or "infective") population at time  , and
, and  the "removed-by-immunity" (or "immune") population at time
the "removed-by-immunity" (or "immune") population at time  . Consider the extended SEIR-type epidemic model of true mass type
. Consider the extended SEIR-type epidemic model of true mass type





for all  subject to initial conditions
subject to initial conditions , and
, and  ,
,  with
with  which are absolutely continuous functions with eventual bounded discontinuities on a subset of zero measure of their definition domain and
which are absolutely continuous functions with eventual bounded discontinuities on a subset of zero measure of their definition domain and

is the maximum delay at time  of the SEIR model (2.1)–(2.4) subject to (2.5) under a potentially jointly regular vaccination action
of the SEIR model (2.1)–(2.4) subject to (2.5) under a potentially jointly regular vaccination action  and an impulsive vaccination action
and an impulsive vaccination action  at a strictly ordered finite or infinite real sequence of time instants
at a strictly ordered finite or infinite real sequence of time instants  , with
, with  being bounded and piece-wise continuous real functions used to build the impulsive vaccination term and
being bounded and piece-wise continuous real functions used to build the impulsive vaccination term and  being the indexing set of the impulsive time instants. It is assumed
being the indexing set of the impulsive time instants. It is assumed

and  which give sense of the asymptotic limit of the trajectory solutions.
which give sense of the asymptotic limit of the trajectory solutions.
The real function  in (2.5) is a perturbation in the susceptible dynamics (see, e.g., [18]) where function
in (2.5) is a perturbation in the susceptible dynamics (see, e.g., [18]) where function  , subject to the point wise constraint
, subject to the point wise constraint  , takes into account the possible decreasing in the susceptible population while increasing the infective one due to a fluctuant external infectious population entering the investigated habitat and contributing partly to the disease spread. In the above SEIR model,
, takes into account the possible decreasing in the susceptible population while increasing the infective one due to a fluctuant external infectious population entering the investigated habitat and contributing partly to the disease spread. In the above SEIR model,
-
(i)
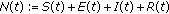 is the total population at time
is the total population at time  .
.
The following functions parameterize the SEIR model.
-
(i)
 is a bounded piecewise-continuous function related to the natural growth rate of the population.
is a bounded piecewise-continuous function related to the natural growth rate of the population. 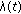 is assumed to be zero if the total population at time
is assumed to be zero if the total population at time  is less tan unity, that is,
is less tan unity, that is, 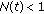 , implying that it becomes extinguished.
, implying that it becomes extinguished. -
(ii)
 is a bounded piecewise-continuous function meaning the natural rate of deaths from causes unrelated to the infection.
is a bounded piecewise-continuous function meaning the natural rate of deaths from causes unrelated to the infection. -
(iii)
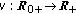 is a bounded piecewise-continuous function which takes into account the immediate vaccination of new borns at a rate
is a bounded piecewise-continuous function which takes into account the immediate vaccination of new borns at a rate 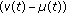 .
. -
(iv)
 is a bounded piecewise-continuous function which takes into account the number of deaths due to the infection.
is a bounded piecewise-continuous function which takes into account the number of deaths due to the infection. -
(v)
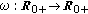 is a bounded piecewise-continuous function meaning the rate of losing immunity.
is a bounded piecewise-continuous function meaning the rate of losing immunity. -
(vi)
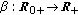 is a bounded piecewise-continuous transmission function with the total number of infections per unity of time at time
is a bounded piecewise-continuous transmission function with the total number of infections per unity of time at time  .
. -
(vii)
 is a transmission term accounting for the total rate at which susceptible become exposed to illness which replaces
is a transmission term accounting for the total rate at which susceptible become exposed to illness which replaces 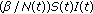 in the standard SEIR model in (2.1)–(2.2) which has a constant transmission constant
in the standard SEIR model in (2.1)–(2.2) which has a constant transmission constant 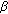 . It generalizes the one-delay distributed approach proposed in [20] for a SIRS-model with distributed delays, while it describes a transmission process weighted through a weighting function with a finite number of terms over previous time intervals to describe the process of removing the susceptible as proportional to the infectious. The functions
. It generalizes the one-delay distributed approach proposed in [20] for a SIRS-model with distributed delays, while it describes a transmission process weighted through a weighting function with a finite number of terms over previous time intervals to describe the process of removing the susceptible as proportional to the infectious. The functions  , with
, with 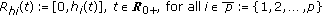 are
are  nonnegative weighting real functions being everywhere continuous on their definition domains subject to Assumption 1(1) below, and
nonnegative weighting real functions being everywhere continuous on their definition domains subject to Assumption 1(1) below, and 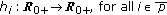 are the
are the 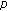 relevant delay functions describing the delay distributed-type for this part of the SEIR model. Note that a punctual delay can be modeled with a Dirac-delta distribution
relevant delay functions describing the delay distributed-type for this part of the SEIR model. Note that a punctual delay can be modeled with a Dirac-delta distribution 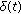 within some of the integrals and the absence of delays is modeled with all the
within some of the integrals and the absence of delays is modeled with all the  functions being identically zero.
functions being identically zero. -
(viii)
 are bounded continuous functions defined so that
are bounded continuous functions defined so that 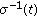 and
and  are, respectively, the instantaneous durations per populations averages of the latent and infective periods at time
are, respectively, the instantaneous durations per populations averages of the latent and infective periods at time  .
. -
(ix)
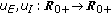 are piecewise-continuous functions being integrable on any subset of
are piecewise-continuous functions being integrable on any subset of  which are threshold functions for the infected and the infectious growing rates, respectively, which take into account (if they are not identically zero) the respective endemic populations which cannot be removed. This is a common situation for some diseases like, for instance, malaria, dengue, or cholera in certain regions where they are endemic.
which are threshold functions for the infected and the infectious growing rates, respectively, which take into account (if they are not identically zero) the respective endemic populations which cannot be removed. This is a common situation for some diseases like, for instance, malaria, dengue, or cholera in certain regions where they are endemic. -
(x)
The two following coupling infected-infectious dynamics contributions:
 (2..8)
(2..8)are single point-delay and two-point delay dynamic terms linked, respectively, to the couplings of dynamics between infected-versus-infectious populations and infectious-versus-immune populations, which take into account a single-delay effect and a double-delay effect approximating the real mutual one-stage and two-staged delayed influence between the corresponding dynamics, where
 are the gain and their associate infected and infectious delay functions which are everywhere continuous in
are the gain and their associate infected and infectious delay functions which are everywhere continuous in 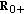 . In the time-invariant version of a simplified pseudomass-type SIRS-model proposed in [21], the constant gains are
. In the time-invariant version of a simplified pseudomass-type SIRS-model proposed in [21], the constant gains are 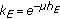 and
and 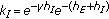 .
. -
(xi)
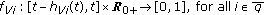 in (2.1) and (2.4) are
in (2.1) and (2.4) are 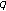 nonnegative nonidentically zero vaccination weighting real functions everywhere on their definition domains subject to distributed delays governed by the functions
nonnegative nonidentically zero vaccination weighting real functions everywhere on their definition domains subject to distributed delays governed by the functions 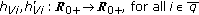 where
where 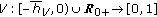 , with
, with 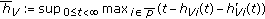 is a vaccination function to be appropriately normalized to the day-to-day population to be vaccinated subject to
is a vaccination function to be appropriately normalized to the day-to-day population to be vaccinated subject to 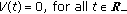 . As for the case of the transmission term, punctual delays could be included by using appropriate Dirac deltas within the corresponding integrals.
. As for the case of the transmission term, punctual delays could be included by using appropriate Dirac deltas within the corresponding integrals. -
(xii)
The SEIR model is subject to a joint regular vaccination action
 plus an impulsive one
plus an impulsive one 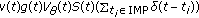 at a strictly ordered finite or countable infinite real sequence of time instants
at a strictly ordered finite or countable infinite real sequence of time instants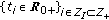 . Specifically, it is a single Dirac impulse of amplitude
. Specifically, it is a single Dirac impulse of amplitude 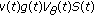 if
if  and zero if
and zero if 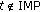 . The weighting function
. The weighting function  can be defined in several ways. For instance, if
can be defined in several ways. For instance, if 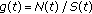 when
when 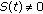 , and
, and  , otherwise, then
, otherwise, then 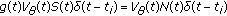 when
when 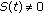 and it is zero, otherwise. Thus, the impulsive vaccination is proportional to the total population at time instants in the sequence
and it is zero, otherwise. Thus, the impulsive vaccination is proportional to the total population at time instants in the sequence 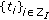 . If
. If 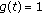 , then the impulsive vaccination is proportional to the susceptible at such time instants. The vaccination term
, then the impulsive vaccination is proportional to the susceptible at such time instants. The vaccination term  in (2.1) and (2.4) is related to a instantaneous (i.e., pulse-type) vaccination applied in particular time instants belonging to the real sequence
in (2.1) and (2.4) is related to a instantaneous (i.e., pulse-type) vaccination applied in particular time instants belonging to the real sequence  if a reinforcement of the regular vaccination is required at certain time instants, because, for instance, the number of infectious exceeds a prescribed threshold. Pulse control is an important tool in controlling certain dynamical systems [15, 23, 24] and, in particular, ecological systems, [4, 5, 25]. Pulse vaccination has gained in prominence as a result of its highly successfully application in the control of poliomyelitis and measles and in a combined measles and rubella vaccine. Note that if
if a reinforcement of the regular vaccination is required at certain time instants, because, for instance, the number of infectious exceeds a prescribed threshold. Pulse control is an important tool in controlling certain dynamical systems [15, 23, 24] and, in particular, ecological systems, [4, 5, 25]. Pulse vaccination has gained in prominence as a result of its highly successfully application in the control of poliomyelitis and measles and in a combined measles and rubella vaccine. Note that if  , then neither the natural increase of the population nor the loss of maternal lost of immunity of the newborns is taken into account. If
, then neither the natural increase of the population nor the loss of maternal lost of immunity of the newborns is taken into account. If 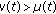 , then some of the newborns are not vaccinated with the consequent increase of the susceptible population compared to the case
, then some of the newborns are not vaccinated with the consequent increase of the susceptible population compared to the case  . If
. If 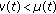 , then such a lost of immunity is partly removed by vaccinating at birth a proportion of newborns.
, then such a lost of immunity is partly removed by vaccinating at birth a proportion of newborns.
Assumption.
-
(1)
 .
. -
(2)
There exist continuous functions
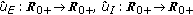 with
with 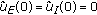 such that
such that 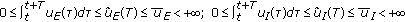 for some prefixed
for some prefixed 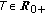 and any given
and any given 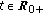 .
.
Assumption 1(1) for the distributed delay weighting functions is proposed in [20]. Assumption 1(2) implies that the infected and infectious minimum thresholds, affecting to the infected, infectious, and removed-by-immunity time derivatives, may be negative on certain intervals but their time-integrals on each interval on some fixed nonzero measure is nonnegative and bounded. This ensures that the infected and infectious threshold minimum contributions to their respective populations are always nonnegative for all time. From Picard-Lindelöff theorem, it exists a unique solution of (2.1)–(2.5) on  for each set of admissible initial conditions
for each set of admissible initial conditions  and each set of vaccination impulses which is continuous and time-differentiable on
and each set of vaccination impulses which is continuous and time-differentiable on  for time instant
for time instant  , provided that it exists, being such that
, provided that it exists, being such that  , or on
, or on  , if such a finite impulsive time instant
, if such a finite impulsive time instant  does not exist, that is, if the impulsive vaccination does not end in finite time. The solution of the generalized SEIR model for a given set of admissible functions of initial conditions is made explicit in Appendix A.
does not exist, that is, if the impulsive vaccination does not end in finite time. The solution of the generalized SEIR model for a given set of admissible functions of initial conditions is made explicit in Appendix A.
3. Positivity and Boundedness of the Total Population Irrespective of the Vaccination Law
In this section, the positivity of the solutions and their boundedness for all time under bounded non negative initial conditions are discussed. Summing up both sides on (2.1)–(2.4) yields directly

The unique solution of the above scalar equation for any given initial conditions obeys the formula

where  is the mild evolution operator which satisfies
is the mild evolution operator which satisfies  is the forcing function in (3.1). This yields the following unique solution for (3.1) for given bounded initial conditions:
is the forcing function in (3.1). This yields the following unique solution for (3.1) for given bounded initial conditions:

Consider a Lyapunov function candidate  whose time-derivative becomes
whose time-derivative becomes

Note that  , and
, and

if  .
.
Decompose uniquely any nonnegative real interval  as the following disjoint union of subintervals
as the following disjoint union of subintervals

where  are all numerable and of nonzero Lebesgue measure with the finite or infinite real sequence
are all numerable and of nonzero Lebesgue measure with the finite or infinite real sequence  of all the time instants where the time derivative of the above candidate
of all the time instants where the time derivative of the above candidate  changes its sign which are defined by construction so that the above disjoint union decomposition of the real interval
changes its sign which are defined by construction so that the above disjoint union decomposition of the real interval  is feasible for any real
is feasible for any real  , that is, if it consists of at least one element), as
, that is, if it consists of at least one element), as

Note that the identity of cardinals of sets  holds since
holds since  is the indexing set of ST and, furthermore,
is the indexing set of ST and, furthermore,
-
(a)
the sequence ST trivially exists if and only if
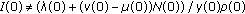 . Then,
. Then, 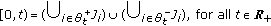 with at least one of the real interval unions being nonempty,
with at least one of the real interval unions being nonempty, 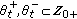 are disjoint subsets of
are disjoint subsets of  satisfying,
satisfying, 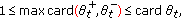 (3.8)
(3.8)and defined as follows:
-
(i)
for any given
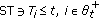 if and only if
if and only if 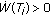 ,
, -
(ii)
for any given
 if and only if
if and only if 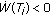 , and define also
, and define also  ,
,
-
(i)
-
(b)
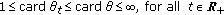 , where unit cardinal means that the time-derivative of the candidate
, where unit cardinal means that the time-derivative of the candidate  has no change of sign and infinite cardinal means that there exist infinitely many changes of sign in
has no change of sign and infinite cardinal means that there exist infinitely many changes of sign in  ,
, -
(c)
 if it exists a finite
if it exists a finite 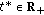 such that
such that  , and then, the sequence ST is finite (i.e., the total number of changes of sign of the time derivative of the candidate is finite) as they are the sets
, and then, the sequence ST is finite (i.e., the total number of changes of sign of the time derivative of the candidate is finite) as they are the sets 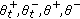 ,
, -
(d)
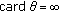 if there is no finite
if there is no finite  such that
such that 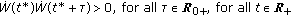 and, then, the sequence ST is infinite and the set
and, then, the sequence ST is infinite and the set  has infinite cardinal.
has infinite cardinal.
It turns out that

The following result is obtained from the above discussion under conditions which guarantee that the candidate  is bounded for all time.
is bounded for all time.
Theorem 3.1.
The total population  of the SEIR model is nonnegative and bounded for all time irrespective of the vaccination law if and only if
of the SEIR model is nonnegative and bounded for all time irrespective of the vaccination law if and only if

Remark 3.2.
Note that Theorem 3.1 may be validated since both the total population used in the construction of the candidate  and the infectious one (exhibiting explicit disease symptoms) can be either known or tightly estimated by direct inspection of the disease evolution data. Theorem 3.1 gives the most general condition of boundedness through time of the total population. It is allowed for
and the infectious one (exhibiting explicit disease symptoms) can be either known or tightly estimated by direct inspection of the disease evolution data. Theorem 3.1 gives the most general condition of boundedness through time of the total population. It is allowed for  to change through time provided that the intervals of positive derivative are compensated with sufficiently large time intervals of negative time derivative. Of course, there are simpler sufficiency-type conditions of fulfilment of Theorem 3.1 as now discussed. Assume that
to change through time provided that the intervals of positive derivative are compensated with sufficiently large time intervals of negative time derivative. Of course, there are simpler sufficiency-type conditions of fulfilment of Theorem 3.1 as now discussed. Assume that  . Thus, from (3.4):
. Thus, from (3.4):

leads to  if
if  , irrespective of
, irrespective of  since
since  is bounded, so that
is bounded, so that  and then
and then  cannot diverge what leads to a contradiction. Thus, a sufficient condition for Theorem 3.1 to hold, under the ultimate boundedness property, is that
cannot diverge what leads to a contradiction. Thus, a sufficient condition for Theorem 3.1 to hold, under the ultimate boundedness property, is that  if the infectious population is non negative through time. Another less tighter bound of the above expression for
if the infectious population is non negative through time. Another less tighter bound of the above expression for  is bounded by taking into account that
is bounded by taking into account that  as
as  since
since  if and only if
if and only if  . Then,
. Then,

what leads to  if
if  which again contradicts that
which again contradicts that  as
as  and it is a weaker condition than the above one.
and it is a weaker condition than the above one.
Note that the above condition is much more restrictive in general than that of Theorem 3.1 although easier to test.
Since the impulsive-free SEIR model (2.1)–(2.5) has a unique mild solution (then being necessarily continuous) on  , it is bounded for all finite time so that Theorem 3.1 is guaranteed under an equivalent simpler condition as follows.
, it is bounded for all finite time so that Theorem 3.1 is guaranteed under an equivalent simpler condition as follows.
Corollary 3.3.
Theorem 3.1 holds if and only if

and, equivalently,

Corollary 3.3 may also be simplified to the light of more restrictive alternative and dependent on the parameters conditions which are easier to test, as it has been made in Theorem 3.1. The following result, which is weaker than Theorem 3.1, holds.
Theorem 3.4.
Assume that
there exists  such that
such that  ,
,
and

for some constants  and some prefixed finite
and some prefixed finite  . Then, the total population
. Then, the total population  of the SEIR model is nonnegative and bounded for all time, and asymptotically extinguishes at exponential rate irrespective of the vaccination law.
of the SEIR model is nonnegative and bounded for all time, and asymptotically extinguishes at exponential rate irrespective of the vaccination law.
If the second condition is changed to

then the total population  of the SEIR model is nonnegative and bounded for all time.
of the SEIR model is nonnegative and bounded for all time.
The proof of Theorem 3.4 is given in Appendix B. The proofs of the remaining results which follow requiring mathematical proofs are also given in Appendix B. Note that the extinction condition of Theorem 3.4 is associated with a sufficiently small natural growth rate compared to the infection propagation in the case that the average immediate vaccination of new borns (of instantaneous rate ) is less than zero. Another stability result based on Gronwall's Lemma follows.
) is less than zero. Another stability result based on Gronwall's Lemma follows.
Theorem 3.5.
Assume that  exists such that
exists such that

for some prefixed finite  . Then, the total population
. Then, the total population  of the SEIR model is nonnegative and bounded for all time irrespective of the vaccination law. Furthermore,
of the SEIR model is nonnegative and bounded for all time irrespective of the vaccination law. Furthermore,  converges to zero at an exponential rate if the above second inequality is strict within some subinterval of
converges to zero at an exponential rate if the above second inequality is strict within some subinterval of  of infinite Lebesgue measure.
of infinite Lebesgue measure.
Remark 3.6.
Condition (3.17) for Theorem 3.5 can be fulfilled in a very restrictive, but easily testable fashion, by fulfilling the comparisons for the integrands for all time for the following constraints on the parametrical functions:

which is achievable, irrespective of the infectious population evolution provided that  , by vaccinating a proportion of newborns at birth what tends to decrease the susceptible population by this action compared to the typical constraint
, by vaccinating a proportion of newborns at birth what tends to decrease the susceptible population by this action compared to the typical constraint  . See Remark 3.2 concerning a sufficient condition for Theorem 3.1 to hold. Another sufficiency-type condition, alternative to (3.17), to fulfil Theorem 3.5, which involves the infectious population is
. See Remark 3.2 concerning a sufficient condition for Theorem 3.1 to hold. Another sufficiency-type condition, alternative to (3.17), to fulfil Theorem 3.5, which involves the infectious population is

Note that the infectious population is usually known with a good approximation (see Remark 3.2).
4. Positivity of the SEIR Generalized Model (2.1)–(2.5)
The vaccination effort depends on the total population and has two parts, the continuous-time one and the impulsive one (see (2.1) and (2.4)).
4.1. Positivity of the Susceptible Population of the Generalized SEIR Model
The total infected plus infectious plus removed-by-immunity populations obeys the differential equation

where



The non-negativity of any considered partial population is equivalent to the sum of the other three partial populations being less than or equal to the total population. Then, the following result holds from (3.3) and (4.1) concerning the non negative of the solution of the susceptible population for all time.
Assertion 1.
 in the SEIR generalized model (2.1)–(2.5) if and only if
in the SEIR generalized model (2.1)–(2.5) if and only if

4.2. Positivity of the Infected Population of the Generalized SEIR Model
The total susceptible plus infectious plus removed obeys the differential equation

where

Then, the following result holds concerning the non negativity of the infected population.
Assertion 2.
 if and only if
if and only if

4.3. Positivity of the Infectious Population of the Generalized SEIR Model
The total susceptible plus infected plus removed population obeys the following differential equation:

where

Thus, we have the following result concerning the non negativity of the infectious population.
Assertion 3.
 in the SEIR generalized model (2.1)–(2.5) if and only if
in the SEIR generalized model (2.1)–(2.5) if and only if

4.4. Positivity of the Removed by Immunity Population of the Generalized SEIR Model
The total numbers of susceptible, infected, and infectious populations obey the following differential equation

where

Then, the following result holds concerning the non negativity of the immune population.
Assertion 4.
 in the SEIR generalized model (2.1)–(2.5) if and only if
in the SEIR generalized model (2.1)–(2.5) if and only if

Assertions 1–4, Theorem 3.1, Corollary 3.3, and Theorems 3.4-3.5 yield directly the following combined positivity and stability theorem whose proof is direct from the above results.
Theorem 4.1.
The following properties hold.
-
(i)
If Assertions 1–4 hold jointly, then, the populations
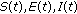 , and
, and 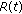 in the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by
in the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by  . If, furthermore, either Theorem 3.1, or Corollary 3.3, or Theorem 3.4 or Theorem 3.5 holds, then
. If, furthermore, either Theorem 3.1, or Corollary 3.3, or Theorem 3.4 or Theorem 3.5 holds, then 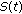 ,
, 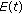 ,
, 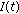 , and
, and  are bounded
are bounded 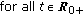 .
. -
(ii)
Assume that
for each time instant  , any three assertions among weakly formulated Assertions 1–4 hold jointly in the sense that their given statements are reformulated for such a time instant
, any three assertions among weakly formulated Assertions 1–4 hold jointly in the sense that their given statements are reformulated for such a time instant instead for all time,
instead for all time,
the three corresponding inequalities within the set of four inequalities (4.3), (4.6), (4.9), and (4.12) are, furthermore, upper bounded by  for such a time instant
for such a time instant ,
,
either Theorem 3.1, or Corollary 3.3, or Theorem 3.4 or Theorem 3.5 holds, then  ,
,  ,
,  and
and  are bounded
are bounded  .
.
Then, the populations  ,
,  ,
,  , and
, and  of the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by
of the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by  what is, in addition, bounded,
what is, in addition, bounded,  .
.
4.5. Easily Testable Positivity Conditions
The following positivity results for the solution of (2.1)–(2.4), subject to (2.5), are direct and easy to test.
Assertion 5.
Assume that  . Then,
. Then,  if and only if the conditions below hold:
if and only if the conditions below hold:
-
(a)
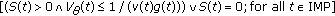 and
and -
(b)
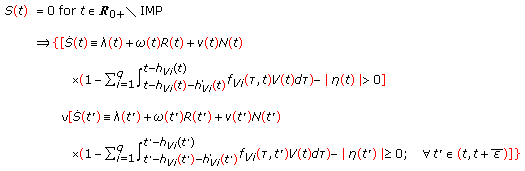 (4.13)
(4.13)
for some sufficiently small  .
.
Remark 4.2.
The positivity of the susceptible population has to be kept also in the absence of vaccination. In this way, note that if Assertion 5 holds for a given vaccination function  and a given impulsive vaccination distribution
and a given impulsive vaccination distribution  , then it also holds if those vaccination function and distribution are identically zero.
, then it also holds if those vaccination function and distribution are identically zero.
Assertion 6.
Assume that  . Then,
. Then,  if and only if
if and only if

for some sufficiently small  .
.
Assertion 7.
Assume that  . Then,
. Then,  if and only if
if and only if

for some sufficiently small  .
.
The following result follows from (2.3) and it is proved in a close way to the proof of Assertions 5–7.
Assertion 8.
Assume that  . Then,
. Then,  for any given vaccination law satisfying
for any given vaccination law satisfying  and
and  if
if

for some sufficiently small  .
.
The subsequent result is related to the first positivity interval of all the partial susceptible, infected, infectious, and immune populations under not very strong conditions requiring the (practically expected) strict positivity of the susceptible population at  , the infected-infectious threshold constraint
, the infected-infectious threshold constraint  and a time first interval monitored boundedness of the infectious population which is feasible under the technical assumption that the infection spread starts at time zero.
and a time first interval monitored boundedness of the infectious population which is feasible under the technical assumption that the infection spread starts at time zero.
Assertion 9.
Assume that
the set of absolutely continuous with eventual bounded discontinuities functions of initial conditions  satisfy, furthermore, the subsequent constraints:
satisfy, furthermore, the subsequent constraints:

 and, furthermore, it exists
and, furthermore, it exists  such that the infectious population satisfies the integral inequality,
such that the infectious population satisfies the integral inequality,

Then,  , and
, and  irrespective of the delays and vaccination laws that satisfy
irrespective of the delays and vaccination laws that satisfy  (even if the SEIR model (2.1)–(2.5) is vaccination free). Furthermore,
(even if the SEIR model (2.1)–(2.5) is vaccination free). Furthermore,  ,
, ,
, irrespective of the delays and vaccination law even if the SEIR model (2.1)–(2.5) is vaccination-free.
irrespective of the delays and vaccination law even if the SEIR model (2.1)–(2.5) is vaccination-free.
Note that  , that is, the set of impulsive time instants in
, that is, the set of impulsive time instants in  is identical to that in
is identical to that in  if and only if
if and only if  and
and  includes
includes  if and only if
if and only if  . Note also that
. Note also that  if and only if
if and only if  , in particular, if
, in particular, if  . A related result to Assertion 9 follows.
. A related result to Assertion 9 follows.
Assertion 10.
Assume that the constraints of Assertion 9 hold except that  is replaced by
is replaced by  . Then, the conclusion of Assertion 9 remains valid.
. Then, the conclusion of Assertion 9 remains valid.
A positivity result for the whole epidemic model (2.1)–(2.5) follows.
Theorem 4.3.
Assume that the SEIR model (2.1)–(2.5) under any given set of absolutely continuous initial conditions  , eventually subject to a set of isolated bounded discontinuities, is impulsive vaccination free, satisfies Assumptions 1, the constraints (4.14)–(4.16) and, furthermore,
, eventually subject to a set of isolated bounded discontinuities, is impulsive vaccination free, satisfies Assumptions 1, the constraints (4.14)–(4.16) and, furthermore,

Then, its unique mild solution is nonnegative for all time.
Theorem 4.3 is now directly extended to the presence of impulsive vaccination as follows. The proof is direct from that of Theorem 4.3 and then omitted.
Theorem 4.4.
Assume that the hypotheses of Theorem 4.3 hold and, furthermore,  such that
such that  . Then, the solution of the SEIR model (2.1)–(2.5) is nonnegative for all time.
. Then, the solution of the SEIR model (2.1)–(2.5) is nonnegative for all time.
5. Vaccination Law for the Achievement of a Prescribed Infectious Trajectory Solution
A problem of interest is the calculation of a vaccination law such that a prescribed suitable infectious trajectory solution is achieved for all time for any given set of initial conditions of the SEIR model (2.1)–(2.5). The remaining solution trajectories of the various populations in (2.1)–(2.4) are obtained accordingly. In this section, the infected trajectory is calculated so that the infectious one is the suitable one for the given initial conditions. Then, the suited susceptible trajectory is such that the infected and infectious ones are the suited prescribed ones. Finally, the vaccination law is calculated to achieve the immune population trajectory such that the above suited susceptible trajectory is calculated. In this way, the whole solution of the SEIR model is a prescribed trajectory solution which makes the infectious trajectory to be a prescribed suited one (for instance, exponentially decaying) for the given delay interval-type set of initial condition functions. The precise mathematical discussion of this topic follows through Assertions 11–13 and Theorem 5.1 below.
Assertion 11.
Consider any prescribed suitable infectious trajectory  fulfilling
fulfilling  and assume that the infected population trajectory is given by the expression:
and assume that the infected population trajectory is given by the expression:

which is in  for any susceptible trajectory
for any susceptible trajectory  under initial conditions
under initial conditions  , where the desired total population
, where the desired total population  is calculated from (3.3) as the desired population
is calculated from (3.3) as the desired population  is given by
is given by

with initial conditions being identical to those of  . Then, the infected population trajectory (5.1) guarantees the exact tracking of the infectious population of the given reference infectious trajectory
. Then, the infected population trajectory (5.1) guarantees the exact tracking of the infectious population of the given reference infectious trajectory  which furthermore satisfies the differential equation (2.3).
which furthermore satisfies the differential equation (2.3).
Assertion 12.
Assume that  and that
and that  . Consider the prescribed suitable infectious trajectory
. Consider the prescribed suitable infectious trajectory  of Assertion 11 and assume also that the infected population trajectory is given by (5.1). Then, the susceptible population trajectory given by the expression
of Assertion 11 and assume also that the infected population trajectory is given by (5.1). Then, the susceptible population trajectory given by the expression

is in  under initial conditions
under initial conditions  with
with  being given by (5.2) with initial conditions
being given by (5.2) with initial conditions  . Then, the susceptible population trajectory (5.3), subject to the infected one (5.1), guarantees the exact tracking of the infectious population of the given reference infectious trajectory
. Then, the susceptible population trajectory (5.3), subject to the infected one (5.1), guarantees the exact tracking of the infectious population of the given reference infectious trajectory  with the suited reference infected population differential equation satisfying (2.2).
with the suited reference infected population differential equation satisfying (2.2).
Assertion 13.
Assume that  and that
and that  fulfils in addition
fulfils in addition  . Assume also that
. Assume also that

Consider the prescribed suitable infectious trajectory  of Assertions 11–12 under initial conditions
of Assertions 11–12 under initial conditions  with
with  being given by (5.2) with initial conditions. Then, the vaccination law
being given by (5.2) with initial conditions. Then, the vaccination law


makes the immune population trajectory to be given by the expression


which follows from (2.1) and (A.8), such that  and
and  . Then, the immune population trajectory (5.7)-(5.8), subject to the infected one (5.1) and the susceptible one (5.3), guarantees the exact tracking of the infectious population of the given reference infectious trajectory
. Then, the immune population trajectory (5.7)-(5.8), subject to the infected one (5.1) and the susceptible one (5.3), guarantees the exact tracking of the infectious population of the given reference infectious trajectory  with the infected, susceptible, and immune population differential equations satisfying their reference ones (2.1), (2.3), and (2.4).
with the infected, susceptible, and immune population differential equations satisfying their reference ones (2.1), (2.3), and (2.4).
Note that the regular plus impulsive vaccination law (5.5)-(5.6) ensures that a suitable immune population trajectory (5.7)-(5.8) is achieved. The combination of Assertions 11–13 yields the subsequent result.
Theorem 5.1.
The vaccination law (5.5)–(5.6) makes the solution trajectory of the SEIR model (2.1)–(2.5), to be identical to the suited reference one for all time provided that their functions of initial conditions are identical.
The impulsive part of the vaccination law might be used to correct discrepancies between the SEIR model (2.1)–(2.5) and its suited reference solution due, for instance, to an imperfect knowledge of the functions parameterizing (2.1)–(2.4) which are introduced with errors in the reference model. The following result is useful in that context.
Corollary 5.2.
Assume that  for some
for some  and any given
and any given  . Then,
. Then,  (prescribed) if
(prescribed) if  with
with  so that
so that  .
.
Note that  guarantees the existence of a unique solution of (2.1)–(2.4) for each set of admissible initial conditions and a vaccination law. Corollary 5.2 is useful in practice in the following situation
guarantees the existence of a unique solution of (2.1)–(2.4) for each set of admissible initial conditions and a vaccination law. Corollary 5.2 is useful in practice in the following situation due to errors in the SEIR model (2.1)–(2.5) for some prefixed unsuitable sufficiently large
due to errors in the SEIR model (2.1)–(2.5) for some prefixed unsuitable sufficiently large  . Then, an impulsive vaccination at time
. Then, an impulsive vaccination at time  may be generated so that
may be generated so that  .
.
Extensions of the proposed methodology could include the introduction of hybrid models combining continuous-time and discrete systems and resetting systems by jointly borrowing the associate analysis of positive dynamic systems involving delays [15, 16, 26–28].
6. Simulation Example
This section contains a simulation example concerning the vaccination policy presented in Section 5. The free-vaccination evolution and then vaccination policy given in (5.5)-(5.6) are studied. The case under investigation relies on the propagation of influenza with the elementary parameterization data previously studied for a real case in [7, 29], for time-invariant delay-free SIR and SEIR models without epidemic threshold functions. In the first subsection below, the ideal case when the parameterization is fully known is investigated while in the second subsection, some extra simulations are given for the case where some parameters including certain delays are not fully known in order to investigate the robustness against uncertainties of the proposed scheme.
6.1. Ideal Case of Perfect Parameterization
The time-varying parameters of the system described by equations (2.1)–(2.4) are given by: 
 , which represent periodic oscillations around fixed values given by
, which represent periodic oscillations around fixed values given by 
 ,
,  days,
days,  (the natural growth rate is larger than the natural death rate),
(the natural growth rate is larger than the natural death rate),  days,
days,  days,
days,  , and
, and  , which means that the 80% of newborns are immediately vaccinated. The frequency is
, which means that the 80% of newborns are immediately vaccinated. The frequency is  , where the period
, where the period  , in the case of influenza, is fixed to one year. The remaining parameters are given by:
, in the case of influenza, is fixed to one year. The remaining parameters are given by:  per day,
per day,  per day,
per day,  per day,
per day,  (a constant total contribution of external infectious is assumed), and the delays
(a constant total contribution of external infectious is assumed), and the delays  days,
days,  days,
days,  days,
days,  days,
days,  days, and
days, and  days. The weighting functions are given by
days. The weighting functions are given by  ,
,  ,
,  . The initial conditions are punctual at
. The initial conditions are punctual at  with
with  , and
, and  individuals and remain constant during the interval
individuals and remain constant during the interval  days. The population evolution behavior without vaccination is depicted in Figure 1 while the total population is given by Figure 2.
days. The population evolution behavior without vaccination is depicted in Figure 1 while the total population is given by Figure 2.
As it can be appreciated from Figure 2, the total population increases slightly with time as it corresponds to a situation where the natural growth rate is larger than the combination of the natural and illness-associated death rates. As Figure 1 points out, the infectious trajectory possesses a peak value of 2713 individuals and then it stabilizes at a constant value of 1074 individuals. The goals of the vaccination policy are twofold, namely, to decrease the trajectory peak and to reduce the number of infected individuals at the steady-state.
The vaccination policy of (5.5)-(5.6) is implemented to fulfil those objectives. The desired infectious trajectory to be tracked by the vaccination law is selected as shown in Figure 3. Note that the shape of the desired trajectory is similar to the vaccination-free trajectory but with the above-mentioned goals incorporated: the peak and the steady-state values are much smaller. The partial populations are depicted in Figure 4 when the vaccination law (5.5)-(5.6) is implemented.
On one hand, the populations reach the steady-state very quick. This occurs since the desired infectious trajectory reaches the steady-state in only 10 days. On the other hand, the above-proposed goals are fulfilled as Figure 5 following on the infectious trajectory shows.
The peak in the infectious reaches only 607 individuals while the steady-state value is 65 individuals. These results are obtained with the vaccination policy depicted in Figure 6.
The vaccination effort is initially very high in order to make the system satisfies the desired infectious trajectory. Afterwards, it converges to a constant value. Moreover, note that with this vaccination strategy, the immune population increases while the susceptible, infected, and infectious reduces in comparison with the vaccination-free case. However, since the total population increases in time (Figure 2), the number of susceptible and infected individuals would also increase through time as the infectious population remains constant. In order to reduce this effect, an impulse vaccination strategy is considered. The vaccination impulses according to the law (5.6) are injected in order to increase the immune population by 100 individuals while removing the same number of individuals from the susceptible. Figures 7 and 8 display a zoom on the immune and susceptible populations when the impulsive effect is considered. The vaccination law is shown in Figure 9.
Note that the impulsive vaccination allows to improve the numbers of the immune population at chosen time instants, for instance, in cases when the total population increases through time while the disease tends to spread rapidly.
6.2. Simulations with Uncertainties
This subsection contains some numerical examples concerning the case when small uncertainties in some of the parameters of the system are present. In particular, the new values for the parameters are:  days,
days,  , and especially, the modified delays are:
, and especially, the modified delays are:  , and
, and  days. Furthermore, a small uncertainty in the initial susceptible and infected populations is considered with
days. Furthermore, a small uncertainty in the initial susceptible and infected populations is considered with  and
and  instead of 9172 and 150, respectively, taken as initial nominal values. The following Figures 10, 11, and 12 show the ideal responses for the infectious, infective, and immune and the ones obtained when the real system possesses different parameters (i.e., system with uncertainties).
instead of 9172 and 150, respectively, taken as initial nominal values. The following Figures 10, 11, and 12 show the ideal responses for the infectious, infective, and immune and the ones obtained when the real system possesses different parameters (i.e., system with uncertainties).
As it can be deduced from Figures 10, 11, and 12, the proposed vaccination strategy is robust to small uncertainties in its parameters, especially in the delays. Also, the impulsive vaccination possesses the same effect as in the example of the ideal case, that is, it increases the immune by 100 individuals at each impulsive instant and could be used to mitigate any potential deviation of the immune population due to the parameters mismatch. More technical solutions could be made for the case of presence of uncertainties, as for instance, the use of observers to estimate the state and the use of estimation-based adaptive control for the case of parametrical uncertainties.
7. Concluding Remarks
This paper has dealt with the proposal and subsequent investigation of a time-varying SEIR-type epidemic model of true mass-action type. The model includes time-varying point delays for the infected and infectious populations and distributed delays for the disease transmission effect in the model. The model also admits a potential mortality associated with the disease, a potential lost of immunity of newborns at birth, the presence of threshold population residuals in the infected and infectious populations as well as the contribution to the disease propagation in the local population of potential outsiders taking part of a floating population. A combined regular plus impulsive vaccination strategy has been proposed to remove the disease effects, the second one being used to correct major discrepancies with respect to the suitable population trajectories. The main issues have been concerned with the stability, positivity, and model-following of a suitable reference strategy via vaccination. Also, an example for the influenza disease has been given.
References
De La Sen M, Alonso-Quesada S: A control theory point of view on Beverton-Holt equation in population dynamics and some of its generalizations. Applied Mathematics and Computation 2008,199(2):464-481. 10.1016/j.amc.2007.10.021
De La Sen M, Alonso-Quesada S: Control issues for the Beverton-Holt equation in ecology by locally monitoring the environment carrying capacity: Non-adaptive and adaptive cases. Applied Mathematics and Computation 2009,215(7):2616-2633. 10.1016/j.amc.2009.09.003
De La Sen M, Alonso-Quesada S: Model-matching-based control of the Beverton-Holt equation in ecology. Discrete Dynamics in Nature and Society 2008, -21.
De La Sen M: About the properties of a modified generalized Beverton-Holt equation in ecology models. Discrete Dynamics in Nature and Society 2008, -23.
De La Sen M: The generalized Beverton-Holt equation and the control of populations. Applied Mathematical Modelling 2008,32(11):2312-2328. 10.1016/j.apm.2007.09.007
Mollison D (Ed): Epidemic Models: Their Structure and Relation to Data. Newton Institute, Cambridge University Press, New York, NY, USA; 1995.
Keeling MJ, Rohani P: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton, NJ, USA; 2008:xvi+368.
Yildirim A, Cherruault Y: Anaytical approximate solution of a SIR epidemic model with constant vaccination strategy by homotopy perturbation method. Kybernetes 2009,38(9):1566-1575. 10.1108/03684920910991540
Erturk VS, Momani S: Solutions to the problem of prey and predator and the epidemic model via differential transform method. Kybernetes 2008,37(8):1180-1188. 10.1108/03684920810884973
Ortega N, Barros LC, Massad E: Fuzzy gradual rules in epidemiology. Kybernetes 2003,32(3-4):460-477. 10.1108/03684920310463876
Khan H, Mohapatra RN, Vajravelu K, Liao SJ: The explicit series solution of SIR and SIS epidemic models. Applied Mathematics and Computation 2009,215(2):653-669. 10.1016/j.amc.2009.05.051
Song X, Jiang Y, Wei Hg: Analysis of a saturation incidence SVEIRS epidemic model with pulse and two time delays. Applied Mathematics and Computation 2009,214(2):381-390. 10.1016/j.amc.2009.04.005
Zhang T, Liu J, Teng Z: Dynamic behavior for a nonautonomous SIRS epidemic model with distributed delays. Applied Mathematics and Computation 2009,214(2):624-631. 10.1016/j.amc.2009.04.029
Mukhopadhyay B, Bhattacharyya R: Existence of epidemic waves in a disease transmission model with two-habitat population. International Journal of Systems Science 2007,38(9):699-707. 10.1080/00207720701596417
Barreiro A, Baños A: Delay-dependent stability of reset systems. Automatica 2010,46(1):216-221. 10.1016/j.automatica.2009.10.029
De La Sen M: On positivity of singular regular linear time-delay time-invariant systems subject to multiple internal and external incommensurate point delays. Applied Mathematics and Computation 2007,190(1):382-401. 10.1016/j.amc.2007.01.053
De La Sen M: Quadratic stability and stabilization of switched dynamic systems with uncommensurate internal point delays. Applied Mathematics and Computation 2007,185(1):508-526. 10.1016/j.amc.2006.07.048
Daley DJ, Gani J: Epidemic Modelling: An Introduction, Cambridge Studies in Mathematical Biology. Volume 15. Cambridge University Press, Cambridge, UK; 1999:xii+213.
Piccardi C, Lazzaris S: Vaccination policies for chaos reduction in childhood epidemics. IEEE Transactions on Biomedical Engineering 1998,45(5):591-595. 10.1109/10.668749
Zhang T, Liu J, Teng Z: Dynamic behavior for a nonautonomous SIRS epidemic model with distributed delays. Applied Mathematics and Computation 2009,214(2):624-631. 10.1016/j.amc.2009.04.029
Gao S, Teng Z, Xie Dehui: The effects of pulse vaccination on SEIR model with two time delays. Applied Mathematics and Computation 2008,201(1-2):282-292. 10.1016/j.amc.2007.12.019
Khan QJA, Krishnan EV: An epidemic model with a time delay in transmission. Applications of Mathematics 2003,48(3):193-203. 10.1023/A:1026002429257
Boichuk A, Langerová M, Škoríková J: Solutions of linear impulsive differential systems bounded on the entire real axis. Advances in Difference Equations 2010, -10.
Nieto JJ, Tisdell CC: On exact controllability of first-order impulsive differential equations. Advances in Difference Equations 2010, -9.
Yu HG, Zhong SM, Agarwal RP, Xiong LL: Species permanence and dynamical behavior analysis of an impulsively controlled ecological system with distributed time delay. Computers & Mathematics with Applications 2010,59(12):3824-3835. 10.1016/j.camwa.2010.04.018
Marchenko VM, Zachkevich Z: Representation of solutions of control hybrid differential-difference impulse systems. Differential Equations 2009,45(12):1811-1822. 10.1134/S0012266109120118
Marchenko VM, Luazo ZZ: On the stability of hybrid differential-difference systems. Differential Equations 2009,45(12):1811-1822. 10.1134/S0012266109120118
De La Sen M: A method for general design of positive real functions. IEEE Transactions on Circuits and Systems. I. Fundamental Theory and Applications 1998,45(7):764-769. 10.1109/81.703845
De La Sen M, Alonso-Quesada S: On vaccination control tools for a general SEIR-epidemic model. Proceedings of the 18th Mediterranean Conference on Control and Automation (MED '10), 2010 1: 1322-1328.
Acknowledgments
The authors thank the Spanish Ministry of Education support by Grant no. DPI2009-07197. They are also grateful to the Basque Government by its support through Grants nos. IT378-10, SAIOTEK S-PE08UN15, and SAIOTEK SPE07UN04 and SPE09UN12. The authors are very grateful to the reviewers for their useful suggestions to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Explicit Solutions of the SEIR model
A close discussion to that used to obtain the total population (3.3) from (3.1) applies for several of the remaining formulas for the nonimpulsive time instants or to the left of such instants. Assume that  are two consecutive impulsive time instants, that is,
are two consecutive impulsive time instants, that is,  . Direct calculations of the solutions of (2.1)–(2.4), subject to (2.5) and some admissible set of functions of initial conditions, yield
. Direct calculations of the solutions of (2.1)–(2.4), subject to (2.5) and some admissible set of functions of initial conditions, yield
















Proof of Theorem 3.4.
Assume with no loss in generality, since  is finite, that
is finite, that  . Note from (3.4) that if
. Note from (3.4) that if  for some
for some  so that
so that  , then
, then  for
for  , since
, since  is zero if
is zero if  . This implies that
. This implies that  . Thus, the continuity of
. Thus, the continuity of  everywhere in
everywhere in  implies that
implies that  is impossible if
is impossible if  since if
since if  is the first time instant, if any, for which
is the first time instant, if any, for which  , then
, then  . Thus, the total population is nonnegative for all time for any bounded nonnegative initial value. The combined triangle and Schwartz's inequalities used in (3.3) yield
. Thus, the total population is nonnegative for all time for any bounded nonnegative initial value. The combined triangle and Schwartz's inequalities used in (3.3) yield




and  converges to zero at an exponential rate less than any number larger than
converges to zero at an exponential rate less than any number larger than  . The second part follows from (B.2) for
. The second part follows from (B.2) for  leading to
leading to


Proof of Theorem 3.5.
Note from (3.17) and (3.3) that


for some prefixed finite  . First, rewrite (3.3) as follows:
. First, rewrite (3.3) as follows:


where


provided that  and
and  if
if  , for some real constant
, for some real constant  , since then
, since then  by hypothesis. Define
by hypothesis. Define  leading to
leading to


Then, Gronwall's lemma yields after using (B.7) that  so that
so that


which is bounded for all time provided that


Furthermore,  converges exponentially to zero if the second constraint is strict within some subinterval of
converges exponentially to zero if the second constraint is strict within some subinterval of  of infinite Lebesgue measure.
of infinite Lebesgue measure.
Proof.
The unique solution of (4.1) for given initial conditions and vaccination function is calculated by an analogous expression to (3.3) with the replacements  , and
, and  for the forcing terms,
for the forcing terms,  . Note for any
. Note for any  that
that


Substituting in the above equation the solution (3.3) of  and the equality
and the equality  for any initial conditions
for any initial conditions  , it follows that
, it follows that  for any
for any  and
and  if and only if (4.3) holds.
if and only if (4.3) holds.
Proof.
It follows from the solution (3.3) for the total population and the solution of (4.4) of  , which is obtained in a similar way as (3.3) by replacing
, which is obtained in a similar way as (3.3) by replacing  and
and  , under any initial conditions
, under any initial conditions  , it follows directly that
, it follows directly that


for any  and it follows that
and it follows that  for any
for any  and
and  which holds if and only if (4.6) holds,
which holds if and only if (4.6) holds,  .
.
Proof.
From the solution (3.3) for the total population and the solution of (4.7) of  , which is obtained in a similar way as (3.3) by replacing
, which is obtained in a similar way as (3.3) by replacing  and
and  , under any initial conditions
, under any initial conditions  , it follows directly that
, it follows directly that


for any  and it follows that
and it follows that  for any
for any  and
and  which holds if and only if (4.9) holds,
which holds if and only if (4.9) holds,  .
.
Proof.
Note that  . From (3.3) and the solution of (4.10) for any initial conditions
. From (3.3) and the solution of (4.10) for any initial conditions  , it follows that the above inequality holds if and only if
, it follows that the above inequality holds if and only if


so that  for any
for any  and
and  if and only if (4.12) holds,
if and only if (4.12) holds,  .
.
Proof.
(a) If  and
and  , then
, then  from (2.1).
from (2.1).
If  , then
, then  . Sufficiency of Conditions (a) has been proven. (b) Assume that
. Sufficiency of Conditions (a) has been proven. (b) Assume that  . Then,
. Then,  for some sufficiently small
for some sufficiently small  . Also,
. Also,  for some sufficiently small
for some sufficiently small  . As a result,
. As a result,  for some interval of time of nonzero measure and this conclusion result can be extended to the whole
for some interval of time of nonzero measure and this conclusion result can be extended to the whole  by the continuity of the solution of (2.1)–(2.5) for any set of admissible initial conditions. Sufficiency of Conditions (a)–(b) has been proven. Necessity follows directly by contradiction as follows. Assume that (a) fails for some
by the continuity of the solution of (2.1)–(2.5) for any set of admissible initial conditions. Sufficiency of Conditions (a)–(b) has been proven. Necessity follows directly by contradiction as follows. Assume that (a) fails for some  or (b) fails for some
or (b) fails for some  . Then,
. Then,


Proof.
Since  and
and  is continuous, it suffices to prove that if
is continuous, it suffices to prove that if  for some
for some  then
then  for some sufficiently small
for some sufficiently small  . This holds from (2.2) if and only if either
. This holds from (2.2) if and only if either  (guaranteed by the first part of the logic "or" of (4.14), or
(guaranteed by the first part of the logic "or" of (4.14), or  on some interval
on some interval  of nonzero measure, guaranteed by the second part of the logic "or" of (4.14), that is, if (4.14) holds. Then,
of nonzero measure, guaranteed by the second part of the logic "or" of (4.14), that is, if (4.14) holds. Then,  for
for  , some
, some  . The necessity follows by contradiction since
. The necessity follows by contradiction since  and
and  on some interval
on some interval  of nonzero measure implies the existence of
of nonzero measure implies the existence of  such that
such that  .
.
Outline of Proof of Assertion 7
Similar to the proof of Assertion 6 by using (2.3) with  and replacing
and replacing  . This guarantees
. This guarantees  at a time instant
at a time instant  or
or  within an open interval containing
within an open interval containing  if
if  . Then,
. Then,  is nonnegative for some interval
is nonnegative for some interval  if (4.15).
if (4.15).
Outline of Proof of Assertion 8
Similar to the proof of Assertion 6 by using (2.4) with  and replacing
and replacing  . This guarantees
. This guarantees  at a time instant
at a time instant  or
or  within an open interval containing
within an open interval containing  if
if  . Then,
. Then,  is nonnegative for some interval
is nonnegative for some interval  if (4.16) holds for the given regular vaccination rule. Also,
if (4.16) holds for the given regular vaccination rule. Also,  is always nonnegative since
is always nonnegative since  for any impulsive vaccination law (see (B.22) in Appendix B).
for any impulsive vaccination law (see (B.22) in Appendix B).
Proof.
Since  , and
, and  , it exist from continuity arguments
, it exist from continuity arguments  such that
such that  and
and  and
and  . All the partial populations of susceptible, infected and infectious are upper bounded by
. All the partial populations of susceptible, infected and infectious are upper bounded by  since they are nonnegative provided that
since they are nonnegative provided that  is nonnegative;
is nonnegative;  . It remains to prove that
. It remains to prove that  . It follows directly by directly calculating the unique solution of (2.4) on
. It follows directly by directly calculating the unique solution of (2.4) on  for each given set of admissible initial conditions as follows:
for each given set of admissible initial conditions as follows:


since all the coefficient functions which parameterize the SEIR model (2.1)–(2.5) and all the delay functions are bounded and either everywhere piecewise continuous or continuous on  , where
, where  is the set of impulsive time instants up till time
is the set of impulsive time instants up till time  . The above expression follows from (2.4) in a direct, but involved, way by taking into account the following facts:
. The above expression follows from (2.4) in a direct, but involved, way by taking into account the following facts:
-
(a)
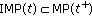 with
with  if and only if
if and only if 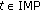 ,
, -
(b)
the solutions of (2.4) are calculated as the homogeneous solution plus the forced one for each given initial conditions in the same way as it has been made before to obtain (3.3) from (3.1) for the total population with the replacements
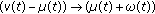 and the former forcing function by their current counterpart,
and the former forcing function by their current counterpart, -
(c)
the solution of the forced part of the solution associated with the impulsive actions is calculated as follows
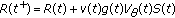 , and
, and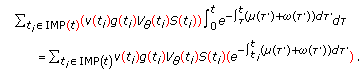 (B.16)
(B.16)
Outline of Proof of Assertion 10
The constraint  together with the remaining valid ones of Assertion 9 imply
together with the remaining valid ones of Assertion 9 imply  from (2.2) so that the proof of Assertion 9 remains valid.
from (2.2) so that the proof of Assertion 9 remains valid.
The following result gives conditions for the impulsive-free vaccination SEIR model (2.1)–(2.5) to be a positive dynamic system in the sense that any solution is nonnegative for all time under bounded absolutely continuous initial conditions  , eventually subject to a set of isolated bounded discontinuities.
, eventually subject to a set of isolated bounded discontinuities.
Proof of Theorem 4.3.
Several cases can occur, namely the following.
Case 1.
Assume that  so that
so that  does not exist. Since the unique solution of (2.1)–(2.4), subject to (2.5), is continuous on
does not exist. Since the unique solution of (2.1)–(2.4), subject to (2.5), is continuous on  for each admissible set of initial conditions
for each admissible set of initial conditions  , it follows that
, it follows that  and
and  . As a result, all the populations of the SEIR model (2.1)–(2.5) are nonnegative for all time and the result is proved for this case.
. As a result, all the populations of the SEIR model (2.1)–(2.5) are nonnegative for all time and the result is proved for this case.
Assume that  exists with
exists with  with the following potentially possible included cases.
with the following potentially possible included cases.
Case 2.
 , Then, from (2.1), Assumption 1 and the above given hypotheses,
, Then, from (2.1), Assumption 1 and the above given hypotheses,


since  , and
, and  . Then,
. Then,  for some
for some  and hence
and hence  by constructively extending the above reasoning to decompose
by constructively extending the above reasoning to decompose  as a disjoint union of real positive intervals of nonzero bounded measures, that is, Condition (b) of Assertion 5 is guaranteed provided that
as a disjoint union of real positive intervals of nonzero bounded measures, that is, Condition (b) of Assertion 5 is guaranteed provided that  .
.
Case 3.
 . One gets from (2.2)
. One gets from (2.2)


and some  if and only if (4.14) holds, that is, if and only if Assertion 6 holds so that
if and only if (4.14) holds, that is, if and only if Assertion 6 holds so that  . Then,
. Then,  provided that
provided that  .
.
Case 4.
 . If Condition (4.15) holds for
. If Condition (4.15) holds for  , then Assertion 7 holds and
, then Assertion 7 holds and  for some
for some  .
.
Case 5.
 . If the impulsive vaccination function is null and Condition (4.16) holds for
. If the impulsive vaccination function is null and Condition (4.16) holds for  , then Assertion 8 holds and
, then Assertion 8 holds and  for any positive continuous vaccination law
for any positive continuous vaccination law  for some
for some  .
.
Proof.
Replace  given by (5.1) in (2.3),
given by (5.1) in (2.3),  with
with  subject to
subject to  . Then,
. Then,  on
on  and satisfies (2.3),
and satisfies (2.3),  . Assume on the contrary that it exists a time instant
. Assume on the contrary that it exists a time instant  such that
such that  . Since
. Since  , and
, and  are everywhere continuous in
are everywhere continuous in  , it exists an open real interval
, it exists an open real interval  containing
containing  such that
such that  for a given susceptible trajectory
for a given susceptible trajectory  in such an interval satisfying (2.1) since one gets by summing-up both sides of (2.2)-(2.3) that the combined infected-infectious trajectory satisfies the differential equation
in such an interval satisfying (2.1) since one gets by summing-up both sides of (2.2)-(2.3) that the combined infected-infectious trajectory satisfies the differential equation


whose solution in  is unique for given initial conditions and forcing function. Thus,
is unique for given initial conditions and forcing function. Thus,  in
in  which leads to a contradiction.
which leads to a contradiction.
Proof.
First, note that under the given differentiability constraints of the parameterizing functions  , defined by (5.1), fulfills in addition
, defined by (5.1), fulfills in addition  . Then, the infected population trajectory given by the expression
. Then, the infected population trajectory given by the expression


 . Take (B.20) for
. Take (B.20) for  , provided that the prefixed
, provided that the prefixed  in Assertion 11 satisfies
in Assertion 11 satisfies  and
and  is calculated from (5.1) in Assertion 11,
is calculated from (5.1) in Assertion 11,  under given initial conditions
under given initial conditions  , with
, with  what implies that
what implies that  . Then, (B.20) becomes equivalently
. Then, (B.20) becomes equivalently  with the suited reference infected population differential equation satisfying (2.2) by construction.
with the suited reference infected population differential equation satisfying (2.2) by construction.
Proof.
First, note that  , defined by (5.1) and (5.3), respectively, fulfill
, defined by (5.1) and (5.3), respectively, fulfill  and
and  . The vaccination law (5.5)-(5.6) makes the immune reference trajectory (5.7)-(5.8) to be identical to the solution of (2.4) which is obtained in a similar way as (3.3) has been obtained from (3.1) for the total population by decomposing it in the solution of the homogeneous equation plus the solution of the forced part. A correcting term for the solution is added for the impulsive vaccination at impulsive time instants (see (A.7)-(A.8) in Appendix A). This leads to
. The vaccination law (5.5)-(5.6) makes the immune reference trajectory (5.7)-(5.8) to be identical to the solution of (2.4) which is obtained in a similar way as (3.3) has been obtained from (3.1) for the total population by decomposing it in the solution of the homogeneous equation plus the solution of the forced part. A correcting term for the solution is added for the impulsive vaccination at impulsive time instants (see (A.7)-(A.8) in Appendix A). This leads to




under the same initial conditions  with
with  being given by (5.2) after using Assertions 11-12.
being given by (5.2) after using Assertions 11-12.
Proof of Theorem 5.1.
The vaccination law (5.5)-(5.6) makes the immune population to track the reference one which is the unique solution of (2.4) for a given set of admissible functions of initial conditions. This one is achievable for all time by the reference susceptible population which is achievable for all time by the reference infected one (Assertions 12-13) while satisfying the differential equations (2.3), (2.4), and (2.1). The infected reference sequence is achieved by the reference infectious one for all time (Assertion 11) while satisfying the differential equation (2.2). The proof is complete from Picard-Lindeloff theorem for existence and uniqueness of the solution of (2.1)–(2.5) for each set of admissible functions of initial conditions.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M., Agarwal, R.P., Ibeas, A. et al. On a Generalized Time-Varying SEIR Epidemic Model with Mixed Point and Distributed Time-Varying Delays and Combined Regular and Impulsive Vaccination Controls. Adv Differ Equ 2010, 281612 (2010). https://doi.org/10.1155/2010/281612
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/281612
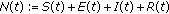 is the total population at time
is the total population at time  .
. is a bounded piecewise-continuous function related to the natural growth rate of the population.
is a bounded piecewise-continuous function related to the natural growth rate of the population. 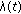 is assumed to be zero if the total population at time
is assumed to be zero if the total population at time  is less tan unity, that is,
is less tan unity, that is, 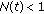 , implying that it becomes extinguished.
, implying that it becomes extinguished. is a bounded piecewise-continuous function meaning the natural rate of deaths from causes unrelated to the infection.
is a bounded piecewise-continuous function meaning the natural rate of deaths from causes unrelated to the infection.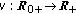 is a bounded piecewise-continuous function which takes into account the immediate vaccination of new borns at a rate
is a bounded piecewise-continuous function which takes into account the immediate vaccination of new borns at a rate 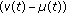 .
. is a bounded piecewise-continuous function which takes into account the number of deaths due to the infection.
is a bounded piecewise-continuous function which takes into account the number of deaths due to the infection.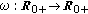 is a bounded piecewise-continuous function meaning the rate of losing immunity.
is a bounded piecewise-continuous function meaning the rate of losing immunity.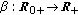 is a bounded piecewise-continuous transmission function with the total number of infections per unity of time at time
is a bounded piecewise-continuous transmission function with the total number of infections per unity of time at time  .
. is a transmission term accounting for the total rate at which susceptible become exposed to illness which replaces
is a transmission term accounting for the total rate at which susceptible become exposed to illness which replaces 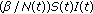 in the standard SEIR model in (2.1)–(2.2) which has a constant transmission constant
in the standard SEIR model in (2.1)–(2.2) which has a constant transmission constant 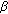 . It generalizes the one-delay distributed approach proposed in [
. It generalizes the one-delay distributed approach proposed in [ , with
, with 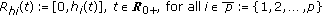 are
are  nonnegative weighting real functions being everywhere continuous on their definition domains subject to Assumption 1(1) below, and
nonnegative weighting real functions being everywhere continuous on their definition domains subject to Assumption 1(1) below, and 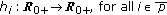 are the
are the  relevant delay functions describing the delay distributed-type for this part of the SEIR model. Note that a punctual delay can be modeled with a Dirac-delta distribution
relevant delay functions describing the delay distributed-type for this part of the SEIR model. Note that a punctual delay can be modeled with a Dirac-delta distribution 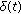 within some of the integrals and the absence of delays is modeled with all the
within some of the integrals and the absence of delays is modeled with all the  functions being identically zero.
functions being identically zero. are bounded continuous functions defined so that
are bounded continuous functions defined so that 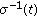 and
and  are, respectively, the instantaneous durations per populations averages of the latent and infective periods at time
are, respectively, the instantaneous durations per populations averages of the latent and infective periods at time  .
.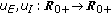 are piecewise-continuous functions being integrable on any subset of
are piecewise-continuous functions being integrable on any subset of  which are threshold functions for the infected and the infectious growing rates, respectively, which take into account (if they are not identically zero) the respective endemic populations which cannot be removed. This is a common situation for some diseases like, for instance, malaria, dengue, or cholera in certain regions where they are endemic.
which are threshold functions for the infected and the infectious growing rates, respectively, which take into account (if they are not identically zero) the respective endemic populations which cannot be removed. This is a common situation for some diseases like, for instance, malaria, dengue, or cholera in certain regions where they are endemic.
 are the gain and their associate infected and infectious delay functions which are everywhere continuous in
are the gain and their associate infected and infectious delay functions which are everywhere continuous in 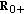 . In the time-invariant version of a simplified pseudomass-type SIRS-model proposed in [
. In the time-invariant version of a simplified pseudomass-type SIRS-model proposed in [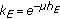 and
and 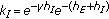 .
.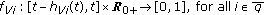 in (2.1) and (2.4) are
in (2.1) and (2.4) are 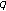 nonnegative nonidentically zero vaccination weighting real functions everywhere on their definition domains subject to distributed delays governed by the functions
nonnegative nonidentically zero vaccination weighting real functions everywhere on their definition domains subject to distributed delays governed by the functions 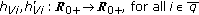 where
where 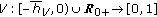 , with
, with 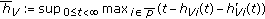 is a vaccination function to be appropriately normalized to the day-to-day population to be vaccinated subject to
is a vaccination function to be appropriately normalized to the day-to-day population to be vaccinated subject to  . As for the case of the transmission term, punctual delays could be included by using appropriate Dirac deltas within the corresponding integrals.
. As for the case of the transmission term, punctual delays could be included by using appropriate Dirac deltas within the corresponding integrals. plus an impulsive one
plus an impulsive one  at a strictly ordered finite or countable infinite real sequence of time instants
at a strictly ordered finite or countable infinite real sequence of time instants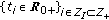 . Specifically, it is a single Dirac impulse of amplitude
. Specifically, it is a single Dirac impulse of amplitude 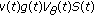 if
if  and zero if
and zero if  . The weighting function
. The weighting function  can be defined in several ways. For instance, if
can be defined in several ways. For instance, if 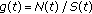 when
when 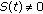 , and
, and  , otherwise, then
, otherwise, then 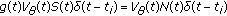 when
when 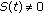 and it is zero, otherwise. Thus, the impulsive vaccination is proportional to the total population at time instants in the sequence
and it is zero, otherwise. Thus, the impulsive vaccination is proportional to the total population at time instants in the sequence 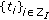 . If
. If 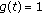 , then the impulsive vaccination is proportional to the susceptible at such time instants. The vaccination term
, then the impulsive vaccination is proportional to the susceptible at such time instants. The vaccination term  in (2.1) and (2.4) is related to a instantaneous (i.e., pulse-type) vaccination applied in particular time instants belonging to the real sequence
in (2.1) and (2.4) is related to a instantaneous (i.e., pulse-type) vaccination applied in particular time instants belonging to the real sequence  if a reinforcement of the regular vaccination is required at certain time instants, because, for instance, the number of infectious exceeds a prescribed threshold. Pulse control is an important tool in controlling certain dynamical systems [
if a reinforcement of the regular vaccination is required at certain time instants, because, for instance, the number of infectious exceeds a prescribed threshold. Pulse control is an important tool in controlling certain dynamical systems [ , then neither the natural increase of the population nor the loss of maternal lost of immunity of the newborns is taken into account. If
, then neither the natural increase of the population nor the loss of maternal lost of immunity of the newborns is taken into account. If 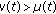 , then some of the newborns are not vaccinated with the consequent increase of the susceptible population compared to the case
, then some of the newborns are not vaccinated with the consequent increase of the susceptible population compared to the case  . If
. If 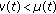 , then such a lost of immunity is partly removed by vaccinating at birth a proportion of newborns.
, then such a lost of immunity is partly removed by vaccinating at birth a proportion of newborns. .
.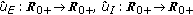 with
with 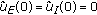 such that
such that 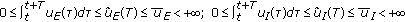 for some prefixed
for some prefixed 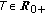 and any given
and any given  .
.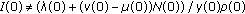 . Then,
. Then, 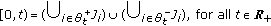 with at least one of the real interval unions being nonempty,
with at least one of the real interval unions being nonempty, 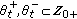 are disjoint subsets of
are disjoint subsets of  satisfying,
satisfying, 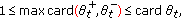
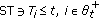 if and only if
if and only if 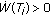 ,
, if and only if
if and only if 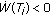 , and define also
, and define also  ,
,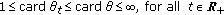 , where unit cardinal means that the time-derivative of the candidate
, where unit cardinal means that the time-derivative of the candidate  has no change of sign and infinite cardinal means that there exist infinitely many changes of sign in
has no change of sign and infinite cardinal means that there exist infinitely many changes of sign in  ,
, if it exists a finite
if it exists a finite 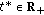 such that
such that  , and then, the sequence ST is finite (i.e., the total number of changes of sign of the time derivative of the candidate is finite) as they are the sets
, and then, the sequence ST is finite (i.e., the total number of changes of sign of the time derivative of the candidate is finite) as they are the sets 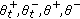 ,
,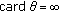 if there is no finite
if there is no finite  such that
such that 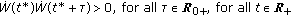 and, then, the sequence ST is infinite and the set
and, then, the sequence ST is infinite and the set  has infinite cardinal.
has infinite cardinal.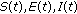 , and
, and 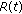 in the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by
in the generalized SEIR model (2.1)–(2.5) are lower bounded by zero and upper bounded by  . If, furthermore, either Theorem 3.1, or Corollary 3.3, or Theorem 3.4 or Theorem 3.5 holds, then
. If, furthermore, either Theorem 3.1, or Corollary 3.3, or Theorem 3.4 or Theorem 3.5 holds, then 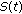 ,
, 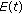 ,
, 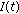 , and
, and  are bounded
are bounded 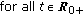 .
.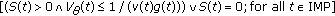 and
and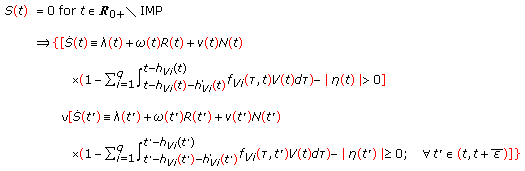












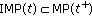 with
with  if and only if
if and only if 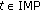 ,
,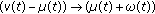 and the former forcing function by their current counterpart,
and the former forcing function by their current counterpart,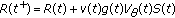 , and
, and