- Research Article
- Open access
- Published:
Inequalities among Eigenvalues of Second-Order Symmetric Equations on Time Scales
Advances in Difference Equations volume 2010, Article number: 317416 (2010)
Abstract
We consider coupled boundary value problems for second-order symmetric equations on time scales. Existence of eigenvalues of this boundary value problem is proved, numbers of their eigenvalues are calculated, and their relationships are obtained. These results not only unify the existing ones of coupled boundary value problems for second-order symmetric differential equations but also contain more complicated time scales.
1. Introduction
In this paper we consider the following second-order symmetric equation:

with the coupled boundary conditions:

where  is a time scale;
is a time scale;  and
and  are real and continuous functions in
are real and continuous functions in  over
over 
 over
over  and
and  ;
;  and
and  are the forward and backward jump operators in
are the forward and backward jump operators in  ,
,  is the delta derivative, and
is the delta derivative, and  ;
;  is a constant parameter;
is a constant parameter; 

The boundary condition (1.2) contains the two special cases: the periodic and antiperiodic conditions. In fact, (1.2) is the periodic boundary condition in the case where  and
and  the identity matrix, and (1.2) is the antiperiodic condition in the case where
the identity matrix, and (1.2) is the antiperiodic condition in the case where  and
and  Equation (1.1) with (1.2) is called a coupled boundary value problem.
Equation (1.1) with (1.2) is called a coupled boundary value problem.
Hence, according to [1, Theorem  ], the periodic and antiperiodic boundary value problems have
], the periodic and antiperiodic boundary value problems have  real eigenvalues and they satisfy the following inequality:
real eigenvalues and they satisfy the following inequality:

where  ,
,  denote the
denote the  th Dirichlet eigenvalues. Denote the number of point of a set
th Dirichlet eigenvalues. Denote the number of point of a set  by
by  and introduce the following notation for
and introduce the following notation for  :
:

Furthermore, if  , then
, then

In [2], Eastham et al. considered the second-order differential equation:

with the coupled boundary condition:

where  ,
,  ,
,  ,
,  , and
, and  ,
,  ,
,  ,
,  ,
,  a.e. on
a.e. on  . Here
. Here  denote the set of real number, and
denote the set of real number, and  the space of real valued Lebesgue integrable functions on
the space of real valued Lebesgue integrable functions on  . They obtained the following results: the coupled boundary value problem (1.7) with (1.8) has an infinite but countable number of only real eigenvalues which can be ordered to form a nondecreasing sequence:
. They obtained the following results: the coupled boundary value problem (1.7) with (1.8) has an infinite but countable number of only real eigenvalues which can be ordered to form a nondecreasing sequence:

In the present paper, we try to extend these results on time scales. We shall remark that Eastham et al. employed continuous eigenvalue branch which studied in [2], in their proof. Instead, we will make use of some oscillation results that are extended from the results obtained by Agarwal et al. [4] to prove the existence of eigenvalues of (1.1) with (1.2) and compare the eigenvalues as  varies.
varies.
This paper is organized as follows. Section 2 introduces some basic concepts and fundamental theory about time scales and gives some properties of eigenvalues of a kind of separated boundary value problem for (1.1) which will be used in Section 4. Our main result has been introduced in Section 3. Section 4 pays attention to prove some propositions, by which one can easily obtain the existence and the comparison result of eigenvalues of the coupled boundary value problems (1.1) with (1.2). By using these propositions, we give the proof of our main result in Section 5.
2. Preliminaries
In this section, some basic concepts and some fundamental results on time scales are introduced. Next, the eigenvalues of the kind of separated boundary value problem for (1.1) and the oscillation of their eigenfunction are studied. Finally, the reality of the eigenvalues of the coupled boundary value problems for (1.1) is shown.
Let  be a nonempty closed subset. Define the forward and backward jump operators
be a nonempty closed subset. Define the forward and backward jump operators  by
by

where  ,
,  . A point
. A point  is called right-scattered, right-dense, left-scattered, and left-dense if
is called right-scattered, right-dense, left-scattered, and left-dense if  , and
, and  respectively.
respectively.
We assume throughout the paper that if 0 is right-scattered, then it is also left-scattered, and if 1 is left-scattered, then it is also right-scattered.
Since  is a nonempty bounded closed subset of
is a nonempty bounded closed subset of  , we put
, we put  . The graininess
. The graininess  is defined by
is defined by

Let  be a function defined on
be a function defined on  .
.  is said to be (delta) differentiable at
is said to be (delta) differentiable at  provided there exists a constant
provided there exists a constant  such that for any
such that for any  , there is a neighborhood
, there is a neighborhood  of
of  (i.e.,
(i.e.,  for some
for some  ) with
) with

In this case, denote  . If
. If  is (delta) differentiable for every
is (delta) differentiable for every  , then
, then  is said to be (delta) differentiable on
is said to be (delta) differentiable on  . If
. If  is differentiable at
is differentiable at  , then
, then

If  for all
for all  , then
, then  is called an antiderivative of
is called an antiderivative of  on
on  . In this case, define the delta integral by
. In this case, define the delta integral by

Moreover, a function  defined on
defined on  is said to be rd-continuous if it is continuous at every right-dense point in
is said to be rd-continuous if it is continuous at every right-dense point in  and its left-sided limit exists at every left-dense point in
and its left-sided limit exists at every left-dense point in  .
.
For convenience, we introduce the following results ([5, Chapter 1], [6, Chapter 1], and [7, Lemma  ]), which are useful in the paper.
]), which are useful in the paper.
Lemma 2.1.
Let  and
and  .
.
-
(i)
If
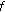 is differentiable at
is differentiable at 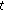 , then
, then 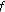 is continuous at
is continuous at 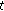 .
. -
(ii)
If
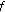 and
and 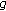 are differentiable at
are differentiable at  , then
, then 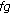 is differentiable at
is differentiable at  and
and 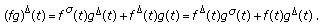 (26)
(26)
-
(iii)
If
 and
and 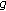 are differentiable at
are differentiable at  , and
, and 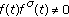 , then
, then  is differentiable at
is differentiable at 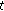 and
and 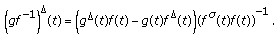 (27)
(27)
-
(iv)
If
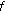 is rd-continuous on
is rd-continuous on 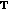 , then it has an antiderivative on
, then it has an antiderivative on  .
.
Now, we turn to discuss some properties of solutions of (1.1) and eigenvalues of its boundary value problems.
Define the Wronskian by

where  is the set of twice differentiable functions with rd-continuous second derivative. The following result can be derived from the Lagrange Identity [5, Theorem
is the set of twice differentiable functions with rd-continuous second derivative. The following result can be derived from the Lagrange Identity [5, Theorem  ].
].
Lemma 2.2.
For any two solutions  and
and  of (1.1),
of (1.1),  is a constant on
is a constant on  .
.
In [4], Agarwal et al. studied the following second-order symmetric linear equation:

with the boundary conditions:

where  is continuous;
is continuous;  ;
;  satisfy that if
satisfy that if  is right-scattered, then it is also left-scattered; and if
is right-scattered, then it is also left-scattered; and if  is left-scattered, then it is also right-scattered. A solution
is left-scattered, then it is also right-scattered. A solution  of (2.9) is said to have a node at
of (2.9) is said to have a node at  if
if  . A generalized zero of
. A generalized zero of  is defined as its zero or its node. Without loss of generality, they assumed that
is defined as its zero or its node. Without loss of generality, they assumed that  and
and  in (2.10) satisfy
in (2.10) satisfy
(H) and
and
and obtained the following oscillation result.
Lemma 2.3 (see [4, Theorem  ]).
]).
The eigenvalues of (2.9) with (2.10) may be arranged as  and an eigenfunction corresponding to
and an eigenfunction corresponding to  has exactly
has exactly  -generalized zeros in the open interval
-generalized zeros in the open interval  .
.
In order to study the kind of separated boundary value problem for (1.1), we now extend the above oscillation theorem to the more general equation (1.1) with

By  denote the number of generalized zeros of the solution
denote the number of generalized zeros of the solution  of (1.1) with the initial conditions
of (1.1) with the initial conditions

in the open interval (0,1), where  and
and  satisfy
satisfy  with
with  and
and  replaced by
replaced by  and
and  , respectively. It can be easily verified that
, respectively. It can be easily verified that

which is independent of  .
.
Lemma 2.4 (see [1, Lemma  ]).
]).
Let  be the solution of (1.1) with (2.12). Then
be the solution of (1.1) with (2.12). Then  is strictly decreasing in
is strictly decreasing in  for each
for each  whenever
whenever 
Lemma 2.5 (see [1, Lemma  ]).
]).
If there exists  such that
such that  , then
, then  for all
for all 
With a similar argument to that used in the proof of [4, Theorem  ], one can show the following result.
], one can show the following result.
Theorem 2.6.
All the eigenvalues of (1.1) with (2.11) are simple and can be arranged as  and an eigenfunction corresponding to
and an eigenfunction corresponding to  has exactly
has exactly  -generalized zeros in the open interval
-generalized zeros in the open interval  , where
, where  satisfy that if
satisfy that if  is right-scattered, then it is also left-scattered; if
is right-scattered, then it is also left-scattered; if  is left-scattered, then it is also right-scattered. Furthermore, the number of its eigenvalues is equal to
is left-scattered, then it is also right-scattered. Furthermore, the number of its eigenvalues is equal to  .
.
Setting  ,
,  , and
, and  in (2.11), where
in (2.11), where  ,
,  are elements of
are elements of  in (1.2), we get the following separated boundary conditions:
in (1.2), we get the following separated boundary conditions:

The following result is a direct consequence of Theorem 2.6.
Theorem 2.7.
All the eigenvalues of (1.1) with (2.14) are simple and can be arranged as

and an eigenfunction corresponding to  has exactly
has exactly  -generalized zeros in
-generalized zeros in  Furthermore, the number of its eigenvalues is equal to
Furthermore, the number of its eigenvalues is equal to  .
.
For convenience, we shall write  if
if 
Lemma 2.8.
For each  ,
, 

Proof.
The proof is similar to that of [4, Theorem  ]. So the details are omitted.
]. So the details are omitted.
Lemma 2.9.
All the eigenvalues of the coupled boundary value problem (1.1) with (1.2) are real.
Proof.
The proof is similar to that of [1, Lemma  ]. So the details are omitted.
]. So the details are omitted.
3. Main Result
In this section we state our main results: general inequalities among eigenvalues of coupled boundary value problem of (1.1) with (1.2).
Theorem 3.1.
If  and
and  or
or  and
and  , then, for every fixed
, then, for every fixed  ,
,  , coupled boundary value problem (1.1) with (1.2) has
, coupled boundary value problem (1.1) with (1.2) has  eigenvalues and these eigenvalues satisfy the following inequalities:
eigenvalues and these eigenvalues satisfy the following inequalities:

where  . Furthermore, if
. Furthermore, if  then
then

Remark 3.2.
If  and
and  or
or  and
and  , a similar result can be obtained by applying Theorem 3.1 to
, a similar result can be obtained by applying Theorem 3.1 to  . In fact,
. In fact,  for
for  and
and  for
for  . Hence, the boundary condition (1.2) in the cases of
. Hence, the boundary condition (1.2) in the cases of  or
or  and
and  , can be written as condition (1.2), where
, can be written as condition (1.2), where  is replaced by
is replaced by  for
for  and
and  for
for  , and
, and  is replaced by
is replaced by  .
.
4. The Characteristic Function 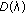
Before showing Theorem 3.1, we need to prove the following six propositions.
Let  and
and  be the solutions of (1.1) satisfying the following initial conditions:
be the solutions of (1.1) satisfying the following initial conditions:

respectively. Obviously,  and
and  are two linearly independent solutions of (1.1). By Lemma 2.2 we have
are two linearly independent solutions of (1.1). By Lemma 2.2 we have

which, together with the assumption of  , implies
, implies

For any fixed  ,
,  , and all
, and all  , we define
, we define






Note that

Let

Hence, we have

and by Lemma 2.2, we get

Proposition 4.1.
For  ,
,  is an eigenvalue of (1.1) with (1.2) if and only if
is an eigenvalue of (1.1) with (1.2) if and only if

Moreover,  is a multiple eigenvalue of (1.1) with (1.2) if and only if
is a multiple eigenvalue of (1.1) with (1.2) if and only if

Proof.
Since  and
and  are linearly independent solutions of (1.1), then
are linearly independent solutions of (1.1), then  is an eigenvalue of the problem (1.1) with (1.2) if and only if there exist two constants
is an eigenvalue of the problem (1.1) with (1.2) if and only if there exist two constants  and
and  , not both zero, such that
, not both zero, such that  satisfies (1.2), which yields
satisfies (1.2), which yields

It is evident that (4.15) has a nontrivial solution  if and only if
if and only if

which together with (4.3), (4.4) and  implies that
implies that

It follows from the above relation and the fact that  that
that  is an eigenvalue of (1.1) with (1.2) if and only if
is an eigenvalue of (1.1) with (1.2) if and only if  satisfies
satisfies

On the other hand, (1.1) has two linearly independent solutions satisfying (1.2) if and only if all the entries of the coefficient matrix of (4.16) are zero. Hence,  is a multiple eigenvalue of (1.1) with (1.2) if and only if (4.15) holds. This completes the proof.
is a multiple eigenvalue of (1.1) with (1.2) if and only if (4.15) holds. This completes the proof.
The following result is a direct consequence of the first result of Proposition 4.1.
Corollary 4.2.
For any  ,
,

For  and
and  , we consider the separated boundary problem (1.1) with (2.14). Let
, we consider the separated boundary problem (1.1) with (2.14). Let  , be all the eigenvalues of (1.1) with (2.14) and ordered as that in Theorem 2.7. Since
, be all the eigenvalues of (1.1) with (2.14) and ordered as that in Theorem 2.7. Since  and
and  are all entire functions in
are all entire functions in  for each
for each  ,
,  is an entire functions in
is an entire functions in  . Denote
. Denote

Proposition 4.3.
Assume that  and
and  or
or  and
and  . For each
. For each  ,
,  if
if  is odd, and
is odd, and  if
if  is even.
is even.
Proof.
It is noted that  is eigenvalue of (1.1) with (2.14) if and only if
is eigenvalue of (1.1) with (2.14) if and only if  . Hence,
. Hence,  is an eigenfunction with respect to
is an eigenfunction with respect to  . By Theorem 2.7 and the last two relations in (4.1), we have that
. By Theorem 2.7 and the last two relations in (4.1), we have that  has exactly
has exactly  generalized zeros in
generalized zeros in  and
and

-
(i)
If
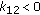 , then it follows from
, then it follows from 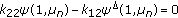 that
that 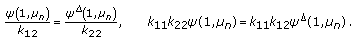 (423)
(423)
By (4.3) and the first relation in (4.23) we have

By the definition of  , the second relation in (4.23), and
, the second relation in (4.23), and  , we get
, we get

Hence,

Noting  ,
,  , and (4.22), we have that if
, and (4.22), we have that if  is odd, then
is odd, then

and if  is even, then
is even, then

-
(ii)
If
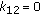 , then it is noted that
, then it is noted that 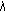 is eigenvalue of (1.1) with (2.14) if and only if
is eigenvalue of (1.1) with (2.14) if and only if  Hence,
Hence, 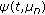 is an eigenfunction with respect to
is an eigenfunction with respect to 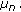 By Theorem 2.7,
By Theorem 2.7,  has exactly
has exactly  generalized zeros in
generalized zeros in 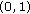 and
and 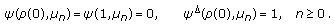 (429)
(429)
Hence  for all
for all 
Next we will show  In the case that
In the case that  ,
,  and
and  It follows from (1.1) and (2.4) that
It follows from (1.1) and (2.4) that

which implies

In the other case that  , then
, then

Further, by the existence and uniqueness theorem of solutions of initial value problems for (1.1) [5, Theorem  ], we obtain that
], we obtain that 
With a similar argument from above, we get sgn
By referring to  and from (4.3), it follows that
and from (4.3), it follows that

Hence, noting  and
and  , if
, if  is odd, then
is odd, then

and if  is even, then
is even, then

This completes the proof.
Proposition 4.4.
Assume that  and
and  or
or  and
and  . There exists a constant
. There exists a constant  such that
such that  and
and  .
.
Proof.
Since  and
and  are solutions of (1.1), we have
are solutions of (1.1), we have

By integration, it follows from (4.1) and (4.36) that

where  is used. In addition, from (4.36), we obtain
is used. In addition, from (4.36), we obtain

which, similarly together with (4.1) and by integration, imply that

On the other hand, it follows from Lemma 2.5 and (4.1) that for all sufficiently large  ,
,  ,
,  , for all
, for all  , where
, where  and
and  in (2.11) are taken as
in (2.11) are taken as  ,
,  , and
, and  ,
,  , respectively, which satisfy
, respectively, which satisfy  . So, from (4.37) and (4.39), we obtain that
. So, from (4.37) and (4.39), we obtain that

and by Lemma 2.4, it implies

By Proposition 4.3,  . Therefore, there exists a
. Therefore, there exists a  such that
such that  . This completes the proof.
. This completes the proof.
Lemma 4.5.
For any  one has
one has



Proof.
Since  and
and  are solutions of (1.1) with (4.1), then they satisfy (4.36). Differentiating (4.36) with respect to
are solutions of (1.1) with (4.1), then they satisfy (4.36). Differentiating (4.36) with respect to  , we have
, we have

By the variation of constants formula [5, Theorem  ], we get
], we get

Further, it follows from [5, Theorem  ] that
] that

From (4.46), (4.47), and (4.11), we have

where

It follows from (4.11) and (4.13) that

where 
Hence,

By (4.10) and (4.12), we have

Differentiating above relation with respect to  , and with (4.12), we have
, and with (4.12), we have

which together with (4.10) confirm (4.42).
To establish (4.43), from (4.12) and (4.10), we obtain

Thus

That is, (4.43) holds. The identity (4.44) can be verified similarly. This completes the proof.
Corollary 4.6.
If  satisfies
satisfies  , then
, then  ,
,  , and
, and  .
.
Proof.
These are direct consequences of (4.43) and (4.44).
Lemma 4.7.
 if and only if
if and only if  for some
for some  and
and  is an eigenfunction of
is an eigenfunction of  .
.
Proof.
It is directly follows from the definition of  and the initial conditions (4.1).
and the initial conditions (4.1).
Lemma 4.8.
Assum that  or
or  and
and  is a multiple eigenvalue of (1.1) with (1.2) if and only if
is a multiple eigenvalue of (1.1) with (1.2) if and only if  .
.
Proof.
Assume that  . By (4.15)
. By (4.15)  is a multiple eigenvalue if and only if
is a multiple eigenvalue if and only if

hence, it follows from (4.12) that

Therefore  and
and 
(i)Suppose that  is a multiple eigenvalue of (1.1) with (1.2). Then
is a multiple eigenvalue of (1.1) with (1.2). Then  and
and  By (4.42),
By (4.42),  .
.
(ii)Suppose that  is an eigenvalue of (1.1) with (1.2) and
is an eigenvalue of (1.1) with (1.2) and  . Then by (4.14),
. Then by (4.14),  . From (4.43) and (4.44) we get
. From (4.43) and (4.44) we get

Since  and
and  are linearly independence solutions of (1.1), we have
are linearly independence solutions of (1.1), we have

It follows from  and
and  that
that  . Thus,
. Thus,  is a multiple eigenvalue of (1.1) with (1.2).
is a multiple eigenvalue of (1.1) with (1.2).
The case  can be established by replacing
can be established by replacing  by
by  in the above argument. This completes the proof.
in the above argument. This completes the proof.
Lemma 4.9.
Assume  or
or  . If
. If  is a multiple eigenvalue of (1.1) with (1.2), then there exists
is a multiple eigenvalue of (1.1) with (1.2), then there exists  such that
such that  .
.
Proof.
Assume that  is a multiple eigenvalue of (1.1) with (1.2). From the proof of Lemma 4.8 we see that
is a multiple eigenvalue of (1.1) with (1.2). From the proof of Lemma 4.8 we see that  . From (4.9) we have
. From (4.9) we have

This means that  for some
for some  This completes the proof.
This completes the proof.
Proposition 4.10.
Assume that  and
and  or
or  and
and  .
.
-
(i)
Equations
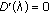 and
and  or
or 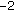 hold if and only if
hold if and only if 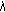 is a multiple eigenvalue of (1.1) with (1.2) with
is a multiple eigenvalue of (1.1) with (1.2) with 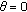 or
or 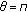 .
. -
(ii)
If
 or
or 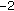 and
and 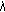 is a multiple eigenvalue of (1.1) with (1.2), then
is a multiple eigenvalue of (1.1) with (1.2), then 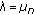 ,
, 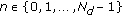 .
. -
(iii)
If
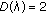 or
or 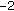 for some
for some 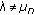 ,
,  , then
, then 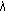 is a simple eigenvalue of (1.1) with (1.2) with
is a simple eigenvalue of (1.1) with (1.2) with 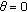 or
or 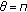 .
. -
(iv)
Moreover, for every
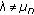 ,
,  , with
, with 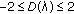 one has
one has  (461)
(461)
and in the case of  ,
,

Proof.
Parts (i), (ii), and (iii) follow from Lemmas 4.8 and 4.9. It follows from Propositions 4.3 and 4.4 and Corollary 4.6 that  ,
,  with
with  and
and  when
when  . Hence,
. Hence,  with
with  ,
,  . Similarly, by Proposition 4.3 and Corollary 4.6, we have
. Similarly, by Proposition 4.3 and Corollary 4.6, we have

which implies

If  , then all the points of
, then all the points of  are isolated. In this case, (1.1) can be rewritten as
are isolated. In this case, (1.1) can be rewritten as

where

By Theorem 2.7, (1.1) with (2.14) has  eigenvalues:
eigenvalues:

It follows from (4.65) that  and
and  are two polynomials of degree
are two polynomials of degree  in
in  and
and  and
and  are two polynomials of degree
are two polynomials of degree  in
in  . Then
. Then  can be written as
can be written as

where  and
and  is a polynomial in
is a polynomial in  whose order is not larger than
whose order is not larger than  . By Proposition 4.3, if
. By Proposition 4.3, if  is odd, then
is odd, then  , and if
, and if  is even, then
is even, then  . It follows that if
. It follows that if  is odd, then
is odd, then  as
as  and if
and if  is even, then
is even, then  as
as  . Hence, if
. Hence, if  is odd, then there exists a constant
is odd, then there exists a constant  such that
such that  . Similarly, in the other case that
. Similarly, in the other case that  is even, there exists a constant
is even, there exists a constant  such that
such that  , and by using Corollary 4.6, we have
, and by using Corollary 4.6, we have

Hence,

This completes the proof.
Proposition 4.11.
For any fixed  ,
,  , each eigenvalue of (1.1) with (1.2) is simple.
, each eigenvalue of (1.1) with (1.2) is simple.
Proof.
It follows from (4.46) and (4.47) that

where

Then from (4.1),  , and the definition of
, and the definition of  , we have
, we have

Thus, if  , then
, then  .
.  is always positive semidefinite or negative semidefinite. Consequently,
is always positive semidefinite or negative semidefinite. Consequently,  is not change sign in
is not change sign in  . In this case,
. In this case,  cannot vanish unless
cannot vanish unless  . Because
. Because  and
and  are linearly independent,
are linearly independent,  if and only if all the entries of the matrix
if and only if all the entries of the matrix  vanish, namely,
vanish, namely,

Suppose that  is an eigenvalue of the problem (1.1) with (1.2) and fix
is an eigenvalue of the problem (1.1) with (1.2) and fix  with
with  . By Proposition 4.1, we have
. By Proposition 4.1, we have  , then
, then  , and the matrix
, and the matrix  is positive definite or negative definite. Hence,
is positive definite or negative definite. Hence,  or
or  for
for  , since
, since  and
and  are linearly independent.
are linearly independent.
If  is a multiple eigenvalue of problem (1.1) with (1.2), then (4.15) holds by Proposition 4.1. By using (4.15), it can be easily verified that (4.74) holds; that is, all the entries of the matrix
is a multiple eigenvalue of problem (1.1) with (1.2), then (4.15) holds by Proposition 4.1. By using (4.15), it can be easily verified that (4.74) holds; that is, all the entries of the matrix  are zeros. Then
are zeros. Then  , which is contrary to
, which is contrary to  . Hence,
. Hence,  is a simple eigenvalue of (1.1) and (1.2). This completes the proof.
is a simple eigenvalue of (1.1) and (1.2). This completes the proof.
Proposition 4.12.
If  is odd,
is odd,  , and
, and  then
then  ; if
; if  is even,
is even,  , and
, and  then
then  .
.
Proof.
Assume  and
and  with
with  being odd. It follows from Proposition 4.1 that
being odd. It follows from Proposition 4.1 that

As in the proof of Lemma 4.5 and by (4.11) and (4.13),

Hence,

where (4.51) is used and

by the Holder inequality [8, Lemma  (iv)]. Therefore
(iv)]. Therefore  . Since
. Since  and
and  are linearly independent, which proves the first conclusion, the second conclusion can be shown similarly. This completes the proof.
are linearly independent, which proves the first conclusion, the second conclusion can be shown similarly. This completes the proof.
5. Proofs of the Main Results
Proof of Theorem 3.1.
By Propositions 4.1–4.12 and the intermediate value theorem, the inequalities in (3.1)–(3.2) can been illustrated with the graph of  (see Figures 1–3). We now give the detail proof of Theorem 3.1. By Lemma 2.9, all the eigenvalues of the coupled boundary value problem (1.1) with (1.2) are real. By Propositions 4.3–4.10,
(see Figures 1–3). We now give the detail proof of Theorem 3.1. By Lemma 2.9, all the eigenvalues of the coupled boundary value problem (1.1) with (1.2) are real. By Propositions 4.3–4.10,  ,
,  for all
for all  with
with  and there exists
and there exists  such that
such that  Therefore, by the continuity of
Therefore, by the continuity of  and the intermediate value theorem, (1.1) and (1.2) with
and the intermediate value theorem, (1.1) and (1.2) with  have only one eigenvalue
have only one eigenvalue  , (1.1) and (1.2) with
, (1.1) and (1.2) with  hve only one eigenvalue
hve only one eigenvalue  , and (1.1) and (1.2) with
, and (1.1) and (1.2) with  ,
,  have only one eigenvalue
have only one eigenvalue  , and they satisfy
, and they satisfy

Similarly, by Propositions 4.1, 4.3, and 4.10, the continuity of  and the intermediate value theorem,
and the intermediate value theorem,  reaches
reaches  ,
,  (
( ,
,  ), and
), and  exactly one time between any two consecutive eigenvalues of the separated boundary value problem (1.1) with (2.14). Hence, (1.1) and (1.2) with
exactly one time between any two consecutive eigenvalues of the separated boundary value problem (1.1) with (2.14). Hence, (1.1) and (1.2) with  ,
,  ,
,  , and
, and  have only one eigenvalue between any two consecutive eigenvalues of (1.1) with (2.14), respectively. In addition, by Propositions 4.10 and 4.12, if
have only one eigenvalue between any two consecutive eigenvalues of (1.1) with (2.14), respectively. In addition, by Propositions 4.10 and 4.12, if  or
or  and
and  , then
, then  is not only an eigenvalue of (1.1) with (2.14) but also a multiple eigenvalue of (1.1) and (1.2) with
is not only an eigenvalue of (1.1) with (2.14) but also a multiple eigenvalue of (1.1) and (1.2) with  and
and  .
.
If  , then it follows from the above discussion that (1.1) and (1.2) with
, then it follows from the above discussion that (1.1) and (1.2) with  ,
,  have infinitely many eigenvalues, and they are real and satisfy (3.1).
have infinitely many eigenvalues, and they are real and satisfy (3.1).
If  , then all points of
, then all points of  are isolated. In this case (1.1) and
are isolated. In this case (1.1) and  can be rewritten as (4.65) and (4.68). By the same method in the proof of Proposition 4.10, that if
can be rewritten as (4.65) and (4.68). By the same method in the proof of Proposition 4.10, that if  is even, then there exists a constant
is even, then there exists a constant  such that
such that  , which together with (4.62), implies that (1.1) and (1.2) with
, which together with (4.62), implies that (1.1) and (1.2) with  ,
,  ,
,  , and
, and  have only one eigenvalue
have only one eigenvalue  ,
,  , and
, and  , satisfying
, satisfying

(see Figure 2). Similarly, in the other case that  is even, there exists a constant
is even, there exists a constant  such that
such that  which, together with (4.62) implies that (1.1) and (1.2) with
which, together with (4.62) implies that (1.1) and (1.2) with  ,
,  ,
,  , and
, and  have only one eigenvalue
have only one eigenvalue  ,
,  , and
, and  , satisfying
, satisfying

(see Figure 3). Therefore, we get that (1.1) and (1.2) with  ,
,  have
have  eigenvalues and they are real and satisfy
eigenvalues and they are real and satisfy

if  is odd; and
is odd; and

if  is even. This completes the proof.
is even. This completes the proof.
Remark 5.1.
In the continuous case:  ,
,  , by Theorem 3.1, the coupled boundary value problems (1.1) and (1.2) have infinitely many eigenvalues:
, by Theorem 3.1, the coupled boundary value problems (1.1) and (1.2) have infinitely many eigenvalues:  for
for  ,
,  ;
;  for
for  ;
;  for
for  , and they satisfy inequality (3.1). This result is the same as that obtained by Eastham et al. for second-order differential equations [2, Theorem
, and they satisfy inequality (3.1). This result is the same as that obtained by Eastham et al. for second-order differential equations [2, Theorem  ].
].
Example 5.2.
Consider the following three specific cases:

It is evident that  and then
and then  in these three cases. By Theorem 3.1, the coupled boundary value problems (1.1) and (1.2) have infinitely many real eigenvalues and they satisfy the inequality (3.1). Obviously, the above three cases are not continuous and not discrete. So the existing results are not available now.
in these three cases. By Theorem 3.1, the coupled boundary value problems (1.1) and (1.2) have infinitely many real eigenvalues and they satisfy the inequality (3.1). Obviously, the above three cases are not continuous and not discrete. So the existing results are not available now.
By Remark 5.1 and Example 5.2, our result in Theorem 3.1 not only extends the results in the discrete cases but also contains more complicated time scales.
References
Zhang C, Shi Y: Eigenvalues of second-order symmetric equations on time scales with periodic and antiperiodic boundary conditions. Applied Mathematics and Computation 2008,203(1):284-296. 10.1016/j.amc.2008.04.044
Eastham MSP, Kong Q, Wu H, Zettl A: Inequalities among eigenvalues of Sturm-Liouville problems. Journal of Inequalities and Applications 1999,3(1):25-43.
Everitt WN, Möller M, Zettl A:Discontinuous dependence of the
 -th Sturm-Liouville eigenvalue. In General Inequalities, 7. Volume 123. Birkhäuser, Basel, Switzerland; 1997:145-150.
-th Sturm-Liouville eigenvalue. In General Inequalities, 7. Volume 123. Birkhäuser, Basel, Switzerland; 1997:145-150.Agarwal RP, Bohner M, Wong PJY: Sturm-Liouville eigenvalue problems on time scales. Applied Mathematics and Computation 1999,99(2-3):153-166. 10.1016/S0096-3003(98)00004-6
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Lakshmikantham V, Sivasundaram S, Kaymakcalan B: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:x+285.
Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Bohner M, Lutz DA: Asymptotic behavior of dynamic equations on time scales. Journal of Difference Equations and Applications 2001,7(1):21-50. 10.1080/10236190108808261
Acknowledgments
Many thanks to A. Pankov (the Editor) and the anonymous reviewer(s) for helpful comments and suggestions. This research was supported by the Natural Science Foundation of Shandong Province (Grant Y2008A28) (Grant ZR2009AL003) and the Natural Science Fund Project of the University of Jinan (Grant XKY0918).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, C., Sun, S. Inequalities among Eigenvalues of Second-Order Symmetric Equations on Time Scales. Adv Differ Equ 2010, 317416 (2010). https://doi.org/10.1155/2010/317416
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/317416
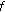 is differentiable at
is differentiable at 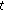 , then
, then 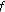 is continuous at
is continuous at 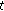 .
.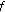 and
and 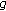 are differentiable at
are differentiable at  , then
, then 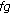 is differentiable at
is differentiable at  and
and 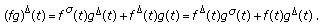
 and
and 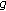 are differentiable at
are differentiable at  , and
, and 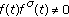 , then
, then  is differentiable at
is differentiable at 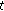 and
and 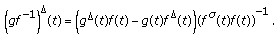
 is rd-continuous on
is rd-continuous on  , then it has an antiderivative on
, then it has an antiderivative on  .
.
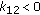 , then it follows from
, then it follows from 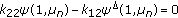 that
that 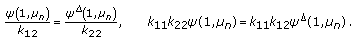
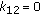 , then it is noted that
, then it is noted that 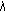 is eigenvalue of (1.1) with (2.14) if and only if
is eigenvalue of (1.1) with (2.14) if and only if  Hence,
Hence, 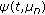 is an eigenfunction with respect to
is an eigenfunction with respect to 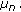 By Theorem 2.7,
By Theorem 2.7,  has exactly
has exactly  generalized zeros in
generalized zeros in 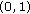 and
and 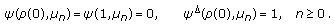
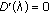 and
and  or
or 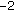 hold if and only if
hold if and only if 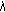 is a multiple eigenvalue of (1.1) with (1.2) with
is a multiple eigenvalue of (1.1) with (1.2) with 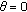 or
or 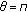 .
. or
or 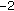 and
and 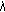 is a multiple eigenvalue of (1.1) with (1.2), then
is a multiple eigenvalue of (1.1) with (1.2), then 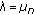 ,
, 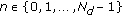 .
.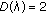 or
or 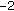 for some
for some 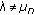 ,
,  , then
, then 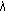 is a simple eigenvalue of (1.1) with (1.2) with
is a simple eigenvalue of (1.1) with (1.2) with 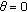 or
or 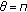 .
.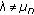 ,
,  , with
, with 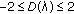 one has
one has 

 .
.
 in the case that
in the case that  is odd.
is odd.
 in the case that
in the case that  is even.
is even. -th Sturm-Liouville eigenvalue. In General Inequalities, 7. Volume 123. Birkhäuser, Basel, Switzerland; 1997:145-150.
-th Sturm-Liouville eigenvalue. In General Inequalities, 7. Volume 123. Birkhäuser, Basel, Switzerland; 1997:145-150.