- Research Article
- Open access
- Published:
Pairs of Function Spaces and Exponential Dichotomy on the Real Line
Advances in Difference Equations volume 2010, Article number: 347670 (2010)
Abstract
We provide a complete diagram of the relation between the admissibility of pairs of Banach function spaces and the exponential dichotomy of evolution families on the real line. We prove that if  and
and  are two Banach function spaces with the property that either
are two Banach function spaces with the property that either  or
or  , then the admissibility of the pair
, then the admissibility of the pair  implies the existence of the exponential dichotomy. We study when the converse implication holds and show that the hypotheses on the underlying function spaces cannot be dropped and that the obtained results are the most general in this topic. Finally, our results are applied to the study of exponential dichotomy of
implies the existence of the exponential dichotomy. We study when the converse implication holds and show that the hypotheses on the underlying function spaces cannot be dropped and that the obtained results are the most general in this topic. Finally, our results are applied to the study of exponential dichotomy of  -semigroups.
-semigroups.
1. Introduction
In the study of the asymptotic behavior of evolution equations the input-output conditions are very efficient tools, with wide applicability area, and give a nice connection between control theory and the qualitative theory of differential equations (see [1–16] and the reference therein). Starting with the pioneering work of Perron (see [8]) these methods were developed and improved in remarkable books (see [1, 4, 6]). A new and interesting perspective on this framework was proposed in [5], where the authors presented a complete study of stability, expansiveness, and dichotomy of evolution families on the half-line in terms of input-output methods. This paper was the starting point for an entire collection of studies dedicated to the input-output techniques and their applications to the qualitative theory of differential and difference equations.
If one analyzes the dichotomous properties of differential equations, then it is easily seen that there are some main technical differences between the case of evolution families on the half-line (see [5, 9, 10]) and the case of evolution families on the real line (see [11–16]), which require a distinct analysis for each case. For instance, when one determines sufficient conditions for the existence of exponential dichotomy on the half-line, an important hypothesis is that the initial stable subspace is closed and complemented (see, e.g., [5, Theorem 4.3] or [9, Theorem 3.3]). This assumption may be dropped when we study the exponential dichotomy on the real line (see, e.g., [11, Theorem 5.1] or [16, Theorem 5.3]). These facts implicitly generate the differences between the admissibility concepts used on the real line compared with those used on the half-line and also interesting technical approaches in each case.
The aim of the present paper is to provide new and very general conditions for the existence of exponential dichotomy on the real line. We consider the problem of finding connections between the solvability of an integral equation and the existence of exponential dichotomy of evolution families on the real line. The main purpose is to obtain a complete diagram and a classification of the classes of function spaces that may be used in the study of exponential dichotomy via admissibility.
For the beginning we will present the previous results in this topic and the main objectives will be clearly specified in the context of the actual state of knowledge. We denote by  the class of all Banach sequence spaces
the class of all Banach sequence spaces  which are invariant under translations, contain the continuous functions with compact support, satisfy an integral property and if
which are invariant under translations, contain the continuous functions with compact support, satisfy an integral property and if  , then there is a continuous function
, then there is a continuous function  . We consider
. We consider  the subclass of
the subclass of  satisfying the ideal property. We associate two subclasses of
satisfying the ideal property. We associate two subclasses of  :
:  —the class of all Banach function spaces with unbounded fundamental function and
—the class of all Banach function spaces with unbounded fundamental function and  —the class of all Banach function spaces which contain at least a nonintegrable function. A pair of function spaces
—the class of all Banach function spaces which contain at least a nonintegrable function. A pair of function spaces  is called admissible for an evolution family
is called admissible for an evolution family  on the Banach space
on the Banach space  if for every test function in the input space
if for every test function in the input space  there exists a unique solution function in the output space
there exists a unique solution function in the output space  for the associated integral equation given by the variation of constants formula (see Definition 3.5 below).
for the associated integral equation given by the variation of constants formula (see Definition 3.5 below).
For the first time, we have proposed in [11] a sufficient condition for exponential dichotomy, using certain Banach function spaces which are invariant under translations and we obtained the following theorem.
Theorem 1.1.
If  and the pair
and the pair  is admissible for an evolution family
is admissible for an evolution family  , then
, then  is exponentially dichotomic.
is exponentially dichotomic.
Our study has been continued and extended in [16], both for uniform dichotomy and exponential dichotomy. According to the proof of Theorem 4.8 in [16] we may give the following sufficient condition for uniform dichotomy.
Theorem 1.2.
If  ,
,  , and the pair
, and the pair  is admissible for an evolution family
is admissible for an evolution family  , then
, then  is uniformly dichotomic.
is uniformly dichotomic.
From the proof of Theorem 5.3(i) in [16] we deduce the following sufficient condition for exponential dichotomy.
Theorem 1.3.
If  ,
,  , and the pair
, and the pair  is admissible for an evolution family
is admissible for an evolution family  , then
, then  is exponentially dichotomic.
is exponentially dichotomic.
Taking into account the above results and their consequences, the natural question arises whether, in the general case, the output space may belong to the class  and if so, which is the most general class where the input space should belong to. The aim of the present paper is to answer this question and to provide a complete study of the exponential dichotomy on the real line via integral admissibility. The answer to the above question will establish clearly how should one modify the hypotheses of Theorem 1.2 such that the admissibility of the pair
and if so, which is the most general class where the input space should belong to. The aim of the present paper is to answer this question and to provide a complete study of the exponential dichotomy on the real line via integral admissibility. The answer to the above question will establish clearly how should one modify the hypotheses of Theorem 1.2 such that the admissibility of the pair  implies the existence of the exponential dichotomy.
implies the existence of the exponential dichotomy.
We will prove that if  and
and  , then the admissibility of the pair
, then the admissibility of the pair  is a sufficient condition for exponential dichotomy. Consequently, we will deduce a complete diagram of the study of exponential dichotomy on the real line in terms of the admissibility of function spaces (see Theorem 3.11). Specifically, if
is a sufficient condition for exponential dichotomy. Consequently, we will deduce a complete diagram of the study of exponential dichotomy on the real line in terms of the admissibility of function spaces (see Theorem 3.11). Specifically, if  and
and  are two Banach function spaces with the property that either
are two Banach function spaces with the property that either  or
or  , then the admissibility of the pair
, then the admissibility of the pair  implies the existence of the exponential dichotomy. Also, in certain conditions, we deduce that the exponential dichotomy of an evolution family
implies the existence of the exponential dichotomy. Also, in certain conditions, we deduce that the exponential dichotomy of an evolution family  is equivalent with the admissibility of the pair
is equivalent with the admissibility of the pair  .
.
By an example we motivate our techniques and show that the hypotheses from our main results cannot be removed. Precisely, if  and
and  are such that
are such that  and
and  , then we prove that the admissibility of the pair
, then we prove that the admissibility of the pair  does not imply the exponential dichotomy. Moreover, we show that the obtained results and their consequences are the most general in this topic.
does not imply the exponential dichotomy. Moreover, we show that the obtained results and their consequences are the most general in this topic.
Finally, our results are applied at the study of the exponential dichotomy of  -semigroups. Using function spaces which are invariant under translations, we obtain a classification of the classes of input and output spaces which may be used in the study of exponential dichotomy of semigroups in terms of input-output techniques with respect to associated integral equations.
-semigroups. Using function spaces which are invariant under translations, we obtain a classification of the classes of input and output spaces which may be used in the study of exponential dichotomy of semigroups in terms of input-output techniques with respect to associated integral equations.
2. Preliminaries: Banach Function Spaces
In this section, for the sake of clarity, we present some definitions and notations and we introduce the main classes of function spaces that will be used in our study. Let  be the linear space of all Lebesgue measurable functions
be the linear space of all Lebesgue measurable functions  , identifying the functions equal almost everywhere.
, identifying the functions equal almost everywhere.
Definition 2.1.
A linear subspace  of
of  is called normed function space if there is a mapping
is called normed function space if there is a mapping  such that
such that
-
(i)
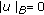 if and only if
if and only if  a.e.;
a.e.; -
(ii)
 , for all
, for all  ;
; -
(iii)
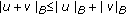 , for all
, for all 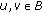 ;
; -
(iv)
if
 and
and 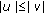 a.e. then
a.e. then 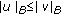 ;
; -
(v)
if
 , then
, then 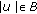 .
.
If  is complete, then
is complete, then  is called Banach function space.
is called Banach function space.
Definition 2.2.
A Banach function space  is said to be invariant under translations if for every
is said to be invariant under translations if for every  , the function
, the function  belongs to
belongs to  and
and  .
.
Notations 1.
Let  denote the linear space of all continuous functions
denote the linear space of all continuous functions  with compact support. Throughout this paper, we denote by
with compact support. Throughout this paper, we denote by  the class of all Banach function spaces
the class of all Banach function spaces  , which are invariant under translations,
, which are invariant under translations,  , and satisfy the following conditions:
, and satisfy the following conditions:
-
(i)
for every
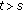 there is
there is 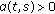 such that
such that  , for all
, for all  ;
; -
(ii)
if
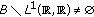 then there is a continuous function
then there is a continuous function 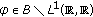 .
.
For examples of Banach function spaces from the class  we refer to [11].
we refer to [11].
Let  be the class of all Banach function spaces
be the class of all Banach function spaces  with the property that if
with the property that if  a.e. and
a.e. and  , then
, then  .
.
For every  we denote by
we denote by  the characteristic function of the set
the characteristic function of the set  . Then, if
. Then, if  , we have that
, we have that  , for every
, for every  with
with  .
.
Definition 2.3.
Let  . The mapping
. The mapping  is called the fundamental function of the space
is called the fundamental function of the space  .
.
For the proof of the next proposition we refer to [16, Proposition 2.8].
Proposition 2.4.
Let  and
and  . If
. If  is a function, which belongs to
is a function, which belongs to  and with the property that
and with the property that  belongs to
belongs to  , then the functions
, then the functions

belong to  .
.
Example 2.5.
Let  be the linear space of all
be the linear space of all  with the property that
with the property that  . With respect to the norm
. With respect to the norm

this is a Banach function space which belongs to  .
.
Lemma 2.6.
If  , then
, then  .
.
Proof.
Let  be such that
be such that  , for all
, for all  . Then, we have that
. Then, we have that

Notations 2.
In what follows we denote by
-
(i)
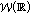 the class of all Banach function spaces
the class of all Banach function spaces 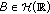 with
with 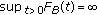 ;
; -
(ii)
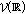 the class of all Banach function spaces
the class of all Banach function spaces  with the property that
with the property that 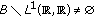 ;
; -
(iii)
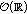 the class of all Banach function spaces
the class of all Banach function spaces 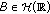 with the property that for every
with the property that for every  in
in 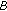 , the function
, the function  belongs to
belongs to  .
.
Remark 2.7.
-
(i)
For examples of Banach function spaces from the class
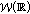 we refer to [16, Proposition 2.9].
we refer to [16, Proposition 2.9]. -
(ii)
If
 then there is a continuous function
then there is a continuous function  with
with 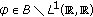 .
.
Notation 1.
Let  be the space of all continuous functions
be the space of all continuous functions  with
with  , which is Banach space with respect to the norm
, which is Banach space with respect to the norm  .
.
Lemma 2.8.
Let  be a Banach function space with
be a Banach function space with  . Then
. Then  .
.
Proof.
Let  . Let
. Let  . Then there is an unbounded increasing sequence
. Then there is an unbounded increasing sequence  such that
such that  , for all
, for all  and all
and all  . Setting
. Setting  we have that
we have that

From the above inequality we deduce that  is fundamental in the Banach space
is fundamental in the Banach space  , so there is
, so there is  such that
such that  in
in  . According to [16, Lemma 2.4] there is a subsequence
. According to [16, Lemma 2.4] there is a subsequence  such that
such that  a.e. This implies that
a.e. This implies that  a.e., so
a.e., so  in
in  . Thus
. Thus  and the proof is complete.
and the proof is complete.
Notation 2.
Let  be a real or complex Banach space. For every
be a real or complex Banach space. For every  we denote by
we denote by  the linear space of all Bochner measurable functions
the linear space of all Bochner measurable functions  with the property that the mapping
with the property that the mapping  lies in
lies in  . With respect to the norm
. With respect to the norm  ,
,  is a Banach space.
is a Banach space.
3. Exponential Dichotomy for Evolution Families on the Real Line
Let  be a real or complex Banach space. The norm on
be a real or complex Banach space. The norm on  and on
and on  , the Banach algebra of all bounded linear operators on
, the Banach algebra of all bounded linear operators on  , will be denoted by
, will be denoted by  . Denote by
. Denote by  the identity operator on
the identity operator on  . First, we remind some basic definitions.
. First, we remind some basic definitions.
Definition 3.1.
A family  of bounded linear operators on
of bounded linear operators on  is called an evolution family if the following properties hold:
is called an evolution family if the following properties hold:
-
(i)
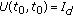 and
and 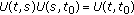 , for all
, for all 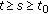 ;
; -
(ii)
for every
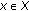 and every
and every 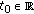 the mapping
the mapping 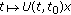 is continuous on
is continuous on 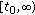 and the mapping
and the mapping  is continuous on
is continuous on 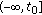 ;
; -
(iii)
there are
 and
and  such that
such that 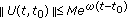 , for all
, for all  .
.
Definition 3.2.
An evolution family  is said to be uniformly dichotomic if there are a family of projections
is said to be uniformly dichotomic if there are a family of projections  and a constant
and a constant  such that
such that
-
(i)
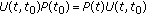 , for all
, for all 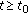 ;
; -
(ii)
the restriction
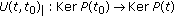 is an isomorphism, for all
is an isomorphism, for all  ;
; -
(iii)
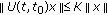 , for all
, for all 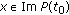 and all
and all  ;
; -
(iv)
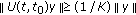 , for all
, for all  and all
and all 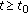 .
.
Definition 3.3.
An evolution family  is said to be exponentially dichotomic if there exist a family of projections
is said to be exponentially dichotomic if there exist a family of projections  and two constants
and two constants  and
and  such that
such that
-
(i)
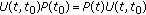 , for all
, for all 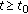 ;
; -
(ii)
the restriction
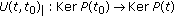 is an isomorphism, for all
is an isomorphism, for all 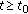 ;
; -
(iii)
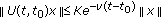 , for all
, for all 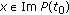 and all
and all 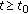 ;
; -
(iv)
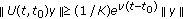 , for all
, for all  and all
and all 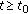 .
.
Remark 3.4.
It is obvious that if an evolution family is exponentially dichotomic, then it is uniformly dichotomic.
One of the most efficient tool in the study of the dichotomic behavior of an evolution family is represented by the so-called input-output techniques. The input-output method considered in this paper is the admissibility of a pair of function spaces. Indeed, let  be two Banach function spaces such that
be two Banach function spaces such that  and
and  .
.
Definition 3.5.
The pair  is said to be admissible for
is said to be admissible for  if for every
if for every  there exists a unique
there exists a unique  such that the pair
such that the pair  satisfies the equation
satisfies the equation

Remark 3.6.
If the pair  is admissible for
is admissible for  , then it makes sense to define the operator
, then it makes sense to define the operator  , where
, where  is such that the pair
is such that the pair  satisfies (). Then
satisfies (). Then  is a bounded linear operator (see [16, Proposition 4.4]).
is a bounded linear operator (see [16, Proposition 4.4]).
Let  be an evolution family on
be an evolution family on  and
and  . For every
. For every  , we consider the stable subspace
, we consider the stable subspace as the space of all
as the space of all  with the property that the function
with the property that the function

belongs to  and we define the unstable subspace
and we define the unstable subspace as the space of all
as the space of all  with the property that there is a function
with the property that there is a function  such that
such that  and
and  , for all
, for all  .
.
An important information concerning the structure of the projection family associated with a uniformly dichotomic evolution family was obtained in [16, Theorem 4.8] and this is given by the following.
Theorem 3.7.
Let  be an evolution family on
be an evolution family on  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If the pair
. If the pair  is admissible for the evolution family
is admissible for the evolution family  , then
, then  is uniformly dichotomic with respect to the family of projections
is uniformly dichotomic with respect to the family of projections  , where
, where

Taking into account the results obtained in [11, 16], an interesting open question is whether in the study of exponential dichotomy, the output space may belong to the general class  . To answer this question, the first purpose of this paper is to prove the following theorem.
. To answer this question, the first purpose of this paper is to prove the following theorem.
Theorem 3.8.
Let  be an evolution family on the Banach space
be an evolution family on the Banach space  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If the pair
. If the pair  is admissible for
is admissible for  , then
, then  is uniformly exponentially dichotomic.
is uniformly exponentially dichotomic.
The proof will be constructive and therefore, we will present several intermediate results.
Theorem 3.9.
Let  be an evolution family on the Banach space
be an evolution family on the Banach space  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If the pair
. If the pair  is admissible for
is admissible for  , then there are
, then there are  such that
such that

Proof.
According to Theorem 3.7 and Definition 3.2(iii) we have that there is  such that
such that

Since  , from Remark 2.7(ii) we have that there is a continuous function
, from Remark 2.7(ii) we have that there is a continuous function  with
with  . Using the invariance under translations of the space
. Using the invariance under translations of the space  , we may assume that there is
, we may assume that there is  such that
such that

Since  there is
there is  such that
such that

Let  be a continuous function with
be a continuous function with  and
and  , for
, for  . Then, the function
. Then, the function  is continuous and from (3.5) and (3.6) we have that
is continuous and from (3.5) and (3.6) we have that

Let  and let
and let  . We consider the functions
. We consider the functions


Since  it follows that
it follows that  . Setting
. Setting  we observe that
we observe that  , for all
, for all  . Since
. Since  we deduce that
we deduce that  . A simple computation shows that the pair
. A simple computation shows that the pair  satisfies (), so
satisfies (), so  . This implies that
. This implies that

According to relation (3.4) we observe that

and using the invariance under translations of the space  we deduce that
we deduce that 
 . From
. From  , for all
, for all  , we have that
, we have that  . Thus we obtain that
. Thus we obtain that

From  , for all
, for all  , we have that
, we have that  , for all
, for all  , which implies that
, which implies that

Setting  , from relations (3.10)–(3.13) it follows that
, from relations (3.10)–(3.13) it follows that

Using relations (3.7) and (3.14) we deduce that  Taking into account that
Taking into account that  does not depend on
does not depend on  or
or  , we have that
, we have that

Let  and
and  . Let
. Let  and
and  . Then, there are
. Then, there are  and
and  such that
such that  . Using relations (3.4) and (3.15) we obtain that
. Using relations (3.4) and (3.15) we obtain that  , which completes the proof.
, which completes the proof.
Theorem.
Let  be an evolution family on the Banach space
be an evolution family on the Banach space  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If the pair
. If the pair  is admissible for
is admissible for  , then there are
, then there are  such that
such that

Proof.
Let  and
and  be given by Definition 3.1. According to Theorem 3.7 and Definition 3.2(iv) we have that there is
be given by Definition 3.1. According to Theorem 3.7 and Definition 3.2(iv) we have that there is  such that
such that

Since  , from Remark 2.7(ii) we have that there is a continuous function
, from Remark 2.7(ii) we have that there is a continuous function  with
with  . Using the invariance under translations of the space
. Using the invariance under translations of the space  we may assume that there is
we may assume that there is  such that
such that

Using similar arguments with those in the proof of Theorem 3.9 we obtain that there is a continuous function  with
with  ,
,  , for all
, for all  and
and

Let  and
and  . Then, there is
. Then, there is  such that
such that  and
and  , for all
, for all  . We consider the functions
. We consider the functions


where  . We have that
. We have that  , so
, so  . Using relation (3.17) we have that
. Using relation (3.17) we have that

From this inequality, since  we deduce that
we deduce that  . An easy computation shows that the pair
. An easy computation shows that the pair  satisfies (), so
satisfies (), so  . Then, we have that
. Then, we have that

Using relation (3.17) we have that

which implies that

Since  , for all
, for all  , we deduce that
, we deduce that

This shows that

From relations (3.19)–(3.27) it follows that  . Taking into account that
. Taking into account that  does not depend on
does not depend on  or
or  , we have that
, we have that

We set  and
and  . Let
. Let  and
and  . Then, there are
. Then, there are  and
and  such that
such that  . Using relations (3.17) and (3.28) we obtain that
. Using relations (3.17) and (3.28) we obtain that  , which completes the proof.
, which completes the proof.
Now, we may give the proof of Theorem 3.8.
Proof of Theorem 3.8.
This immediately follows from Theorems 3.7, 3.9, and 3.10.
Now, we may give the main result of the paper, which establishes a complete diagram concerning the study of exponential dichotomy on the real line in terms of integral admissibility.
Theorem 3.11.
Let  be an evolution family on the Banach space
be an evolution family on the Banach space  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If
. If  or
or  , then the following assertions hold:
, then the following assertions hold:
-
(i)
if the pair
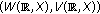 is admissible for
is admissible for 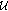 , then
, then 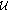 is uniformly exponentially dichotomic;
is uniformly exponentially dichotomic; -
(ii)
if
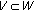 and one of the spaces
and one of the spaces 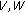 belongs to the class
belongs to the class 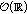 , then
, then 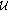 is exponentially dichotomic if and only if the pair
is exponentially dichotomic if and only if the pair 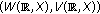 is admissible for
is admissible for  .
.
Proof.
-
(i)
This follows from Theorems 1.3 and 3.8.
-
(ii)
Necessity. Suppose that
 is exponentially dichotomic with respect to the family of projections
is exponentially dichotomic with respect to the family of projections 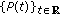 and the constants
and the constants 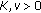 . Then, we have that
. Then, we have that 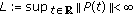 (see, e.g., [13]).
(see, e.g., [13]).
Let  . We consider the function
. We consider the function

where for every  ,
,  denotes the inverse of the operator
denotes the inverse of the operator  .
.
If  , then using Proposition 2.4 we obtain that
, then using Proposition 2.4 we obtain that  . Since
. Since  we deduce that
we deduce that  .
.
If  then, since
then, since  we have that
we have that  . Using Proposition 2.4 it follows that
. Using Proposition 2.4 it follows that  .
.
An easy computation shows that the pair  satisfies (). The uniqueness of
satisfies (). The uniqueness of  is immediate (see, e.g., [16, the Necessity part of Theorem 5.3]). In conclusion, the pair
is immediate (see, e.g., [16, the Necessity part of Theorem 5.3]). In conclusion, the pair  is admissible for the evolution family
is admissible for the evolution family  .
.
The natural question arises whether the hypotheses from Theorem 3.11 can be dropped and also if the conditions given by this theorem are the most general in this topic. The answers are given by the following example.
Example 3.12.
Let  and
and  be such that
be such that  and
and  . Then
. Then  and according to Lemma 2.8 we have that
and according to Lemma 2.8 we have that  .
.
We consider the function

Then  is a decreasing function.
is a decreasing function.
Let  endowed with the norm
endowed with the norm  , for all
, for all  . For every
. For every  we consider the operator
we consider the operator

Then  is an evolution family on
is an evolution family on  .
.
We prove that the pair  is admissible for
is admissible for  . Let
. Let  . Then
. Then  . We consider the function
. We consider the function

We have that  is correctly defined and an easy computation shows that the pair
is correctly defined and an easy computation shows that the pair  satisfies (). We set
satisfies (). We set

We prove that  . Since
. Since  , from
, from

we have that  . Let
. Let  . Then, there is
. Then, there is  such that
such that  . It follows that
. It follows that

The above inequality implies that  . Since
. Since  was arbitrary we obtain that there exists
was arbitrary we obtain that there exists  . Using similar arguments with those in (3.34) we deduce that
. Using similar arguments with those in (3.34) we deduce that  .
.
Let  . Then there is
. Then there is  such that
such that  . It follows that
. It follows that

From this inequality we have that  . Since
. Since  was arbitrary, it follows that there exists
was arbitrary, it follows that there exists  . Thus, we deduce that
. Thus, we deduce that  , so
, so  .
.
To prove the uniqueness of  , let
, let  be such that the pair
be such that the pair  satisfies (). Setting
satisfies (). Setting  we have that
we have that  and
and  , for all
, for all  . If
. If  , then we deduce that
, then we deduce that


Let  . Using Lemma 2.6 and integrating in (3.37) we have that
. Using Lemma 2.6 and integrating in (3.37) we have that

For  in (3.39) we obtain that
in (3.39) we obtain that  .
.
From relation (3.38) we have that

Integrating in relation (3.40) on  and using Lemma 2.6, we deduce that
and using Lemma 2.6, we deduce that

For  in (3.41) it follows that
in (3.41) it follows that  . Since
. Since  was arbitrary we have that
was arbitrary we have that  , so
, so  . Thus, the pair
. Thus, the pair  is admissible for the evolution family
is admissible for the evolution family  .
.
Suppose that  is exponentially dichotomic with respect to the family of projections
is exponentially dichotomic with respect to the family of projections  and the constants
and the constants  . According to [13, Proposition 3.1] we have that
. According to [13, Proposition 3.1] we have that  , which implies that
, which implies that  , for all
, for all  . Then, we obtain that
. Then, we obtain that

or equivalently

which is absurd. In conclusion, the pair  is admissible for
is admissible for  , but, for all that, the evolution family
, but, for all that, the evolution family  is not exponentially dichotomic.
is not exponentially dichotomic.
4. Applications to the Case of 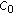 -Semigroups
-Semigroups
In this section, by applying the central theorems from the Section 3 we deduce several consequences of the main results for the study of exponential dichotomy of  -semigroups. Let
-semigroups. Let  be a real or complex Banach space.
be a real or complex Banach space.
Definition 4.1.
A family  of bounded linear operators on
of bounded linear operators on  is said to be a
is said to be a  -semigroup if the following properties are satisfied:
-semigroup if the following properties are satisfied:
-
(i)
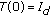 , the identity operator on
, the identity operator on 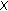 ;
; -
(ii)
 , for all
, for all 
-
(iii)
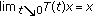 , for every
, for every 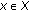 .
.
Definition 4.2.
A  -semigroup
-semigroup  is said to be exponentially dichotomic if there exist a projection
is said to be exponentially dichotomic if there exist a projection  and two constants
and two constants  and
and  such that
such that
-
(i)
 , for all
, for all 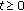 ;
; -
(ii)
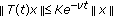 , for all
, for all 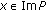 and all
and all 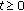 ;
; -
(iii)
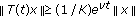 , for all
, for all 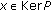 and all
and all  ;
; -
(iv)
the restriction
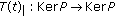 is an isomorphism, for every
is an isomorphism, for every 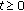 .
.
Remark 4.3.
-
(i)
If
 is a
is a  -semigroup, we can associate to
-semigroup, we can associate to 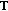 an evolution family
an evolution family 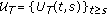 , by
, by  , for every
, for every 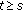 .
. -
(ii)
A
 -semigroup
-semigroup 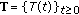 is exponentially dichotomic if and only if the associated evolution family
is exponentially dichotomic if and only if the associated evolution family 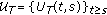 is exponentially dichotomic (see [12, Proposition 4.4]).
is exponentially dichotomic (see [12, Proposition 4.4]).
Let  be two Banach function spaces such that
be two Banach function spaces such that  and
and  .
.
Definition 4.4.
The pair  is said to be admissible for the
is said to be admissible for the  -semigroup
-semigroup  if for every
if for every  there is a unique
there is a unique  such that
such that

Theorem 4.5.
Let  be a
be a  -semigroup on the Banach space
-semigroup on the Banach space  and let
and let  be two Banach function spaces with
be two Banach function spaces with  and
and  . If
. If  or
or  , then the following assertions hold:
, then the following assertions hold:
-
(i)
if the pair
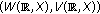 is admissible for
is admissible for 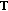 , then
, then 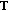 is uniformly exponentially dichotomic;
is uniformly exponentially dichotomic; -
(ii)
if
 and one of the spaces
and one of the spaces  belongs to the class
belongs to the class 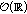 , then
, then 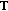 is exponentially dichotomic if and only if the pair
is exponentially dichotomic if and only if the pair  is admissible for
is admissible for 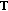 .
.
Proof.
This follows from Theorem 3.11 and Remark 4.3(ii).
Remark 4.6.
According to the example given in the previous section we deduce that the hypothesis  or
or  cannot be removed. Moreover, Theorem 4.5 provides a complete answer concerning the study of exponential dichotomy of semigroups using input-output techniques with respect to the associated integral equation.
cannot be removed. Moreover, Theorem 4.5 provides a complete answer concerning the study of exponential dichotomy of semigroups using input-output techniques with respect to the associated integral equation.
References
Daleckii JL, Krein MG: Stability of Solutions of Differential Equations in Banach Space, Translations of Mathematical Monographs. Volume 4. American Mathematical Society, Providence, RI, USA; 1974:vi+386.
Liu JH, N'Guérékata GM, Van Minh N: Topics on Stability and Periodicity in Abstract Differential Equations, Series on Concrete and Applicable Mathematics. Volume 6. World Scientific, Hackensack, NJ, USA; 2008:x+208.
Liu Q, Van Minh N, Nguerekata G, Yuan R: Massera type theorems for abstract functional differential equations. Funkcialaj Ekvacioj 2008,51(3):329-350. 10.1619/fesi.51.329
Massera JL, Schäffer JJ: Linear Differential Equations and Function Spaces, Pure and Applied Mathematics. Volume 21. Academic Press, New York, NY, USA; 1966:xx+404.
Van Minh N, Räbiger F, Schnaubelt R: Exponential stability, exponential expansiveness, and exponential dichotomy of evolution equations on the half-line. Integral Equations and Operator Theory 1998,32(3):332-353. 10.1007/BF01203774
Van Minh N, N'Guérékata GM, Yuan R: Lectures on the Asymptotic Behavior of Solutions of Differential Equations. Nova Science, New York, NY, USA; 2008:viii+65.
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences. Volume 44. Springer, New York, NY, USA; 1983:viii+279.
Perron O: Die Stabilitätsfrage bei Differentialgleichungen. Mathematische Zeitschrift 1930,32(1):703-728. 10.1007/BF01194662
Sasu B, Sasu AL:Exponential dichotomy and
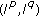 -admissibility on the half-line. Journal of Mathematical Analysis and Applications 2006,316(2):397-408. 10.1016/j.jmaa.2005.04.047
-admissibility on the half-line. Journal of Mathematical Analysis and Applications 2006,316(2):397-408. 10.1016/j.jmaa.2005.04.047Sasu B: Uniform dichotomy and exponential dichotomy of evolution families on the half-line. Journal of Mathematical Analysis and Applications 2006,323(2):1465-1478. 10.1016/j.jmaa.2005.12.002
Sasu AL, Sasu B: Exponential dichotomy on the real line and admissibility of function spaces. Integral Equations and Operator Theory 2006,54(1):113-130. 10.1007/s00020-004-1347-z
Sasu AL: Exponential dichotomy for evolution families on the real line. Abstract and Applied Analysis 2006, 2006:-6.
Sasu AL, Sasu B: Exponential dichotomy and admissibility for evolution families on the real line. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2006,13(1):1-26.
Sasu AL, Sasu B:Discrete admissibility,
 -spaces and exponential dichotomy on the real line. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2006,13(5):551-561.
-spaces and exponential dichotomy on the real line. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2006,13(5):551-561.Sasu B, Sasu AL:Exponential trichotomy and
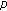 -admissibility for evolution families on the real line. Mathematische Zeitschrift 2006,253(3):515-536. 10.1007/s00209-005-0920-8
-admissibility for evolution families on the real line. Mathematische Zeitschrift 2006,253(3):515-536. 10.1007/s00209-005-0920-8Sasu AL: Integral equations on function spaces and dichotomy on the real line. Integral Equations and Operator Theory 2007,58(1):133-152. 10.1007/s00020-006-1478-5
Acknowledgment
This work is supported by the Exploratory Research Project PN 2 ID 1081 code 550/2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sasu, A.L. Pairs of Function Spaces and Exponential Dichotomy on the Real Line. Adv Differ Equ 2010, 347670 (2010). https://doi.org/10.1155/2010/347670
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/347670
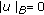 if and only if
if and only if  a.e.;
a.e.; , for all
, for all  ;
;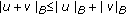 , for all
, for all 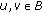 ;
; and
and 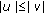 a.e. then
a.e. then 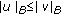 ;
; , then
, then 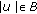 .
.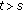 there is
there is 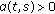 such that
such that  , for all
, for all  ;
;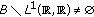 then there is a continuous function
then there is a continuous function 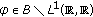 .
.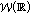 the class of all Banach function spaces
the class of all Banach function spaces 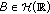 with
with 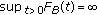 ;
;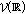 the class of all Banach function spaces
the class of all Banach function spaces  with the property that
with the property that 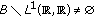 ;
;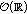 the class of all Banach function spaces
the class of all Banach function spaces 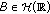 with the property that for every
with the property that for every  in
in 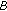 , the function
, the function  belongs to
belongs to  .
.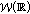 we refer to [
we refer to [ then there is a continuous function
then there is a continuous function  with
with 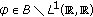 .
.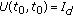 and
and 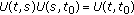 , for all
, for all 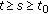 ;
;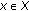 and every
and every 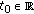 the mapping
the mapping 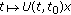 is continuous on
is continuous on 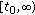 and the mapping
and the mapping  is continuous on
is continuous on 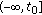 ;
; and
and  such that
such that 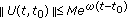 , for all
, for all  .
.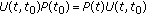 , for all
, for all 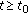 ;
;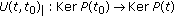 is an isomorphism, for all
is an isomorphism, for all  ;
;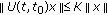 , for all
, for all 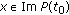 and all
and all  ;
;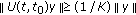 , for all
, for all  and all
and all 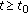 .
.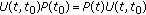 , for all
, for all 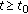 ;
;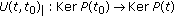 is an isomorphism, for all
is an isomorphism, for all 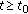 ;
;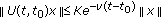 , for all
, for all 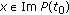 and all
and all 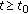 ;
;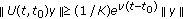 , for all
, for all  and all
and all 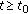 .
.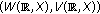 is admissible for
is admissible for 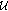 , then
, then 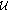 is uniformly exponentially dichotomic;
is uniformly exponentially dichotomic;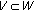 and one of the spaces
and one of the spaces 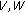 belongs to the class
belongs to the class 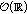 , then
, then 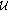 is exponentially dichotomic if and only if the pair
is exponentially dichotomic if and only if the pair 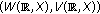 is admissible for
is admissible for  .
. is exponentially dichotomic with respect to the family of projections
is exponentially dichotomic with respect to the family of projections 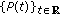 and the constants
and the constants 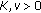 . Then, we have that
. Then, we have that 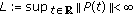 (see, e.g., [
(see, e.g., [ -Semigroups
-Semigroups , the identity operator on
, the identity operator on 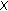 ;
; , for all
, for all 
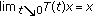 , for every
, for every 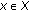 .
. , for all
, for all 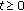 ;
;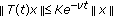 , for all
, for all 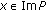 and all
and all 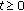 ;
;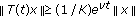 , for all
, for all 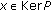 and all
and all  ;
;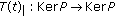 is an isomorphism, for every
is an isomorphism, for every 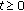 .
. is a
is a  -semigroup, we can associate to
-semigroup, we can associate to 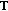 an evolution family
an evolution family 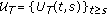 , by
, by  , for every
, for every 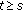 .
. -semigroup
-semigroup 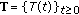 is exponentially dichotomic if and only if the associated evolution family
is exponentially dichotomic if and only if the associated evolution family 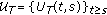 is exponentially dichotomic (see [
is exponentially dichotomic (see [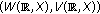 is admissible for
is admissible for 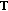 , then
, then 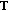 is uniformly exponentially dichotomic;
is uniformly exponentially dichotomic; and one of the spaces
and one of the spaces  belongs to the class
belongs to the class 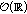 , then
, then 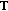 is exponentially dichotomic if and only if the pair
is exponentially dichotomic if and only if the pair  is admissible for
is admissible for 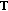 .
.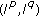 -admissibility on the half-line. Journal of Mathematical Analysis and Applications 2006,316(2):397-408. 10.1016/j.jmaa.2005.04.047
-admissibility on the half-line. Journal of Mathematical Analysis and Applications 2006,316(2):397-408. 10.1016/j.jmaa.2005.04.047 -spaces and exponential dichotomy on the real line. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2006,13(5):551-561.
-spaces and exponential dichotomy on the real line. Dynamics of Continuous, Discrete & Impulsive Systems. Series A 2006,13(5):551-561.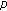 -admissibility for evolution families on the real line. Mathematische Zeitschrift 2006,253(3):515-536. 10.1007/s00209-005-0920-8
-admissibility for evolution families on the real line. Mathematische Zeitschrift 2006,253(3):515-536. 10.1007/s00209-005-0920-8