- Review Article
- Open access
- Published:
A Survey on Oscillation of Impulsive Ordinary Differential Equations
Advances in Difference Equations volume 2010, Article number: 354841 (2010)
Abstract
This paper summarizes a series of results on the oscillation of impulsive ordinary differential equations. We consider linear, half-linear, super-half-linear, and nonlinear equations. Several oscillation criteria are given. The Sturmian comparison theory for linear and half linear equations is also included.
1. Introduction
Impulsive differential equations, that is, differential equations involving impulse effect, appear as a natural description of observed evolution phenomena of several real world problems. There are many good monographs on the impulsive differential equations [1–6]. It is known that many biological phenomena, involving thresholds, bursting rhythm models in medicine and biology, optimal control models in economics, pharmacokinetics, and frequency modulates systems, do exhibit impulse effects. Let us describe the Kruger-Thiemer model [7] for drug distribution to show how impulses occur naturally. It is assumed that the drug, which is administered orally, is first dissolved into the gastrointestinal tract. The drug is then absorbed into the so-called apparent volume of distribution and finally eliminated from the system by the kidneys. Let  and
and  denote the amounts of drug at time
denote the amounts of drug at time  in the gastrointestinal tract and apparent volume of distribution, respectively, and let
in the gastrointestinal tract and apparent volume of distribution, respectively, and let  and
and  be the relevant rate constants. For simplicity, assume that
be the relevant rate constants. For simplicity, assume that  The dynamic description of this model is then given by
The dynamic description of this model is then given by

In [8], the authors postulate the following control problem. At discrete instants of time  , the drug is ingested in amounts
, the drug is ingested in amounts  This imposes the following boundary conditions:
This imposes the following boundary conditions:

To achieve the desired therapeutic effect, it is required that the amount of drug in the apparent volume of distribution never goes below a constant level or plateau  say, during the time interval
say, during the time interval  where
where  . Thus, we have the constraint
. Thus, we have the constraint

It is also assumed that only nonnegative amounts of the drug can be given. Then, a control vector is a point  in the nonnegative orthant of Euclidean space of dimension
in the nonnegative orthant of Euclidean space of dimension  . Hence,
. Hence,  . Finally, the biological cost function
. Finally, the biological cost function  minimizes both the side effects and the cost of the drug. The problem is to find
minimizes both the side effects and the cost of the drug. The problem is to find  subject to (1.1)–(1.3).
subject to (1.1)–(1.3).
The first investigation on the oscillation theory of impulsive differential equations was published in 1989 [9]. In that paper Gopalsamy and Zhang consider impulsive delay differential equations of the form


where  as
as  and
and  is a positive real number. Sufficient conditions are obtained for the asymptotic stability of the zero solution of (1.4) and existence of oscillatory solutions of (1.5). However, it seems that the problem of oscillation of ordinary differential equations with impulses has received attention much later [10]. Although, the theory of impulsive differential equations has been well established, the oscillation theory of such equations has developed rather slowly. To the best of our knowledge, except one paper [11], all of the investigations have been on differential equations subject to fixed moments of impulse effect. In [11], second-order differential equations with random impulses were dealt with, and there are no papers on the oscillation of differential equations with impulses at variable times.
is a positive real number. Sufficient conditions are obtained for the asymptotic stability of the zero solution of (1.4) and existence of oscillatory solutions of (1.5). However, it seems that the problem of oscillation of ordinary differential equations with impulses has received attention much later [10]. Although, the theory of impulsive differential equations has been well established, the oscillation theory of such equations has developed rather slowly. To the best of our knowledge, except one paper [11], all of the investigations have been on differential equations subject to fixed moments of impulse effect. In [11], second-order differential equations with random impulses were dealt with, and there are no papers on the oscillation of differential equations with impulses at variable times.
In this survey paper, our aim is to present the results (within our reach) obtained so far on the oscillation theory of impulsive ordinary differential equations. The paper is organized as follows. Section 2 includes notations, definitions, and some well-known oscillation theorems needed in later sections. In Section 3, we are concerned with linear impulsive differential equations. In Section 4, we deal with nonlinear impulsive differential equations.
2. Preliminaries
In this section, we introduce notations, definitions, and some well-known results which will be used in this survey paper.
Let  for some fixed
for some fixed  and
and  be a sequence in
be a sequence in  such that
such that  and
and 
By  we denote the set of all functions
we denote the set of all functions  which are continuous for
which are continuous for  and continuous from the left with discontinuities of the first kind at
and continuous from the left with discontinuities of the first kind at  Similarly,
Similarly,  is the set of functions
is the set of functions  having derivative
having derivative  . One has
. One has  ,
,  , or
, or  . In case
. In case  , we simply write
, we simply write  for
for  . As usual,
. As usual,  denotes the set of continuous functions from
denotes the set of continuous functions from  to
to  .
.
Consider the system of first-order impulsive ordinary differential equations having impulses at fixed moments of the form

where  ,
,  , and
, and

with  . The notation
. The notation  in place of
in place of  is also used. For simplicity, it is usually assumed that
is also used. For simplicity, it is usually assumed that  .
.
The qualitative theory of impulsive ordinary differential equations of the form (2.1) can be found in [1–6, 12].
Definition 2.1.
A function  is said to be a solution of (2.1) in an interval
is said to be a solution of (2.1) in an interval  if
if  satisfies (2.1) for
satisfies (2.1) for  .
.
For  , we may impose the initial condition
, we may impose the initial condition

Each solution  of (2.1) which is defined in the interval
of (2.1) which is defined in the interval  and satisfying the condition
and satisfying the condition  is said to be a solution of the initial value problem (2.1)-(2.3).
is said to be a solution of the initial value problem (2.1)-(2.3).
Note that if  then the solution of the initial value problem (2.1)-(2.3) coincides with the solution of
then the solution of the initial value problem (2.1)-(2.3) coincides with the solution of

on  .
.
Definition 2.2.
A real-valued function  , not necessarily a solution, is said to be oscillatory, if it is neither eventually positive nor eventually negative. Otherwise, it is called nonoscillatory. A differential equation is called oscillatory if all its solutions are oscillatory.
, not necessarily a solution, is said to be oscillatory, if it is neither eventually positive nor eventually negative. Otherwise, it is called nonoscillatory. A differential equation is called oscillatory if all its solutions are oscillatory.
For our purpose we now state some well-known results on oscillation of second-order ordinary differential equations without impulses.
Theorem 2.3 (see [13]).
Let  Then, the equation
Then, the equation

is oscillatory if

and nonoscillatory if

Theorem 2.4 (see [14]).
Let  and
and  be continuous functions and
be continuous functions and  . If
. If

then the equation

is oscillatory.
Theorem 2.5 (see [15]).
Let  be a positive and continuously differentiable function for
be a positive and continuously differentiable function for  and let
and let  If
If

then the equation

has nonoscillatory solutions, where  is an integer.
is an integer.
Theorem 2.6 (see [15]).
Let  be a positive and continuous function for
be a positive and continuous function for  and
and  an integer. Then every solution of (2.11) is oscillatory if and only if
an integer. Then every solution of (2.11) is oscillatory if and only if

3. Linear Equations
In this section, we consider the oscillation problem for first-, second-, and higher-order linear impulsive differential equations. Moreover, the Sturm type comparison theorems for second-order linear impulsive differential equations are included.
3.1. Oscillation of First-Order Linear Equations
Let us consider the linear impulsive differential equation

together with the corresponding inequalities:


The following theorems are proved in [1].
Theorem 3.1.
Let  and
and  Then the following assertions are equivalent.
Then the following assertions are equivalent.
-
(1)
The sequence
 has infinitely many negative terms.
has infinitely many negative terms. -
(2)
The inequality (3.2) has no eventually positive solution.
-
(3)
The inequality (3.3) has no eventually negative solution.
-
(4)
Each nonzero solution of (3.1) is oscillatory.
Proof.
(1) (2)
(2) Let the sequence
Let the sequence  have infinitely many negative terms. Let us suppose that the assertion (
have infinitely many negative terms. Let us suppose that the assertion ( ) is not true; that is, the inequality (3.2) has an eventually positive solution
) is not true; that is, the inequality (3.2) has an eventually positive solution  Let
Let  be such that
be such that  Then, it follows from (3.2) that
Then, it follows from (3.2) that

which is a contradiction.
(2) (3). The validity of this relation follows from the fact that if
(3). The validity of this relation follows from the fact that if  is a solution of the inequality (3.2), then
is a solution of the inequality (3.2), then  is a solution of the inequality (3.3) and vice versa.
is a solution of the inequality (3.3) and vice versa.
(2) and (3)  (4)
(4) In fact, if (3.1) has neither an eventually positive nor an eventually negative solution, then each nonzero solution of (3.1) is oscillatory.
In fact, if (3.1) has neither an eventually positive nor an eventually negative solution, then each nonzero solution of (3.1) is oscillatory.
(4) (1)
(1) If
If  is an oscillatory solution of (3.3), then it follows from the equality
is an oscillatory solution of (3.3), then it follows from the equality

that the sequence  has infinitely many negative terms.
has infinitely many negative terms.
The following theorem can be proved similarly.
Theorem 3.2.
Let  and
and  Then the following assertions are equivalent.
Then the following assertions are equivalent.
-
(1)
The sequence
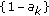 has finitely many negative terms.
has finitely many negative terms. -
(2)
The inequality (3.2) has an eventually positive solution.
-
(3)
The inequality (3.3) has an eventually negative solution.
-
(4)
Each nonzero solution of (3.1) is nonoscillatory.
It is known that (3.1) without impulses has no oscillatory solutions. But (3.1) (with impulses) can have oscillatory solutions. So, impulse actions determine the oscillatory properties of first-order linear differential equations.
3.2. Sturmian Theory for Second-Order Linear Equations
It is well-known that Sturm comparison theory plays an important role in the study of qualitative properties of the solutions of both linear and nonlinear equations. The first paper on the Sturm theory of impulsive differential equations was published in 1996. In [10], Bainov et al. derived a Sturmian type comparison theorem, a zeros-separation theorem, and a dichotomy theorem for second-order linear impulsive differential equations. Recently, the theory has been extended in various directions in [16–18], with emphasis on Picone's formulas, Wirtinger type inequalities, and Leighton type comparison theorems.
We begin with a series of results contained in [1, 10]. The second-order linear impulsive differential equations considered are


where  and
and  are continuous for
are continuous for  and they have a discontinuity of the first kind at the points
and they have a discontinuity of the first kind at the points  where they are continuous from the left.
where they are continuous from the left.
The main result is the following theorem, which is also valid for differential inequalities.
Suppose the following.
-
(1)
Equation (3.7) has a solution
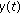 such that
such that 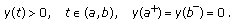 (3.8)
(3.8)
-
(2)
The following inequalities are valid:
 (3.9)
(3.9)
-
(3)
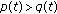 in a subinterval of
in a subinterval of 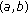 or
or 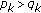 for some
for some 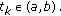
Then (3.6) has no positive solution  defined on
defined on 
Proof.
Assume that (3.6) has a solution  such that
such that  Then from the relation
Then from the relation

an integration yields

From (3.6), (3.7), condition ( ), and the above inequality, we conclude that
), and the above inequality, we conclude that

But, from conditions ( ) and (
) and ( ), it follows that the right side of the above inequality is negative, which leads to a contradiction. This completes the proof.
), it follows that the right side of the above inequality is negative, which leads to a contradiction. This completes the proof.
The following corollaries follow easily from Theorem 3.3.
Corollary 3.4 (Comparison Theorem).
Suppose the following.
-
(1)
Equation (3.7) has a solution
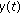 such that
such that  (3.13)
(3.13)
-
(2)
The following inequalities are valid:
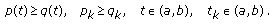 (3.14)
(3.14)
-
(3)
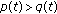 in some subinterval of
in some subinterval of 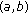 or
or 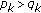 for some
for some 
Then, each solution  of (3.6) has at least one zero in
of (3.6) has at least one zero in 
Corollary 3.5.
If conditions ( 1) and ( 2) of Corollary 3.4 are satisfied, then one has the following.
-
(1)
Each solution
 of (3.6) for which
of (3.6) for which  has at least one zero in
has at least one zero in 
-
(2)
Each solution
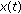 of (3.6) has at least one zero in
of (3.6) has at least one zero in 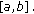
Corollary 3.6 (Oscillation Theorem).
Suppose the following.
-
(1)
There exists a solution
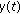 of (3.7) and a sequence of disjoint intervals
of (3.7) and a sequence of disjoint intervals 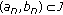 such that
such that 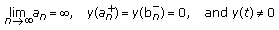 (3.15)
(3.15)
for 
-
(2)
The following inequalities are valid for
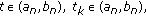 and
and  ;
; 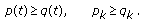 (3.16)
(3.16)
Then all solutions of (3.6) are oscillatory, and moreover, they change sign in each interval 
Corollary 3.7 (Comparison Theorem).
Let the inequalities  hold for
hold for  and
and  Then, all solutions of (3.7) are nonoscillatory if (3.6) has a nonoscillatory solution.
Then, all solutions of (3.7) are nonoscillatory if (3.6) has a nonoscillatory solution.
Corollary 3.8 (Separation Theorem).
The zeros of two linearly independent solutions of (3.6) separate one another; that is, the two solutions have no common zeros, and if  are two consecutive zeros of one of the solutions, then the interval
are two consecutive zeros of one of the solutions, then the interval  contains exactly one zero of the other solution.
contains exactly one zero of the other solution.
Corollary 3.9 (Dichotomy Theorem).
All solutions of (3.6) are oscillatory or nonoscillatory.
We can use Corollary 3.7, to deduce the following oscillation result for the equation:

Suppose the following.
-
(1)
The function
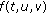 is such that if
is such that if  is a continuous function for
is a continuous function for  having a piecewise continuous derivative
having a piecewise continuous derivative  for
for  then the function
then the function  is piecewise continuous for
is piecewise continuous for 
-
(2)
The following inequalities are valid:
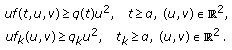 (3.18)
(3.18)
Then every solution  of (3.17) defined for
of (3.17) defined for  is oscillatory if (3.7) has an oscillatory solution.
is oscillatory if (3.7) has an oscillatory solution.
Recently, by establishing a Picone's formula and a Wirtinger type inequality, Özbekler and Zafer [17] have obtained similar results for second-order linear impulsive differential equations of the form


where  and
and  are real sequences,
are real sequences,  with
with  and
and  for all
for all 
Let  be a nondegenerate subinterval of
be a nondegenerate subinterval of  . In what follows we shall make use of the following condition:
. In what follows we shall make use of the following condition:

It is well-known that condition (H) is crucial in obtaining a Picone's formula in the case when impulses are absent. If (H) fails to hold, then Wirtinger, Leighton, and Sturm-Picone type results require employing a so-called "device of Picard." We will show how this is possible for impulsive differential equations as well.
Let (H) be satisfied. Suppose that  such that
such that  and
and  . These conditions simply mean that
. These conditions simply mean that  and
and  are in the domain of
are in the domain of  and
and  , respectively. If
, respectively. If  for any
for any  , then we may define
, then we may define

For clarity, we suppress the variable  . Clearly,
. Clearly,

In view of (3.19) and (3.20) it is not difficult to see from (3.22) that

Employing the identity

the following Picone's formula is easily obtained.
Theorem 3.11 (Picone's formula [17]).
Let (H) be satisfied. Suppose that  such that
such that  and
and  . If
. If  for any
for any  and
and  then
then

In a similar manner one may derive a Wirtinger type inequality.
Theorem 3.12 (Wirtinger type inequality [17]).
If there exists a solution  of (3.19) such that
of (3.19) such that  on
on  , then
, then

where

Corollary 3.13.
If there exists an  such that
such that  then every solution
then every solution  of (3.19) has a zero in
of (3.19) has a zero in  .
.
Corollary 3.14.
Suppose that for a given  there exists an interval
there exists an interval  and a function
and a function  for which
for which  . Then (3.19) is oscillatory.
. Then (3.19) is oscillatory.
Next, we give a Leighton type comparison theorem.
Theorem 3.15 (Leighton type comparison [17]).
Suppose that there exists a solution  of (3.19). If (H) is satisfied with
of (3.19). If (H) is satisfied with  and
and

then every solution  of (3.20) must have at least one zero in
of (3.20) must have at least one zero in  .
.
Proof.
Let  and
and  . Since
. Since  and
and  are solutions of (3.19) and (3.20), respectively, we have
are solutions of (3.19) and (3.20), respectively, we have  . Employing Picone's formula (3.25), we see that
. Employing Picone's formula (3.25), we see that

The functions under integral sign are all integrable, and regardless of the values of  or
or  , the left-hand side of (3.29) tends to zero as
, the left-hand side of (3.29) tends to zero as  . Clearly, (3.29) results in
. Clearly, (3.29) results in

which contradicts (3.28).
Corollary 3.16 (Sturm-Picone type comparison).
Let  be a solution of (3.19) having two consecutive zeros
be a solution of (3.19) having two consecutive zeros  . Suppose that (H) holds, and
. Suppose that (H) holds, and


for all  , and
, and

for all  for which
for which  .
.
If either (3.31) or (3.32) is strict in a subinterval of  or (3.33) is strict for some
or (3.33) is strict for some  , then every solution
, then every solution  of (3.20) must have at least one zero on
of (3.20) must have at least one zero on  .
.
Corollary 3.17.
Suppose that conditions (3.31)-(3.32) are satisfied for all  for some integer
for some integer  , and that (3.33) is satisfied for all
, and that (3.33) is satisfied for all  for which
for which  . If one of the inequalities (3.31)–(3.33) is strict, then (3.20) is oscillatory whenever any solution
. If one of the inequalities (3.31)–(3.33) is strict, then (3.20) is oscillatory whenever any solution  of (3.19) is oscillatory.
of (3.19) is oscillatory.
As a consequence of Theorem 3.15 and Corollary 3.16, we have the following oscillation result.
Corollary 3.18.
Suppose for a given  there exists an interval
there exists an interval  for which that condition of either Theorem 3.15 or Corollary 3.16 are satisfied. Then (3.20) is oscillatory.
for which that condition of either Theorem 3.15 or Corollary 3.16 are satisfied. Then (3.20) is oscillatory.
If (H) does not hold, we introduce a setting, which is based on a device of Picard, leading to different versions of Corollary 3.16.
Indeed, for any  we have
we have

Let

It follows that

Assuming that  , the choice of
, the choice of  yields
yields

Then, we have the following result.
Theorem 3.19 (Device of Picard [17]).
Let  and let
and let  be a solution of (3.19) having two consecutive zeros
be a solution of (3.19) having two consecutive zeros  and
and  in
in  . Suppose that
. Suppose that


are satisfied for all  , and that
, and that

for all  for which
for which  .
.
If either (3.38) or (3.39) is strict in a subinterval of  or (3.40) is strict for some
or (3.40) is strict for some  , then any solution
, then any solution  of (3.20) must have at least one zero in
of (3.20) must have at least one zero in  .
.
Corollary 3.20.
Suppose that (3.38)-(3.39) are satisfied for all  for some integer
for some integer  , and that (3.40) is satisfied for all
, and that (3.40) is satisfied for all  for which
for which  . If
. If  and one of the inequalities (3.38)–(3.40) is strict, then (3.20) is oscillatory whenever any solution
and one of the inequalities (3.38)–(3.40) is strict, then (3.20) is oscillatory whenever any solution  of (3.19) is oscillatory.
of (3.19) is oscillatory.
As a consequence of Theorem 3.19, we have the following Leighton type comparison result which is analogous to Theorem 3.15.
Theorem 3.21 (Leighton type comparison [17]).
Let  . If there exists a solution
. If there exists a solution  of (3.19) such that
of (3.19) such that

then every solution  of (3.20) must have at least one zero in
of (3.20) must have at least one zero in  .
.
As a consequence of Theorems 3.19 and 3.21, we have the following oscillation result.
Corollary 3.22.
Suppose that for a given  there exists an interval
there exists an interval  for which conditions of either Theorem 3.19 or Theorem 3.21 are satisfied. Then (3.20) is oscillatory.
for which conditions of either Theorem 3.19 or Theorem 3.21 are satisfied. Then (3.20) is oscillatory.
Moreover, it is possible to obtain results for (3.20) analogous to Theorem 3.12 and Corollary 3.13.
Theorem 3.23 (Wirtinger type inequality [17]).
If there exists a solution  of (3.20) such that
of (3.20) such that  on
on  , then for
, then for  and for all
and for all 

Corollary 3.24.
If there exists an  with
with  such that
such that  then every solution
then every solution  of (3.20) must have at least one zero in
of (3.20) must have at least one zero in  .
.
As an immediate consequence of Corollary 3.24, we have the following oscillation result.
Corollary 3.25.
Suppose that for a given  there exists an interval
there exists an interval  and a function
and a function  with
with  for which
for which  . Then (3.20) is oscillatory.
. Then (3.20) is oscillatory.
3.3. Oscillation of Second-Order Linear Equations
The oscillation theory of second-order impulsive differential equations has developed rapidly in the last decade. For linear equations, we refer to the papers [11, 19–21].
Let us consider the second-order linear differential equation with impulses

where  ,
,  and
and  are two known sequences of real numbers, and
are two known sequences of real numbers, and

For (3.43), it is clear that if  for all large
for all large  then (3.43) is oscillatory. So, we assume that
then (3.43) is oscillatory. So, we assume that  The following theorem gives the relation between the existence of oscillatory solutions of (3.43) and the existence of oscillatory solutions of second-order linear nonimpulsive differential equation:
The following theorem gives the relation between the existence of oscillatory solutions of (3.43) and the existence of oscillatory solutions of second-order linear nonimpulsive differential equation:

Theorem 3.26 (see [19]).
Assume that  Then the oscillation of all solutions of (3.43) is equivalent to the oscillation of all solutions of (3.45).
Then the oscillation of all solutions of (3.43) is equivalent to the oscillation of all solutions of (3.45).
Proof.
Let  be any solution of (3.43). Set
be any solution of (3.43). Set  for
for  Then, for all
Then, for all  we have
we have

Thus,  is continuous on
is continuous on  Furthermore, for
Furthermore, for  we have
we have

For  it can be shown that
it can be shown that

Thus,  is continuous if we define the value of
is continuous if we define the value of  at
at  as
as

Now, we have for 

and for 

Thus, we obtain

This shows that  is the solution of (3.45).
is the solution of (3.45).
Conversely, if  is the continuous solution of (3.45), we set
is the continuous solution of (3.45), we set  for
for  Then,
Then,  and
and  Furthermore, for
Furthermore, for  we have
we have

and so

Thus,  is the solution of (3.43). This completes the proof.
is the solution of (3.43). This completes the proof.
By Theorems 3.26 and 2.3, one may easily get the following corollary.
Corollary 3.27.
Assume that  . Then, (3.43) is oscillatory if
. Then, (3.43) is oscillatory if

and nonoscillatory if

When  and
and  oscillation criteria for (3.43) can be obtained by means of a Riccati technique as well. First, we need the following lemma.
oscillation criteria for (3.43) can be obtained by means of a Riccati technique as well. First, we need the following lemma.
Lemma 3.28.
Assume that  on any interval
on any interval  and let
and let  be an eventually positive solution of (3.43). If
be an eventually positive solution of (3.43). If

where  then, eventually
then, eventually 
Now, let  be an eventually positive solution of (3.43) such that
be an eventually positive solution of (3.43) such that  and
and  for
for  Under conditions of Lemma 3.28, let
Under conditions of Lemma 3.28, let  for
for  Then, (3.43) leads to an impulsive Riccati equation:
Then, (3.43) leads to an impulsive Riccati equation:

where 
Theorem 3.29 (see [19]).
Equation (3.43) is oscillatory if the second-order self-adjoint differential equation

is oscillatory, where 
Proof.
Assume, for the sake of contradiction, that (3.43) has a nonoscillatory solution  such that
such that  for
for  Now, define
Now, define

Then, it can be shown that  is continuous and satisfies
is continuous and satisfies

Next, we define

Then  is a solution of (3.59). This completes the proof.
is a solution of (3.59). This completes the proof.
By Theorems 3.29 and 2.4, we have the following corollary.
Corollary 3.30.
Assume that

where  Then, (3.43) is oscillatory.
Then, (3.43) is oscillatory.
Example 3.31 (see [19]).
Consider the equation

If  for some integer
for some integer  then it is easy to see that
then it is easy to see that

where  denotes the greatest integer function, and
denotes the greatest integer function, and

Thus, by Corollary 3.30, (3.64) is oscillatory. We note that the corresponding differential equation without impulses

is nonoscillatory by Theorem 2.3.
In [20], Luo and Shen used the above method to discuss the oscillation and nonoscillation of the second-order differential equation:

where 
In [21], the oscillatory and nonoscillatory properties of the second-order linear impulsive differential equation

is investigated, where

 for all
for all  and
and  is the
is the  -function, that is,
-function, that is,

for all  being continuous at
being continuous at  Before giving the main result, we need the following lemmas. For each
Before giving the main result, we need the following lemmas. For each  define the sequence
define the sequence  inductively by
inductively by

where  provided
provided  and
and  provided
provided  Let
Let 
Lemma 3.32.
If  for some
for some  then
then  and
and  for all
for all 
Proof.
By induction and in view of the fact that the function  is increasing in
is increasing in  it can be seen that
it can be seen that

Hence, 
The next lemma can also be proved by induction.
Lemma 3.33.
Suppose that  and
and  for all
for all  Define, by induction,
Define, by induction,

If  for all
for all  then
then

The following theorem is the main result of [21]. The proof uses the above two lemmas and the induction principle.
Theorem 3.34.
The following statements are equivalent.
-
(i)
There is
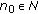 such that
such that 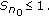
-
(ii)
There is
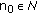 such that
such that 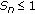 for all
for all 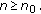
-
(iii)
Equation (3.69) is nonoscillatory.
-
(iv)
Equation (3.69) has a nonoscillatory solution.
Applying Theorem 3.34, the nonoscillation and oscillation of (3.69), in the case of  and
and  are investigated in [21].
are investigated in [21].
In all the publications mentioned above, the authors have considered differential equations with fixed moments of impulse actions. That is, it is assumed that the jumps happen at fixed points. However, jumps can be at random points as well. The oscillation of impulsive differential equations with random impulses was investigated in [11]. Below we give the results obtained in this case.
Let  be a random variable defined in
be a random variable defined in  and let
and let  be a constant. Consider the second-order linear differential equation with random impulses:
be a constant. Consider the second-order linear differential equation with random impulses:

where  are Lebesque measurable and locally essentially bounded functions,
are Lebesque measurable and locally essentially bounded functions,  ,
,  for all
for all  and
and 
Definition 3.35.
Let  be a real-valued random variable in the probability space
be a real-valued random variable in the probability space  where
where  is the sample space,
is the sample space,  is the
is the  -field, and
-field, and  is the probability measure. If
is the probability measure. If  , then
, then  is called the expectation of
is called the expectation of and is denoted by
and is denoted by  that is,
that is,

In particular, if  is a continuous random variable having probability density function
is a continuous random variable having probability density function  then
then

Definition 3.36.
A stochastic process  is said to be a sample path solution to(3.76) with the initial condition
is said to be a sample path solution to(3.76) with the initial condition  if for any sample value
if for any sample value  of
of  then
then  satisfies
satisfies

Definition 3.37.
The exponential distribution is a continuous random variable with the probability density function:

where  is a parameter.
is a parameter.
Definition 3.38.
A solution  of (3.76) is said to be nonoscillatory in mean if
of (3.76) is said to be nonoscillatory in mean if  is either eventually positive or eventually negative. Otherwise, it is called oscillatory.
is either eventually positive or eventually negative. Otherwise, it is called oscillatory.
Consider the following auxiliary differential equation:

Lemma 3.39.
The function  is a solution of (3.76) if and only if
is a solution of (3.76) if and only if

where  is a solution of (3.81) with the same initial conditions for (3.76), and
is a solution of (3.81) with the same initial conditions for (3.76), and  is the index function, that is,
is the index function, that is,

Proof.
If  is a solution of system (3.81), for any
is a solution of system (3.81), for any  we have
we have

It can be seen that

which imply that  satisfies (3.76), that is,
satisfies (3.76), that is,  is a sample path solution of (3.76). If
is a sample path solution of (3.76). If  is a sample path solution of (3.76), then it is easy to check that
is a sample path solution of (3.76), then it is easy to check that  is a solution of (3.81). This completes the proof.
is a solution of (3.81). This completes the proof.
Theorem 3.40 (see [11]).
Let the following condition hold.
(C) Let  be exponential distribution with parameter
be exponential distribution with parameter  ,
,  and let
and let  be independent of
be independent of  if
if 
If there exists  such that
such that

does not change sign for all  then all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory.
then all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory.
Proof.
Let  be any sample path solution of (3.76); then Lemma 3.39 implies
be any sample path solution of (3.76); then Lemma 3.39 implies

where  is a solution of (3.81). Hence,
is a solution of (3.81). Hence,

Further, it can be seen that

So,

By assumption,  has the same sign as
has the same sign as  for all
for all  That is, all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory. This completes the proof.
That is, all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory. This completes the proof.
When  is finite,
is finite,  , then the following result can be proved.
, then the following result can be proved.
Theorem 3.41 (see [11]).
Let condition (C) hold, and let  be finite for all
be finite for all  . Further assume that there are a finite number of
. Further assume that there are a finite number of  such that
such that  Then all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory.
Then all solutions of (3.76) are oscillatory in mean if and only if all solutions of (3.81) are oscillatory.
3.4. Oscillation of Higher-Order Linear Equations
Unlike the second-order impulsive differential equations, there are only very few papers on the oscillation of higher-order linear impulsive differential equations. Below we provide some results for third-order equations given in [22]. For higher-order liner impulsive differential equations we refer to the papers [23, 24].
Let us consider the third-order linear impulsive differential equation of the form

where  and
and  is not always zero in
is not always zero in  for sufficiently large
for sufficiently large 
The following lemma is a generalization of Lemma  in [25].
in [25].
Lemma 3.42 (see [22]).
Assume that  is a solution of (3.91) and there exists
is a solution of (3.91) and there exists  such that for any
such that for any  Let the following conditions be fulfilled.
Let the following conditions be fulfilled.
One has

One has

Then for sufficiently large  either
either  or
or  holds, where
holds, where
(A) one has

(B) one has

Theorem 3.43 (see [22]).
Assume that conditions of Lemma 3.42 are fulfilled and for any 
 and
and  Moreover, assume that the sequence of numbers
Moreover, assume that the sequence of numbers  has a positive lower bound,
has a positive lower bound,  converges, and
converges, and  holds. Then every bounded solution of (3.91) either oscillates or tends asymptotically to zero with fixed sign.
holds. Then every bounded solution of (3.91) either oscillates or tends asymptotically to zero with fixed sign.
Proof.
Suppose that  is a bounded nonoscillatory solution of (3.91) and
is a bounded nonoscillatory solution of (3.91) and  According to Lemma 3.42, either
According to Lemma 3.42, either  or
or  is satisfied. We claim that
is satisfied. We claim that  does not hold. Otherwise,
does not hold. Otherwise,  for some
for some  Since
Since  it follows that
it follows that  is monotonically increasing for
is monotonically increasing for  For any
For any  ,
,  By induction, it can be seen that
By induction, it can be seen that

in particular,

Integrating  from
from  to
to  we obtain
we obtain

By induction, for any natural number  we have
we have

Considering the condition  in Lemma 3.42 and the sequence of numbers
in Lemma 3.42 and the sequence of numbers  has a positive lower bound, we conclude that the inequality above leads to a contradiction that the right side tends to
has a positive lower bound, we conclude that the inequality above leads to a contradiction that the right side tends to  while
while  is bounded. Therefore, case
is bounded. Therefore, case  holds.
holds.  implies that
implies that  is strictly monotonically decreasing. From the facts that the series
is strictly monotonically decreasing. From the facts that the series  converges and
converges and  is bounded, it follows that
is bounded, it follows that  converges and there exists limit
converges and there exists limit  where
where  Now, we claim that
Now, we claim that  Otherwise,
Otherwise,  and there exists
and there exists  such that
such that  for
for  From (3.91) and the last inequality, we can deduce
From (3.91) and the last inequality, we can deduce

Integrating by parts of the above inequality and considering  and
and  , we have the following inequality:
, we have the following inequality:

Since  and the series
and the series  converges, the above inequality contradicts the fact that
converges, the above inequality contradicts the fact that  is bounded, hence
is bounded, hence  , and the proof is complete.
, and the proof is complete.
The proof of the following theorem is similar.
Theorem 3.44 (see [22]).
Assume that conditions of Lemma 3.42 hold and for any  , and
, and  Moreover, assume that the sequence of numbers
Moreover, assume that the sequence of numbers  is bounded above,
is bounded above,  converges, and
converges, and  holds. Then every solution of (3.91) either oscillates or tends asymptotically to zero with fixed sign.
holds. Then every solution of (3.91) either oscillates or tends asymptotically to zero with fixed sign.
Some results similar to the above theorems have been obtained for fourth-order linear impulsive differential equations; see [24].
4. Nonlinear Equations
In this section we present several oscillation theorems known for super-liner, half-linear, super-half-linear, and fully nonlinear impulsive differential equations of second and higher-orders. We begin with Sturmian and Leighton type comparison theorems for half-linear equations.
4.1. Sturmian Theory for Half-Linear Equations
Consider the second-order half linear impulsive differential equations of the form:


where  and
and  are real sequences, and
are real sequences, and  with
with  and
and 
The lemma below can be found in [26].
Lemma 4.1.
Let  and
and  be a constant; then
be a constant; then

where equality holds if and only if  .
.
The results of this section are from [16].
Theorem 4.2 (Sturm-Picone type comparison).
Let  be a solution of (4.1) having two consecutive zeros
be a solution of (4.1) having two consecutive zeros  and
and  in
in  . Suppose that
. Suppose that  and
and  are satisfied for all
are satisfied for all  , and that
, and that  for all
for all  for which
for which  . If either
. If either  or
or  or
or  , then any solution
, then any solution  of (4.2) must have at least one zero in
of (4.2) must have at least one zero in  .
.
Proof.
Assume that  never vanishes on
never vanishes on  . Define
. Define

where the dependence on  of the solutions
of the solutions  and
and  is suppressed. It is not difficult to see that
is suppressed. It is not difficult to see that


Clearly, the last term of (4.5) is integrable over  if
if  and
and  . Moreover,
. Moreover,  in this case. Suppose that
in this case. Suppose that  . The case
. The case  is similar. Since
is similar. Since  and
and

we get

and so

Moreover,

Integrating (4.5) from  to
to  and using (4.6), we see that
and using (4.6), we see that

where we have used Lemma 4.1 with  ,
,  , and
, and  . It is clear that (4.11) is not possible under our assumptions, and hence
. It is clear that (4.11) is not possible under our assumptions, and hence  must have a zero in
must have a zero in  .
.
Corollary 4.3 (Separation Theorem).
The zeros of two linearly independent solutions  and
and  of (4.1) separate each other.
of (4.1) separate each other.
Corollary 4.4 (Comparison Theorem).
Suppose that  and
and  are satisfied for all
are satisfied for all  for some
for some  , and that
, and that  for all
for all  for which
for which  . If either
. If either  or
or  or
or  , then every solution
, then every solution  of (4.2) is oscillatory whenever a solution
of (4.2) is oscillatory whenever a solution  of (4.1) is oscillatory.
of (4.1) is oscillatory.
Corollary 4.5 (Dichotomy Theorem).
The solutions of (4.1) are either all oscillatory or all nonoscillatory.
Theorem 4.6 (Leighton-type Comparison).
Let  be a solution of (4.1) having two consecutive zeros
be a solution of (4.1) having two consecutive zeros  and
and  in
in  . Suppose that
. Suppose that

Then any nontrivial solution  of (4.2) must have at least one zero in
of (4.2) must have at least one zero in  .
.
Proof.
Assume that  has no zero in
has no zero in  . Define the function
. Define the function  as in (4.4).
as in (4.4).
Clearly, (4.5) and (4.6) hold. It follows that

which is a contradiction. Therefore,  must have a zero on
must have a zero on  .
.
If  , then we may conclude that either
, then we may conclude that either  has a zero in
has a zero in  or
or  is a constant multiple of
is a constant multiple of  .
.
As a consequence of Theorems 4.2 and 4.6, we have the following oscillation result.
Corollary 4.7.
Suppose for a given  there exists an interval
there exists an interval  for which either conditions of Theorem 4.2 or Theorem 4.6 are satisfied, then every solution
for which either conditions of Theorem 4.2 or Theorem 4.6 are satisfied, then every solution  of (4.2) is oscillatory.
of (4.2) is oscillatory.
4.2. Oscillation of Second-Order Superlinear and Super-Half-Linear Equations
Let us consider the forced superlinear second-order differential equation of the following form:

where  denotes the impulse moments sequence with
denotes the impulse moments sequence with 

Assume that the following conditions hold.
()  is a constant,
is a constant,  is a continuous function,
is a continuous function,  .
.
()  are constants,
are constants, 
()  and
and  are two intervals such that
are two intervals such that  with
with  for
for  and
and  for
for 
 for
for 
Interval oscillation criteria for (4.14) are given in [27]. Denote  and for
and for  let
let 

Theorem 4.8 (see [27]).
Assume that conditions (A1)–(A3) hold, and that there exists  such that
such that

where  for
for  and
and

for  Then every solution of (4.14) has at least one zero in
Then every solution of (4.14) has at least one zero in 
Proof.
Let  be a solution of (4.14). Suppose that
be a solution of (4.14). Suppose that  does not have any zero in
does not have any zero in  Without loss of generality, we may assume that
Without loss of generality, we may assume that  for
for  Define
Define

Then, by Hölder's inequality, for  and
and  we have
we have

For  we obtain
we obtain

If  then all impulsive moments are in
then all impulsive moments are in  Multiplying both sides of (4.19) by
Multiplying both sides of (4.19) by  and integrating on
and integrating on  and using the hypotheses, we get
and using the hypotheses, we get

On the other hand, for  it follows that
it follows that

which implies that  is nonincreasing on
is nonincreasing on  So, for any
So, for any  one has
one has

It follows from the above inequality that

Making a similar analysis on  we obtain
we obtain

From (4.21)–(4.25) and  we get
we get

which contradicts (4.16). If  then
then  and there are no impulse moments in
and there are no impulse moments in  Similarly to the proof of (4.21), we get
Similarly to the proof of (4.21), we get

which again contradicts (4.16).
In the case  one can repeat the above procedure on the subinterval
one can repeat the above procedure on the subinterval  in place of
in place of  This completes the proof.
This completes the proof.
Corollary 4.9.
Assume that conditions (A1) and (A2) hold. If for any  there exist
there exist  satisfying (A3) with
satisfying (A3) with  and
and  satisfying (4.16),
satisfying (4.16),  then (4.14) is oscillatory.
then (4.14) is oscillatory.
The proof of following theorem is similar to that of Theorem 4.8.
Theorem 4.10 (see [27]).
Assume that conditions (A1)–(A3) hold, and there exists a  such that
such that

where  for
for  and
and

for  Then every solution of (4.14) has at least one zero in
Then every solution of (4.14) has at least one zero in 
Corollary 4.11.
Assume that conditions (A1) and (A2) hold. If for any  there exist
there exist  satisfying (A3) with
satisfying (A3) with  and
and  satisfying (4.28),
satisfying (4.28),  then (4.14) is oscillatory.
then (4.14) is oscillatory.
Example 4.12.
Consider the following superlinear impulsive differential equation:

It can be seen that if

then, conditions of Corollary 4.9 are satisfied; here  is the gamma function, and
is the gamma function, and  and
and  satisfy (
satisfy ( 2). So, every solution of (4.30) is oscillatory.
2). So, every solution of (4.30) is oscillatory.
In [28–30], the authors have used an energy function approach to obtain conditions for the existence of oscillatory or nonoscillatory solutions of the half-linear impulsive differential equations of the following form:

where  for
for 
Define the energy functional

where in explicit form  and
and  The functions
The functions  and
and  are both even and positive definite.
are both even and positive definite.
The function  is constant along the solutions of the nonimpulsive equation
is constant along the solutions of the nonimpulsive equation

The change in the energy along the solutions of (4.32) is given by

We see that these impulsive perturbations increase the energy. If the energy increases slowly, then we expect the solutions to oscillate. On the other hand, if the energy increases too fast, the solutions become nonoscillatory. Let  be a solution of (4.32),
be a solution of (4.32),  and
and  Calculating
Calculating  in terms of
in terms of  we obtain
we obtain

To simplify the notation, we introduce the function

The function  gives the jump in the quantity
gives the jump in the quantity  Note that
Note that  for
for  and
and  is monotone increasing with respect to
is monotone increasing with respect to  and decreasing with respect to
and decreasing with respect to 
Theorem 4.13 (see [29]).
Assume that there exist a constant  and a sequence
and a sequence  with
with  such that
such that

holds for every  Then every solution of (4.32) is nonoscillatory.
Then every solution of (4.32) is nonoscillatory.
Theorem 4.14 (see [29]).
Assume that there exist a constant  and a sequence
and a sequence  with
with  and
and  such that for every
such that for every 

holds for every  Then every solution of (4.32) is oscillatory.
Then every solution of (4.32) is oscillatory.
Proof.
Let  be a nontrivial solution of (4.32). It suffices to show that
be a nontrivial solution of (4.32). It suffices to show that  cannot hold on any interval
cannot hold on any interval  Assume that to the contrary,
Assume that to the contrary,  for
for  Let
Let  be defined by
be defined by  where
where  It follows from (4.39) that
It follows from (4.39) that  Hence,
Hence,

Since  and the right side of the above inequality tends to infinity as
and the right side of the above inequality tends to infinity as  we have a contradiction.
we have a contradiction.
Now, assume that  for every
for every  It can be shown that the integral
It can be shown that the integral

takes its maximum in  at
at

In the special case  we have the following necessary and sufficient condition.
we have the following necessary and sufficient condition.
Theorem 4.15 (see [29]).
Assume that  Then every solution of (4.32) is nonoscillatory if and only if
Then every solution of (4.32) is nonoscillatory if and only if

Remark 4.16.
Equation (4.32) with  was studied in [30].
was studied in [30].
Finally, we consider the second-order impulsive differential equation of the following form:

where  ,
,  are real constants,
are real constants,  is a strictly increasing unbounded sequence of real numbers,
is a strictly increasing unbounded sequence of real numbers,  and
and  are real sequences,
are real sequences,  , and
, and 
All results given in the remainder of this section are from [31].
Theorem 4.17.
Suppose that for any given  , there exist intervals
, there exist intervals  ,
,  , such that
, such that
-
(a)
 for all
for all  and
and 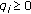 for all
for all 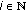 for which
for which  ;
; -
(b)
 ,
,  ,
,  ,
, 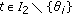 ;
;  ,
, 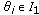 ,
,  ,
,  for all
for all 
If there exists  such that
such that

where


then (4.44) is oscillatory.
Proof.
Suppose that there exists a nonoscillatory solution  of (4.44) so that
of (4.44) so that  for all
for all  for some
for some  . Let
. Let

It follows that for  ,
,

where  dependence is suppressed for clarity.
dependence is suppressed for clarity.
Define a function  by
by

It is not difficult to see that if  , then
, then

Clearly, if  , then we have
, then we have  . Thus, with our convention that
. Thus, with our convention that  , (4.51) holds for
, (4.51) holds for  .
.
Suppose that  for all
for all  . Choose
. Choose  and consider the interval
and consider the interval  . From (b), we see that
. From (b), we see that  on
on  and
and  for all
for all  for which
for which  . Applying (4.51) to the terms in the parenthesis in (4.49) we obtain
. Applying (4.51) to the terms in the parenthesis in (4.49) we obtain

where  and
and  are defined by (4.46) and (4.47), respectively.
are defined by (4.46) and (4.47), respectively.
Let  . Multiplying (4.52) by
. Multiplying (4.52) by  and integrating over
and integrating over  give
give

In view of (4.52) and the assumption  , employing the integration by parts formula in the last integral we have
, employing the integration by parts formula in the last integral we have

We use Lemma 4.1 with

to obtain

which obviously contradicts (4.45).
If  is eventually negative then we can consider
is eventually negative then we can consider  and reach a similar contradiction. This completes the proof.
and reach a similar contradiction. This completes the proof.
Example 4.18.
Consider

where  is a positive real number.
is a positive real number.
Let  ,
,  , and
, and  . For any given
. For any given  we may choose
we may choose  sufficiently large so that
sufficiently large so that  . Then conditions (a)-(b) are satisfied. It is also easy to see that, for
. Then conditions (a)-(b) are satisfied. It is also easy to see that, for  and
and  ,
,

where  and
and  . It follows from Theorem 4.17 that (4.57) is oscillatory if
. It follows from Theorem 4.17 that (4.57) is oscillatory if

Note that if there is no impulse then the above integrals are negative, and therefore no conclusion can be drawn.
When  , then (4.44) reduces to forced half-linear impulsive equation with damping
, then (4.44) reduces to forced half-linear impulsive equation with damping

Corollary 4.19.
Suppose that for any given  , there exist intervals
, there exist intervals  ,
,  for which (a)-(b) hold.
for which (a)-(b) hold.
If there exists  such that
such that

then (4.60) is oscillatory.
Taking  in (4.44), we have the forced superlinear impulsive equation with damping
in (4.44), we have the forced superlinear impulsive equation with damping

Corollary 4.20.
Let  . Suppose that for any given
. Suppose that for any given  , there exist intervals
, there exist intervals  ,
,  , such that (a)-(b) hold for all
, such that (a)-(b) hold for all  .
.
If there exists  such that
such that

then (4.62) is oscillatory.
Let  in (4.62). Then we have the forced linear equation:
in (4.62). Then we have the forced linear equation:

Corollary 4.21.
Suppose that for any given  , there exist intervals
, there exist intervals  ,
,  , such that (a)-(b) hold for all
, such that (a)-(b) hold for all  .
.
If there exists  such that
such that

then (4.64) is oscillatory.
Example 4.22.
Consider

where  is a positive real number.
is a positive real number.
Let  . For any
. For any  , choose
, choose  sufficiently large so that
sufficiently large so that  and set
and set  and
and  . Clearly, (a)-(b) are satisfied for all
. Clearly, (a)-(b) are satisfied for all  . It is easy to see that for
. It is easy to see that for  and
and  ,
,

Thus (4.65) holds if

which by Corollary 4.21 is sufficient for oscillation of (4.66).
Note that if the impulses are removed, then (4.66) becomes nonoscillatory with a nonoscillatory solution  .
.
Finally we state a generalization of Theorem 4.17 for a class of more general type impulsive equations. Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be as above, and consider
be as above, and consider

where the functions  and
and  satisfy
satisfy

Theorem 4.23.
In addition to conditions of Theorem 4.17, if (4.70) holds then (4.69) is oscillatory.
Example 4.24.
Consider

where

Clearly if we take  and
and  , then (4.70) holds with
, then (4.70) holds with  ,
,  and
and  . Further, we see that all conditions of Theorem 4.17 are satisfied if
. Further, we see that all conditions of Theorem 4.17 are satisfied if  and
and  ; see Example 4.18. Therefore we may deduce from Theorem 4.23 that (4.71) is oscillatory if
; see Example 4.18. Therefore we may deduce from Theorem 4.23 that (4.71) is oscillatory if  .
.
4.3. Oscillation of Second-Order Nonlinear Equations
In this section, we first consider the second-order nonlinear impulsive differential equations of the following form:

Assume that the following conditions hold.
-
(i)
 and
and  where
where  ,
, 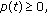 and
and 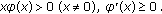
-
(ii)
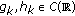 , and there exist positive numbers
, and there exist positive numbers 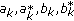 such that
such that 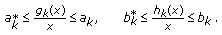 (4.74)
(4.74)
In most of the investigations about oscillation of nonlinear impulsive differential equations, the following lemma is an important tool.
Lemma 4.25 (see [25]).
Let  be a solution of (4.73). Suppose that there exists some
be a solution of (4.73). Suppose that there exists some  such that
such that  for
for  If conditions (i) and (ii) are satisfied, and
If conditions (i) and (ii) are satisfied, and
(iii)

 holds, then
holds, then  and
and  for
for  where
where 
Theorems 4.26–4.32 are obtained in [25]. For some improvements and/or generalizations, see [32–35].
Theorem 4.26.
Assume that conditions  and
and  of Lemma 4.25 hold, and there exists a positive integer
of Lemma 4.25 hold, and there exists a positive integer  such that
such that  for
for  If
If

then every solution of (4.73) is oscillatory.
Proof.
Without loss of generality, we can assume  If (4.73) has a nonoscillatory solution
If (4.73) has a nonoscillatory solution  we might as well assume
we might as well assume  From Lemma 4.25,
From Lemma 4.25,  for
for  where
where  Let
Let

Then,  Using condition (i) in (4.73), we get for
Using condition (i) in (4.73), we get for 

Using condition (ii) and  yield
yield

From the above inequalities, we have

where  Taking
Taking  and
and  we get
we get

By induction, for any natural number  we obtain
we obtain

Since,  above inequality and the hypothesis lead to a contradiction. So, every solution of (4.73) oscillatory.
above inequality and the hypothesis lead to a contradiction. So, every solution of (4.73) oscillatory.
From Theorem 4.26, the following corollary is immediate.
Corollary 4.27.
Assume that conditions  of Lemma 4.25 hold and there exists a positive integer
of Lemma 4.25 hold and there exists a positive integer  such that
such that  for
for  If
If

then every solution of (4.73) is oscillatory.
The proof of the following theorem is similar to that of Theorem 4.26.
Theorem 4.28.
Assume that conditions  and
and  of Lemma 4.25 hold and
of Lemma 4.25 hold and  for any
for any  If
If

then every solution of (4.73) is oscillatory.
Corollary 4.29.
Assume that conditions  and
and  of Lemma 4.25 hold and
of Lemma 4.25 hold and  for any
for any  Suppose that there exist a positive integer
Suppose that there exist a positive integer  and a constant
and a constant  such that
such that

If  then every solution of (4.73) is oscillatory.
then every solution of (4.73) is oscillatory.
Example 4.30.
Consider the superlinear equation:

where  is a natural number. Since
is a natural number. Since  ,
,  ,
,  and
and  It is easy to see that conditions (i), (ii), and (iii) are satisfied. Moreover
It is easy to see that conditions (i), (ii), and (iii) are satisfied. Moreover

Hence, by Corollary 4.29, we find that every solution of (4.85) is oscillatory. On the other hand, by Theorem 2.6, it follows that (4.85) without impulses is nonoscillatory.
Theorem 4.31.
Assume that conditions (i), (ii), and (iii) of Lemma 4.25 hold, and there exists a positive integer  such that
such that  for
for  If
If

then every solution of (4.73) is oscillatory.
Proof.
Without loss of generality, let  If (4.1) has a nonoscillatory solution
If (4.1) has a nonoscillatory solution  assume
assume  By Lemma 4.25,
By Lemma 4.25,  Since
Since  we have
we have

It is easy to see that  is monotonically nondecreasing in
is monotonically nondecreasing in  Now (4.73) yields
Now (4.73) yields

Hence, from the above inequality and condition (ii), we find that

Generally, for any natural number  we have
we have

By (4.89) and (4.91), noting  and
and  for any natural number
for any natural number  we obtain
we obtain

Note that  and
and  is nondecreasing. Dividing the above inequality by
is nondecreasing. Dividing the above inequality by  and then integrating from
and then integrating from  to
to  we get
we get

Since (4.88) holds, the above inequality yields

The above inequality and the hypotheses lead to a contradiction. So, every solution of (4.73) is oscillatory.
The proof of the following theorem is similar to that of Theorem 4.31.
Theorem 4.32.
Assume that conditions  of Lemma 4.25 hold, and there exists a positive integer
of Lemma 4.25 hold, and there exists a positive integer  such that
such that  for
for  Suppose that
Suppose that  for any
for any  and
and

Then, every solution of (4.73) is oscillatory.
In [36], the author studied the second-order nonlinear impulsive differential equations of the following form:

where  and
and  ,
,  .
.
Sufficient conditions are obtained for oscillation of (4.96) by using integral averaging technique. In particular the Philos type oscillation criteria are extended to impulsive differential equations.
It is assumed that
-
(i)
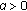 is a constant;
is a constant; -
(ii)
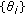 is a strictly increasing unbounded sequence of real numbers;
is a strictly increasing unbounded sequence of real numbers; 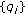 is a real sequence;
is a real sequence; -
(iii)
 ,
, 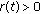 ;
; -
(iv)
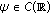 ,
, 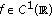 with
with  ,
,  for
for 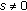 and
and 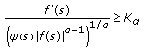 (4.97)
(4.97)
is satisfied;  is a constant.
is a constant.
In order to prove the results the following well-known inequality is needed [26].
Lemma 4.33.
If  ,
,  are nonnegative numbers, then
are nonnegative numbers, then

and the equality holds if and only if  .
.
The following theorem is one of the main results of this study.
Theorem 4.34 (see [36]).
Let  and
and  . Assume that
. Assume that  ,
,  satisfy the following conditions.
satisfy the following conditions.
-
(i)
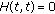 for
for 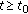 and
and  on
on 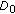 .
. -
(ii)
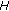 has a continuous and nonpositive partial derivative on
has a continuous and nonpositive partial derivative on  with respect to the second variable.
with respect to the second variable. -
(iii)
One has
 (4.99)
(4.99)
If

where  , then (4.96) is oscillatory.
, then (4.96) is oscillatory.
Proof.
Let  be a nonoscillatory solution of (4.96). We assume that
be a nonoscillatory solution of (4.96). We assume that  on
on  for some sufficiently large
for some sufficiently large  . Define
. Define

Differentiating (4.101) and making use of (4.96) and (4.97), we obtain


Replacing  by
by  in (4.102) and multiplying the resulting equation by
in (4.102) and multiplying the resulting equation by  and integrating from
and integrating from  to
to  , we get
, we get

Integrating by parts and using (4.103), we find

Combining (4.104) and (4.105), we obtain

Using inequality (4.98) with 

we find

From (4.106) and (4.108), we obtain

for all  . In the above inequality we choose
. In the above inequality we choose  , to get
, to get

Thus, it follows that

which contradicts (4.100). This completes the proof.
As a corollary to Theorem 4.34, we have the following result.
Corollary 4.35.
Let condition (4.100) in Theorem 4.34 be replaced by

then (4.96) is oscillatory.
Note that in the special case of half-linear equations, for  and
and  , the condition (4.97) is satisfied with
, the condition (4.97) is satisfied with  .
.
The proof of the following theorem can be accomplished by using the method developed for the nonimpulsive case and similar arguments employed in the proof of Theorem 4.34.
Theorem 4.36 (see [36]).
Let the functions  and
and  be defined as in Theorem 4.34. Moreover, Suppose that
be defined as in Theorem 4.34. Moreover, Suppose that

If there exists a function  such that
such that

and for every 

where  , then (4.96) is oscillatory.
, then (4.96) is oscillatory.
4.4. Higher-Order Nonlinear Equations
There are only a very few works concerning the oscillation of higher-order nonlinear impulsive differential equations [37–40].
In [37] authors considered even order impulsive differential equations of the following form

where

Let the following conditions hold.
 for
for  for
for  , where
, where  is positive and continuous on
is positive and continuous on  for
for 
 , and there exist positive numbers
, and there exist positive numbers  such that
such that

A function  is said to be a solution of (4.116), if (i)
is said to be a solution of (4.116), if (i)  ; (ii) for
; (ii) for  and
and  satisfies
satisfies  ; (iii)
; (iii)  is left continuous on
is left continuous on  and
and 
The first two theorems can be considered as modifications of Theorems 3.43 and 4.26, respectively.
Theorem 4.37 (see [37]).
If conditions  and
and  hold,
hold,  ,
,  , and if
, and if

then every bounded solution of (4.116) is oscillatory.
Theorem 4.38 (see [37]).
If conditions  and
and  hold,
hold,  and
and

then every solution of (4.116) is oscillatory.
Theorem 4.39 (see [37]).
If conditions (A) and (B) hold, 
 ,
,  , and for any
, and for any  ,
,

then every solution of (4.116) is oscillatory.
Corollary 4.40.
Assume that conditions (A) and (B) hold, and that  ,
,  . If
. If

then every solution of (4.116) is oscillatory.
Corollary 4.41.
Assume that conditions (A) and (B) hold, and that there exists a positive number  , such that
, such that  ,
,  . If
. If

then every solution of (4.116) is oscillatory.
Example 4.42.
Consider the impulsive differential equation:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
It is easy to verify conditions of Theorem 4.38. So every solution of (4.124) is oscillatory.
Example 4.43.
Consider the impulsive differential equation:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
In this case, it can be show that conditions of Corollary 4.41 are satisfied. Thus, every solution of (4.125) is oscillatory.
In [40], the authors considered the impulsive differential equations with piecewise constant argument of the following form:

where  is the set of all positive integers,
is the set of all positive integers,  ,
,  and
and  are given positive constants,
are given positive constants,  denotes the set of maximum integers, and
denotes the set of maximum integers, and  for all
for all  . It is assumed that
. It is assumed that
-
(i)
 ;
; -
(ii)
for any
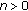 and all
and all  ,
,  (4.127)
(4.127)
-
(iii)
there exists
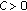 such that
such that 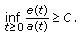 (4.128)
(4.128)
Theorem 4.44 (see [40]).
Assume that conditions  ,
,  , and
, and  hold. Moreover, suppose that for any
hold. Moreover, suppose that for any  , there exists a
, there exists a  such that
such that

where  . Then every solution of (4.126) is oscillatory.
. Then every solution of (4.126) is oscillatory.
Theorem 4.45 (see [40]).
Assume that conditions  and
and  hold. Moreover, suppose that for any
hold. Moreover, suppose that for any  , there exists a
, there exists a  such that
such that

Then every solution of (4.126) is oscillatory.
Example 4.46.
Consider the impulsive differential equation:

It is easy to verify that conditions of Theorem 4.45 are all satisfied. Therefore every solution of (4.131) is oscillatory.
References
Bainov DD, Simeonov PS: Oscillation Theory of Impulsive Differential Equations. International Publications, Orlando, Fla, USA; 1998:ii+284.
Baĭnov DD, Simeonov PS: Impulsive Differential Equations: Asymptotic Properties of the Solutions, Series on Advances in Mathematics for Applied Sciences. Volume 28. World Scientific, Singapore; 1995:xii+230.
Bainov D, Covachev V: Impulsive Differential Equations with a Small Parameter, Series on Advances in Mathematics for Applied Sciences. Volume 24. World Scientific, Singapore; 1994:x+268.
Bainov DD, Simeonov PS: Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, Harlow, UK; 1993.
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific, Singapore; 1989:xii+273.
Samoilenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 14. World Scientific, Singapore; 1995:x+462.
Kruger-Thiemer E: Formal theory of drug dosage regiments I. Journal of Theoretical Biology 1966, 13: 212-235. 10.1016/0022-5193(66)90018-X
Pierce JG, Schumitzky A: Optimal impulsive control of compartment models. I. Qualitative aspects. Journal of Optimization Theory and Applications 1976,18(4):537-554. 10.1007/BF00932661
Gopalsamy K, Zhang BG: On delay differential equations with impulses. Journal of Mathematical Analysis and Applications 1989,139(1):110-122. 10.1016/0022-247X(89)90232-1
Bainov DD, Domshlak YI, Simeonov PS: Sturmian comparison theory for impulsive differential inequalities and equations. Archiv der Mathematik 1996,67(1):35-49. 10.1007/BF01196165
Wu S, Duan Y: Oscillation, stability, and boundedness of second-order differential systems with random impulses. Computers & Mathematics with Applications 2005,49(9-10):1375-1386. 10.1016/j.camwa.2004.12.009
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Second Order Dynamic Equations, Series in Mathematical Analysis and Applications. Volume 5. Taylor' Francis, London, UK; 2003:viii+404.
Hille E: Non-oscillation theorems. Transactions of the American Mathematical Society 1948, 64: 234-252. 10.1090/S0002-9947-1948-0027925-7
Leighton W: On self-adjoint differential equations of second order. Journal of the London Mathematical Society 1952, 27: 37-47. 10.1112/jlms/s1-27.1.37
Atkinson FV: On second-order non-linear oscillations. Pacific Journal of Mathematics 1955, 5: 643-647.
Özbekler A, Zafer A: Sturmian comparison theory for linear and half-linear impulsive differential equations. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):289-297. 10.1016/j.na.2005.01.087
Özbekler A, Zafer A: Picone's formula for linear non-selfadjoint impulsive differential equations. Journal of Mathematical Analysis and Applications 2006,319(2):410-423. 10.1016/j.jmaa.2005.06.019
Özbekler A, Zafer A: Forced oscillation of super-half-linear impulsive differential equations. Computers & Mathematics with Applications 2007,54(6):785-792. 10.1016/j.camwa.2007.03.003
Shen J: Qualitative properties of solutions of second-order linear ODE with impulses. Mathematical and Computer Modelling 2004,40(3-4):337-344. 10.1016/j.mcm.2003.12.009
Luo Z, Shen J: Oscillation of second order linear differential equations with impulses. Applied Mathematics Letters 2007,20(1):75-81. 10.1016/j.aml.2006.01.019
Huang C: Oscillation and nonoscillation for second order linear impulsive differential equations. Journal of Mathematical Analysis and Applications 1997,214(2):378-394. 10.1006/jmaa.1997.5572
Wan A, Mao W: Oscillation and asymptotic stability behavior of a third order linear impulsive equation. Journal of Applied Mathematics & Computing 2005,18(1-2):405-417. 10.1007/BF02936583
Chen YS, Feng WZ: Oscillations of higher-order linear ODEs with impulses. Journal of South China Normal University. Natural Science Edition 2003, (3):14-19.
Feng W: Oscillations of fourth order ODE with impulses. Annals of Differential Equations 2003,19(2):136-145.
Chen YS, Feng WZ: Oscillations of second order nonlinear ODE with impulses. Journal of Mathematical Analysis and Applications 1997,210(1):150-169. 10.1006/jmaa.1997.5378
Hardy GH, Littlewood JE, Pólya G: Inequalities. Cambridge University Press, Cambridge, UK; 1934.
Liu X, Xu Z: Oscillation of a forced super-linear second order differential equation with impulses. Computers & Mathematics with Applications 2007,53(11):1740-1749. 10.1016/j.camwa.2006.08.040
Graef JR, Karsai J: Intermittant and impulsive effects in second order systems. Nonlinear Analysis: Theory, Methods & Applications 1997, 30: 1561-1571. 10.1016/S0362-546X(97)00029-1
Graef JR, Karsai J: Oscillation and nonoscillation in nonlinear impulsive systems with increasing energy. Proceedings of the International Conference on Dynamical Systems and Differential Equations, 2000, Atlanta, Ga, USA
Graef JR, Karsai J: On the oscillation of impulsively damped halflinear oscillators. In Proceedings of the 6th Colloquium on the Qualitative Theory of Differential Equations (Szeged, '99), 2000. Electronic Journal of Qualitative Theory of Differential Equations; 1-12.
Özbekler A, Zafer A: Interval criteria for the forced oscillation of super-half-linear differential equations under impulse effects. Mathematical and Computer Modelling 2009,50(1-2):59-65. 10.1016/j.mcm.2008.10.020
Luo J, Debnath L: Oscillations of second-order nonlinear ordinary differential equations with impulses. Journal of Mathematical Analysis and Applications 1999,240(1):105-114. 10.1006/jmaa.1999.6596
Xiu-li W, Si-Yang C, Ji H: Oscillation of a class of second-order nonlinear ODE with impulses. Applied Mathematics and Computation 2003,138(2-3):181-188. 10.1016/S0096-3003(02)00073-5
Luo J: Second-order quasilinear oscillation with impulses. Computers & Mathematics with Applications 2003,46(2–3):279-291. 10.1016/S0898-1221(03)90031-9
He Z, Ge W: Oscillations of second-order nonlinear impulsive ordinary differential equations. Journal of Computational and Applied Mathematics 2003,158(2):397-406. 10.1016/S0377-0427(03)00474-6
Özbekler A: Oscillation criteria for second order nonlinear impulsive differential equations, further progress in analysis. In Proceedings of the 6th International ISAAC Congress, 2009, Ankara, Turkey. World Scientific; 545-554.
Zhang C, Feng W: Oscillation for higher order nonlinear ordinary differential equations with impulses. Electronic Journal of Differential Equations 2006, (18):1-12.
Pan LJ, Wang GQ, Cheng SS: Oscillation of even order nonlinear differential equations with impulses. Funkcialaj Ekvacioj 2007,50(1):117-131. 10.1619/fesi.50.117
Dimitrova MB: Nonoscillation of the solutions of impulsive differential equations of third order. Journal of Applied Mathematics and Stochastic Analysis 2001,14(3):309-316. 10.1155/S1048953301000272
Fu X, Li X: Oscillation of higher order impulsive differential equations of mixed type with constant argument at fixed time. Mathematical and Computer Modelling 2008,48(5-6):776-786. 10.1016/j.mcm.2007.11.006
Acknowledgments
This work was done when the second author was on academic leave, visiting Florida Institute of Technology. The financial support of The Scientific and Technological Research Council of Turkey (TUBITAK) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R., Karakoç, F. & Zafer, A. A Survey on Oscillation of Impulsive Ordinary Differential Equations. Adv Differ Equ 2010, 354841 (2010). https://doi.org/10.1155/2010/354841
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/354841
 has infinitely many negative terms.
has infinitely many negative terms.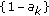 has finitely many negative terms.
has finitely many negative terms.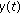 such that
such that 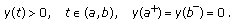

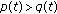 in a subinterval of
in a subinterval of 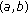 or
or 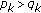 for some
for some 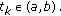
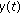 such that
such that 
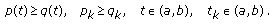
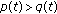 in some subinterval of
in some subinterval of 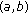 or
or 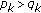 for some
for some 
 of (3.6) for which
of (3.6) for which  has at least one zero in
has at least one zero in 
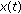 of (3.6) has at least one zero in
of (3.6) has at least one zero in 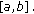
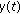 of (3.7) and a sequence of disjoint intervals
of (3.7) and a sequence of disjoint intervals 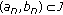 such that
such that 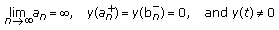
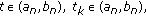 and
and  ;
; 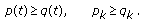
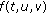 is such that if
is such that if  is a continuous function for
is a continuous function for  having a piecewise continuous derivative
having a piecewise continuous derivative  for
for  then the function
then the function  is piecewise continuous for
is piecewise continuous for 
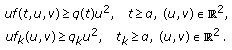
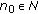 such that
such that 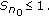
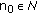 such that
such that 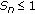 for all
for all 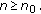
 for all
for all  and
and 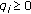 for all
for all 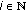 for which
for which  ;
; ,
,  ,
,  ,
, 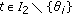 ;
;  ,
, 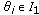 ,
,  ,
,  for all
for all 
 and
and  where
where  ,
, 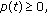 and
and 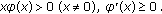
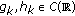 , and there exist positive numbers
, and there exist positive numbers 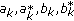 such that
such that 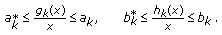
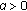 is a constant;
is a constant;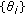 is a strictly increasing unbounded sequence of real numbers;
is a strictly increasing unbounded sequence of real numbers; 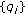 is a real sequence;
is a real sequence; ,
, 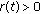 ;
;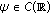 ,
, 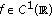 with
with  ,
,  for
for 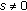 and
and 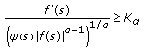
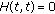 for
for 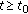 and
and  on
on 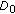 .
.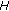 has a continuous and nonpositive partial derivative on
has a continuous and nonpositive partial derivative on  with respect to the second variable.
with respect to the second variable.
 ;
;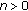 and all
and all  ,
, 
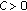 such that
such that