- Research Article
- Open access
- Published:
Structure of Eigenvalues of Multi-Point Boundary Value Problems
Advances in Difference Equations volume 2010, Article number: 381932 (2010)
Abstract
The structure of eigenvalues of  ,
,  , and
, and  , will be studied, where
, will be studied, where  ,
,  , and
, and  . Due to the nonsymmetry of the problem, this equation may admit complex eigenvalues. In this paper, a complete structure of all complex eigenvalues of
. Due to the nonsymmetry of the problem, this equation may admit complex eigenvalues. In this paper, a complete structure of all complex eigenvalues of  this equation will be obtained. In particular, it is proved that this equation has always a sequence of real eigenvalues tending to
this equation will be obtained. In particular, it is proved that this equation has always a sequence of real eigenvalues tending to  . Moreover, there exists some constant
. Moreover, there exists some constant  depending on
depending on  , such that when
, such that when  satisfies
satisfies  , all eigenvalues of this equation are necessarily real.
, all eigenvalues of this equation are necessarily real.
1. Introduction
In the recent years, multi-point boundary value problems of ordinary differential equations have received much attention.Some remarkable results have been obtained,especially for the existence and multiplicity of (positive) solutions for nonlinear second-order ordinary differential equations [1–10]. However, as noted in [5, 6], although it is important in many nonlinear problems, the corresponding eigenvalue theory for linear problems is incomplete. The main reason is that the linear operators are no longer symmetric with respect to multi-point boundary conditions.
In this paper, we will establish some fundamental results for eigenvalue theory of multi-point boundary value problems. Precisely, for a real potential  , we consider the eigenvalue problem
, we consider the eigenvalue problem

associated with the  -point boundary condition
-point boundary condition

Here  and the boundary data are
and the boundary data are  and
and

As usual,  is called an eigenvalue of (1.1) and (1.2) if (1.1) has a nonzero complex solution
is called an eigenvalue of (1.1) and (1.2) if (1.1) has a nonzero complex solution  satisfying conditions of (1.2). The set of all eigenvalues of problem (1.1) and (1.2) is denoted by
satisfying conditions of (1.2). The set of all eigenvalues of problem (1.1) and (1.2) is denoted by  called the spectrum.
called the spectrum.
When  , boundary condition (1.2) is reduced to the Dirichlet boundary condition
, boundary condition (1.2) is reduced to the Dirichlet boundary condition

Problem (1.1)–(1.4) is symmetric and has only real eigenvalues [11, 12]. However, in case  , problem (1.1) and (1.2) is not symmetric, thus
, problem (1.1) and (1.2) is not symmetric, thus  may contain nonreal eigenvalues. A simple example is given by Example 2.1.
may contain nonreal eigenvalues. A simple example is given by Example 2.1.
When  , (1.1) is
, (1.1) is

Eigenvalues of problem (1.5)–(1.2) can be analyzed using elementary method, because all solutions of (1.5) can be found explicitly. However, as far as the authors know, even for this simple eigenvalue problem, the spectrum theory is incomplete in the literature. In [5, 6], Ma and O'Regan have constructed allreal eigenvalues of problem (1.5)–(1.2) when all  are rational, and
are rational, and  satisfies certain nondegeneracy condition. In [8, 9], Rynne has obtained all real eigenvalues for general
satisfies certain nondegeneracy condition. In [8, 9], Rynne has obtained all real eigenvalues for general  . See [13] for further extension.
. See [13] for further extension.
The main topic of this paper is the structure of  . Much attention will be paid to the real eigenvalues due to important applications in nonlinear problems.
. Much attention will be paid to the real eigenvalues due to important applications in nonlinear problems.
Theorem 1.1.
Given  and
and  , then
, then  is composed of a sequence
is composed of a sequence  which satisfies
which satisfies

Theorem 1.2.
Given  and
and  , then
, then  , where
, where

For  , the norm is
, the norm is  . For
. For  , the
, the  norm is denoted by
norm is denoted by  . With some restrictions on
. With some restrictions on  , we are able to prove that
, we are able to prove that  contains only real eigenvalues.
contains only real eigenvalues.
Theorem 1.3.
If  satisfies
satisfies  , then the spectrum
, then the spectrum  contains at most finitely many nonreal eigenvalues.
contains at most finitely many nonreal eigenvalues.
Theorem 1.4.
Given  , there exists some constant
, there exists some constant  , depending on the norm
, depending on the norm  only, such that if
only, such that if  satisfies
satisfies  , then one has
, then one has  .
.
To sketch our proofs, let us denote

Basically, eigenvalues of  are zeros of some entire functions. See (2.24) and (3.3). In order to study the distributions of eigenvalues, we will consider
are zeros of some entire functions. See (2.24) and (3.3). In order to study the distributions of eigenvalues, we will consider  as a perturbation of
as a perturbation of  or of
or of  . To obtain the existence of infinitely many real eigenvalues as in Theorem 1.2, some properties of almost periodic functions [14, 15] will be used. See Lemmas 2.3 and 3.2. In order to pass the results of
. To obtain the existence of infinitely many real eigenvalues as in Theorem 1.2, some properties of almost periodic functions [14, 15] will be used. See Lemmas 2.3 and 3.2. In order to pass the results of  to general potentials
to general potentials  , many techniques like implicit function theorem and the Rouché theorem will be exploited. Moreover, some basic estimates in [11] for fundamental solutions of (1.1) play an important role, especially in the proofs of Theorems 1.3 and 1.4. Due to the non-symmetry of problem
, many techniques like implicit function theorem and the Rouché theorem will be exploited. Moreover, some basic estimates in [11] for fundamental solutions of (1.1) play an important role, especially in the proofs of Theorems 1.3 and 1.4. Due to the non-symmetry of problem  , the proofs are complicated than that in [11] where the Dirichlet problem is considered.
, the proofs are complicated than that in [11] where the Dirichlet problem is considered.
The paper is organized as follows. In Section 2, we will give some detailed analysis on problem  . In Section 3, after developing some basic estimates, we will prove Theorems 1.1 and 1.2. In Section 4, we will develop some techniques to exclude nonreal eigenvalues and complete the proofs of Theorems 1.3 and 1.4. Some open problem on the spectrum of
. In Section 3, after developing some basic estimates, we will prove Theorems 1.1 and 1.2. In Section 4, we will develop some techniques to exclude nonreal eigenvalues and complete the proofs of Theorems 1.3 and 1.4. Some open problem on the spectrum of  will be mentioned.
will be mentioned.
2. Structure of Eigenvalues of the Zero Potential
In order to motivate our consideration for  with non-zero potentials
with non-zero potentials  , in this section we consider the spectrum
, in this section we consider the spectrum  with the zero potential.
with the zero potential.
2.1. An Example of Nonreal Eigenvalues
Let  . Boundary condition (1.2) is the following three-point boundary condition:
. Boundary condition (1.2) is the following three-point boundary condition:

where  and
and  . We consider the eigenvalue problems (1.5)–(2.1).
. We consider the eigenvalue problems (1.5)–(2.1).
Let  . Complex solutions
. Complex solutions  of (1.5) satisfying
of (1.5) satisfying  are
are  ,
,  , where
, where

Notice that  is an entire function of
is an entire function of  . Define
. Define

Obviously,  depends on the boundary data
depends on the boundary data  as well. Then
as well. Then  if and only if
if and only if  satisfies
satisfies

Example 2.1.
Let  . By (2.3) and (2.4),
. By (2.3) and (2.4),  if and only if
if and only if  satisfies
satisfies

That is, either

or

Equation (2.6) shows that  always contains positive eigenvalues
always contains positive eigenvalues  ,
,  .
.
Equation (2.7) has real solutions  if and only if
if and only if  . In this case,
. In this case,  consists of non-negative eigenvalues. More precisely,
consists of non-negative eigenvalues. More precisely,

Equation (2.7) has nonreal solutions  if and only if
if and only if  . In this case, we have
. In this case, we have

For example, one has


Notice that all eigenvalues obtained from (2.7) can be constructed explicitly as (2.10) and (2.11). For example,  contains negative eigenvalues if and only if
contains negative eigenvalues if and only if  . Moreover, in this case, one has the unique negative eigenvalue given by
. Moreover, in this case, one has the unique negative eigenvalue given by

For more details, see [5, 6, 8].
Results (2.10) and (2.11) show that to guarantee that  contains only real eigenvalues, some restrictions on parameters
contains only real eigenvalues, some restrictions on parameters  are necessary.
are necessary.
2.2. Real Eigenvalues with General Parameters
In the following we consider general  , based on properties of almost periodic functions [14, 15].
, based on properties of almost periodic functions [14, 15].
Definition 2.2.
Suppose that  is a bounded continuous function. One calls that
is a bounded continuous function. One calls that  is almost periodic, if for any
is almost periodic, if for any  , there exists
, there exists  such that for any
such that for any  , there exists
, there exists  such that
such that

Any almost periodic function  admits a well-defined mean value
admits a well-defined mean value

To study  and
and  , let us prove some properties on almost periodic functions.
, let us prove some properties on almost periodic functions.
Lemma 2.3.
Let  be an almost periodic function.
be an almost periodic function.
-
(i)
For any
 , one has
, one has 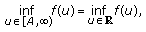 (2.15)
(2.15)

-
(ii)
Assume that
 is non-zero and
is non-zero and 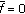 . Then
. Then 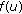 is oscillatory as
is oscillatory as  , that is,
, that is, 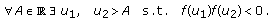 (2.17)
(2.17)
In particular,  has a sequence of positive zeros tending to
has a sequence of positive zeros tending to  .
.
Proof.
-
(i)
Let us only prove (2.15) because (2.16) is similar. For any
 , choose
, choose  such that
such that  (2.18)
(2.18)
By (2.13), there exists  such that
such that  . For any
. For any  , let us take
, let us take

By (2.13) again, there exists  such that
such that  . Hence
. Hence

In particular,

By the choice of  , one has
, one has  . Hence
. Hence

This proves (2.15).
-
(ii)
If
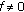 and
and 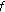 has mean value
has mean value  , it is easy to see that
, it is easy to see that 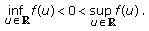 (2.23)
(2.23)
Now result (2.17) can be deduced simply from (2.15) and (2.16).
Like (2.3) and (2.4), all eigenvalues  of problem
of problem  are determined by the following equation:
are determined by the following equation:

where

Notice that  is an entire function of
is an entire function of  . Hence (2.24) has only isolated zeros in
. Hence (2.24) has only isolated zeros in  . For
. For  , we have the following elementary equalities:
, we have the following elementary equalities:

For real eigenvalues of problem  , we have the following result.
, we have the following result.
Lemma 2.4.
Given  , then
, then  , where
, where

Proof.
Let us first consider possible positive eigenvalues  of
of  , where
, where  . By the first equality of (2.26), equation (2.24) is the same as
. By the first equality of (2.26), equation (2.24) is the same as

The function  is a non-zero, almost periodic function and has mean value
is a non-zero, almost periodic function and has mean value  . In fact,
. In fact,  is quasiperiodic. By Lemma 2.3(ii),
is quasiperiodic. By Lemma 2.3(ii),  has infinitely many positive zeros tending to
has infinitely many positive zeros tending to  . See Figure 1. Hence
. See Figure 1. Hence  contains a sequence of positive eigenvalues tending to
contains a sequence of positive eigenvalues tending to  .
.
Next we consider possible negative eigenvalues  of
of  , where
, where  . In this case, (2.24) is the same as
. In this case, (2.24) is the same as

See the first equality of (2.26). Notice that  is analytic in
is analytic in  . As
. As  , one has
, one has

Thus (2.29) has at most finitely many positive solutions. Hence  contains at most finitely many negative eigenvalues.
contains at most finitely many negative eigenvalues.
As both (2.28) and (2.29) have only isolated solutions, the above two cases show that all real eigenvalues of  can be listed as in (2.27).
can be listed as in (2.27).
The quasi-periodic function  is as in Figure 1.
is as in Figure 1.
2.3. Nonexistence of Nonreal Eigenvalues
To study real eigenvalues of problem  , the authors of [5, 6, 8] have imposed some restrictions on
, the authors of [5, 6, 8] have imposed some restrictions on  . The typical conditions are
. The typical conditions are

With some restrictions on  , we will prove that
, we will prove that  consists of only real eigenvalues.
consists of only real eigenvalues.
Lemma 2.5.
Suppose that  satisfies
satisfies

Then  contains only real eigenvalues. Moreover, one has
contains only real eigenvalues. Moreover, one has  .
.
Proof.
When  , problem (1.5)–(1.2) is the Dirichlet problem and
, problem (1.5)–(1.2) is the Dirichlet problem and  . In the following, assume that
. In the following, assume that  .
.
Suppose that  , where
, where  ,
,  . We assert that
. We assert that  under assumption (2.32). Otherwise, assume that
under assumption (2.32). Otherwise, assume that  . By (2.26), equation (2.24) is the following system for
. By (2.26), equation (2.24) is the following system for  :
:

It follows from the Hölder inequality that

which is impossible under assumption (2.32). Thus  and therefore
and therefore  .
.
Next, by (2.2), (2.25), and the Hölder inequality, we have

because  and
and  . By (2.24),
. By (2.24),  . Hence we have
. Hence we have  .
.
Finally, by the Hölder inequality, assumption (2.32) implies that  . For any
. For any  , the function
, the function  of (2.28) satisfies
of (2.28) satisfies

Hence (2.28) shows that  .
.
Remark 2.6.
Condition (2.32) is sharp. For example, let  and
and  . Example 2.1 shows that
. Example 2.1 shows that  contains nonreal eigenvalues if
contains nonreal eigenvalues if  . Similarly, by letting
. Similarly, by letting  and
and  , one can verify that
, one can verify that  contains nonreal eigenvalues when
contains nonreal eigenvalues when  .
.
3. Structure of Eigenvalues of Non-Zero Potentials
Given  and complex parameter
and complex parameter  , the fundamental solutions of (1.1) are denoted by
, the fundamental solutions of (1.1) are denoted by  ,
,  . That is, they are solutions of (1.1) satisfying the initial values
. That is, they are solutions of (1.1) satisfying the initial values

Notice that  are entire functions of
are entire functions of  . See [11]. To study
. See [11]. To study  , let us introduce
, let us introduce

which is an entire function of  . See (2.25) for the case
. See (2.25) for the case  . Notice that
. Notice that  is real for
is real for  . Then
. Then  if and only if
if and only if

3.1. Basic Estimates
Lemma 3.1.
Given  , one has
, one has

uniformly in  .
.
Proof.
Suppose that  . We have from (2.26)
. We have from (2.26)

The uniform limits in (3.4) are evident.
For the function  of (2.28), one has the following result on its amplitude.
of (2.28), one has the following result on its amplitude.
Lemma 3.2.
Given  , there exist a constant
, there exist a constant  and a sequence
and a sequence  of increasing positive numbers such that
of increasing positive numbers such that  and
and

Proof.
Recall that  is quasi-periodic and has the mean value
is quasi-periodic and has the mean value  . Denote that
. Denote that

Then  . The construction for
. The construction for  is as follows. By (2.15), one has some
is as follows. By (2.15), one has some  such that
such that  . By letting
. By letting  in (2.16), we have some
in (2.16), we have some  such that
such that  . Then, by letting
. Then, by letting  in (2.15), we have some
in (2.15), we have some  such that
such that  . Inductively, we can use (2.15) and (2.16) to find a sequence
. Inductively, we can use (2.15) and (2.16) to find a sequence  such that
such that  , and (3.6) is satisfied for all
, and (3.6) is satisfied for all  .
.
Lemma 3.3 (basic estimates, [11, page 13, Theorem  ]).
]).
Let  and
and  . There hold the following estimates for all
. There hold the following estimates for all 




Remark 3.4.
For their purpose, the authors of [11] have proved (3.8)–(3.11) for complex potentials  . For example, in (3.8)–(3.11), the terms
. For example, in (3.8)–(3.11), the terms  and
and  are replaced by
are replaced by  and
and  , respectively in [11]. Inspecting their proofs, especially the proof of [11, pages 7–9, Theorem
, respectively in [11]. Inspecting their proofs, especially the proof of [11, pages 7–9, Theorem  ], one can find that estimates (3.8)–(3.11) are also true for
], one can find that estimates (3.8)–(3.11) are also true for  potentials
potentials  . Moreover, these estimates can be established even for linear measure differential equations with general measures [16]. By the Hölder inequality, one has
. Moreover, these estimates can be established even for linear measure differential equations with general measures [16]. By the Hölder inequality, one has

This is why the authors of [11] have used these terms in (3.8)–(3.11).
Lemma 3.5.
There holds the following estimate for  :
:

where

Proof.
Define  . From (3.9), we have
. From (3.9), we have

By (2.25) and (3.2), we have

This gives (3.13).
Lemma 3.6.
One has  on
on  . Consequently, there exists
. Consequently, there exists  such that
such that  .
.
Proof.
Otherwise, we have  on
on  . Notice that
. Notice that

Let  in (3.13), where
in (3.13), where  is as in Lemma 3.2. We have
is as in Lemma 3.2. We have

Hence  , a contradiction with (3.6).
, a contradiction with (3.6).
3.2. Eigenvalues with General Parameters
The most general results on spectrum  of
of  are stated as in Theorem 1.1.
are stated as in Theorem 1.1.
Proof of Theorem 1.1.
We argue as in general spectrum theory [12]. By Lemma 3.6, there exists  such that
such that  . That is, the following equation:
. That is, the following equation:

has only the trivial solution  satisfying boundary condition (1.2). Let
satisfying boundary condition (1.2). Let  be the Green function associated with problem (3.19)-(1.2). Then
be the Green function associated with problem (3.19)-(1.2). Then  if and only if
if and only if  and
and

has nontrivial solution  satisfying (1.2). In other words,
satisfying (1.2). In other words,  if and only if the following equation:
if and only if the following equation:

has non-trivial solution  , where
, where

Since  is a compact linear operator, one sees that this happens when and only when
is a compact linear operator, one sees that this happens when and only when  , where
, where  is the spectrum of
is the spectrum of  . Hence
. Hence  consists of a sequence of eigenvalues which can accumulate only at infinity of
consists of a sequence of eigenvalues which can accumulate only at infinity of  .
.
For  , denote that
, denote that

Suppose that  and
and  . Then
. Then  and (3.13) implies that
and (3.13) implies that

We conclude that all non-zero eigenvalues  satisfy
satisfy

Let us derive some consequences from estimate (3.25) for  .
.
-
(i)
Since
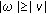 , it follows from the uniform limits in (3.4) that
, it follows from the uniform limits in (3.4) that  (3.26)
(3.26)
Thus there exists some  such that
such that

The horizontal strip  of (3.27) in the
of (3.27) in the  -plane is transformed by (3.23) to the following half-plane
-plane is transformed by (3.23) to the following half-plane  in the
in the  -plane:
-plane:

 Let
Let  . We assert that
. We assert that

contains at most finitely many eigenvalues. Otherwise, suppose that

contains infinitely many  . Since (3.3) has only isolated solutions, we have necessarily
. Since (3.3) has only isolated solutions, we have necessarily  . By denoting
. By denoting  , one has
, one has

In particular,  . Now estimate (3.25) reads as
. Now estimate (3.25) reads as

This is impossible because we have the uniform limits (3.4).
Combining (i) and (ii), we know that  can be listed as in (1.6).
can be listed as in (1.6).
Though problem  is not symmetric,
is not symmetric,  always contains infinitely many real eigenvalues, as stated in Theorem 1.2.
always contains infinitely many real eigenvalues, as stated in Theorem 1.2.
Proof of Theorem 1.2.
We need to only consider positive eigenvalues of  . Let
. Let  in (3.13), where
in (3.13), where  is as in Lemma 3.2. By using (3.17), we have
is as in Lemma 3.2. By using (3.17), we have

Since  , w.l.o.g., we can assume that
, w.l.o.g., we can assume that  for all
for all  . Thus
. Thus

By using (3.6), we conclude that

Hence (3.3) has at least one positive solution  in each interval
in each interval  ,
,  . Combining with Theorem 1.1,
. Combining with Theorem 1.1,  consists of a sequence of real eigenvalues tending to
consists of a sequence of real eigenvalues tending to  . Hence
. Hence  can be listed as in (1.7).
can be listed as in (1.7).
4. Nonexistence of Nonreal Eigenvalues for Small 
We will apply the Rouché theorem to give further results on  when
when  is small, following the approach in [11] for the Dirichlet problem (1.1)-(1.4), which corresponds to
is small, following the approach in [11] for the Dirichlet problem (1.1)-(1.4), which corresponds to  with
with  . Let us recall the Rouché theorem.
. Let us recall the Rouché theorem.
Lemma 4.1 (Rouché theorem).
Suppose that  are entire functions of
are entire functions of  . If
. If  on a Jordan curve
on a Jordan curve  , then
, then  and
and  have the same number of zeros inside
have the same number of zeros inside  , counted multiplicities.
, counted multiplicities.
For later use, let us introduce the following elementary function:

Then  . Obviously,
. Obviously,  if and only if
if and only if  ,
,  . Define
. Define

where  is the circle in the
is the circle in the  -plane
-plane

Then  ,
,  , and
, and  for all
for all  . Let
. Let  be the unique solution of the following equation:
be the unique solution of the following equation:

Numerically,  . The following facts can be verified by elementary arguments.
. The following facts can be verified by elementary arguments.
Lemma 4.2.
One has

For the graph of  , see Figure 2.
, see Figure 2.
4.1. Large Eigenvalues
In the following we apply the Rouché theorem to study the spectrum  , that is, the zeros of the function
, that is, the zeros of the function  in the
in the  -plane. To this end, we consider problem
-plane. To this end, we consider problem  as a perturbation of the Dirichlet problem
as a perturbation of the Dirichlet problem  , whose eigenvalues are zeros of the function
, whose eigenvalues are zeros of the function

Let  . Equation (3.3) is the same as
. Equation (3.3) is the same as

which is considered as a perturbation of the following equation:

Due to the form of (4.7) and (4.8), one needs to only consider solutions in the right half-plane  of
of  . Notice that all solutions of (4.8) are
. Notice that all solutions of (4.8) are  ,
,  , which are simple zeros of
, which are simple zeros of  . For any
. For any  , we do not know whether all zeros of (4.7) are real. In order to overcome this, the proof is complicated than that in [11].
, we do not know whether all zeros of (4.7) are real. In order to overcome this, the proof is complicated than that in [11].
Let us derive another consequence from estimate (3.25) with some restriction on  . Suppose that
. Suppose that  satisfies
satisfies  . Define the positive function
. Define the positive function

where  is as in (3.14). Then
is as in (3.14). Then  is decreasing in
is decreasing in  .
.
Lemma 4.3.
Suppose that

Then for any  , where
, where  , one has
, one has

Proof.
We keep the notations in (3.23) Let  . If
. If  , it follows from (2.26) and (3.25) that
, it follows from (2.26) and (3.25) that

Using the function  in (4.9), we obtain
in (4.9), we obtain  . This proves (4.11).
. This proves (4.11).
Consider the following circles of the  -plane:
-plane:

Lemma 4.4.
Let  be as in (4.13). one has
be as in (4.13). one has

Proof.
Let  , where
, where  . Then
. Then  . By (2.26) we have
. By (2.26) we have

See (4.1) and (4.2). Notice that

By (2.25) and (4.15), we have

Since

Compared with (4.1) and (4.2), it follows from (3.13) that

Thus one has (4.14).
Proof of Theorem 1.3.
Let

where the constant  is as in Lemma 4.2. One has
is as in Lemma 4.2. One has  and
and  . Denote by
. Denote by  the disc enclosed by the circle
the disc enclosed by the circle  , that is,
, that is,

Since  ,
,  intersects
intersects  . See Figure 3.
. See Figure 3.
In the following, we always assume that  satisfies
satisfies

Suggested by (3.14), (4.9), and (4.11), we denote

Then, for all  as in (4.22), by (4.9) one has
as in (4.22), by (4.9) one has

Suppose that

Let us show that  must be positive. In fact, (4.25) implies that
must be positive. In fact, (4.25) implies that  . By result (4.11), we have
. By result (4.11), we have  . Hence
. Hence  is a zero of
is a zero of  inside some disc
inside some disc  . See Figure 3. W.l.o.g., let us assume that
. See Figure 3. W.l.o.g., let us assume that  . Then
. Then  satisfies
satisfies

For any  , one has
, one has

It follows from (4.5) that  . By (4.14), we have the estimate
. By (4.14), we have the estimate

Since (4.8) has the unique, simple zero  in
in  , by the Rouché theorem, we conclude from estimate (4.28) that (4.7) has the unique, simple zero
, by the Rouché theorem, we conclude from estimate (4.28) that (4.7) has the unique, simple zero  in
in  . Furthermore, denote that
. Furthermore, denote that

See (4.28). We have

Thus

Hence (4.7) has at least one real solution in the interval  . Due to the uniqueness, all eigenvalues
. Due to the uniqueness, all eigenvalues  as in (4.25) must be positive.
as in (4.25) must be positive.
Finally, it follows from Theorem 1.1 that  contains at most finitely many
contains at most finitely many  which do not satisfy (4.25). Thus the proof of Theorem 1.3 is completed.
which do not satisfy (4.25). Thus the proof of Theorem 1.3 is completed.
4.2. Small Eigenvalues
In order to prove Theorem 1.4, we need to show that all "small eigenvalues" are also real provided that  is small. The proof below is a modification of the proof of Theorem 1.3.
is small. The proof below is a modification of the proof of Theorem 1.3.
Proof of Theorem 1.4.
By (4.4), we can fix some  such that
such that


Denote that

In the following we assume that  satisfies (4.22), that is,
satisfies (4.22), that is,  . From the proof of Theorem 1.3,
. From the proof of Theorem 1.3,  consists of positive eigenvalues. See conditions (4.25) and (4.32). Moreover, for
consists of positive eigenvalues. See conditions (4.25) and (4.32). Moreover, for  , that is,
, that is,  , we obtain from estimate (4.14) and condition (4.33) that
, we obtain from estimate (4.14) and condition (4.33) that

Notice that equation

has (simple) solutions  ,
,  . By the Rouché theorem, we conclude that, if
. By the Rouché theorem, we conclude that, if  , the following problem:
, the following problem:

has precisely  solutions, counted multiplicity. Here
solutions, counted multiplicity. Here  has been written as
has been written as  to emphasize the dependence on
to emphasize the dependence on  .
.
Suppose that  . Equation (4.37) corresponds to the Dirichlet eigenvalue problem (1.1)–(1.4), which has only real eigenvalues. Moreover, all solutions of (4.37) are simple in this case [11]. Hence solutions of problem (4.37) can be denoted by
. Equation (4.37) corresponds to the Dirichlet eigenvalue problem (1.1)–(1.4), which has only real eigenvalues. Moreover, all solutions of (4.37) are simple in this case [11]. Hence solutions of problem (4.37) can be denoted by  ,
,  , where
, where

They are the first  eigenvalues of problem (1.1)–(1.4).
eigenvalues of problem (1.1)–(1.4).
In the following, we apply the implicit function theorem to prove that solutions of (4.37) inside  are actually real when
are actually real when  is small. Notice that
is small. Notice that  is a smooth real-valued function of
is a smooth real-valued function of  . By [11, page 21, Theorem
. By [11, page 21, Theorem  ], the derivative of
], the derivative of  w.r.t.
w.r.t.  is
is

In particular,

where

Since  is a Dirichlet eigenvalue of problem (1.1), we have
is a Dirichlet eigenvalue of problem (1.1), we have  . Moreover, the Liouville theorem for (1.1) implies that
. Moreover, the Liouville theorem for (1.1) implies that

In particular,  . Hence
. Hence

Now the implicit function theorem is applicable to (4.37). In conclusion, there exist some constant  and a continuously differentiable real-valued functions
and a continuously differentiable real-valued functions  of
of  such that
such that

Due to (4.38)–(4.44) and the continuity of  , one can assume that
, one can assume that

Thus  are different eigenvalues of
are different eigenvalues of  located in the interval
located in the interval  . Since (4.37) has precisely
. Since (4.37) has precisely  solutions inside
solutions inside  , we conclude that all solutions of (4.37) inside
, we conclude that all solutions of (4.37) inside  are necessarily real. Now we have proved that
are necessarily real. Now we have proved that  for all
for all  .
.
Notice that the constant  in (4.44) is constructed from the implicit function theorem. Generally speaking,
in (4.44) is constructed from the implicit function theorem. Generally speaking,  depends on
depends on  and all information of the potential
and all information of the potential  . However, during the application of the implicit function theorem to (4.37), the derivatives of
. However, during the application of the implicit function theorem to (4.37), the derivatives of  can be well controlled using estimates in [11], like (3.8)–(3.11). It is possible to choose some
can be well controlled using estimates in [11], like (3.8)–(3.11). It is possible to choose some  such that it depends on the norm
such that it depends on the norm  only. We will not give the detailed construction. Note that this has been already observed for large eigenvalues. For example,
only. We will not give the detailed construction. Note that this has been already observed for large eigenvalues. For example,  and
and  depend only on the norm
depend only on the norm  of
of  .
.
We end the paper with an open problem. Given  , for any
, for any  , due to Theorem 1.2, problem
, due to Theorem 1.2, problem  has always a sequence of real eigenvalues
has always a sequence of real eigenvalues  which tends to
which tends to  . In applications of eigenvalues to nonlinear problems, the smallest (real) eigenvalues
. In applications of eigenvalues to nonlinear problems, the smallest (real) eigenvalues  are of great importance. The main reason is that solutions of problem (1.1)–(1.2) are oscillatory only when
are of great importance. The main reason is that solutions of problem (1.1)–(1.2) are oscillatory only when  . As for the smallest eigenvalue of the Dirichlet problem (1.1)–(1.4), denoted by
. As for the smallest eigenvalue of the Dirichlet problem (1.1)–(1.4), denoted by  , one has the following variational characterization:
, one has the following variational characterization:

An open problem is what is the characterization like (4.46) for the smallest eigenvalue  of
of  . Once this is clear, some results on nonlinear problems in [5, 6, 8] can be extended by using eigenvalues of
. Once this is clear, some results on nonlinear problems in [5, 6, 8] can be extended by using eigenvalues of  .
.
Finally, let us remark that the approaches in this paper also can be applied to other multi-point boundary conditions like

or to more general Stieltjes boundary conditions [17]. In this sense, eigenvalue theory can be established for these nonsymmetric problems.
References
Anderson DR, Ma R:Second-order
 -point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.
-point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.Agarwal RP, Kiguradze I: On multi-point boundary value problems for linear ordinary differential equations with singularities. Journal of Mathematical Analysis and Applications 2004,297(1):131-151. 10.1016/j.jmaa.2004.05.002
Gupta CP, Ntouyas SK, Tsamatos PCh:On an
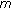 -point boundary-value problem for second-order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 1994,23(11):1427-1436. 10.1016/0362-546X(94)90137-6
-point boundary-value problem for second-order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 1994,23(11):1427-1436. 10.1016/0362-546X(94)90137-6Liu B, Yu J: Solvability of multi-point boundary value problems at resonance. I. Indian Journal of Pure and Applied Mathematics 2002,33(4):475-494.
Ma R:Nodal solutions for a second-order
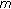 -point boundary value problem. Czechoslovak Mathematical Journal 2006,56(131)(4):1243-1263. 10.1007/s10587-006-0092-7
-point boundary value problem. Czechoslovak Mathematical Journal 2006,56(131)(4):1243-1263. 10.1007/s10587-006-0092-7Ma R, O'Regan D:Nodal solutions for second-order
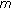 -point boundary value problems with nonlinearities across several eigenvalues. Nonlinear Analysis: Theory, Methods & Applications 2006,64(7):1562-1577. 10.1016/j.na.2005.07.007
-point boundary value problems with nonlinearities across several eigenvalues. Nonlinear Analysis: Theory, Methods & Applications 2006,64(7):1562-1577. 10.1016/j.na.2005.07.007Meng F, Du Z: Solvability of a second-order multi-point boundary value problem at resonance. Applied Mathematics and Computation 2009,208(1):23-30. 10.1016/j.amc.2008.11.026
Rynne BP:Spectral properties and nodal solutions for second-order,
 -point, boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(12):3318-3327. 10.1016/j.na.2006.10.014
-point, boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(12):3318-3327. 10.1016/j.na.2006.10.014Rynne BP: Second-order, three-point boundary value problems with jumping non-linearities. Nonlinear Analysis: Theory, Methods & Applications 2008,68(11):3294-3306. 10.1016/j.na.2007.03.023
Zhang M, Han Y: On the applications of Leray-Schauder continuation theorem to boundary value problems of semilinear differential equations. Annals of Differential Equations 1997,13(2):189-207.
Pöschel J, Trubowitz E: The Inverse Spectrum Theory. Academic Press, New York, NY, USA; 1987.
Zettl A: Sturm-Liouville Theory, Mathematical Surveys and Monographs. Volume 121. American Mathematical Society, Providence, RI, USA; 2005:xii+328.
Rynne BP:Spectral properties of second-order, multi-point,
 -Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2010,72(11):4244-4253. 10.1016/j.na.2010.01.054
-Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2010,72(11):4244-4253. 10.1016/j.na.2010.01.054Fink AM: Almost Periodic Differential Equations, Lecture Notes in Mathematics, Vol. 377. Springer, Berlin, Germany; 1974:viii+336.
Hale JK: Ordinary Differential Equations. 2nd edition. John Wiley & Sons, New York, NY, USA; 1969:xvi+332.
Meng G: Continuity of solutions and eigenvalues in measures with weak* topology, Ph.D. dissertation. Tsinghua University, Beijing, China; 2009.
García-Huidobro M, Manásevich R, Yan P, Zhang M:A
 -Laplacian problem with a multi-point boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(3):319-333.
-Laplacian problem with a multi-point boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(3):319-333.
Acknowledgments
The third author is supported by the Major State Basic Research Development Program (973 Program) of China (no. 2006CB805903), the Doctoral Fund of Ministry of Education of China (no. 20090002110079), the Program of Introducing Talents of Discipline to Universities (111 Program) of Ministry of Education and State Administration of Foreign Experts Affairs of China (2007), and the National Natural Science Foundation of China (no. 10531010). The authors would like to express their thanks to Ping Yan for her help during the preparation of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gao, J., Sun, D. & Zhang, M. Structure of Eigenvalues of Multi-Point Boundary Value Problems. Adv Differ Equ 2010, 381932 (2010). https://doi.org/10.1155/2010/381932
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/381932
 , one has
, one has 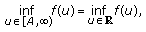
 is non-zero and
is non-zero and 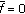 . Then
. Then 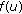 is oscillatory as
is oscillatory as  , that is,
, that is, 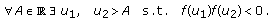
 , choose
, choose  such that
such that 
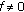 and
and 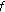 has mean value
has mean value  , it is easy to see that
, it is easy to see that 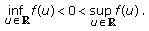

 and its positive zeros, where
and its positive zeros, where  ,
,  and
and  .
.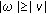 , it follows from the uniform limits in (3.4) that
, it follows from the uniform limits in (3.4) that 


 .
.
 in the
in the
 -plane.
-plane.
 -point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.
-point eigenvalue problems on time scales. Advances in Difference Equations 2006, 2006:-17.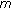 -point boundary-value problem for second-order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 1994,23(11):1427-1436. 10.1016/0362-546X(94)90137-6
-point boundary-value problem for second-order ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 1994,23(11):1427-1436. 10.1016/0362-546X(94)90137-6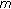 -point boundary value problem. Czechoslovak Mathematical Journal 2006,56(131)(4):1243-1263. 10.1007/s10587-006-0092-7
-point boundary value problem. Czechoslovak Mathematical Journal 2006,56(131)(4):1243-1263. 10.1007/s10587-006-0092-7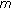 -point boundary value problems with nonlinearities across several eigenvalues. Nonlinear Analysis: Theory, Methods & Applications 2006,64(7):1562-1577. 10.1016/j.na.2005.07.007
-point boundary value problems with nonlinearities across several eigenvalues. Nonlinear Analysis: Theory, Methods & Applications 2006,64(7):1562-1577. 10.1016/j.na.2005.07.007 -point, boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(12):3318-3327. 10.1016/j.na.2006.10.014
-point, boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2007,67(12):3318-3327. 10.1016/j.na.2006.10.014 -Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2010,72(11):4244-4253. 10.1016/j.na.2010.01.054
-Laplacian boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2010,72(11):4244-4253. 10.1016/j.na.2010.01.054 -Laplacian problem with a multi-point boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(3):319-333.
-Laplacian problem with a multi-point boundary condition. Nonlinear Analysis: Theory, Methods & Applications 2004,59(3):319-333.