- Research Article
- Open access
- Published:
Stability of a Jensen Type Logarithmic Functional Equation on Restricted Domains and Its Asymptotic Behaviors
Advances in Difference Equations volume 2010, Article number: 432796 (2010)
Abstract
Let  be the set of positive real numbers,
be the set of positive real numbers,  a Banach space,
a Banach space,  and
and  ,
,  with
with  . We prove the Hyers-Ulam stability of the Jensen type logarithmic functional inequality
. We prove the Hyers-Ulam stability of the Jensen type logarithmic functional inequality  in restricted domains of the form
in restricted domains of the form  for fixed
for fixed  with
with  or
or  and
and  . As consequences of the results we obtain asymptotic behaviors of the inequality as
. As consequences of the results we obtain asymptotic behaviors of the inequality as  .
.
1. Introduction
The stability problems of functional equations have been originated by Ulam in 1940 (see [1]). One of the first assertions to be obtained is the following result, essentially due to Hyers [2], that gives an answer for the question of Ulam.
Theorem 1.1.
Suppose that  is an additive semigroup,
is an additive semigroup,  is a Banach space,
is a Banach space,  , and
, and  satisfies the inequality
satisfies the inequality

for all  . Then there exists a unique function
. Then there exists a unique function  satisfying
satisfying

for which

for all  .
.
In 1950-1951 this result was generalized by the authors Aoki [3] and Bourgin [4, 5]. Unfortunately, no results appeared until 1978 when Th. M. Rassias generalized the Hyers' result to a new approximately linear mappings [6]. Following the Rassias' result, a great number of the papers on the subject have been published concerning numerous functional equations in various directions [6–16]. For more precise descriptions of the Hyers-Ulam stability and related results, we refer the reader to the paper of Moszner [17]. Among the results, the stability problem in a restricted domain was investigated by Skof, who proved the stability problem of the inequality (1.1) in a restricted domain [16]. Developing this result, Jung considered the stability problems in restricted domains for the Jensen functional equation [11] and Jensen type functional equations [14]. The results can be summarized as follows: let  and
and  be a real normed space and a real Banach space, respectively. For fixed
be a real normed space and a real Banach space, respectively. For fixed  , if
, if  satisfies the functional inequalities (such as that of Cauchy, Jensen and Jensen type, etc.) for all
satisfies the functional inequalities (such as that of Cauchy, Jensen and Jensen type, etc.) for all  with
with  , the inequalities hold for all
, the inequalities hold for all  . We also refer the reader to [18–26] for some interesting results on functional equations and their Hyers-Ulam stabilities in restricted conditions.
. We also refer the reader to [18–26] for some interesting results on functional equations and their Hyers-Ulam stabilities in restricted conditions.
Throughout this paper, we denote by  the set of positive real numbers,
the set of positive real numbers,  a Banach space,
a Banach space,  , and
, and  with
with  . We prove the Hyers-Ulam stability of the Jensen type logarithmic functional inequality
. We prove the Hyers-Ulam stability of the Jensen type logarithmic functional inequality

in the restricted domains of the form  for fixed
for fixed  with
with  or
or  , and
, and  . As a result, we prove that if the inequality (1.4) holds for all
. As a result, we prove that if the inequality (1.4) holds for all  , there exists a unique function
, there exists a unique function  satisfying
satisfying

for which

for all  if
if  ,
,

for all  if
if  , and
, and

for all  if
if  . As a consequence of the result we obtain the stability of the inequality
. As a consequence of the result we obtain the stability of the inequality

in the restricted domains of the form  for fixed
for fixed  with
with  or
or  , and
, and  . Also we obtain asymptotic behaviors of the inequalities (1.4) and (1.9) as
. Also we obtain asymptotic behaviors of the inequalities (1.4) and (1.9) as  and
and  , respectively.
, respectively.
2. Hyers-Ulam Stability in Restricted Domains
We call the functions satisfying (1.5)logarithmic functions. As a direct consequence of Theorem 1.1, we obtain the stability of the logarithmic functional equation, viewing  as a multiplicative group (see also the result of Forti [9]).
as a multiplicative group (see also the result of Forti [9]).
Theorem A.
Suppose that  ,
,  , and
, and

for all  . Then there exists a unique logarithmic function
. Then there exists a unique logarithmic function  satisfying
satisfying

for all  .
.
We first consider the usual logarithmic functional inequality (2.1) in the restricted domains  .
.
Theorem 2.1.
Let  ,
,  with
with  or
or  . Suppose that
. Suppose that  satisfies
satisfies

for all  , with
, with  . Then there exists a unique logarithmic function
. Then there exists a unique logarithmic function  such that
such that

for all  .
.
Proof.
From the symmetry of the inequality we may assume that  . For given
. For given  , choose a
, choose a  such that
such that  ,
,  , and
, and  . Then we have
. Then we have

This completes the proof.
Now we consider the Hyers-Ulam stability of the Jensen type logarithmic functional inequality (1.4) in the restricted domains  .
.
Theorem 2.2.
Let  . Suppose that
. Suppose that  satisfies
satisfies

for all  , with
, with  . Then there exists a unique logarithmic function
. Then there exists a unique logarithmic function  such that
such that

for all  .
.
Proof.
Replacing  by
by  ,
,  by
by  in (2.6) we have
in (2.6) we have

for all  , with
, with  .
.
For given  , choose a
, choose a  such that
such that  ,
,  ,
,  , and
, and  . Replacing
. Replacing  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  in (2.8) we have
in (2.8) we have

Now by Theorem A, there exists a unique logarithmic function  such that
such that

for all  . This completes the proof.
. This completes the proof.
As a matter of fact, we obtain that  in Theorem 2.2 provided that
in Theorem 2.2 provided that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number.
is a rational number.
Theorem 2.3.
Let  ,
,  ,
,  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies
satisfies

for all  , with
, with  . Then one has
. Then one has

for all  .
.
Proof.
We prove (2.12) only for the case that  and
and  or
or  is a rational number since the other case is similarly proved. From (2.7) and (2.11), using the triangle inequality we have
is a rational number since the other case is similarly proved. From (2.7) and (2.11), using the triangle inequality we have

for all  , with
, with  , where
, where  . If
. If  , putting
, putting  in (2.13) we have
in (2.13) we have

for all  , with
, with  . It is easy to see that
. It is easy to see that  for all
for all  and all rational numbers
and all rational numbers  . Thus if
. Thus if  is a rational number, it follows from (2.14) that
is a rational number, it follows from (2.14) that

for all  , with
, with  . If there exists
. If there exists  such that
such that  , we can choose a rational number
, we can choose a rational number  such that
such that  and
and  (it is realized when
(it is realized when  is large if
is large if  , and when
, and when  is large if
is large if  ). Now we have
). Now we have

Thus it follows that  . If
. If  is a rational number, it follows from (2.14) that
is a rational number, it follows from (2.14) that

for all  , with
, with  , which implies
, which implies

for all  , with
, with  . Similarly, using (2.18) we can show that
. Similarly, using (2.18) we can show that  . If
. If  , choosing
, choosing  such that
such that  , putting
, putting  in (2.13) and using the triangle inequality we have
in (2.13) and using the triangle inequality we have

for all  . Similarly, using (2.19) we can show that
. Similarly, using (2.19) we can show that  . Thus the inequality (2.12) follows from (2.7). This completes the proof.
. Thus the inequality (2.12) follows from (2.7). This completes the proof.
Theorem 2.4.
Let 
 with
with  or
or  . Suppose that
. Suppose that  satisfies
satisfies

for all  , with
, with  . Then there exists a unique logarithmic function
. Then there exists a unique logarithmic function  such that
such that

for all  if
if  , and
, and

for all  if
if  .
.
Proof.
Assume that  . For given
. For given  , choose a
, choose a  such that
such that  ,
,  ,
,  and
and  . Replacing
. Replacing  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by 1,
by 1,  by
by  in (2.20) we have
in (2.20) we have

Dividing (2.23) by  and using Theorem A, we obtain that there exists a unique logarithmic function
and using Theorem A, we obtain that there exists a unique logarithmic function  such that
such that

for all  . Assume that
. Assume that  . For given
. For given  , choose a
, choose a  such that
such that  and
and  . Replacing
. Replacing  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by
by  ,
,  by
by  ;
;  by 1,
by 1,  by
by  in (2.20) we have
in (2.20) we have

Dividing (2.25) by  and using Theorem A, we obtain that there exists a unique logarithmic function
and using Theorem A, we obtain that there exists a unique logarithmic function  such that
such that

for all  . This completes the proof.
. This completes the proof.
From Theorem 2.4, using the same approach as in the proof of Theorem 2.3 we have the following.
Theorem 2.5.
Let  ,
,  with
with  or
or  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies
satisfies

for all  , with
, with  . Then one has
. Then one has

for all  if
if  , and
, and

for all  if
if  .
.
We call  an additive function provided that
an additive function provided that

for all  . Using Theorem 2.2 we have the following.
. Using Theorem 2.2 we have the following.
Corollary 2.6 (see [22]).
Let  ,
,  with
with  . Suppose that
. Suppose that  satisfies
satisfies

for all  , with
, with  . Then there exists a unique additive function
. Then there exists a unique additive function  such that
such that

for all  .
.
Proof.
Replacing  by
by  ,
,  by
by  in (2.31) and setting
in (2.31) and setting  we have
we have

for all  , with
, with  . Using Theorem 2.2, we have
. Using Theorem 2.2, we have

for all  , which implies
, which implies

for all  . Letting
. Letting  we get the result.
we get the result.
Using Theorem 2.3, we have the following.
Corollary 2.7.
Let  ,
,  with
with  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies
satisfies

for all  , with
, with  . Then one has
. Then one has

for all  .
.
Using Theorem 2.4, we have the following.
Corollary 2.8.
Let  ,
,  with
with  or
or  . Suppose that
. Suppose that  satisfies
satisfies

for all  , with
, with  . Then there exists a unique additive function
. Then there exists a unique additive function  such that
such that

for all  if
if  , and
, and

for all  if
if  .
.
Using Theorem 2.5, we have the following.
Corollary 2.9.
Let  ,
,  with
with  or
or  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies
satisfies

for all  , with
, with  . Then one has
. Then one has

for all  if
if  , and
, and

for all  if
if  .
.
3. Asymptotic Behavior of the Inequality
In this section, we consider asymptotic behaviors of the inequalities (1.4) and (2.1).
Theorem 3.1.
Let  satisfy one of the conditions;
satisfy one of the conditions;  ,
,  . Suppose that
. Suppose that  satisfies the asymptotic condition
satisfies the asymptotic condition

as  . Then
. Then  is a logarithmic function.
is a logarithmic function.
Proof.
By the condition (3.1), for each  , there exists
, there exists  such that
such that

for all  , with
, with  . By Theorem 2.1, there exists a unique logarithmic function
. By Theorem 2.1, there exists a unique logarithmic function  such that
such that

for all  . From (3.4) we have
. From (3.4) we have

for all  and all positive integers
and all positive integers  . Now, the inequality (3.4) implies
. Now, the inequality (3.4) implies  . Indeed, for all
. Indeed, for all  and rational numbers
and rational numbers  we have
we have

Letting  in (3.5), we have
in (3.5), we have  . Thus, letting
. Thus, letting  in (3.3), we get the result.
in (3.3), we get the result.
Theorem 3.2.
Let  satisfy one of the conditions;
satisfy one of the conditions;  ,
,  ,
,  . Suppose that
. Suppose that  satisfies the asymptotic condition
satisfies the asymptotic condition

as  . Then there exists a unique logarithmic function
. Then there exists a unique logarithmic function  such that
such that

for all  .
.
Proof.
By the condition (3.6), for each  , there exists
, there exists  such that
such that

for all  , with
, with  . By Theorems 2.2 and 2.4, there exists a unique logarithmic function
. By Theorems 2.2 and 2.4, there exists a unique logarithmic function  such that
such that

if  ,
,

if  , and
, and

if  . For all cases (3.9), (3.10), and (3.11), there exists
. For all cases (3.9), (3.10), and (3.11), there exists  such that
such that

for all  and all positive integers
and all positive integers  . Now as in the proof of Theorem 3.1, it follows from (3.12) that
. Now as in the proof of Theorem 3.1, it follows from (3.12) that  for all
for all  . Letting
. Letting  in (3.9), (3.10), and (3.11) we get the result.
in (3.9), (3.10), and (3.11) we get the result.
Similarly using Theorems 2.3 and 2.5, we have the following.
Theorem 3.3.
Let  satisfy one of the conditions;
satisfy one of the conditions;  ,
,  ,
,  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies the asymptotic condition
satisfies the asymptotic condition

as  . Then
. Then  is a constant function.
is a constant function.
Using Corollaries 2.6 and 2.8 we have the following.
Corollary 3.4.
Let  ,
,  satisfy one of the conditions
satisfy one of the conditions  ,
,  , or
, or  . Suppose that
. Suppose that  satisfies
satisfies

as  . Then there exists a unique additive function
. Then there exists a unique additive function  such that
such that

for all  .
.
Using Corollaries 2.7 and 2.9 we have the following.
Corollary 3.5.
Let  ,
,  satisfy one of the conditions
satisfy one of the conditions  ,
,  , or
, or  . Suppose that
. Suppose that  and
and  or
or  is a rational number, or
is a rational number, or  and
and  or
or  is a rational number, and
is a rational number, and  satisfies
satisfies

as  . Then
. Then  is a constant function.
is a constant function.
References
Ulam SM: A Collection of Mathematical Problems. Interscience, New York, NY, USA; 1960.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Bourgin DG: Multiplicative transformations. Proceedings of the National Academy of Sciences of the United States of America 1950, 36: 564–570. 10.1073/pnas.36.10.564
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Rassias TM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Chung J: A distributional version of functional equations and their stabilities. Nonlinear Analysis: Theory, Methods & Applications 2005,62(6):1037–1051. 10.1016/j.na.2005.04.016
Chung J: Stability of approximately quadratic Schwartz distributions. Nonlinear Analysis: Theory, Methods & Applications 2007,67(1):175–186. 10.1016/j.na.2006.05.005
Forti GL: The stability of homomorphisms and amenability, with applications to functional equations. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1987, 57: 215–226. 10.1007/BF02941612
Hyers DH, Isac G, Rassias TM: Stability of Functional Equations in Several Variables, Progress in Nonlinear Differential Equations and their Applications. Volume 34. Birkhäuser, Boston, Mass, USA; 1998:vi+313.
Jung S-M: Hyers-Ulam-Rassias stability of Jensen's equation and its application. Proceedings of the American Mathematical Society 1998,126(11):3137–3143. 10.1090/S0002-9939-98-04680-2
Jun K-W, Kim H-M: Stability problem for Jensen-type functional equations of cubic mappings. Acta Mathematica Sinica 2006,22(6):1781–1788. 10.1007/s10114-005-0736-9
Kim GH, Lee YW: Boundedness of approximate trigonometric functional equations. Applied Mathematics Letters 2009,31(4):439–443. 10.1016/j.aml.2008.06.013
Rassias JM: On the Ulam stability of mixed type mappings on restricted domains. Journal of Mathematical Analysis and Applications 2002,276(2):747–762. 10.1016/S0022-247X(02)00439-0
Rassias JM, Rassias MJ: On the Ulam stability of Jensen and Jensen type mappings on restricted domains. Journal of Mathematical Analysis and Applications 2003,281(2):516–524. 10.1016/S0022-247X(03)00136-7
Skof F: Sull'approssimazione delle applicazioni localmente
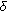 -additive. Atti della Reale Accademia delle Scienze di Torino. Classe di Scienze Fisiche, Matematiche e Naturali 1983, 117: 377–389.
-additive. Atti della Reale Accademia delle Scienze di Torino. Classe di Scienze Fisiche, Matematiche e Naturali 1983, 117: 377–389.Moszner Z: On the stability of functional equations. Aequationes Mathematicae 2009,77(1–2):33–88. 10.1007/s00010-008-2945-7
Batko B: Stability of an alternative functional equation. Journal of Mathematical Analysis and Applications 2008,339(1):303–311. 10.1016/j.jmaa.2007.07.001
Batko B: On approximation of approximate solutions of Dhombres' equation. Journal of Mathematical Analysis and Applications 2008,340(1):424–432. 10.1016/j.jmaa.2007.08.009
Brzdęk J: On the quotient stability of a family of functional equations. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4396–4404. 10.1016/j.na.2009.02.123
Brzdęk J: On a method of proving the Hyers-Ulam stability of functional equations on restricted domains. The Australian Journal of Mathematical Analysis and Applications 2009,6(1):1–10.
Brzdęk J: On stability of a family of functional equations. Acta Mathematica Hungarica 2010,128(1–2):139–149. 10.1007/s10474-010-9169-8
Brzdęk J, Sikorska J: A conditional exponential functional equation and its stability. Nonlinear Analysis: Theory, Methods & Applications 2010,72(6):2923–2934. 10.1016/j.na.2009.11.036
Sikorska J: On two conditional Pexider functional equations and their stabilities. Nonlinear Analysis: Theory, Methods & Applications 2009,70(7):2673–2684. 10.1016/j.na.2008.03.054
Sikorska J: On a Pexiderized conditional exponential functional equation. Acta Mathematica Hungarica 2009,125(3):287–299. 10.1007/s10474-009-9019-8
Sikorska J: Exponential functional equation on spheres. Applied Mathematics Letters 2010,23(2):156–160. 10.1016/j.aml.2009.09.004
Acknowledgments
The author expresses his sincere gratitude to a referee of the paper for many useful comments and introducing the interesting related recent results including the papers [17–26]. This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (MEST) (no. 2010-0016963).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chung, JY. Stability of a Jensen Type Logarithmic Functional Equation on Restricted Domains and Its Asymptotic Behaviors. Adv Differ Equ 2010, 432796 (2010). https://doi.org/10.1155/2010/432796
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/432796
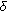 -additive. Atti della Reale Accademia delle Scienze di Torino. Classe di Scienze Fisiche, Matematiche e Naturali 1983, 117: 377–389.
-additive. Atti della Reale Accademia delle Scienze di Torino. Classe di Scienze Fisiche, Matematiche e Naturali 1983, 117: 377–389.