- Research Article
- Open access
- Published:
Existence and Nonexistence of Global Solutions of the Quasilinear Parabolic Equations with Inhomogeneous Terms
Advances in Difference Equations volume 2010, Article number: 451619 (2010)
Abstract
We consider the quasilinear parabolic equation with inhomogeneous term  ,
,  , where
, where  ,
,  ,
,  ,
,  , and
, and  ,
,  . In this paper, we investigate the critical exponents of this equation.
. In this paper, we investigate the critical exponents of this equation.
1. Introduction
We consider the quasi-linear parabolic equation with inhomogeneous term

where  ,
,  ,
,  ,
,  , and
, and  .
.
For the solution  of (1.1), let
of (1.1), let  be the maximal existence time, that is,
be the maximal existence time, that is,

If  , we say that
, we say that  is a global solution; if
is a global solution; if  , we say that
, we say that  blows up in finite time.
blows up in finite time.
For quasi-linear parabolic equations, the authors of [1–5] and so on. study the homogeneous equations (i.e.,  in (1.1)). Baras and Kersner [1] proved that (1.1) with
in (1.1)). Baras and Kersner [1] proved that (1.1) with  and
and  has a global solution, two constants
has a global solution, two constants  and
and  depending on
depending on  and
and  exist such that
exist such that

Mochizuki and Mukai [2] and Qi [4] study the case  ,
,  , Pinsky [3] studies the case
, Pinsky [3] studies the case  ,
,  , and Suzuki [5] studies the case
, and Suzuki [5] studies the case  ,
,  . The following two results are proved by them:
. The following two results are proved by them:
-
(1)
if
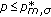 , then every nontrivial solution
, then every nontrivial solution  of (1.1) blows up in finite time;
of (1.1) blows up in finite time; -
(2)
if
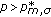 , then (1.1) has a global solution for some initial value
, then (1.1) has a global solution for some initial value 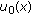 ,
,
where  for
for  ,
,  and for
and for  ,
,  ,
,  for
for  ,
,  . This
. This  is called the critical exponent.
is called the critical exponent.
On the other hand, [6–9] and so on. study the inhomogeneous equations (i.e.,  in (1.1)). Bandle et al. [6] study the case
in (1.1)). Bandle et al. [6] study the case  ,
,  , and Zeng [8] and Zhang [9] study the case
, and Zeng [8] and Zhang [9] study the case  . In this paper, we investigate the critical exponents of (1.1) in the case
. In this paper, we investigate the critical exponents of (1.1) in the case  . Our results are as follows.
. Our results are as follows.
Theorem 1.1.
Suppose that  ,
,  ,
,  , and
, and  . Put
. Put

-
(a)
If
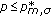 , then every nontrivial solution
, then every nontrivial solution 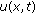 of (1.1) blows up in finite time.
of (1.1) blows up in finite time. -
(b)
If
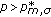 ,
,  , and
, and  , then (1.1) has a global solution for some constants
, then (1.1) has a global solution for some constants 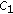 and
and 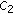 .
.
Theorem 1.2.
Suppose that  ,
,  ,
,  , and
, and  . Then every nontrivial solution
. Then every nontrivial solution  of (1.1) blows up in finite time.
of (1.1) blows up in finite time.
Remark 1.3.
Theorems 1.1 and 1.2 are the extension of the results of [8]. If we put  in these theorems, the same results as Theorem 1 in [8] are obtained.
in these theorems, the same results as Theorem 1 in [8] are obtained.
We will prove Theorem 1.1(a) and (b) in Sections 3 and 4, respectively. The proof of Theorem 1.2 is included in the proof of Theorem 1.1(a).
In the following,  and
and  are two given positive real numbers greater than 1.
are two given positive real numbers greater than 1.  is a positive constant independent of
is a positive constant independent of  and
and  , and its value may change from line to line.
, and its value may change from line to line.
2. Preliminaries
In this section, we first give the definition of a solution for Problem (1.1) and then cite the comparison theorem and a known result.
Definition 2.1.
A continuous function  is called a solution of Problem (1.1) in
is called a solution of Problem (1.1) in  if the following holds:
if the following holds:
-
(i)
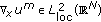 ;
; -
(ii)
for any bounded domain
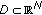 and for all
and for all  and vanishing on
and vanishing on 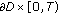 ,
,

for all  .
.
Lemma 2.2 (the comparison theorem).
Let  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  ;
;  , and satisfy
, and satisfy

Then  for all
for all  , where
, where  is a bounded domain in
is a bounded domain in  with smooth boundary
with smooth boundary  or
or  and
and  .
.
Lemma 2.3 (the monotonicity property).
Let  be a nonnegative sub-solution to the stationary problems of Problem (1.1). Then the positive solution
be a nonnegative sub-solution to the stationary problems of Problem (1.1). Then the positive solution  with initial data
with initial data  is monotone increasing to
is monotone increasing to  .
.
3. Proof of Theorem 1.1(a)
We first consider the following problem:

It is clear that the positive solution of Problem (3.1) is a sub-solution of Problem (1.1). If every positive solution of Problem (3.1) blows up in finite time, then, by Lemma 2.2, every positive solution of Problem (1.1) also blows up in finite time. Therefore, we only need to consider Problem (3.1).
The stationary problem of Problem (3.1) is as follows:

It is obvious that 0 is a sub-solution of Problem (3.2) and does not satisfy Problem (3.2). Thus, by making use of Lemmas 2.2 and 2.3, the positive solution of Problem (3.1) is monotone increasing to  .
.
We argue by contradiction. Assume that Problem (3.1) has a global positive solution for  .
.
Let  and
and  be two functions in
be two functions in  , and satisfy
, and satisfy
-
(i)
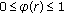 in
in  ;
; 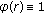 in
in  ,
, 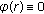 in
in 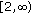 ;
; 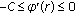 ,
,  ;
; -
(ii)
 in
in 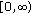 ;
; 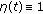 in
in 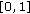 ,
, 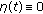 in
in 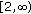 ;
; 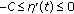 .
.
For  and
and  , define
, define  , and let
, and let  be a cut-off function, where
be a cut-off function, where  ,
,  . It is easy to check that
. It is easy to check that

Let

where  is a positive number to be determined. Then
is a positive number to be determined. Then

Since  , there exist
, there exist  and
and  such that
such that  for
for  :
:

Hence, by the definition of  and
and  , we have
, we have

Since  and
and

we obtain from (3.3) that

in  and
and

in  . Thus, (3.7) becomes
. Thus, (3.7) becomes

Let  be large enough such that
be large enough such that  and
and  , and let
, and let  be as follows:
be as follows:

Then, by making use of Young's inequality, we have

where  and
and

where  ,
,  . Thus, (3.11) becomes
. Thus, (3.11) becomes

For  , since
, since  ,
,  , and
, and  , we have
, we have

For  , since
, since  ,
,  , and
, and  , we have
, we have

For  , since
, since  , and
, and  , we have
, we have

Let  such that
such that  , then
, then

that is,

Thus

By the integral mean value theorem, there exists  such that
such that

that is,

Since  is a large positive number and a random selection, and
is a large positive number and a random selection, and  is monotone increasing to
is monotone increasing to  , there exists a positive number
, there exists a positive number  for any fixed
for any fixed  such that, for all
such that, for all  ,
,

By the monotone increasing property of  ,
,  also is increasing to
also is increasing to  . This, combined with (3.24), yields that the limit
. This, combined with (3.24), yields that the limit  exists such that
exists such that

Since  is nonnegative,
is nonnegative,  is monotone increasing to
is monotone increasing to  . This, combined with (3.25), yields that
. This, combined with (3.25), yields that  exists. Thus, for any small
exists. Thus, for any small  , there exists a large positive constant which still is denoted by
, there exists a large positive constant which still is denoted by  , such that, for
, such that, for  ,
,

Hence, by similar argument as that in (3.24), there exists a large positive number  such that
such that

On the other hand, we argue as in [6, 10]. Let  be a positive function satisfying.
be a positive function satisfying.
-
(i)
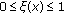 in
in 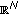 ;
; 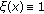 in
in 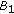 ,
, 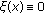 in
in 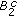 ;
; -
(ii)
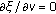 on
on  ;
; -
(iii)
for any
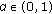 , there exists a positive constant
, there exists a positive constant 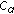 such that
such that  .
.
Let  and
and  be as defined in (3.26) and (3.27). Multiplying (3.1) by
be as defined in (3.26) and (3.27). Multiplying (3.1) by  and then integrating by parts in
and then integrating by parts in  , we have
, we have

By the definition of  , Hölder's inequality, and (3.27), we have
, Hölder's inequality, and (3.27), we have

where  ,
,  , since
, since

Let  and
and  . Then, by making use of (3.29) and
. Then, by making use of (3.29) and  for
for  , (3.28) becomes
, (3.28) becomes

Thus, let  be small enough such that
be small enough such that  , then
, then  .
.
Let  . By making use of Hölder's inequality, we obtain that
. By making use of Hölder's inequality, we obtain that

where  . Thus, we obtain that
. Thus, we obtain that

Since  for all
for all  , we have
, we have

Let  , then
, then

Let  such that
such that  . Since
. Since  , by solving the differential inequality (3.35) in
, by solving the differential inequality (3.35) in  , we have
, we have

Thus, there exists  with
with  , such that
, such that  , which implies that
, which implies that  and then
and then  blow up in finite time. It contradicts our assumption. Therefore, every positive solution of Problem (3.1) blows up in finite time. Hence, every positive solution of Problem (1.1) blows up in finite time.
blow up in finite time. It contradicts our assumption. Therefore, every positive solution of Problem (3.1) blows up in finite time. Hence, every positive solution of Problem (1.1) blows up in finite time.
4. Proof of Theorem 1.1(b)
In this section, we prove that for  , there exist some
, there exist some  and
and  , such that Problem (1.1) admits a global positive solution.
, such that Problem (1.1) admits a global positive solution.
We first consider the stationary problem of Problem (1.1) as follows:

Let  , where
, where  and the positive constant
and the positive constant  satisfies
satisfies

Then, we have

Since  and
and  , we have
, we have

where  . Thus, if
. Thus, if  and
and  , then
, then  is a supersolution of Problem (1.1). It is obvious that
is a supersolution of Problem (1.1). It is obvious that  is s sub-solution of Problem (1.1). Therefore, by the iterative process and the comparison theorem, Problem (1.1) admits a global positive solution.
is s sub-solution of Problem (1.1). Therefore, by the iterative process and the comparison theorem, Problem (1.1) admits a global positive solution.
References
Baras P, Kersner R: Local and global solvability of a class of semilinear parabolic equations. Journal of Differential Equations 1987,68(2):238-252. 10.1016/0022-0396(87)90194-X
Mochizuki K, Mukai K: Existence and nonexistence of global solutions to fast diffusions with source. Methods and Applications of Analysis 1995,2(1):92-102.
Pinsky RG: Existence and nonexistence of global solutions for
 in
in 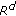 . Journal of Differential Equations 1997,133(1):152-177. 10.1006/jdeq.1996.3196
. Journal of Differential Equations 1997,133(1):152-177. 10.1006/jdeq.1996.3196Qi Y-W:On the equation
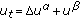 . Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1993,123(2):373-390. 10.1017/S0308210500025750
. Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1993,123(2):373-390. 10.1017/S0308210500025750Suzuki R: Existence and nonexistence of global solutions of quasilinear parabolic equations. Journal of the Mathematical Society of Japan 2002,54(4):747-792. 10.2969/jmsj/1191591992
Bandle C, Levine HA, Zhang QS: Critical exponents of Fujita type for inhomogeneous parabolic equations and systems. Journal of Mathematical Analysis and Applications 2000,251(2):624-648. 10.1006/jmaa.2000.7035
Kirane M, Qafsaoui M: Global nonexistence for the Cauchy problem of some nonlinear reaction-diffusion systems. Journal of Mathematical Analysis and Applications 2002,268(1):217-243. 10.1006/jmaa.2001.7819
Zeng X: The critical exponents for the quasi-linear parabolic equations with inhomogeneous terms. Journal of Mathematical Analysis and Applications 2007,332(2):1408-1424. 10.1016/j.jmaa.2006.11.034
Zhang QS: Blow-up results for nonlinear parabolic equations on manifolds. Duke Mathematical Journal 1999,97(3):515-539. 10.1215/S0012-7094-99-09719-3
Qi Y-W:The critical exponents of parabolic equations and blow-up in
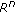 . Proceedings of the Royal Society of Edinburgh. Section A 1998,128(1):123-136. 10.1017/S0308210500027190
. Proceedings of the Royal Society of Edinburgh. Section A 1998,128(1):123-136. 10.1017/S0308210500027190
Acknowledgments
This paper was introduced to the author by Professor Kiyoshi Mochizuki in Chuo University. The author would like to thank him for his proper guidance. The author would also like to thank Ryuichi Suzuki for useful discussions and friendly encouragement during the preparation of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kobayashi, Y. Existence and Nonexistence of Global Solutions of the Quasilinear Parabolic Equations with Inhomogeneous Terms. Adv Differ Equ 2010, 451619 (2010). https://doi.org/10.1155/2010/451619
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/451619
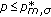 , then every nontrivial solution
, then every nontrivial solution  of (1.1) blows up in finite time;
of (1.1) blows up in finite time;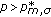 , then (1.1) has a global solution for some initial value
, then (1.1) has a global solution for some initial value 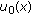 ,
,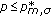 , then every nontrivial solution
, then every nontrivial solution 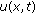 of (1.1) blows up in finite time.
of (1.1) blows up in finite time.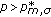 ,
,  , and
, and  , then (1.1) has a global solution for some constants
, then (1.1) has a global solution for some constants 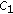 and
and 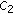 .
.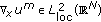 ;
;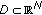 and for all
and for all  and vanishing on
and vanishing on 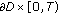 ,
,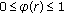 in
in  ;
; 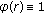 in
in  ,
, 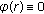 in
in 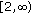 ;
; 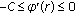 ,
,  ;
; in
in 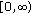 ;
; 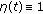 in
in 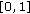 ,
, 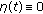 in
in 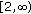 ;
; 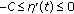 .
.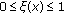 in
in 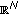 ;
; 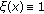 in
in 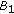 ,
, 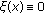 in
in 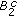 ;
;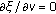 on
on  ;
;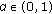 , there exists a positive constant
, there exists a positive constant 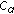 such that
such that  .
. in
in 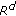 . Journal of Differential Equations 1997,133(1):152-177. 10.1006/jdeq.1996.3196
. Journal of Differential Equations 1997,133(1):152-177. 10.1006/jdeq.1996.3196 . Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1993,123(2):373-390. 10.1017/S0308210500025750
. Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 1993,123(2):373-390. 10.1017/S0308210500025750 . Proceedings of the Royal Society of Edinburgh. Section A 1998,128(1):123-136. 10.1017/S0308210500027190
. Proceedings of the Royal Society of Edinburgh. Section A 1998,128(1):123-136. 10.1017/S0308210500027190