- Research Article
- Open access
- Published:
A Discrete Equivalent of the Logistic Equation
Advances in Difference Equations volume 2010, Article number: 457073 (2010)
Abstract
A discrete equivalent and not analogue of the well-known logistic differential equation is proposed. This discrete equivalent logistic equation is of the Volterra convolution type, is obtained by use of a functional-analytic method, and is explicitly solved using the  -transform method. The connection of the solution of the discrete equivalent logistic equation with the solution of the logistic differential equation is discussed. Also, some differences of the discrete equivalent logistic equation and the well-known discrete analogue of the logistic equation are mentioned. It is hoped that this discrete equivalent of the logistic equation could be a better choice for the modelling of various problems, where different versions of known discrete logistic equations are used until nowadays.
-transform method. The connection of the solution of the discrete equivalent logistic equation with the solution of the logistic differential equation is discussed. Also, some differences of the discrete equivalent logistic equation and the well-known discrete analogue of the logistic equation are mentioned. It is hoped that this discrete equivalent of the logistic equation could be a better choice for the modelling of various problems, where different versions of known discrete logistic equations are used until nowadays.
1. Introduction
The well-known logistic differential equation was originally proposed by the Belgian mathematician Pierre-François Verhulst (1804–1849) in 1838, in order to describe the growth of a population  under the assumptions that the rate of growth of the population was proportional to
under the assumptions that the rate of growth of the population was proportional to
the existing population and
the amount of available resources.
When this problem is "translated" into mathematics, results to the differential equation

where  denotes time,
denotes time,  is the initial population, and
is the initial population, and  ,
,  are constants associated with the growth rate and the carrying capacity of the population. A more general form of (1.1), which will be used in this paper, is
are constants associated with the growth rate and the carrying capacity of the population. A more general form of (1.1), which will be used in this paper, is

where  and
and  ,
,  ,
,  are real constants with
are real constants with  (in order to exclude trivial cases).
(in order to exclude trivial cases).
Equation (1.2) can be regarded as a Bernoulli differential equation or it can be solved by applying the simplest method of separation of variables. In any case, the solution of the initial value problem (1.2) is given by

Although, (1.2) can be considered as a simple differential equation, in the sense that it is completely solvable by use of elementary techniques of the theory of differential equations, it has tremendous and numerous applications in various fields. The first application of (1.2) was already mentioned, and it is connected with population problems, and more generally, problems in ecology. Other applications of (1.2) appear in problems of chemistry, medicine (especially in modelling the growth of tumors), pharmacology (especially in the production of antibiotic medicines) [1], epidemiology [2, 3], atmospheric pollution, flow in a river [4], and so forth.
Nowadays, the logistic differential equation can be found in many biology textbooks and can be considered as a cornerstone of ecology. However, it has also received much criticism by several ecologists. One may find the basis of these criticisms and several paradoxes in [5].
However, as it often happens in applications, when modelling a realistic problem, one may decide to describe the problem in terms of differential equations or in terms of difference equations. Thus, the initial value problem (1.2) which describes the population problem studied by Verhulst, could be formulated instead as an initial value problem of a difference equation. Also, there is a great literature on topics regarding discrete analogues of the differential calculus. In this context, the general difference equation

has been known as the discrete logistic equation and it serves as an analogue to the initial value problem (1.2) (see, e.g., [6]).
There are several ways to "end up" with (1.4) starting from (1.1) or (1.2) as:
-
(a)
by iterating the function
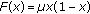 ,
,  ,
, 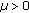 which gives rise to the difference equation [7, page 43]
which gives rise to the difference equation [7, page 43]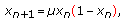 (1.5)
(1.5) -
(b)
by discretizing (1.1) using a forward difference scheme for the derivative, which gives rise to the difference equation
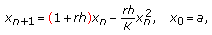 (1.6)
(1.6)where
 ,
,  being the step size of the scheme [8], or
being the step size of the scheme [8], or -
(c)
by "translating" the population problem studied by Verhulst in terms of differences: if
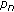 is the population under study at time
is the population under study at time  , its growth is indicated by
, its growth is indicated by 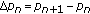 . Thus, according to the assumptions
. Thus, according to the assumptions  and
and 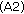 , the following initial value problem appears:
, the following initial value problem appears: (1.7)
(1.7)Notice of course that all three equations (1.5)–(1.7) are special cases of (1.4).
The similarities between (1.2) and (1.4) are obvious even at a first glance. However, these similarities are only superficial, since there are many qualitative differences between their solutions. Perhaps the most important difference between (1.2) and (1.4) is that in contrast to (1.2), (the solution of which is given explicitly in (1.3)) (1.4) (or even its simplest form (1.5)) cannot be solved explicitly so as to obtain its solution in closed form (except for certain values of the parameters) (see, e.g., [6, page 120] and [7, page 14]).
Also, (1.4) is one of the simplest examples of discrete autonomous equations leading to chaos, whereas the solution (1.3) of (1.2) guarantees the regularity of (1.2). Finally, it worths mentioning that the numerical scheme (1.6) or other nonlinear difference equations approximations of (1.2) given for example in [6, page 120] or in [8, pages 297–303] gives rise to approximate solutions of (1.2), which are qualitatively different from the true solution (1.3). These solutions are many times referred to as spurious solutions. These spurious solutions "disappear" when better approximations are used, for example, by applying nonstandard difference schemes (see, e.g., [9–11]).
Recently, in [12, 13] a nonstandard way was proposed for solving "numerically" an ordinary differential equation accompanied with initial or boundary conditions in the real or complex plane. This method was successfully applied to the Duffing equation, the Lorenz system, and the Blasius equation. The technique used is based on the equivalent transformation of the ordinary differential equation under consideration to an ordinary difference equation through an operator equation utilizing a specific isomorphism in specific Banach spaces. One of the aims of the present paper is to apply this technique to (1.2) so as to obtain the following equation:

where  ,
,  are constants, which in the rest of the paper will be calleddiscrete equivalent logistic equation. It should be mentioned at this point that although the application of the technique in [12] to (1.2) is interesting on each own, its side effect, that is, the derivation of (1.8) is more important, since it is proposed as the discrete equivalent of (1.2). It is also emphasized that (1.8) is the discrete equivalent logistic equation derived by straightforward analytical means unlike the known versions of discrete logistic equation such as (1.4). Thus, the solutions of (1.8) are expected to have similar behavior with those of the differential logistic equation and not the peculiar characteristics appearing in the solutions of (1.4) discussed above. Conclusively it is the main aim of the present paper to convince the reader, that (1.8) deserves to be called discrete equivalent logistic equation. It is also hoped that (1.8) could be a better choice for the modelling of various problems, where different versions of known discrete logistic equations are used until nowadays.
are constants, which in the rest of the paper will be calleddiscrete equivalent logistic equation. It should be mentioned at this point that although the application of the technique in [12] to (1.2) is interesting on each own, its side effect, that is, the derivation of (1.8) is more important, since it is proposed as the discrete equivalent of (1.2). It is also emphasized that (1.8) is the discrete equivalent logistic equation derived by straightforward analytical means unlike the known versions of discrete logistic equation such as (1.4). Thus, the solutions of (1.8) are expected to have similar behavior with those of the differential logistic equation and not the peculiar characteristics appearing in the solutions of (1.4) discussed above. Conclusively it is the main aim of the present paper to convince the reader, that (1.8) deserves to be called discrete equivalent logistic equation. It is also hoped that (1.8) could be a better choice for the modelling of various problems, where different versions of known discrete logistic equations are used until nowadays.
Equation (1.8) is a nonlinear Volterra difference equation of convolution type. The Volterra difference equations have been thoroughly studied, and there exists an enormous literature for them. For example, there are several results concerning the boundedness, asymptotic behavior, admissibility, and periodicity of the solution of a Volterra difference equation. Although the list of papers cited in the present work is by no means exhaustive, the review papers [14, 15] on the boundedness, stability, and asymptoticity of Volterra difference equations should be mentioned (see also the references in these two papers). Indicatively, one could also mention the papers [16–32], the general results of which can also be applied to convolution-type Volterra difference equations. Also, in [33–36], linear Volterra difference equations of convolution type are exclusively studied.
In Section 2, (1.8) is fully derived. Moreover, in the same section conditions are given for the existence of a unique solution of (1.2) in the Banach space

where  and of (1.8) in the Banach space
and of (1.8) in the Banach space

It should be mentioned at this point that the issue of the existence of a unique solution in  of the discrete analogue logistic equation (1.4) has been studied in [37] under the framework of a more general difference equation.
of the discrete analogue logistic equation (1.4) has been studied in [37] under the framework of a more general difference equation.
In Section 3, (1.8) is explicitly solved by applying the  -transform method. Finally, in Section 4, several differences between (1.4) and (1.8) are discussed. These differences concern their solutions (see Figure 1), their bifurcation diagrams, and their stability.
-transform method. Finally, in Section 4, several differences between (1.4) and (1.8) are discussed. These differences concern their solutions (see Figure 1), their bifurcation diagrams, and their stability.
2. Derivation of the Discrete Equivalent Logistic Equation
In this section, the method proposed in [12, 13] will be applied to (1.2). As already mentioned in the introduction, the main idea is to transform (1.2) into an equivalent operator equation in an abstract Banach space and from this to deduce the equivalent difference equation (1.8). This method can be applied only when the ordinary differential equation under consideration is studied in the Banach space  defined by (1.9). Moreover, the solution of (1.8), which will eventually give the solution of (1.2), belongs to the Banach space of absolutely summable sequences
defined by (1.9). Moreover, the solution of (1.8), which will eventually give the solution of (1.2), belongs to the Banach space of absolutely summable sequences  defined by (1.10).
defined by (1.10).
2.1. Basic Definitions and Propositions
First of all, define the Hilbert space  by
by

where  . Denote now by
. Denote now by  an abstract separable Hilbert space over the real field, with the orthonormal base
an abstract separable Hilbert space over the real field, with the orthonormal base  ,
,  Denote by
Denote by  and
and  the inner product and the norm in
the inner product and the norm in  , respectively. Define also in
, respectively. Define also in  the shift operator
the shift operator  and its adjoint
and its adjoint 

as well as the diagonal operator 

Proposition 2.1.
The representation

is a one-by-one mapping from  onto
onto  which preserves the norm, where
which preserves the norm, where  ,
,  , is the complete system in
, is the complete system in  of eigenvectors of
of eigenvectors of  and
and  an element of
an element of  [38].
[38].
The unique element  appearing in (2.4) is called theabstract form of
appearing in (2.4) is called theabstract form of  in
in  . In general, if
. In general, if  is a function from
is a function from  to
to  and
and  is the unique element in
is the unique element in  for which
for which

then  is called the abstract form of
is called the abstract form of  in
in  .
.
Consider now the linear manifold of all  which satisfy the condition
which satisfy the condition  . Define the norm
. Define the norm  . Then, this manifold becomes the Banach space
. Then, this manifold becomes the Banach space  defined by (1.9). Denote also by
defined by (1.9). Denote also by  the corresponding by the representation (2.4), abstract Banach space of the elements
the corresponding by the representation (2.4), abstract Banach space of the elements  for which
for which  .
.
The following properties hold [38–40]:
-
(1)
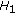 is invariant under the operators
is invariant under the operators  ,
,  ,
,  as well as under every bounded diagonal operator;
as well as under every bounded diagonal operator; -
(2)
the abstract form of
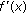 is the element
is the element  , that is,
, that is,  ;
; -
(3)
the abstract form of
 is the element
is the element  , that is,
, that is, 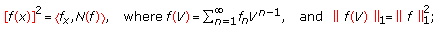 (2.6)
(2.6) -
(4)
the operator
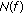 is the Frechét differentiable in
is the Frechét differentiable in  .
.
Proposition 2.2.
The linear function

is an isomorphism from  onto
onto  , that is, it is a 1 − 1 mapping from
, that is, it is a 1 − 1 mapping from  onto
onto  which preserves the norm [37].
which preserves the norm [37].
Remark 2.3.
The basic Propositions 2.1 and 2.2 were originally proved for complex valued sequences and functions ( also in
also in  ), as well as for
), as well as for  ,
,  defined over the complex field. However, in the present paper a restriction to the real plane is made due to the physical applications of the logistic equation.
defined over the complex field. However, in the present paper a restriction to the real plane is made due to the physical applications of the logistic equation.
2.2. Derivation of (1.8)
In order to apply the method of [12, 13] to the logistic differential equation (1.2), it is considered that  ,
,  finite and (1.2) is restricted to
finite and (1.2) is restricted to  by using the simple transformation
by using the simple transformation  ,
,  . Then, (1.2) becomes
. Then, (1.2) becomes

Using Proposition 2.1 and what mentioned in Section 2.1, (2.8) is rewritten as

which holds for all  ,
,  . But
. But  is the complete system in
is the complete system in  of eigenvectors of
of eigenvectors of  , which gives the following equivalent operator equation:
, which gives the following equivalent operator equation:

By taking the inner product of both parts of (2.10) with  and taking into consideration Proposition 2.2 one obtains
and taking into consideration Proposition 2.2 one obtains

where  ,
,  , which is (1.8), the discrete equivalent logistic equation. It is obvious that in (2.11), it is
, which is (1.8), the discrete equivalent logistic equation. It is obvious that in (2.11), it is  and that
and that  , since
, since  and
and  .
.
Of course, for all the above to hold, one has to assure that  and
and  . This is guaranteed by the theorems presented in the next section.
. This is guaranteed by the theorems presented in the next section.
2.3. Existence and Uniqueness Theorems
As mentioned in Section 2.2, conditions must be found so that  and
and  . In order to do so, it is helpful to work with the operator equation (2.10), which is equivalent to both (2.8) and (2.11). Equation (2.10) can be rewritten as
. In order to do so, it is helpful to work with the operator equation (2.10), which is equivalent to both (2.8) and (2.11). Equation (2.10) can be rewritten as

where  is the bounded operator
is the bounded operator  ,
,  or as
or as

due to the definition of  , where
, where  is a constant which can be defined by taking the inner product of both parts of (2.13) with the element
is a constant which can be defined by taking the inner product of both parts of (2.13) with the element  . Indeed, this gives
. Indeed, this gives

since  . Thus (2.13) becomes
. Thus (2.13) becomes

In order to assure the existence of a unique solution of the nonlinear operator equation (2.15) in  , some conditions must be imposed on the parameters appearing in the equation. Moreover, since it is a non linear equation, a fixed-point theorem would be useful. Indeed, the following well-known theorems concerning the inversion of linear operators and the existence of a unique fixed point of an equation will be used.
, some conditions must be imposed on the parameters appearing in the equation. Moreover, since it is a non linear equation, a fixed-point theorem would be useful. Indeed, the following well-known theorems concerning the inversion of linear operators and the existence of a unique fixed point of an equation will be used.
Theorem 2.4.
If  is a linear bounded operator of a Hilbert space
is a linear bounded operator of a Hilbert space  or a Banach space
or a Banach space  , with
, with  , then
, then  is invertible with
is invertible with  and is defined on all
and is defined on all  or
or  (see, e.g., [41, pages 70-71] ).
(see, e.g., [41, pages 70-71] ).
Theorem 2.5.
If  is holomorphic, that is, its Fréchet derivative exists, and
is holomorphic, that is, its Fréchet derivative exists, and  lies strictly inside
lies strictly inside  , then
, then  has a unique fixed point in
has a unique fixed point in  , where
, where  is a bounded, connected, and open subset of a Banach space
is a bounded, connected, and open subset of a Banach space  . (By saying that a subset
. (By saying that a subset  of
of  lies strictly inside
lies strictly inside  , it is meant that there exists an
, it is meant that there exists an  such that
such that  for all
for all  and
and  ) [42].
) [42].
If it is assumed that

then  and due to Theorem 2.4, the operator
and due to Theorem 2.4, the operator  is defined on all
is defined on all  and is bounded by
and is bounded by  . Thus, (2.15) takes the form
. Thus, (2.15) takes the form

from which one finds that

Suppose that  . Then, from (2.18) it is obvious that
. Then, from (2.18) it is obvious that

Define the function  , which attains its maximum
, which attains its maximum  at the point
at the point  . Then, for
. Then, for  ,
,  , it follows that if
, it follows that if

or if

then (2.19) gives  , which means that Theorem 2.5 is applied to (2.17). Thus, the following has just been proved.
, which means that Theorem 2.5 is applied to (2.17). Thus, the following has just been proved.
Theorem 2.6.
If conditions (2.16) and (2.21) hold, then the abstract operator equation (2.10) has a unique solution in  bounded by
bounded by  .
.
Equivalently, this theorem can be "translated" to the following two.
Theorem 2.7.
If conditions (2.16) and (2.21) hold, then the discrete equivalent logistic equation (2.11), has a unique solution in  bounded by
bounded by  .
.
Theorem 2.8.
If conditions (2.16) and (2.21) hold, then the logistic differential equation (1.2) has a unique analytic solution of the form  bounded by
bounded by  , which together with its first derivative converges absolutely for
, which together with its first derivative converges absolutely for  . (The coefficients
. (The coefficients  are defined of course by (2.11)).
are defined of course by (2.11)).
Remark 2.9.
Following the same technique as the one applied for the proof of Theorems 2.6 and 2.7, conditions were given in [37], so that the difference equation (1.4) is to have a unique solution in  or
or  ,
,  . Indeed, it was proved that
. Indeed, it was proved that
-
(a)
if
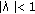 and
and 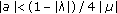 , then (1.4) has a unique solution in
, then (1.4) has a unique solution in  and
and -
(b)
if
 and
and  then (1.4) has a unique solution in
then (1.4) has a unique solution in 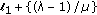 ,
,  .
.
It is obvious that conditions (2.16) and (2.21) are very similar to the conditions derived in [37].
3. Solution of the Discrete Equivalent Logistic Equation
In this section, the discrete equivalent logistic equation (2.11), that is, equation

will be solved by applying the well-known  -transform method (see, e.g., [6, pages 77–82], [7, Chapter 6], and [8, pages 159–172]). Suppose
-transform method (see, e.g., [6, pages 77–82], [7, Chapter 6], and [8, pages 159–172]). Suppose  is the
is the  -transform of the unknown sequence
-transform of the unknown sequence  . It is obvious that
. It is obvious that  is required. However, since
is required. However, since  starts from 1, an "overstepping" should be made, by defining arbitrarily
starts from 1, an "overstepping" should be made, by defining arbitrarily  in such a way so that (3.1) is consistent. Indeed, by setting
in such a way so that (3.1) is consistent. Indeed, by setting  to (3.1), one obtains
to (3.1), one obtains  .
.
Equation (3.1) is of convolution type, and it can be rewritten as

Taking the  -transform of both sides of (3.2), one obtains
-transform of both sides of (3.2), one obtains

which is a Bernoulli differential equation with respect to  . (Remember that the original differential equation (1.2) was also of Bernoulli type!)
. (Remember that the original differential equation (1.2) was also of Bernoulli type!)
The solution of (3.3) is

where  is the arbitrary constant of integration. This constant
is the arbitrary constant of integration. This constant  can be determined by using the following property of this
can be determined by using the following property of this  -transform (since
-transform (since  ):
):

from which it is easily obtained that  . Thus, (3.4) becomes
. Thus, (3.4) becomes

It should be mentioned at this point that since  according to Theorem 2.7, the function
according to Theorem 2.7, the function  defined by (3.6) is analytic for
defined by (3.6) is analytic for  (see [7, Theorem 6.14, page 292] ). By expanding
(see [7, Theorem 6.14, page 292] ). By expanding  , it is found that
, it is found that

which is the solution of (3.1).
Remark 3.1.
The well-known properties of the  -transform
-transform

are of course satisfied.
Remark 3.2.
The solution (3.7) of (3.1) is expected, since the analytic solution (1.3) of (1.2) is known. However, the same technique can be applied to other nonlinear ordinary differential equations of interest for which their analytic solutions are not available. In this sense, a connection between specific ordinary differential and difference equations can be established.
4. Discussion
In this section, a comparison between the solutions of (1.4) and (1.8) will be given. However, since the most commonly used form of the discrete logistic equation is (1.5)

a comparison between the preceding equation and (1.8) for  , that is,
, that is,

will be given.
First of all, something should be mentioned regarding the stability of the equilibrium points of (4.1) and (4.2). At Remark 2.9, it was mentioned that if

equation (4.1) has a unique solution in  , whereas if
, whereas if

equation (4.1) has a unique solution in  .
.
This means that 0 and  are locally asymptotically stable equilibrium points of (4.1) with regions of attraction given by (4.3) and (4.4), respectively. Actually, these results hold for
are locally asymptotically stable equilibrium points of (4.1) with regions of attraction given by (4.3) and (4.4), respectively. Actually, these results hold for  ,
,  , and
, and  complex and not only real as regarded in the present paper (see [37]). However, when restricted to
complex and not only real as regarded in the present paper (see [37]). However, when restricted to  and
and  is not necessary a sequence in
is not necessary a sequence in  the following more general result holds [7, pages 43–45]:
the following more general result holds [7, pages 43–45]:
"The equilibrium point 0 of (4.1) is asymptotically stable for  and unstable for
and unstable for  , and the equilibrium point
, and the equilibrium point  of (4.1) is asymptotically stable for
of (4.1) is asymptotically stable for  and unstable for
and unstable for  ."
."
In a similar way, due to Theorem 2.7, if

equation (4.2) has a unique solution in  , and, thus, 0 is a locally asymptotically stable equilibrium point of the nonautonomous equation (4.2) with region of attraction given by (4.5).
, and, thus, 0 is a locally asymptotically stable equilibrium point of the nonautonomous equation (4.2) with region of attraction given by (4.5).
In Figure 1, the solutions of (4.1) and (4.2) are graphically represented for some representative values of the parameters. More precisely in Figure 1(a), the solutions of (4.1) and (4.2) are given for  and initial conditions
and initial conditions  . For these values, both conditions (4.3) and (4.5) are satisfied and thus these solutions of (4.1) and (4.2) both belong in
. For these values, both conditions (4.3) and (4.5) are satisfied and thus these solutions of (4.1) and (4.2) both belong in  . Moreover, it is obvious from Figure 1(a) that both
. Moreover, it is obvious from Figure 1(a) that both  and
and  exhibit a very similar behavior and of course 0 is an asymptotically stable equilibrium point.
exhibit a very similar behavior and of course 0 is an asymptotically stable equilibrium point.
In Figures 1(b) and 1(c), the solutions of (4.1) and (4.2) are given for  and initial conditions
and initial conditions  and
and  , respectively. For these value of
, respectively. For these value of  , the first condition of both (4.3) and (4.5) is violated. However, it is known that for this value of
, the first condition of both (4.3) and (4.5) is violated. However, it is known that for this value of  , the point
, the point  is an asymptotically stable equilibrium point of (4.1) [7, pages 43–45]. In these cases,
is an asymptotically stable equilibrium point of (4.1) [7, pages 43–45]. In these cases,  and
and  do not exhibit a similar behavior, but both of them tend to a specific point as
do not exhibit a similar behavior, but both of them tend to a specific point as  tends to infinity,
tends to infinity,  to the equilibrium point 0.5 and
to the equilibrium point 0.5 and  to 0. This observation is a quite promising fact that the equilibrium point 0 of (4.2) may remain asymptotically stable even for values of the parameters that do not satisfy (4.5) (since this condition is not necessary and sufficient). However, this needs further study.
to 0. This observation is a quite promising fact that the equilibrium point 0 of (4.2) may remain asymptotically stable even for values of the parameters that do not satisfy (4.5) (since this condition is not necessary and sufficient). However, this needs further study.
Finally, in Figure 1(d), the solutions of (4.1) and (4.2) are given for  and initial conditions
and initial conditions  . For this value of
. For this value of  , the first condition of both (4.3) and (4.5) is again violated. In this case, however,
, the first condition of both (4.3) and (4.5) is again violated. In this case, however,  and
and  exhibit again a very similar behavior, as they both seem to oscillate with continuously growing amplitude to infinity.
exhibit again a very similar behavior, as they both seem to oscillate with continuously growing amplitude to infinity.
Last, but not least, it should be mentioned that as is well known, (4.1) exhibits chaotic behavior and this can be deduced from its period doubling bifurcation diagram [7, page 47]. However, numerical results for (4.2) indicate no chaotic behavior. Actually, its bifurcation diagram is a straight line at 0. For  (which is a region of values for which condition (4.5) is violated),
(which is a region of values for which condition (4.5) is violated),  starts for some initial conditions to "blow up."
starts for some initial conditions to "blow up."
5. Conclusions
In this paper, a discrete equivalent to the well-known logistic differential equation is proposed. This discrete equivalent equation is of the Volterra convolution type and is obtained using a functional-analytic technique. From what mentioned in Sections 3 and 4, it seems that this discrete equivalent logistic equation better resembles the behaviour of the corresponding logistic differential equation in the sense that (a) it can be solved explicitly and (b) it does not seem to present chaotic behaviour. This author believes that although the discrete equivalent logistic equation was derived in a very specific way under the conditions of Theorem 2.6, it would be interesting to further study this equation on its own regardless of conditions with respect to the appearing parameters. In other words, the study of the discrete equivalent logistic equation, not only in the space  but also in several other spaces of sequences, could give rise to interesting results. It would also be interesting to investigate the possibility, (1.8) being useful in the study of biology or physics problems.
but also in several other spaces of sequences, could give rise to interesting results. It would also be interesting to investigate the possibility, (1.8) being useful in the study of biology or physics problems.
References
Dykstra KH, Wang HY: Changes in the protein profile of streptomyces griseus during a cycloheximide fermentation. Annals of the New York Academy of Sciences 1987, 506: 511-522. 10.1111/j.1749-6632.1987.tb23846.x
Brauer F, Castillo-Chávez C: Mathematical Models in Population Biology and Epidemiology, Texts in Applied Mathematics. Volume 40. Springer-Verlag, New York, NY, USA; 2001:xxiv+416.
Hethcote HW: Three basic epidemiological models. In Applied Mathematical Ecology (Trieste, 1986), Biomathematics. Volume 18. Springer, Berlin, Germany; 1989:119-144.
Stoker JJ: Water Waves: The Mathematical Theory with Applications, Pure and Applied Mathematics. Volume 4. Interscience Publishers, New York, NY, USA; 1957:xxviii+567.
Gabriel JP, Saucy F, Bersier L-F: Paradoxes in the logistic equation? Ecological Modelling 2005, 185: 147-151. 10.1016/j.ecolmodel.2004.10.009
Agarwal RP: Difference Equations and Inequalities, Monographs and Textbooks in Pure and Applied Mathematics. Volume 155. Marcel Dekker, New York, NY, USA; 1992:xiv+777. Theory, methods, and application
Elaydi S: An Introduction to Difference Equations, Undergraduate Texts in Mathematics. 3rd edition. Springer, New York, NY, USA; 2005:xxii+539.
Mickens RE: Difference Equations. 2nd edition. Van Nostrand Reinhold, New York, NY, USA; 1990:xii+448. Theory and application
Mickens RE: Nonstandard Finite Difference Models of Differential Equations. World Scientific Publishing, River Edge, NJ, USA; 1994:xii+249.
Mickens RE: Discretizations of nonlinear differential equations using explicit nonstandard methods. Journal of Computational and Applied Mathematics 1999,110(1):181-185. 10.1016/S0377-0427(99)00233-2
Patidar KC: On the use of nonstandard finite difference methods. Journal of Difference Equations and Applications 2005,11(8):735-758. 10.1080/10236190500127471
Petropoulou EN, Siafarikas PD, Tzirtzilakis EE: A "discretization" technique for the solution of ODEs. Journal of Mathematical Analysis and Applications 2007,331(1):279-296. 10.1016/j.jmaa.2006.08.084
Petropoulou EN, Siafarikas PD, Tzirtzilakis EE: A "discretization" technique for the solution of ODEs. II. Numerical Functional Analysis and Optimization 2009,30(5-6):613-631. 10.1080/01630560902987576
Elaydi S: Stability and asymptoticity of Volterra difference equations: a progress report. Journal of Computational and Applied Mathematics 2009,228(2):504-513. 10.1016/j.cam.2008.03.023
Kolmanovskii VB, Castellanos-Velasco E, Torres-Muñoz JA: A survey: stability and boundedness of Volterra difference equations. Nonlinear Analysis. Theory, Methods & Applications 2003,53(7-8):861-928. 10.1016/S0362-546X(03)00021-X
Applelby JAD, Győri I, Reynolds DW: On exact convergence rates for solutions of linear systems of Volterra difference equations. Journal of Difference Equations and Applications 2006,12(12):1257-1275. 10.1080/10236190600986594
Baker CTH, Song Y: Periodic solutions of discrete Volterra equations. Mathematics and Computers in Simulation 2004,64(5):521-542. 10.1016/j.matcom.2003.10.002
Elaydi S, Murakami S: Uniform asymptotic stability in linear Volterra difference equations. Journal of Difference Equations and Applications 1998,3(3-4):203-218. 10.1080/10236199808808097
Gil' MI, Medina R:Nonlinear Volterra difference equations in space
 . Discrete Dynamics in Nature and Society 2004,2004(2):301-306. 10.1155/S1026022604312021
. Discrete Dynamics in Nature and Society 2004,2004(2):301-306. 10.1155/S1026022604312021Győri I, Horváth L: Asymptotic representation of the solutions of linear Volterra difference equations. Advances in Difference Equations 2008, -22.
Győri I, Reynolds DavidW: Sharp conditions for boundedness in linear discrete Volterra equations. Journal of Difference Equations and Applications 2009,15(11-12):1151-1164. 10.1080/10236190902932726
Kolmanovskii VB: Asymptotic properties of the solutions for discrete Volterra equations. International Journal of Systems Science 2003,34(8-9):505-511. 10.1080/00207720310001609048
Kolmanovskii V: Boundedness in average for Volterra nonlinear difference equations. Functional Differential Equations 2005,12(3-4):295-301.
Kolmanovskii V, Shaikhet L: Some conditions for boundedness of solutions of difference Volterra equations. Applied Mathematics Letters 2003,16(6):857-862. 10.1016/S0893-9659(03)90008-5
Medina R, Gil' M: Solution estimates for nonlinear Volterra difference equations. Functional Differential Equations 2004,11(1-2):111-119.
Messina E, Muroya Y, Russo E, Vecchio A: Asymptotic behavior of solutions for nonlinear Volterra discrete equations. Discrete Dynamics in Nature and Society 2008, -18.
Murakami S, Nagabuchi Y: Stability properties and asymptotic almost periodicity for linear Volterra difference equations in a Banach space. Japanese Journal of Mathematics 2005,31(2):193-223.
Song Y: Almost periodic solutions of discrete Volterra equations. Journal of Mathematical Analysis and Applications 2006,314(1):174-194. 10.1016/j.jmaa.2005.03.073
Song Y, Baker CTH: Perturbation theory for discrete Volterra equations. Journal of Difference Equations and Applications 2003,9(10):969-987. 10.1080/1023619031000080844
Song Y, Baker CTH: Linearized stability analysis of discrete Volterra equations. Journal of Mathematical Analysis and Applications 2004,294(1):310-333. 10.1016/j.jmaa.2004.02.019
Song Y, Baker CTH: Admissibility for discrete Volterra equations. Journal of Difference Equations and Applications 2006,12(5):433-457. 10.1080/10236190600563260
Xu Daoyi: Invariant and attracting sets of Volterra difference equations with delays. Computers & Mathematics with Applications 2003,45(6–9):1311-1317. 10.1016/S0898-1221(03)00104-4
Elaydi S: Stability of Volterra difference equations of convolution type. In Dynamical Systems (Tianjin, 1990/1991), Nankai Series in Pure, Applied Mathematics and Theoretical Physics. Volume 4. World Scientific Publishing, River Edge, NJ, USA; 1993:66-72.
Elaydi S, Messina E, Vecchio A: On the asymptotic stability of linear Volterra difference equations of convolution type. Journal of Difference Equations and Applications 2007,13(12):1079-1084. 10.1080/10236190701264529
Elaydi S, Murakami S: Asymptotic stability versus exponential stability in linear Volterra difference equations of convolution type. Journal of Difference Equations and Applications 1996,2(4):401-410. 10.1080/10236199608808074
Tang XH, Jiang Z: Asymptotic behavior of Volterra difference equation. Journal of Difference Equations and Applications 2007,13(1):25-40. 10.1080/10236190601008810
Ifantis EK: On the convergence of power series whose coefficients satisfy a Poincaré-type linear and nonlinear difference equation. Complex Variables. Theory and Application 1987,9(1):63-80. 10.1080/17476938708814250
Ifantis EK: An existence theory for functional-differential equations and functional-differential systems. Journal of Differential Equations 1978,29(1):86-104. 10.1016/0022-0396(78)90042-6
Ifantis EK: Analytic solutions for nonlinear differential equations. Journal of Mathematical Analysis and Applications 1987,124(2):339-380. 10.1016/0022-247X(87)90004-7
Ifantis EK: Global analytic solutions of the radial nonlinear wave equation. Journal of Mathematical Analysis and Applications 1987,124(2):381-410. 10.1016/0022-247X(87)90005-9
Gohberg I, Goldberg S: Basic Operator Theory. Birkhäuser Boston, Boston, Mass, USA; 2001:xiv+285.
Earle CJ, Hamilton RdS: A fixed point theorem for holomorphic mappings. In Global Analysis Proceedings Symposium Pure Mathematics, Vol. XVI, Berkeley, Calif., (1968). American Mathematical Society, Providence, RI, USA; 1970:61-65.
Dedication
This work is dedicated to the memory of the author's Professor, P. D. Siafarikas, who left so early at the age of 57.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Petropoulou, E. A Discrete Equivalent of the Logistic Equation. Adv Differ Equ 2010, 457073 (2010). https://doi.org/10.1155/2010/457073
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/457073
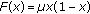 ,
,  ,
, 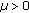 which gives rise to the difference equation [
which gives rise to the difference equation [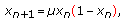
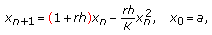
 ,
,  being the step size of the scheme [
being the step size of the scheme [ is the population under study at time
is the population under study at time  , its growth is indicated by
, its growth is indicated by 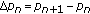 . Thus, according to the assumptions
. Thus, according to the assumptions  and
and 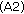 , the following initial value problem appears:
, the following initial value problem appears:

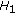 is invariant under the operators
is invariant under the operators  ,
,  ,
,  as well as under every bounded diagonal operator;
as well as under every bounded diagonal operator;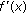 is the element
is the element  , that is,
, that is,  ;
; is the element
is the element  , that is,
, that is, 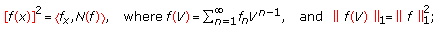
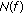 is the Frechét differentiable in
is the Frechét differentiable in  .
.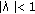 and
and 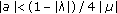 , then (1.4) has a unique solution in
, then (1.4) has a unique solution in  and
and and
and  then (1.4) has a unique solution in
then (1.4) has a unique solution in 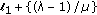 ,
,  .
. . Discrete Dynamics in Nature and Society 2004,2004(2):301-306. 10.1155/S1026022604312021
. Discrete Dynamics in Nature and Society 2004,2004(2):301-306. 10.1155/S1026022604312021