- Research Article
- Open access
- Published:
On Regularly Varying and History-Dependent Convergence Rates of Solutions of a Volterra Equation with Infinite Memory
Advances in Difference Equations volume 2010, Article number: 478291 (2010)
Abstract
We consider the rate of convergence to equilibrium of Volterra integrodifferential equations with infinite memory. We show that if the kernel of Volterra operator is regularly varying at infinity, and the initial history is regularly varying at minus infinity, then the rate of convergence to the equilibrium is regularly varying at infinity, and the exact pointwise rate of convergence can be determined in terms of the rate of decay of the kernel and the rate of growth of the initial history. The result is considered both for a linear Volterra integrodifferential equation as well as for the delay logistic equation from population biology.
1. Introduction
In this paper we consider the asymptotic behaviour of linear and nonlinear Volterra integrodifferential equations with infinite memory, paying particular attention to the connection between the asymptotic behaviour of the initial history as  and the rate of convergence of the solution to a limit. In fact we focus our attention on the cases where the initial history
and the rate of convergence of the solution to a limit. In fact we focus our attention on the cases where the initial history  obeys
obeys  . We do not aim to be comprehensive in our analysis and focus only on scalar equations whose initial histories and kernels are regularly varying functions. However, we note that such history-dependent asymptotic behaviour does not seem to be generic behaviour for equations with a finite memory.
. We do not aim to be comprehensive in our analysis and focus only on scalar equations whose initial histories and kernels are regularly varying functions. However, we note that such history-dependent asymptotic behaviour does not seem to be generic behaviour for equations with a finite memory.
We consider both linear and nonlinear equations. In particular we consider the linear Volterra integrodifferential equation given by

as well as the nonlinear logistic equation with infinite delay given by

In both cases, we presume that  is continuous, positive, and integrable, and that
is continuous, positive, and integrable, and that  is continuous on
is continuous on  . When
. When  is bounded and
is bounded and  , the solution of
, the solution of  of (1.1) obeys
of (1.1) obeys  as
as  ; moreover, Miller [1] has shown when in addition
; moreover, Miller [1] has shown when in addition  , the solution
, the solution  of (1.2) obeys
of (1.2) obeys  as
as  .
.
For definiteness, we concentrate in this introduction on solutions of (1.2). In Appleby et al. [2], an extension of Miller's global asymptotic stability result was given to a class of initial functions  , which can include initial histories
, which can include initial histories  which are unbounded in the sense that
which are unbounded in the sense that  . Furthermore, the rate at which
. Furthermore, the rate at which  converges
converges  as
as  is also of interest.
is also of interest.
It was shown in [2] that for certain classes of kernels  that the rate of convergence of
that the rate of convergence of  to
to  as
as  depends on the asymptotic behaviour of
depends on the asymptotic behaviour of  as
as  . When
. When  is a type of slowly decaying function, called subexponential, it has been shown that when
is a type of slowly decaying function, called subexponential, it has been shown that when

then  tends to zero like
tends to zero like  as
as  . In the case when
. In the case when  tends to a nonzero limit as
tends to a nonzero limit as  ,
,  tends to zero like
tends to zero like  as
as  . Moreover, this rate of decay to zero is slower than
. Moreover, this rate of decay to zero is slower than  . It is therefore of interest to consider how this history-dependent decay rate develops in the case that
. It is therefore of interest to consider how this history-dependent decay rate develops in the case that  is unbounded.
is unbounded.
In our main results, we show that if  decays polynomially (in the sense that
decays polynomially (in the sense that  is in the class of integrable and regularly varying functions) and the history
is in the class of integrable and regularly varying functions) and the history  grows polynomially as
grows polynomially as  (in the sense that
(in the sense that  is a regularly varying function at
is a regularly varying function at  ), and the rate of growth of
), and the rate of growth of  is not too rapid relative to the rate of decay of
is not too rapid relative to the rate of decay of  , then problems (1.1) and (1.2) are well posed and
, then problems (1.1) and (1.2) are well posed and  and
and  as
as  at the rate
at the rate  as
as  .
.
The question of history-dependent asymptotic behaviour is of interest not only in demography and population dynamics, but also in financial mathematics and time series, and this also motivates our study here. It is well known that certain discrete- and continuous-time stochastic processes have autocovariance functions which can be represented as linear difference or delay-differential equations (see, e.g., Küchler and Mensch [3]). In the case of the so-called ARCH ( ) processes which are stationary, the resulting equation for the autocovariance function of the process can be represented as a Volterra summation equation with infinite memory. For details on the stationarity and autocovariance function of such ARCH processes; see, for example, Zaffaroni [4], Giraitis et al. [5], Robinson [6], and Giraitis et al. [7]. In the nonstationary case, the process may be autocorrelated on
) processes which are stationary, the resulting equation for the autocovariance function of the process can be represented as a Volterra summation equation with infinite memory. For details on the stationarity and autocovariance function of such ARCH processes; see, for example, Zaffaroni [4], Giraitis et al. [5], Robinson [6], and Giraitis et al. [7]. In the nonstationary case, the process may be autocorrelated on  is a manner which is inconsistent with the autocovariance function in the stationary case (which must be an even function), while the mean and variance of the process still converge. Therefore, the process can have a limiting autocovariance function which may differ from that of the stationary process. This phenomenon is impossible for processes with bounded memory, and the different convergence rates which depend on the asymptotic behaviour of the initial history in this case is an exact analogue to the history-dependent decay rates recorded here. Therefore, this paper also lays the groundwork for analysis of this phenomenon in finance from the perspective of infinite memory Volterra equations. The interest in such so-called long memory stems in part from the presence of inefficiency in financial markets and the applicability of ARCH-type processes in modelling the evolution of market volatility. Some of the fundamental papers in this direction are Comte and Renault [8], Baillie et al. [9], and Bollerslev and Mikkelsen [10]. An up-to-date survey of work on long memory processes is given by Cont [11].
is a manner which is inconsistent with the autocovariance function in the stationary case (which must be an even function), while the mean and variance of the process still converge. Therefore, the process can have a limiting autocovariance function which may differ from that of the stationary process. This phenomenon is impossible for processes with bounded memory, and the different convergence rates which depend on the asymptotic behaviour of the initial history in this case is an exact analogue to the history-dependent decay rates recorded here. Therefore, this paper also lays the groundwork for analysis of this phenomenon in finance from the perspective of infinite memory Volterra equations. The interest in such so-called long memory stems in part from the presence of inefficiency in financial markets and the applicability of ARCH-type processes in modelling the evolution of market volatility. Some of the fundamental papers in this direction are Comte and Renault [8], Baillie et al. [9], and Bollerslev and Mikkelsen [10]. An up-to-date survey of work on long memory processes is given by Cont [11].
2. Mathematical Preliminaries
We introduce some standard notation. We denote by  the set of real numbers. If
the set of real numbers. If  is an interval in
is an interval in  and
and  a finite dimensional normed space, we denote by
a finite dimensional normed space, we denote by  the family of continuous functions
the family of continuous functions  . The space of Lebesgue integrable functions
. The space of Lebesgue integrable functions  will be denoted by
will be denoted by  . Where
. Where  is clear from the context we omit it from the notation.
is clear from the context we omit it from the notation.
The convolution of  and
and  is denoted by
is denoted by  and defined to be the function given by
and defined to be the function given by

If the domain of  contains an interval of the form
contains an interval of the form  and
and  , then
, then  denotes
denotes  , if it exists.
, if it exists.
2.1. Subexponential and Regularly Varying Functions
We make a definition, based on the hypotheses of Theorem  of [12].
of [12].
Definition 2.1.
Let  be a continuous function. Then we say that
be a continuous function. Then we say that  is subexponential if
is subexponential if



In [13] the terminology positive subexponential function was used instead of just subexponential function. Because subexponential functions play the role here of weight functions, it is natural that they have strictly positive values. The nomenclature subexponential is suggested by the fact that (2.4) implies that, for every  as
as  . This is proved, for example, in [14]. It is also true that
. This is proved, for example, in [14]. It is also true that

In Definition 2.1 above, condition (2.3) can be replaced by

and this latter condition often proves to be useful in proofs.
The properties of subexponential functions have been extensively studied, for example, in [12–15]. Simple examples of subexponential functions are  for
for  ,
,  for
for  and
and  . The class of subexponential functions therefore includes a wide variety of functions exhibiting polynomial and slower-than-exponential decay: nor is the slower-than-exponential decay limited to a class of polynomially decaying functions.
. The class of subexponential functions therefore includes a wide variety of functions exhibiting polynomial and slower-than-exponential decay: nor is the slower-than-exponential decay limited to a class of polynomially decaying functions.
In this paper, however, we restrict our attention to an important subclass of subexponential functions. It is noted in [13] that the class of subexponential functions includes all positive, continuous, integrable functions which are regularly varying at infinity. We recall that a function  is said to be regularly varying at infinity with index
is said to be regularly varying at infinity with index  if
if

and we write  . When
. When  is subexponential. A useful property of a continuous function
is subexponential. A useful property of a continuous function  for
for  is
is

In this paper, we also find it convenient to consider functions in  for
for  . We list some of the important properties used here. A characteristic of regularly varying functions of nonzero index is that they exhibit a type of power-law growth or decay as
. We list some of the important properties used here. A characteristic of regularly varying functions of nonzero index is that they exhibit a type of power-law growth or decay as  . Indeed, if
. Indeed, if  , then
, then

Hence  as
as  if
if  and
and  as
as  if
if  .
.
If  for
for  (and
(and  as
as  ), then
), then  is asymptotic to a continuous function
is asymptotic to a continuous function  , which is also in
, which is also in  , such that
, such that  is increasing on
is increasing on  . Similarly, if
. Similarly, if  for
for  , and
, and  is ultimately positive, then
is ultimately positive, then  is asymptotic to a continuous function
is asymptotic to a continuous function  , which is also in
, which is also in  , such that
, such that  is decreasing on
is decreasing on  .
.
A function  is said to be regularly varying at minus infinity with index
is said to be regularly varying at minus infinity with index  if the function
if the function  defined for
defined for  by
by  is in
is in  . We denote the class of regularly varying functions at minus infinity with index
. We denote the class of regularly varying functions at minus infinity with index  by
by  .
.
For further details on regularly varying functions, consult [16].
3. Existence and Asymptotic Behaviour of Functionals of the Initial History
3.1. Hypotheses on 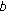 and
and 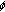
We make the following standing hypotheses concerning the kernel  and initial history
and initial history  of (1.1) and (1.2)
of (1.1) and (1.2)


We introduce a function  which depends on the continuous function
which depends on the continuous function  . Suppose that
. Suppose that



Following [2], we define by  the space of initial functions
the space of initial functions  for which such
for which such  exists and has the properties ((3.3b)) and (3.3c):
exists and has the properties ((3.3b)) and (3.3c):

The importance of  and
and  in this paper is the following. Suppose that we have an infinite memory integrodifferential equation with solution
in this paper is the following. Suppose that we have an infinite memory integrodifferential equation with solution  and initial history
and initial history  , that is,
, that is,  for
for  . If the equation involves a convolution term of the form
. If the equation involves a convolution term of the form

on the right-hand side, the infinite memory equation is equivalent to an initial value integrodifferential equation with unbounded memory, provided that  is such that (3.3a) holds. The existence and uniqueness of a solution of the integrodifferential equation is essentially guaranteed by ((3.3b)), and asymptotic analysis (and in particular stability) is aided by (3.3c). Therefore the class of initial histories
is such that (3.3a) holds. The existence and uniqueness of a solution of the integrodifferential equation is essentially guaranteed by ((3.3b)), and asymptotic analysis (and in particular stability) is aided by (3.3c). Therefore the class of initial histories  helps us to recast questions about the existence, uniqueness, and asymptotic stability of solutions of an infinite memory convolution equation in terms of a perturbed initial value convolution equation, where
helps us to recast questions about the existence, uniqueness, and asymptotic stability of solutions of an infinite memory convolution equation in terms of a perturbed initial value convolution equation, where  , to a certain extent, plays the role of a forcing term or perturbation.
, to a certain extent, plays the role of a forcing term or perturbation.
We now impose some additional conditions on  and
and  which enable us to demonstrate that
which enable us to demonstrate that  and which are also central to the asymptotic analysis of solutions of (1.1) and (1.2). To this end suppose that
and which are also central to the asymptotic analysis of solutions of (1.1) and (1.2). To this end suppose that  obeys
obeys

In addition to (3.2),  also obeys
also obeys

Suppose further that

It is often convenient to work with the function  defined by
defined by  for
for  , rather than with
, rather than with  itself. An important property of
itself. An important property of  is that it is in
is that it is in  .
.
By virtue of the fact that  is regularly varying at infinity with index
is regularly varying at infinity with index  , it follows that there exists a function
, it follows that there exists a function  such that
such that

and  is also forced to satisfy
is also forced to satisfy

Also, because  is regularly varying at infinity with index
is regularly varying at infinity with index  , there exists a function
, there exists a function  which is increasing and which obeys
which is increasing and which obeys  as
as  .
.
3.2. Existence and Asymptotic Behaviour of 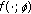
Our results in this section demonstrate that, under the hypotheses (3.6) and (3.7),  has the properties given in (3.3a), (3.3b), and (3.3c). The proofs of the main results are postponed to later in the paper.
has the properties given in (3.3a), (3.3b), and (3.3c). The proofs of the main results are postponed to later in the paper.
Remark 3.1.
Condition (3.8) implies that

It can be seen that (3.11) is necessary for the existence of  for
for  (i.e., for the validity of (3.3a)). This is because the integral in (3.11) is
(i.e., for the validity of (3.3a)). This is because the integral in (3.11) is  .
.
Condition (3.11) is close to being sufficient for the existence of  and indeed is sufficient if
and indeed is sufficient if  and
and  are nonnegative. In fact, because
are nonnegative. In fact, because  is integrable, we have that
is integrable, we have that  as
as  .
.
Proposition 3.2.
Suppose that  obeys (3.1) and (3.6) and that
obeys (3.1) and (3.6) and that  obeys (3.2) and (3.7). If
obeys (3.2) and (3.7). If  and
and  obey (3.8), then
obey (3.8), then  and
and  obey
obey

and  exists for all
exists for all  and therefore obeys (3.3a). Moreover
and therefore obeys (3.3a). Moreover  obeys (3.3c).
obeys (3.3c).
It is notable that condition (3.12) does not require that  be bounded, but merely that it cannot grow too quickly as
be bounded, but merely that it cannot grow too quickly as  , relative to the rate of decay of
, relative to the rate of decay of  as
as  . This is the significance of the parameter restriction (3.8). Scrutiny of the proof, which is in Section 7, reveals that the regular variation of
. This is the significance of the parameter restriction (3.8). Scrutiny of the proof, which is in Section 7, reveals that the regular variation of  and
and  is used sparingly. Indeed, if one assumes (3.12), the properties (3.9) and (3.10) suffice to prove the result.
is used sparingly. Indeed, if one assumes (3.12), the properties (3.9) and (3.10) suffice to prove the result.
Conditions (3.9) and (3.10) will be used to establish the continuity of  , as well as for later asymptotic analysis of
, as well as for later asymptotic analysis of  as
as  .
.
We notice that by virtue of (3.9) that  as
as  . Since
. Since  is also continuous, it follows that it is uniformly continuous. This fact is used at important points in the proof of the following result.
is also continuous, it follows that it is uniformly continuous. This fact is used at important points in the proof of the following result.
Proposition 3.3.
Suppose that  obeys (3.1) and (3.6) and that
obeys (3.1) and (3.6) and that  obeys (3.2) and (3.7). Since
obeys (3.2) and (3.7). Since  and
and  also obey (3.12), then
also obey (3.12), then  exists for all
exists for all  ,
,  is continuous and
is continuous and  as
as  (i.e.,
(i.e.,  ).
).
A careful reading of the proof (again deferred to Section 7) reveals that it is the properties (3.9) and (3.10), together with (3.12), that are employed, and that the full strength of (3.6) and (3.7) is unnecessary.
Having shown that  obeys all the properties in (3.3a), (3.3b), and (3.3c), including the fact that
obeys all the properties in (3.3a), (3.3b), and (3.3c), including the fact that  as
as  , our first main result determines the exact rate of decay to zero of
, our first main result determines the exact rate of decay to zero of  as
as  . In contrast to the other results in this section, the proof of this result employs extensively the regular variation of
. In contrast to the other results in this section, the proof of this result employs extensively the regular variation of  and of
and of  .
.
Theorem 3.4.
Suppose that  is a positive continuous function which obeys (3.6) for some
is a positive continuous function which obeys (3.6) for some  . Let
. Let  be a function which obeys (3.7) for some
be a function which obeys (3.7) for some  , and suppose that
, and suppose that  . Then
. Then  and
and  defined in (3.3a), (3.3b), and (3.3c) obeys
defined in (3.3a), (3.3b), and (3.3c) obeys

The proof of Theorem 3.4 is postponed to Section 5. We note that the integral on the right-hand side of (3.13) exists because  and
and  . We also notice that as
. We also notice that as  and
and  , by (3.13), the function
, by (3.13), the function  .
.
4. Statement and Discussion of Main Results
4.1. Linear Equations with Unbounded Initial History
Once Theorem 3.4 has been proven, we are able to determine the rate of decay of the solution of the following linear infinite memory convolution equation

If we suppose that  and
and  obey merely (3.1) and (3.2), and that
obey merely (3.1) and (3.2), and that  (where
(where  is the space defined by (3.4)), the function
is the space defined by (3.4)), the function  defined in (3.3a), (3.3b), and (3.3c) is well defined and continuous on
defined in (3.3a), (3.3b), and (3.3c) is well defined and continuous on  . Therefore, we see that (4.1) can be written in the equivalent form
. Therefore, we see that (4.1) can be written in the equivalent form

where  for
for  . Since this initial value problem has a unique continuous solution, it follows that there is a unique continuous solution of (4.1). However, as we assume that
. Since this initial value problem has a unique continuous solution, it follows that there is a unique continuous solution of (4.1). However, as we assume that  and
and  obey the hypotheses (3.6), (3.7), (3.1), (3.2), and (3.8) throughout, it follows that
obey the hypotheses (3.6), (3.7), (3.1), (3.2), and (3.8) throughout, it follows that  , and therefore (4.1) has a unique continuous solution
, and therefore (4.1) has a unique continuous solution  .
.
We now investigate conditions under which  as
as  , and the rate of convergence to zero. To study this asymptotic behaviour, it is conventional to introduce the linear differential resolvent
, and the rate of convergence to zero. To study this asymptotic behaviour, it is conventional to introduce the linear differential resolvent  which is defined to be the unique continuous solution of the integrodifferential equation
which is defined to be the unique continuous solution of the integrodifferential equation

The significance of  is that it enables us to represent the unique continuous solution
is that it enables us to represent the unique continuous solution  of (4.1) in terms of
of (4.1) in terms of  (defined in (3.3a)). Using (4.2), the formula for
(defined in (3.3a)). Using (4.2), the formula for  is given by
is given by

In the case when  , it is known that
, it is known that  and
and  as
as  . Therefore, in this case
. Therefore, in this case  as
as  . Some recent results on the asymptotic stability of Volterra equations with unbounded delay include [17, 18].
. Some recent results on the asymptotic stability of Volterra equations with unbounded delay include [17, 18].
Moreover, as  is in
is in  for
for  ,
,  is subexponential, and so it is known by results of, for example, [19], that
is subexponential, and so it is known by results of, for example, [19], that

due to (3.9). Therefore, as we already have good information about the rate of convergence of  as
as  from Theorem 3.4, the representation (4.4) together with (4.5) opens the prospect that the rate of convergence of
from Theorem 3.4, the representation (4.4) together with (4.5) opens the prospect that the rate of convergence of  as
as  can be obtained. Our main result in this direction is as follows.
can be obtained. Our main result in this direction is as follows.
Theorem 4.1.
Suppose that  is a continuous and integrable function which obeys (3.6) for some
is a continuous and integrable function which obeys (3.6) for some  . Let
. Let  be a continuous function which obeys (3.7) for some
be a continuous function which obeys (3.7) for some  and suppose that
and suppose that  . If
. If  , then
, then  , the unique continuous solution of (4.1), obeys
, the unique continuous solution of (4.1), obeys

It is worth re-emphasising that the condition  is not a merely a technical convenience; in the case when
is not a merely a technical convenience; in the case when  for
for  and
and  , problem (4.1) is not well posed, because
, problem (4.1) is not well posed, because  , for example, is not well defined.
, for example, is not well defined.
The proof of Theorem 4.1 is given in Section 6.1, and uses results from the admissibility theory of linear Volterra operators. These results are stated in Section 6, in advance of the proof of Theorem 4.1.
4.2. Delay Logistic Equation with Unbounded Initial History
In this section, we state and discuss a result similar to Theorem 4.1 for a nonlinear integrodifferential equation with infinite memory. We consider the logistic equation with infinite delay

where  is continuous and integrable,
is continuous and integrable,  is continuous, and
is continuous, and  and
and  are real numbers. This equation, and related equations, have been used to study the population dynamics of a single species, where
are real numbers. This equation, and related equations, have been used to study the population dynamics of a single species, where  stands for the population at time
stands for the population at time  .
.
If  is the function given in (3.3a), it is seen that the existence of a solution of (4.7) is equivalent to the existence of a solution of
is the function given in (3.3a), it is seen that the existence of a solution of (4.7) is equivalent to the existence of a solution of

Therefore, it is necessary that the function  be well defined in order for solutions of (4.7) to exist. In the case that
be well defined in order for solutions of (4.7) to exist. In the case that  , then the function
, then the function  given in (3.3a) is well defined and is moreover continuous. Therefore standard results on existence, uniqueness, and continuation of solutions of Volterra integral equations (cf., e.g., Burton [20], Gripenberg et al. [21], Miller [1]) ensure that there is a unique solution of (4.7) (up to a possible explosion time). For the proof of positivity of the solution see, for example, Miller [1]. We state [2, Theorem
given in (3.3a) is well defined and is moreover continuous. Therefore standard results on existence, uniqueness, and continuation of solutions of Volterra integral equations (cf., e.g., Burton [20], Gripenberg et al. [21], Miller [1]) ensure that there is a unique solution of (4.7) (up to a possible explosion time). For the proof of positivity of the solution see, for example, Miller [1]. We state [2, Theorem  ] which concerns on the asymptotic behaviour of solutions of (4.7).
] which concerns on the asymptotic behaviour of solutions of (4.7).
Theorem 4.2.
Let  ,
,  ,
,  . Let
. Let  be defined by (3.4), and suppose that
be defined by (3.4), and suppose that  is also in
is also in  . Then there is a unique continuous positive solution
. Then there is a unique continuous positive solution  of (4.7) which obeys
of (4.7) which obeys

This theorem extends a result of [1] which deals with the case when  is a bounded continuous function. We remark once more that the condition
is a bounded continuous function. We remark once more that the condition  does not require
does not require  to be bounded. Some other recent papers which employ Volterra equations with unbounded delay to model stable population dynamics include [22, 23].
to be bounded. Some other recent papers which employ Volterra equations with unbounded delay to model stable population dynamics include [22, 23].
With Theorem 4.2 in hand, we can determine the convergence rate of the solution  of (4.7) to
of (4.7) to  defined in (4.9).
defined in (4.9).
Theorem 4.3.
Suppose that  is a positive continuous function which obeys (3.6) for some
is a positive continuous function which obeys (3.6) for some  . Let
. Let  and
and  . Let
. Let  obey (3.7) for some
obey (3.7) for some  , and suppose that
, and suppose that  . Then
. Then  , the unique continuous positive solution of (4.7), obeys
, the unique continuous positive solution of (4.7), obeys

where  is defined by (4.9).
is defined by (4.9).
Once again, the proof appeals to results from the admissibility theory of linear Volterra operators. The proof of Theorem 4.3 is deferred to Section 6.2.
It is interesting to compare this result with those obtained for (4.7) under different conditions on  and subexponential
and subexponential  in [2]. Suppose, as in Theorem 4.3 above, that
in [2]. Suppose, as in Theorem 4.3 above, that  ,
,  is continuous and positive, and
is continuous and positive, and  is positive, continuous, and integrable. In the case when
is positive, continuous, and integrable. In the case when  a fortiori obeys (3.6), and there exists
a fortiori obeys (3.6), and there exists  such that
such that

then by [2, Theorem  ] there exists
] there exists  such that
such that

On the other hand, by [2, Theorem  ] we have that
] we have that

implies

In both these cases, there is a history-dependent (i.e., a  -dependent) rate of convergence to the equilibrium; moreover, it appears that the larger the "size" of the history (as measured by the discrepancy of
-dependent) rate of convergence to the equilibrium; moreover, it appears that the larger the "size" of the history (as measured by the discrepancy of  from
from  ), the slower the rate of convergence to
), the slower the rate of convergence to  . In Theorem 4.3 we show that the rate of convergence is slower (
. In Theorem 4.3 we show that the rate of convergence is slower ( as
as  ) than in both (4.12) (
) than in both (4.12) ( as
as  ) and (4.14) (
) and (4.14) ( as
as  ). This is consistent with the picture that a "larger" history leads to a slower rate of convergence, as the history in Theorem 4.3 obeys
). This is consistent with the picture that a "larger" history leads to a slower rate of convergence, as the history in Theorem 4.3 obeys  , in contrast to the "bounded" histories in (4.11) and (4.13). Unbounded histories are studied in [2], but only for equations in which
, in contrast to the "bounded" histories in (4.11) and (4.13). Unbounded histories are studied in [2], but only for equations in which  decays exponentially fast to zero, in the sense that
decays exponentially fast to zero, in the sense that  is subexponential for some
is subexponential for some  , in which case,
, in which case,  can grow as
can grow as  according to
according to

and results similar to (4.14) or (4.12) can be established.
An interesting question, which we do not address here, is to determine the rate of convergence to the equilibrium for solutions of (4.7) in the case when  for
for  . In this case,
. In this case,  is not integrable, but
is not integrable, but  tends to
tends to  as
as  . Therefore, these cases cover histories
. Therefore, these cases cover histories  whose discrepancy from
whose discrepancy from  is intermediate between those
is intermediate between those  covered by conditions (4.13) and (4.11). It might be expected that a similar rate of convergence to zero would be found for solutions of (4.1) in the case when
covered by conditions (4.13) and (4.11). It might be expected that a similar rate of convergence to zero would be found for solutions of (4.1) in the case when  for
for  . Obviously, the key ingredient to proving such results is an analysis of the rate of convergence of
. Obviously, the key ingredient to proving such results is an analysis of the rate of convergence of  as
as  .
.
5. Proof of Theorem 3.4
Theorem 3.4 follows by a number of lemmas. The first part of this section discusses and presents these results; the rest of the section is devoted to their proofs.
5.1. Discussion of Supporting Lemmas
We suppose that  and
and  obey (3.1) and (3.2) throughout. In the first lemma supporting Theorem 3.4, we show that the requirement that
obey (3.1) and (3.2) throughout. In the first lemma supporting Theorem 3.4, we show that the requirement that  and
and  be nonmonotone can essentially be lifted. The key result is the following.
be nonmonotone can essentially be lifted. The key result is the following.
Lemma 5.1.
Suppose that  obeys (3.6) and
obeys (3.6) and  obeys (3.7), then there exist a decreasing continuous function
obeys (3.7), then there exist a decreasing continuous function  such that
such that  as
as  and an increasing function
and an increasing function  such that
such that  as
as  . If there exists
. If there exists  such that
such that

and  is the function defined by (3.3a), then
is the function defined by (3.3a), then

The next result shows that, subject to a technical condition, the conclusion of Theorem 3.4 holds for monotone  and
and  .
.
Lemma 5.2.
Suppose that  is a decreasing and continuous function in
is a decreasing and continuous function in  for
for  , and that
, and that  is an increasing and continuous function in
is an increasing and continuous function in  for
for  . Let
. Let  . If
. If


then

To prove Lemma 5.2, we need the following auxiliary result.
Lemma 5.3.
If  is defined by (5.3) and
is defined by (5.3) and  by (5.4), then
by (5.4), then

Finally, we need to prove the suppositions (5.3) and (5.4).
Lemma 5.4.
If  is a decreasing and continuous function in
is a decreasing and continuous function in  for
for  and
and  for
for  and
and  , then (5.3) and (5.4) hold.
, then (5.3) and (5.4) hold.
The proofs of these lemmas are given in the following subsections. It is readily seen that by taking the results of Lemmas 5.2 and 5.4 together with the result of Lemma 5.1 with  , Theorem 3.4 is true.
, Theorem 3.4 is true.
5.2. Proof of Lemma 5.1
Since  as
as  and
and  as
as  for every
for every  there exists
there exists  such that
such that  for all
for all  and
and  for all
for all  . Therefore
. Therefore


Now

Therefore as  is in
is in  and
and  , we have
, we have  as
as  , and so
, and so

Similarly

Hence by (5.1) we have

Now

so by (5.7) and (5.9)

Similarly by (5.8) and (5.9) we have

Letting  in (5.15) and (5.14) gives (5.2).
in (5.15) and (5.14) gives (5.2).
5.3. Proof of Lemma 5.2
Fix  . Since
. Since  is decreasing and
is decreasing and  is increasing, we have
is increasing, we have

Similarly

Suppose we can show that (5.4) holds, then

Also by (5.3)

Therefore

By (5.20), using the facts that  and
and  , and by employing (5.6), we have (5.5) as required.
, and by employing (5.6), we have (5.5) as required.
5.4. Proof of Lemma 5.3
The required results are


We pause to remark that the integrals on the right-hand side of both (5.21) and (5.22) are finite. To start, notice that


Let  . Let
. Let  be such that
be such that  . Then for
. Then for  we have
we have  and so
and so

Also, as  , for every
, for every  we have
we have  so because
so because  , we have
, we have

This implies

By (5.23), we have

Hence by (5.25) and (5.27) and the fact that  and
and  , we get
, we get

Therefore

Hence

Now

so we have

Letting  yields
yields


By (5.23) and (5.35), we have

Similarly, by (5.24) we have

Combining these inequalities gives (5.21) as required. By (5.34) and (5.21), we get

On the other hand, by (5.23) we have

so by combining these inequalities, we get (5.22) as required.
5.5. Proof of Lemma 5.4
Let  . Since
. Since  is decreasing for
is decreasing for  we have
we have

Since  and
and  are continuous and are in
are continuous and are in  and
and  , respectively, there exists
, respectively, there exists  such that
such that  and
and  for all
for all  . Hence with
. Hence with  and
and  we have
we have

We see that  and
and  is decreasing, while
is decreasing, while  and
and  is increasing. Therefore, we have
is increasing. Therefore, we have

Since  , we may choose
, we may choose  so small that
so small that  . By (5.42), for every
. By (5.42), for every  sufficiently small, there exists
sufficiently small, there exists  such that
such that

Let  be an integer. Then for
be an integer. Then for  we have
we have

For every integer  there exists a unique integer
there exists a unique integer  such that
such that  . Suppose that
. Suppose that  . Then as
. Then as  is decreasing, and
is decreasing, and  is increasing, we have
is increasing, we have

Hence by (5.41) for  , we have
, we have

Define for 

Then for  and
and  we have
we have

Since  , the sequence
, the sequence  is summable. Next, as
is summable. Next, as  and
and  , we have
, we have

Since  for all
for all  , by the summability of
, by the summability of  and (5.49), the Dominated Convergence Theorem gives
and (5.49), the Dominated Convergence Theorem gives

This is equivalent to

which implies (5.3).
To prove that (5.4) holds, note that as  is decreasing and
is decreasing and  is increasing, we have
is increasing, we have

Define

Thus,  for
for  and all
and all  . Also as
. Also as  and
and  , we have
, we have

Now by the summability of  , the last limit and the fact that
, the last limit and the fact that  , by the Dominated Convergence Theorem we have
, by the Dominated Convergence Theorem we have

and therefore (5.4) holds, as required.
6. Proofs of Theorems 4.1 and 4.3
The proofs of Theorems 4.1 and 4.3, which concern the asymptotic behaviour of Volterra equations, are greatly facilitated by applying extant results on the admissibility of certain linear Volterra operators. For the convenience of the reader, two results from [2] are restated.
Let  be a continuous function on
be a continuous function on  . Associated with
. Associated with  is the linear operator
is the linear operator  defined by
defined by

Firstly we restate a theorem, which is a variant of part of a result in Corduneanu [24, page 74].
Theorem 6.1 (see [2, Theorem  ]).
]).
Suppose that for all  ,
,

Further assume that


then  exists for all
exists for all  for which
for which  exists, and
exists, and

The next result is [2, Theorem  ]. It extends Appleby et al. [19, Theorem
]. It extends Appleby et al. [19, Theorem  ] to nonconvolution integral equations (cf. [19, Theorem
] to nonconvolution integral equations (cf. [19, Theorem  ]); it is also the counterpart of Appleby et al. [25, Theorems
]); it is also the counterpart of Appleby et al. [25, Theorems  and
and  ], and Győri and Horváth [26, Theorem
], and Győri and Horváth [26, Theorem  ] which concerns linear nonconvolution difference equations.
] which concerns linear nonconvolution difference equations.
Theorem 6.2 (see [2, Theorem  ]).
]).
Suppose that (6.2) and (6.4) hold, and that (6.3) holds with

Assume that  is in
is in  and that
and that  exists. If
exists. If  is the continuous solution of
is the continuous solution of

then  exists and satisfies the limit formula
exists and satisfies the limit formula

6.1. Proof of Theorem 4.1
The method of [2] is now used to prove Theorems 4.1 and 4.3.
Let  be the positive function defined in (3.9), which is decreasing on
be the positive function defined in (3.9), which is decreasing on  for some
for some  . As remarked the solution
. As remarked the solution  of (4.3) is in
of (4.3) is in  ; it also obeys
; it also obeys

If

holds, then by (4.4), (4.5), and the fact that  as
as  , we have
, we have

which is nothing other than (4.6).
It therefore remains to establish (6.10). Since  for some
for some  there exists
there exists  such that
such that  is increasing on
is increasing on  for some
for some  , positive, differentiable and obeys
, positive, differentiable and obeys  as
as  . Define
. Define  . Then by Theorem 3.4, we have
. Then by Theorem 3.4, we have

Note also that as  as
as  , we have
, we have

Our strategy here is to use Theorem 6.1 to show that  exists and to determine it. To this end write
exists and to determine it. To this end write

where we identify

In the notation of Theorem 6.1,  here plays the role of
here plays the role of  and
and  the role of
the role of  . Evidently
. Evidently  and
and  are continuous. By (6.12), as
are continuous. By (6.12), as  , it follows that
, it follows that  . By (6.13) and (4.5), we have
. By (6.13) and (4.5), we have  . Using this and the fact that
. Using this and the fact that  as
as  uniformly on compact intervals (by (2.4)), we obtain
uniformly on compact intervals (by (2.4)), we obtain

where the convergence is uniform for  , for any
, for any  .
.
Next let  . For
. For  , we have the identity
, we have the identity

Since  obeys (2.4), the second term on the right-hand side has zero limit as
obeys (2.4), the second term on the right-hand side has zero limit as  . As for the first term, by the continuity of
. As for the first term, by the continuity of  and (4.5), the facts that
and (4.5), the facts that  and that
and that  is increasing, we deduce the estimate
is increasing, we deduce the estimate

Since  is subexponential, and therefore obeys (2.3), we have
is subexponential, and therefore obeys (2.3), we have

so it follows that

Therefore by (6.17) and (6.20), we arrive at the estimate

Since  , we have
, we have

Returning to (6.17) we get

Hence by using (6.20), we obtain

Finally, letting  yields
yields

Since all of the hypotheses of Theorem 6.1 are satisfied with  we have, by (6.12) and (6.9),
we have, by (6.12) and (6.9),

which is nothing but (6.10), and so the theorem is proven.
6.2. Proof of Theorem 4.3
First, define  for
for  , where
, where  is given by (4.9). Then by Theorem 4.2,
is given by (4.9). Then by Theorem 4.2,  as
as  . Our strategy, as in [2], is to show that
. Our strategy, as in [2], is to show that  satisfies a linear integral equation (where nonlinearities are subsumed into the kernel and forcing function). Once this is done, we scale the resulting integral equation appropriately and apply Theorem 6.2 to determine the asymptotic behaviour of
satisfies a linear integral equation (where nonlinearities are subsumed into the kernel and forcing function). Once this is done, we scale the resulting integral equation appropriately and apply Theorem 6.2 to determine the asymptotic behaviour of  .
.
Although the same derivation of the integral equation for  is given in [2], we give it afresh here, partly to make the exposition self contained, and partly because it enables us to define and analyse a number of auxiliary functions that will be important in the proof.
is given in [2], we give it afresh here, partly to make the exposition self contained, and partly because it enables us to define and analyse a number of auxiliary functions that will be important in the proof.
Substitution of  into (4.7) with
into (4.7) with  defined by
defined by

leads to the initial-value problem

where  . We note by (3.3a) that the function
. We note by (3.3a) that the function  is well defined, continuous and obeys
is well defined, continuous and obeys  as
as  . Define
. Define

Then  is continuous and
is continuous and  as
as  , and
, and  obeys
obeys

Define the differential resolvent  by
by

Therefore by the variation of constants formula, we have

where

and we have suppressed the  -dependence in
-dependence in  and
and  . Since
. Since  , it follows that
, it follows that  as
as  and
and  with
with

Moreover we have that  exists and is finite. Define
exists and is finite. Define  as in the proof of Theorem 4.1. Dividing (6.32) by
as in the proof of Theorem 4.1. Dividing (6.32) by  , and defining
, and defining  and
and  for
for  we arrive at
we arrive at

where  is given by
is given by

Clearly  ,
,  , and
, and  are continuous. Our strategy now is to apply Theorem 6.2 to determine the integral equation (6.35), showing that
are continuous. Our strategy now is to apply Theorem 6.2 to determine the integral equation (6.35), showing that  tends to a finite limit as
tends to a finite limit as  . From this fact, we will be able to deduce the speed of convergence of
. From this fact, we will be able to deduce the speed of convergence of  to
to  as
as  .
.
First we show that  exists and is finite. Since
exists and is finite. Since  is finite, and
is finite, and  , we have
, we have  . Also with
. Also with  defined by (3.3a),
defined by (3.3a),  for
for  . Since
. Since  for
for  , it obeys
, it obeys

Therefore  , and so we get
, and so we get

by Theorem 3.4. Therefore, by also using the fact that  , we see that
, we see that

by using the argument used to prove (6.26). Hence by (6.34),  obeys
obeys

With  defined by (6.36), we use the facts that
defined by (6.36), we use the facts that  and the fact that
and the fact that  as
as  uniformly on compact intervals to establish that
uniformly on compact intervals to establish that

for all  and any
and any  . Next, as
. Next, as  is uniformly bounded on
is uniformly bounded on  , for any
, for any  , we have
, we have

Therefore by (6.20), we deduce that

Since  is bounded and
is bounded and  , it follows that
, it follows that  obeys
obeys

Hence we also have

and therefore all the conditions of Theorem 6.2 hold, with  . Hence the solution
. Hence the solution  of (6.35) obeys
of (6.35) obeys  . Therefore by (6.40) we have
. Therefore by (6.40) we have

which implies (4.10).
7. Proof of Propositions 3.2 and 3.3
7.1. Proof of Proposition 3.2
By (3.9), (3.12),  is finite, where
is finite, where

By hypothesis

Hence as  is nonincreasing, we have
is nonincreasing, we have

so  , where we define
, where we define

Hence  is uniformly bounded.
is uniformly bounded.
Since  ,
,  is nonincreasing, and
is nonincreasing, and  we have that
we have that  as
as  . Returning to (7.3) with
. Returning to (7.3) with  given by (7.4), we get
given by (7.4), we get

Let  . Then as
. Then as  is nonincreasing, we have
is nonincreasing, we have

The second integral on the right-hand side is finite, and bounded above by  . Since
. Since  is continuous,
is continuous,  is finite. Hence, as
is finite. Hence, as  as
as  , we have
, we have

Since  is arbitrary, and
is arbitrary, and  we have
we have  . Hence
. Hence  , as claimed.
, as claimed.
7.2. Proof of Proposition 3.3
Fix  and let
and let  . We will show for every
. We will show for every  that there exists
that there exists  such that
such that  implies
implies

Assume temporarily that this holds. Then for  , we have
, we have

where we used (7.8) and (7.1) at the last step. This establishes the continuity of  . It remains to prove (7.8). The identity
. It remains to prove (7.8). The identity

applied with  and
and  gives
gives

For every  there exists
there exists  such that
such that

where  is given by (7.1). Suppose also that
is given by (7.1). Suppose also that  so that
so that  . Since
. Since  obeys (3.10), we have
obeys (3.10), we have

Hence for every  there exists
there exists  such that
such that

where  is given by (7.4). Hence as
is given by (7.4). Hence as  we have
we have

Let  . Then as
. Then as  and
and  are nonnegative, using (7.4), (7.12), and (7.15) in (7.11), for
are nonnegative, using (7.4), (7.12), and (7.15) in (7.11), for  we have
we have

Set  . Since
. Since  is uniformly continuous on
is uniformly continuous on  , for every
, for every  there is a
there is a  such that
such that  implies
implies

The  -dependence here is permissible as
-dependence here is permissible as  is fixed. Thus, for
is fixed. Thus, for  ,
,

Let  . By the last inequality and (7.16), for
. By the last inequality and (7.16), for  we get
we get

which is nothing other than (7.8), proving the result.
References
Miller RK: On Volterra's population equation. SIAM Journal on Applied Mathematics 1966, 14: 446-452. 10.1137/0114039
Appleby JAD, Győri I, Reynolds DW: History-dependent decay rates for a logistic equation with infinite delay. submitted
Küchler U, Mensch B: Langevin's stochastic differential equation extended by a time-delayed term. Stochastics and Stochastics Reports 1992,40(1-2):23-42.
Zaffaroni P:Stationarity and memory of
 models. Econometric Theory 2004,20(1):147-160.
models. Econometric Theory 2004,20(1):147-160.Giraitis L, Kokoszka P, Leipus R: Stationary ARCH models: dependence structure and central limit theorem. Econometric Theory 2000,16(1):3-22.
Robinson PM: Testing for strong serial correlation and dynamic conditional heteroskedasticity in multiple regression. Journal of Econometrics 1991,47(1):67-84. 10.1016/0304-4076(91)90078-R
Giraitis L, Robinson PM, Surgailis D: A model for long memory conditional heteroscedasticity. The Annals of Applied Probability 2000,10(3):1002-1024.
Comte F, Renault E: Long memory in continuous-time stochastic volatility models. Mathematical Finance 1998,8(4):291-323. 10.1111/1467-9965.00057
Baillie RT, Bollerslev T, Mikkelsen HO: Fractionally integrated generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 1996,74(1):3-30. 10.1016/S0304-4076(95)01749-6
Bollerslev T, Mikkelsen HO: Modeling and pricing long memory in stock market volatility. Journal of Econometrics 1996,73(1):151-184. 10.1016/0304-4076(95)01736-4
Cont R: Long range dependence in financial markets. In Fractals in Engineering. Edited by: Lutton E, Vehel J. Springer, New York, NY, USA; 2005:159-180.
Chover J, Ney P, Wainger S: Functions of probability measures. Journal d'Analyse Mathématique 1973, 26: 255-302.
Appleby JAD, Reynolds DW: Subexponential solutions of linear integro-differential equations and transient renewal equations. Proceedings of the Royal Society of Edinburgh. Section A 2002,132(3):521-543.
Appleby JAD, Reynolds DW: Subexponential solutions of linear integro-differential equations. In Dynamic Systems and Applications. Volume 4. Dynamic, Atlanta, Ga, USA; 2004:488-494.
Chistyakov VP: A theorem on sums of independent positive random variables and its applications to branching random processes. Theory of Probability and Its Applications 1964, 9: 640-648. 10.1137/1109088
Bingham NH, Goldie CM, Teugels JL: Regular Variation, Encyclopedia of Mathematics and Its Applications. Volume 27. Cambridge University Press, Cambridge, UK; 1989:xx+494.
Murakami S, Nagabuchi Y: Uniform asymptotic stability and robust stability for positive linear Volterra difference equations in Banach lattices. Advances in Difference Equations 2008, 2008:-15.
Philos ChG, Purnaras IK: On linear Volterra difference equations with infinite delay. Advances in Difference Equations 2006, 2006:-28.
Appleby JAD, Győri I, Reynolds DW: On exact rates of decay of solutions of linear systems of Volterra equations with delay. Journal of Mathematical Analysis and Applications 2006,320(1):56-77. 10.1016/j.jmaa.2005.06.103
Burton TA: Stability and Periodic Solutions of Ordinary and Functional-Differential Equations, Mathematics in Science and Engineering. Volume 178. Academic Press, Orlando, Fla, USA; 1985:x+337.
Gripenberg G, Londen S-O, Staffans O: Volterra Integral and Functional Equations, Encyclopedia of Mathematics and Its Applications. Volume 34. Cambridge University Press, Cambridge, UK; 1990:xxii+701.
Choi SK, Koo N: Almost periodic solutions of nonlinear discrete Volterra equations with unbounded delay. Advances in Difference Equations 2008, 2008:-15.
Itokazu T, Hamaya Y: Almost periodic solutions of prey-predator discrete models with delay. Advances in Difference Equations 2009, 2009:-19.
Corduneanu C: Integral Equations and Stability of Feedback Systems, Mathematics in Science and Engineering. Volume 104. Academic Press, New York, NY, USA; 1973:ix+238.
Applelby JAD, Győri I, Reynolds DW: On exact convergence rates for solutions of linear systems of Volterra difference equations. Journal of Difference Equations and Applications 2006,12(12):1257-1275. 10.1080/10236190600986594
Győri I, Horváth L: Asymptotic representation of the solutions of linear Volterra difference equations. Advances in Difference Equations 2008, 2008:-22.
Acknowledgments
The author is grateful to the referees of this paper for their thorough and thoughtful reviews, as well as to the Editor-in-Chief for his suggestions. In addition to the support of Science Foundation Ireland, the author is delighted to thank David Reynolds for many fruitful discussions concerning this work. His criticism and insight of earlier drafts of the manuscript, and particularly his suggestion to streamline the proofs of Theorems 4.1 and 4.3, have greatly improved the final paper. The author is also very grateful to John Daniels for his collaboration and discussions on long-memory time series processes. This has informed the discussion and choice of problems presented in the paper. Finally, the author wishes to thank the editors of this Special Issue of Advances in Difference Equations on "Recent Trends in Differential and Difference Equations" for the opportunity to present his research in this volume. The author gratefully acknowledges Science Foundation Ireland for the support of this research under the Mathematics Initiative 2007 Grant 07/MI/008 "Edgeworth Centre for Financial Mathematics."
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Appleby, J.A.D. On Regularly Varying and History-Dependent Convergence Rates of Solutions of a Volterra Equation with Infinite Memory. Adv Differ Equ 2010, 478291 (2010). https://doi.org/10.1155/2010/478291
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/478291
 and
and 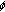
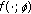
 models. Econometric Theory 2004,20(1):147-160.
models. Econometric Theory 2004,20(1):147-160.