- Research Article
- Open access
- Published:
Asymptotic Behavior of Equilibrium Point for a Family of Rational Difference Equations
Advances in Difference Equations volume 2010, Article number: 505906 (2010)
Abstract
This paper is concerned with the following nonlinear difference equation  where the initial data
where the initial data  ,
,  ,
,  are nonnegative integers, and
are nonnegative integers, and  , B, C, and D are arbitrary positive real numbers. We give sufficient conditions under which the unique equilibrium
, B, C, and D are arbitrary positive real numbers. We give sufficient conditions under which the unique equilibrium  of this equation is globally asymptotically stable, which extends and includes corresponding results obtained in the work of Çinar (2004), Yang et al. (2005), and Berenhaut et al. (2007). In addition, some numerical simulations are also shown to support our analytic results.
of this equation is globally asymptotically stable, which extends and includes corresponding results obtained in the work of Çinar (2004), Yang et al. (2005), and Berenhaut et al. (2007). In addition, some numerical simulations are also shown to support our analytic results.
1. Introduction
Difference equations appear naturally as discrete analogues and in the numerical solutions of differential and delay differential equations, and they have applications in biology, ecology, physics, and so forth [1]. The study of properties of nonlinear difference equations has been an area of intense interest in recent years. There has been a lot of work concerning the globally asymptotic behavior of solutions of rational difference equations (e.g., see [2–5]). In particular, Çinar [6] studied the properties of positive solution to

Yang et al. [7] investigated the qualitative behavior of the recursive sequence

More recently, Berenhaut et al. [8] generalized the result reported in [7] to

For more similar work, one can refer to [9–14] and references therein.
The main theorem in this paper is motivated by the above studies. The essential problem we consider in this paper is the asymptotic behavior of the solutions for

with initial data  are nonnegative integers, and
are nonnegative integers, and  and
and  are arbitrary positive real numbers. In addition, some numerical simulations of the behavior are shown to illustrate our analytic results.
are arbitrary positive real numbers. In addition, some numerical simulations of the behavior are shown to illustrate our analytic results.
This paper proceeds as follows. In Section 2, we introduce some definitions and preliminary results. The main results and their proofs are given in Section 3. Finally, some numerical simulations are shown to support theoretical analysis.
2. Preliminaries and Notations
In this section, we prepare some materials used throughout this paper, namely, notations, the basic definitions, and preliminary results. We refer to the monographs of Kocić and Ladas [2], and Kulenović and Ladas [3].
Let  and
and  be two nonnegative integers such that
be two nonnegative integers such that  . We usually write a vector
. We usually write a vector  with
with  components into
components into , where
, where  denotes a vector with
denotes a vector with  -components of
-components of  .
.
Lemma 2.1.
Let  be some interval of real numbers and
be some interval of real numbers and

be a continuously differentiable function. Then, for every set of initial conditions  ,
,

has a unique solution  .
.
Definition 2.2.
Function  is called mixed monotone in subset
is called mixed monotone in subset  of
of  if
if  is monotone nondecreasing in each component of
is monotone nondecreasing in each component of  and is monotone nonincreasing in every component of
and is monotone nonincreasing in every component of  for
for  .
.
Definition 2.3.
If there exists a point  such that
such that  ,
,  is called an equilibrium point of (2.2).
is called an equilibrium point of (2.2).
Definition 2.4.
Let  be an equilibrium point of (2.2).
be an equilibrium point of (2.2).
-
(1)
The equilibrium
 of (2.2) is (locally) stable if for every
of (2.2) is (locally) stable if for every 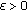 , there exists
, there exists 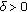 such that for any initial data
such that for any initial data  satisfying
satisfying 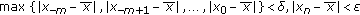 holds for all
holds for all 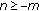 .
. -
(2)
The equilibrium
 of (2.2) is a local attractor if there exists
of (2.2) is a local attractor if there exists 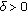 such that
such that 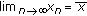 for any data
for any data  satisfying
satisfying  .
. -
(3)
The equilibrium
 of (2.2) is locally asymptotically stable if it is stable and is a local attractor.
of (2.2) is locally asymptotically stable if it is stable and is a local attractor. -
(4)
The equilibrium
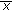 of (2.2) is a global attractor if for all
of (2.2) is a global attractor if for all 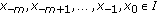 ,
, 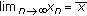 holds.
holds. -
(5)
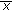 is globally asymptotically stable if it is stable and is a global attractor.
is globally asymptotically stable if it is stable and is a global attractor. -
(6)
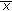 is unstable if it is not locally stable.
is unstable if it is not locally stable.
Lemma 2.5.
Assume that  and
and  . Then,
. Then,

is a sufficient condition for the local stability of the difference equation

3. The Main Results and Their Proofs
In this section, we investigate the globally asymptotic stability of the equilibrium point of (1.4).
It is obvious that  is a unique equilibrium point of (1.4) provided either
is a unique equilibrium point of (1.4) provided either  or
or  .
.
Let  be a multivariate continuous function defined by
be a multivariate continuous function defined by

If  we have
we have

By constructing (1.4) and applying Lemma 2.5, we have the following affirmation.
Theorem 3.1.
If  , and
, and  with
with  , then the unique equilibrium point
, then the unique equilibrium point  of (1.4) is locally stable. If
of (1.4) is locally stable. If  is unstable.
is unstable.
Proof.
Considering the linearized equation of (1.4) with respect to equilibrium point  ,
,

By Lemma 2.5, (1.4) is stable if the following inequality holds

which implies our claim.
When  , note that the solution of (1.4) is
, note that the solution of (1.4) is  , hence
, hence , which implies that
, which implies that  is a dispersed sequence.
is a dispersed sequence.
Theorem 3.2.
Let  defined by (2.2) be a continuous function satisfying the mixed monotone property. If there exists two real numbers
defined by (2.2) be a continuous function satisfying the mixed monotone property. If there exists two real numbers  satisfying
satisfying

such that

then there exists  satisfying
satisfying

Moreover, if  , then (2.2) has a unique equilibrium point
, then (2.2) has a unique equilibrium point  , and every solution of (2.2) converges to
, and every solution of (2.2) converges to  .
.
Proof.
Let  and
and  be a couple of initial iteration data, then we construct two sequences
be a couple of initial iteration data, then we construct two sequences  and
and  in the form
in the form

Note that mixed monotone property of  and initial assumption, the sequences
and initial assumption, the sequences  and
and  thus possess
thus possess

It guarantees one can choose a new sequence  satisfying
satisfying  for
for  .
.
Denote

then

By the continuity of  , we have
, we have

Moreover, if  , then
, then  , and then the proof is complete.
, and then the proof is complete.
Theorem 3.3.
If  ,
, , and
, and  , then the unique equilibrium point
, then the unique equilibrium point of (1.4) is global attractor for any initial conditions
of (1.4) is global attractor for any initial conditions  .
.
Proof.
For any nonnegative initial data  , it is obvious that the function
, it is obvious that the function  defined by (3.1) is nondecreasing in
defined by (3.1) is nondecreasing in  and nonincreasing in
and nonincreasing in  .
.
Let

by view of the assumption  we have
we have

From (1.4) and Theorem 3.2, there exists  satisfying
satisfying

Taking the difference

we deduce that

which implies

where 
By view of  and initial conditions
and initial conditions  , therefore we have
, therefore we have

thus, we have

By Theorem 3.2, then every solution of (1.4) converges to the unique equilibrium point  .
.
Theorem 3.4.
If  , and
, and  , then the unique equilibrium point
, then the unique equilibrium point of (1.4) is globally asymptotically stable for any initial conditions
of (1.4) is globally asymptotically stable for any initial conditions  .
.
Proof.
The result holds from Theorems 3.1 and 3.3.
Theorem 3.5.
If  , and
, and  , then the unique equilibrium point
, then the unique equilibrium point of (1.4) is global attractor for any initial conditions
of (1.4) is global attractor for any initial conditions 
Proof.
The proof of this Theorem is similar to that of Theorem 3.3. We omit the details.
Theorem 3.6.
If  , and
, and  , then the unique equilibrium point
, then the unique equilibrium point of (1.4) is globally asymptotically stable for any initial conditions
of (1.4) is globally asymptotically stable for any initial conditions  .
.
Proof.
The result holds from Theorems 3.1 and 3.5.
4. Numerical Simulation
In this section, we give some numerical simulations supporting our theoretical analysis via the software package Matlab 7.1. As examples, we consider



Let  , it is obvious that (4.1) and (4.2) satisfy the conditions of Theorem 3.6 when the initial datas
, it is obvious that (4.1) and (4.2) satisfy the conditions of Theorem 3.6 when the initial datas  . Equation (4.3) satisfies the conditions of Theorem 3.1 for the initial data
. Equation (4.3) satisfies the conditions of Theorem 3.1 for the initial data  .
.
By employing the software package Matlab 7.1, we can solve the numerical solutions of (4.1), (4.2), and (4.3) which are shown, respectively, in Figures 1, 2, and 3. More precisely, Figure 1 shows the asymptotic behavior of the solution to (4.1) with initial data  and
and  , Figure 2 shows the asymptotic behavior of the solution to (4.2) with initial data
, Figure 2 shows the asymptotic behavior of the solution to (4.2) with initial data  and
and  , and Figure 3 shows the asymptotic behavior of the solution to (4.3) with initial data
, and Figure 3 shows the asymptotic behavior of the solution to (4.3) with initial data  and
and 



5. Conclusions
This paper presents the use of a variational iteration method for systems of nonlinear difference equations. This technique is a powerful tool for solving various difference equations and can also be applied to other nonlinear differential equations in mathematical physics. The numerical simulations show that this method is an effective and convenient one. The variational iteration method provides an efficient method to handle the nonlinear structure. Computations are performed using the software package Matlab 7.1.
We have dealt with the problem of global asymptotic stability analysis for a class of nonlinear difference equation. The general sufficient conditions have been obtained to ensure the existence, uniqueness, and global asymptotic stability of the equilibrium point for the nonlinear difference equation. These criteria generalize and improve some known results. In particular, some examples are given to show the effectiveness of the obtained results. In addition, the sufficient conditions that we obtained are very simple, which provide flexibility for the application and analysis of nonlinear difference equation.
References
Li W-T, Sun H-R: Global attractivity in a rational recursive sequence. Dynamic Systems and Applications 2002,11(3):339-345.
Kocić VL, Ladas G: Global Behavior of Nonlinear Difference Equations of Higher Order with Applications, Mathematics and Its Applications. Volume 256. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1993:xii+228.
Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations with Open Problems and Conjectures. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xii+218.
El-Owaidy HM, Ahmed AM, Mousa MS:On the recursive sequences
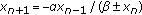 . Applied Mathematics and Computation 2003,145(2-3):747-753. 10.1016/S0096-3003(03)00271-6
. Applied Mathematics and Computation 2003,145(2-3):747-753. 10.1016/S0096-3003(03)00271-6Xianyi X-Y, Zhu D-M: Global asymptotic stability in a rational equation. Journal of Difference Equations and Applications 2003,9(9):833-839. 10.1080/1023619031000071303
Çinar C:On the positive solutions of the difference equation
 . Applied Mathematics and Computation 2004,150(1):21-24. 10.1016/S0096-3003(03)00194-2
. Applied Mathematics and Computation 2004,150(1):21-24. 10.1016/S0096-3003(03)00194-2Yang X, Su W, Chen B, Megson GM, Evans DJ:On the recursive sequence
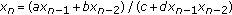 . Applied Mathematics and Computation 2005,162(3):1485-1497. 10.1016/j.amc.2004.03.023
. Applied Mathematics and Computation 2005,162(3):1485-1497. 10.1016/j.amc.2004.03.023Berenhaut KS, Foley JD, Stević S:The global attractivity of the rational difference equation
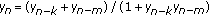 . Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022
. Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022Berenhaut KS, Stević S:The difference equation
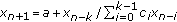 has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088
has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088Memarbashi R: Sufficient conditions for the exponential stability of nonautonomous difference equations. Applied Mathematics Letters 2008,21(3):232-235. 10.1016/j.aml.2007.03.014
Aloqeili M: Global stability of a rational symmetric difference equation. Applied Mathematics and Computation 2009,215(3):950-953. 10.1016/j.amc.2009.06.026
Aprahamian M, Souroujon D, Tersian S: Decreasing and fast solutions for a second-order difference equation related to Fisher-Kolmogorov's equation. Journal of Mathematical Analysis and Applications 2010,363(1):97-110. 10.1016/j.jmaa.2009.08.009
Wang C-y, Gong F, Wang S, Li L-r, Shi Q-h: Asymptotic behavior of equilibrium point for a class of nonlinear difference equation. Advances in Difference Equations 2009, 2009:-8.
Wang C-y, Wang S, Wang Z-w, Gong F, Wang R-f: Asymptotic stability for a class of nonlinear difference equations. Discrete Dynamics in Nature and Society 2010, 2010:-10.
Acknowledgments
The authors are grateful to the referee for giving us lots of precious comments. This work is supported by Natural Science Foundation Project of CQ CSTC (Grant no. 2008BB 7415) of China, and National Science Foundation (Grant no. 40801214) of China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Cy., Shi, Qh. & Wang, S. Asymptotic Behavior of Equilibrium Point for a Family of Rational Difference Equations. Adv Differ Equ 2010, 505906 (2010). https://doi.org/10.1155/2010/505906
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/505906
 of (2.2) is (locally) stable if for every
of (2.2) is (locally) stable if for every 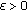 , there exists
, there exists 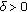 such that for any initial data
such that for any initial data  satisfying
satisfying 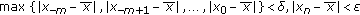 holds for all
holds for all 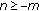 .
. of (2.2) is a local attractor if there exists
of (2.2) is a local attractor if there exists 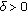 such that
such that 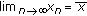 for any data
for any data  satisfying
satisfying  .
. of (2.2) is locally asymptotically stable if it is stable and is a local attractor.
of (2.2) is locally asymptotically stable if it is stable and is a local attractor.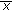 of (2.2) is a global attractor if for all
of (2.2) is a global attractor if for all 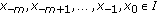 ,
, 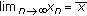 holds.
holds.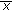 is globally asymptotically stable if it is stable and is a global attractor.
is globally asymptotically stable if it is stable and is a global attractor.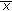 is unstable if it is not locally stable.
is unstable if it is not locally stable.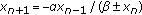 . Applied Mathematics and Computation 2003,145(2-3):747-753. 10.1016/S0096-3003(03)00271-6
. Applied Mathematics and Computation 2003,145(2-3):747-753. 10.1016/S0096-3003(03)00271-6 . Applied Mathematics and Computation 2004,150(1):21-24. 10.1016/S0096-3003(03)00194-2
. Applied Mathematics and Computation 2004,150(1):21-24. 10.1016/S0096-3003(03)00194-2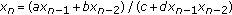 . Applied Mathematics and Computation 2005,162(3):1485-1497. 10.1016/j.amc.2004.03.023
. Applied Mathematics and Computation 2005,162(3):1485-1497. 10.1016/j.amc.2004.03.023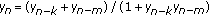 . Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022
. Applied Mathematics Letters 2007,20(1):54-58. 10.1016/j.aml.2006.02.022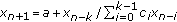 has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088
has solutions converging to zero. Journal of Mathematical Analysis and Applications 2007,326(2):1466-1471. 10.1016/j.jmaa.2006.02.088