- Research Article
- Open access
- Published:
Attractor for a Viscous Coupled Camassa-Holm Equation
Advances in Difference Equations volume 2010, Article number: 512812 (2010)
Abstract
The global existence of solution to a viscous coupled Camassa-Holm equation with the periodic boundary condition is investigated. We obtain the compact and bounded absorbing set and the existence of the global attractor for the viscous coupled Camassa-Holm equation in  by uniform prior estimate.
by uniform prior estimate.
1. Introduction
The Camassa-Holm equation

has been paid considerable attention due to its rich phenomenology all the time. Its abstract derivation was first discovered by Fuchssteiner and Fokas [1], while in the physical derivation of Camassa and Holm (see [2, 3]), the equation models unidirectional propagation of shallow water waves, and  represents the fluid velocity in the
represents the fluid velocity in the direction, equivalently the height of the fluid's free surface above a flat bottom. They also found that the solitary waves interact like solitons. Unlike the Korteweg-de Vries equation (which is an approximation to the equations of motion), this model is obtained by approximating directly in the Hamiltonian for Euler's equations in the shallow water regime (see [3, 4]). Equation (1.1) retains higher-order terms in a small amplitude expansion of incompressible Euler's equations for unidirectional motion of waves at the free surface under the influence of gravity. Dropping these terms leads to the BBM equation, or at the same order, the KdV equation. The Camassa-Holm has quite a few interesting features: it admits solitary waves called "peakons" with the form of
direction, equivalently the height of the fluid's free surface above a flat bottom. They also found that the solitary waves interact like solitons. Unlike the Korteweg-de Vries equation (which is an approximation to the equations of motion), this model is obtained by approximating directly in the Hamiltonian for Euler's equations in the shallow water regime (see [3, 4]). Equation (1.1) retains higher-order terms in a small amplitude expansion of incompressible Euler's equations for unidirectional motion of waves at the free surface under the influence of gravity. Dropping these terms leads to the BBM equation, or at the same order, the KdV equation. The Camassa-Holm has quite a few interesting features: it admits solitary waves called "peakons" with the form of  . The peakons of (1.1) are orbitally stable [5]—that is, their shape is stable under small perturbations and therefore these waves are recognized physically. For waves that approximate the peakons in a special way, a stability result was proved by a variation method [6]. This is in sharp contrast to the Korteweg-de Vries equation, where solitary waves are generally smooth. The peaked traveling waves of the Camassa-Holm equation replicate a future that is characteristic for waves of great height–waves of the largest amplitude that are exact solutions of the governing equations for water waves (see [7, 8]). A breaking wave is a solution which remains bounded but whose slope becomes unbounded in finite time, and, in contrast to the KdV equation, the Camassa-Holm equation models breaking waves [9], as well as a breaking rod (see [4, 10]), since the equation models the propagation of axisymmetric waves in hyperelastic rods. After breaking, the solution can be continued either as a global conservative weak solution or as a global dissipative solution (see [11–13]). Peakons interact "elastically" in the manner typical of all solitons, and their wave dynamics are now wellunderstood (see [3, 14, 15]). Some authors have even argued recently that the Camassa-Holm equation might be relevant to the modeling of tsunamis (see [16, 17]). Moreover, the equation has a bi-Hamiltonian structure [2]. As the Camassa-Holm is completely integrable, it has many conserved qualities. Especially for smooth solutions, the qualities
. The peakons of (1.1) are orbitally stable [5]—that is, their shape is stable under small perturbations and therefore these waves are recognized physically. For waves that approximate the peakons in a special way, a stability result was proved by a variation method [6]. This is in sharp contrast to the Korteweg-de Vries equation, where solitary waves are generally smooth. The peaked traveling waves of the Camassa-Holm equation replicate a future that is characteristic for waves of great height–waves of the largest amplitude that are exact solutions of the governing equations for water waves (see [7, 8]). A breaking wave is a solution which remains bounded but whose slope becomes unbounded in finite time, and, in contrast to the KdV equation, the Camassa-Holm equation models breaking waves [9], as well as a breaking rod (see [4, 10]), since the equation models the propagation of axisymmetric waves in hyperelastic rods. After breaking, the solution can be continued either as a global conservative weak solution or as a global dissipative solution (see [11–13]). Peakons interact "elastically" in the manner typical of all solitons, and their wave dynamics are now wellunderstood (see [3, 14, 15]). Some authors have even argued recently that the Camassa-Holm equation might be relevant to the modeling of tsunamis (see [16, 17]). Moreover, the equation has a bi-Hamiltonian structure [2]. As the Camassa-Holm is completely integrable, it has many conserved qualities. Especially for smooth solutions, the qualities

are all time independent [18].
Up to now, great efforts have been already devoted to the Camassa-Holm equation. A. Constantin (see [19–21]) considered the Cauchy problem, inverse spectral problem, and inverse scatting transform for Camassa-Holm equation, proving that the corresponding solution to (1.1) does not exist globally for smooth initial data. Rui et al. (see [22, 23]) employed both bifurcation method and numerical simulation to investigate bounded traveling waves of (1.1) in a general compressible hyperelastic rod. Lenells [24] used the inverse scattering transform to show that a solution of the Camassa-Holm equation is identically zero whenever it vanishes on two horizontal half-lines in the  space. In particular, a solution that has compact support at two different times vanishes everywhere, proving that the Camassa-Holm equation has infinite propagation speed. Cohen et al. [25] presented two new multisymplectic formulations for the Camassa-Holm equation, and the associated local conservation laws were shown to correspond to certain well-known Hamiltonian functionals. The multisymplectic discretisation of each formulation was exemplified by means of the Euler box scheme. Yiping Meng and Lixin Tian [26] investigated the boundary control of the viscous generalized Camassa-Holm equation on
space. In particular, a solution that has compact support at two different times vanishes everywhere, proving that the Camassa-Holm equation has infinite propagation speed. Cohen et al. [25] presented two new multisymplectic formulations for the Camassa-Holm equation, and the associated local conservation laws were shown to correspond to certain well-known Hamiltonian functionals. The multisymplectic discretisation of each formulation was exemplified by means of the Euler box scheme. Yiping Meng and Lixin Tian [26] investigated the boundary control of the viscous generalized Camassa-Holm equation on  . Long et al. [27] obtained the loop soliton solution and periodic loop soliton solution [28], solitary wave solution and solitary cusp wave solution and smooth periodic wave solution and nonsmooth periodic wave solution of (1.1) and also discussed their dynamic characters and relations by the integral bifurcation method. Moreover, Ding and Tian (see [29, 30]) considered the existence of the global solution to dissipative Camassa-Holm equation and the global attractor of semigroup of solutions of dissipative Camassa-Holm equation in
. Long et al. [27] obtained the loop soliton solution and periodic loop soliton solution [28], solitary wave solution and solitary cusp wave solution and smooth periodic wave solution and nonsmooth periodic wave solution of (1.1) and also discussed their dynamic characters and relations by the integral bifurcation method. Moreover, Ding and Tian (see [29, 30]) considered the existence of the global solution to dissipative Camassa-Holm equation and the global attractor of semigroup of solutions of dissipative Camassa-Holm equation in  . Olson [31] showed that the Cauchy problem for a higher-order modification of (1.1) is locally well posed for initial data in
. Olson [31] showed that the Cauchy problem for a higher-order modification of (1.1) is locally well posed for initial data in  for
for  , where
, where  and the value of
and the value of  depends on the order of equation, proved the existence and uniqueness of solutions of (1.1) by a contraction mapping argument. Moreover, Zhou and Tian [32] investigated the initial boundary value problem of a generalized Camassa-Holm equation with dissipation and established local well-posedness of this closed-loop system by using Kato's theorem for abstract quasilinear evolution equation of hyperbolic type. Then they obtained a conservation law that enables us to present a blowup result by using multiplier technique. Lixin Tian et. al. [33] discussed optimal control of the viscous Camassa-Holm equation; they deduce that the norm of solution is related to the control item and initial value in the special Hilbert space according to variational method, optimal control theories and distributed parameter system control theories, The optimal control of the viscous Camassa-Holm equation under boundary condition was given, and the existence of optimal solution of the viscous Camassa-Holm equation was proved. Well-posedness problem and scattering problem for DGH equation were also discussed in [34].
depends on the order of equation, proved the existence and uniqueness of solutions of (1.1) by a contraction mapping argument. Moreover, Zhou and Tian [32] investigated the initial boundary value problem of a generalized Camassa-Holm equation with dissipation and established local well-posedness of this closed-loop system by using Kato's theorem for abstract quasilinear evolution equation of hyperbolic type. Then they obtained a conservation law that enables us to present a blowup result by using multiplier technique. Lixin Tian et. al. [33] discussed optimal control of the viscous Camassa-Holm equation; they deduce that the norm of solution is related to the control item and initial value in the special Hilbert space according to variational method, optimal control theories and distributed parameter system control theories, The optimal control of the viscous Camassa-Holm equation under boundary condition was given, and the existence of optimal solution of the viscous Camassa-Holm equation was proved. Well-posedness problem and scattering problem for DGH equation were also discussed in [34].
On the basis of deformation of bi-Hamiltonian structure of the hydrodynamic type, Chen et al.[35] obtained the following two-component generalization of (1.1):

Equation (1.3) is one of many multicomponent generalizations which are integrable (see [35–37]). It has a Lax pair, and it is bi-Hamiltonian. Constantin and Ivanov [36] showed how (1.3) arises in shallow water theory, and it was derived from the Green-Naghdi equations by using expansions in terms of physical parameters. Recently, the infinite propagation speed property for (1.3) was proved in [38]. Escher et al. [39] probed into well-posedness and blowup phenomena of the two-component Camassa-Holm equation in details. Chen et al. [35] obtained solutions of (1.3) by a reciprocal transformation between (1.3) and the first negative flow of the AKNS hierarchy and stated some examples of peakon and multikink solutions of (1.3). Guan and Yin [40] presented a new global existence result and several new blowup results of strong solutions to (1.3) as  , improving considerably earlier results. Jibin Li and Yishen Li [41] obtained the existence of solitary wave solutions, kink and antikink wave solutions, uncountable infinite many breaking wave solutions, and smooth and nonsmooth periodic wave solutions with the method of dynamical systems to the two-component generalization of the Camassa-Holm equation. Yujuan Wang et. al.[42] showed that the two-component Camassa-Holm equation possesses a global continuous semigroup of weak conservative solutions for initial data. In [43] a link between central extensions of superconformal algebra and a supersymmetric two-component generalization of the Camassa-Holm equation was concerned. Deformations of superconformal algebra give rise to two compatible bracket structures. For
, improving considerably earlier results. Jibin Li and Yishen Li [41] obtained the existence of solitary wave solutions, kink and antikink wave solutions, uncountable infinite many breaking wave solutions, and smooth and nonsmooth periodic wave solutions with the method of dynamical systems to the two-component generalization of the Camassa-Holm equation. Yujuan Wang et. al.[42] showed that the two-component Camassa-Holm equation possesses a global continuous semigroup of weak conservative solutions for initial data. In [43] a link between central extensions of superconformal algebra and a supersymmetric two-component generalization of the Camassa-Holm equation was concerned. Deformations of superconformal algebra give rise to two compatible bracket structures. For  the system (1.3) particularizes to the Camassa-Holm equation which is a re-expression of geodesic flow on the diffeomorphism group of the circle (see [44, 45]).
the system (1.3) particularizes to the Camassa-Holm equation which is a re-expression of geodesic flow on the diffeomorphism group of the circle (see [44, 45]).
We know that it is of great use to construct an interacting system of equations [37]:

as  and
and  , it, respectively, leads to the Degasperis-Procesi equation and Camassa-Holm equation. Three independent conserved quantities have been obtained as follows:
, it, respectively, leads to the Degasperis-Procesi equation and Camassa-Holm equation. Three independent conserved quantities have been obtained as follows:

here  is an arbitrary constant.
is an arbitrary constant.
Ying Fu and Changzheng Qu [46] considered the following coupled Camassa-Holm equation:

which has peakon solitons in the form of a superposition of multipeakons. It has the following conserved qualities:

They investigated local well-posedness and blowup solutions of (1.6) by means of Kato's semigroup approach to nonlinear hyperbolic evolution equation and obtained a criterion and condition on the initial data guaranteeing the development of singularities in finite time for strong solutions of (1.6) by energy estimates; moreover, an existence result for a class of local weak solutions was also given. They also showed that the solution of (1.6) is

for some positive constants  .
.
In the field of infinite-dimensional dynamical systems, one of the most important issues is to obtain the existence of global attractors for the semigroups of solutions associated with some concrete partial differential equations. For instance, Yongsheng Li and Xingyu Yan [47] studied the existence and regularity of the global attractor for a weakly damped forced shallow water equation in  . Tian et al.[48] studied the global attractor for the viscous weakly damped forced Korteweg-de Vries equations in
. Tian et al.[48] studied the global attractor for the viscous weakly damped forced Korteweg-de Vries equations in  . Yanhong Zhang and Chengkui Zhong [49] investigated the existence of global attractors for a nonlinear wave equation. Lixin Tian and Ruihua Tian [50] studied the attractor for the two-dimensional weakly damped KdV equation in belt field. Ying Xu and Lixin Tian [51] investigated attractor for a coupled nonhomogeneous Camassa-Holm equation with periodic boundary condition. Lixin Tian and Jinglin Fan [52] discussed the global attractors for the viscous Degasperis-Procesi equation in
. Yanhong Zhang and Chengkui Zhong [49] investigated the existence of global attractors for a nonlinear wave equation. Lixin Tian and Ruihua Tian [50] studied the attractor for the two-dimensional weakly damped KdV equation in belt field. Ying Xu and Lixin Tian [51] investigated attractor for a coupled nonhomogeneous Camassa-Holm equation with periodic boundary condition. Lixin Tian and Jinglin Fan [52] discussed the global attractors for the viscous Degasperis-Procesi equation in  . Lixin Tian and Ying Gao [53] obtained global attractors for the viscous Fornberg-Whitham equation [54] in
. Lixin Tian and Ying Gao [53] obtained global attractors for the viscous Fornberg-Whitham equation [54] in  . Here we investigate the existence of global attractor for a viscous coupled Camassa-Holm equation with the periodic boundary condition in
. Here we investigate the existence of global attractor for a viscous coupled Camassa-Holm equation with the periodic boundary condition in  as follows:
as follows:





where  . To the authors' knowledge, the problem of global attractor for (1.9)–(1.13) has not been discussed in previous publications.
. To the authors' knowledge, the problem of global attractor for (1.9)–(1.13) has not been discussed in previous publications.
Our paper is organized as follows. In Section 2, we give the main definitions and Lemmas. In Section 3, main results are presented, as the core of the paper, and the proofs of the main theorems are completed. Firstly, we prove that (1.9)–(1.13) has a unique solution in infinite time interval then obtain the existence of global solution of (1.9)–(1.13) in  by prior estimates. Meanwhile we obtain that the semigroup of the solution operator has an absorbing set. Finally, we demonstrate the long-time behavior of solution of (1.9)–(1.13) that is described by global attractor. In brief, we obtain the existence of the global attractor for (1.9)–(1.13) in
by prior estimates. Meanwhile we obtain that the semigroup of the solution operator has an absorbing set. Finally, we demonstrate the long-time behavior of solution of (1.9)–(1.13) that is described by global attractor. In brief, we obtain the existence of the global attractor for (1.9)–(1.13) in  .
.
2. Preliminaries
Definition 2.1.
Let
 stand for the
stand for the
 inner product and
inner product and
 the corresponding
the corresponding
 norm. one also denotes
norm. one also denotes

and  where
where  is Laplace operators and
is Laplace operators and  is a self-adjoint positive operators with compact inverse. The eigenvalue of
is a self-adjoint positive operators with compact inverse. The eigenvalue of  is
is  satisfying
satisfying  as
as  , where
, where  is the corresponding eigenvector of
is the corresponding eigenvector of  . For simplicity we will give the following inequalities and only refer to their names wherever necessary.
. For simplicity we will give the following inequalities and only refer to their names wherever necessary.
Lemma 2.2 (consistent Gronwall inequality).
Assume that  are three positive locally integrable functions defined on
are three positive locally integrable functions defined on  is a locally integrable function over
is a locally integrable function over  , satisfying
, satisfying

where  are positive constants. one can get
are positive constants. one can get

Lemma 2.3 (Sobolev inequality).
Suppose that  and there exists a constant c, such that
and there exists a constant c, such that

Lemma 2.4 (Young inequality).
 where
where  As p = q = 2, one has
As p = q = 2, one has 
3. Main Results and the Proof of the Theorems
Based on Galerkin procedure, we will show the existence of global solution of (1.9)–(1.13). Suppose that  is an orthonormal basis in the space
is an orthonormal basis in the space  consisting of eigenfunctions of the operator
consisting of eigenfunctions of the operator  .
.  ,
,  is orthogonal projection from
is orthogonal projection from  to
to  . By Galerkin procedure [55], (1.9)–(1.13) can be reduced to ordinary differential system
. By Galerkin procedure [55], (1.9)–(1.13) can be reduced to ordinary differential system



By means of existence theory of solution to ordinary differential equations, we know that local smooth solution of (3.1)–(3.3) exists. Now we can establish consistent integral estimate on approximate solution with respect to  by Galerkin method.
by Galerkin method.
Theorem 3.1.
If  ,
,  then (1.9)–(1.13) has a global solution in
then (1.9)–(1.13) has a global solution in  .
.
Proof.
Taking the inner product of (3.1), and (3.2), respectively, with  in
in  and noting that
and noting that



with the same reason, we obtain that

By integrating by parts we get

From (3.4) and (3.5) we obtain that

Applying Poincaré inequality, we get

Equality (3.9) implies that


where  is nonnegative constant.
is nonnegative constant.
Integrating (3.9) over  yields
yields

Taking the inner product of (3.1) and (3.2), respectively, with  in
in  , we get
, we get


since

By means of integrating by parts frequently, we obtain that

Associating all the above inequalities leads to

Simplifying the above inequality and employing Young inequality, it follows that

where  . By means of Poincaré inequality, we obtain that
. By means of Poincaré inequality, we obtain that

Let

from (3.13) we get

Finally we obtain that

Integrating (3.19) over  yields
yields

where  are positive constants.
are positive constants.
Taking the inner product of (3.1) and (3.2), respectively, with  , in
, in  , we obtain that
, we obtain that

By integrating by parts and applying Sobolev inequality, we obtain that

where  is a constant depending on
is a constant depending on  As well as
As well as

where  is a constant depending on
is a constant depending on  Combining all the above inequalities, we have
Combining all the above inequalities, we have

By employing Young inequality, it follows that

where  Based on Poincaré inequality we obtain that
Based on Poincaré inequality we obtain that

Let

from (3.12) and (3.23), we conclude that  is bounded, so we suppose that
is bounded, so we suppose that  ; by (3.24), we have
; by (3.24), we have

Using Gronwall inequality, we obtain that

Integrating (3.29) over  , we obtain that
, we obtain that

where  are nonnegative constants.
are nonnegative constants.
Respectively, taking the inner product of (3.1) and (3.2) with  in
in  , we can also get
, we can also get  . Connecting (3.12) and (3.23) with (3.33), we can get that
. Connecting (3.12) and (3.23) with (3.33), we can get that

so  are bounded.
are bounded.
Then we get that 
 are bounded. Considering Aubin's compactness theorem, we conclude that there is a subsequence
are bounded. Considering Aubin's compactness theorem, we conclude that there is a subsequence  ,
, ,
, ,
, , so that
, so that  ,
, ,
, , and
, and  Now we replace
Now we replace  with
with  . We will prove that
. We will prove that  satisfy (1.9)–(1.10). That is to say, approximate solution of (3.1)–(3.2) is convergent to solution of (1.9)–(1.10).
satisfy (1.9)–(1.10). That is to say, approximate solution of (3.1)–(3.2) is convergent to solution of (1.9)–(1.10).
Let  is finite from the above discussion, and by ordinary differential equation (3.1), we have
is finite from the above discussion, and by ordinary differential equation (3.1), we have

Now it is clear that

Note that

From the above statements we get

Similarly, we have that

For all  , we obtain that
, we obtain that

From ordinary differential equation (3.2), we know that

as we know that

From the above discussions we get

Simultaneously, we have that

For all  , we obtain
, we obtain

All the above analysis shows that the global solution to (1.9)–(1.13) exists in  .
.
Theorem 3.2.
Denote  as the semigroup of the solution operator to (1.9)–(1.13),
as the semigroup of the solution operator to (1.9)–(1.13),  Then
Then  has an absorbing set in
has an absorbing set in 
Proof.
Taking the inner product of (1.9) and (1.10),respectively, with  in
in  , noting that
, noting that

and associating with all the above statements, we obtain

According to the Poincaré inequality, we obtain that

where  is nonnegative constant.
is nonnegative constant.
Integrating (3.48) over  , we obtain that
, we obtain that

We will obtain the uniform estimate of (1.9)–(1.13) in  as follows.
as follows.
Taking the inner product of (1.9) and (1.10), respectively, with  , we have
, we have

we also obtain

From all the previous statements we obtain that

where  . From Poincaré inequality, we get
. From Poincaré inequality, we get

Let

From (3.50) we have that

Integrating (3.53) over  , it follows that
, it follows that

where  are nonnegative constants. Taking the inner product of (1.9) and (1.10), respectively, with
are nonnegative constants. Taking the inner product of (1.9) and (1.10), respectively, with  , we have that
, we have that

Integrating by parts and employing Sobolev inequality, we get

where  is a constant depending on
is a constant depending on 

where  is a constant depending on
is a constant depending on  From all the above inequalities we obtain that
From all the above inequalities we obtain that

Then it follows that

where  By means of Poincaré inequality, we obtain that
By means of Poincaré inequality, we obtain that

Let

from (3.49) and (3.56), we conclude that  is bounded; assume that
is bounded; assume that  . From (3.57), we have
. From (3.57), we have

Then through Gronwall inequality, we obtain

Integrating (3.62) on  , we have that
, we have that

where  are nonnegative constants. Then from (3.66), we can get
are nonnegative constants. Then from (3.66), we can get  In other words, open ball
In other words, open ball  is the attracting set of
is the attracting set of  in
in  .
.
Theorem 3.3.
Suppose that  then the semigroup of the solution operator
then the semigroup of the solution operator  to (1.9)–(1.13) has a global attractor in
to (1.9)–(1.13) has a global attractor in 
Proof.
To obtain the existence of the global attractor, we will prove that it is a compact operator. Taking inner product of (1.9) and (1.10) with  in
in  , we obtain
, we obtain


By integrating by parts, we obtain that

Similarly, we obtain

where  is a constant depending on
is a constant depending on  Integrating by parts frequently, we obtain
Integrating by parts frequently, we obtain

From (3.68) and (3.69), we know that

where  Employing Young inequality, we obtain that
Employing Young inequality, we obtain that

where  . From Poincaré inequality, we obtain that
. From Poincaré inequality, we obtain that

Let

Through (3.67), we have

We also get

Through (3.49), (3.56), and (3.66), we assume that

Then we have

and all the analysis indicates that

Finally we obtain that

We know that the injection of  into
into  is compact, then we can conclude that
is compact, then we can conclude that  is equi-continuity. From Ascoli-Arzela's theorem, we know that
is equi-continuity. From Ascoli-Arzela's theorem, we know that  has the global attractor in
has the global attractor in  .
.
References
Fuchssteiner B, Fokas AS: Symplectic structures, their Bäcklund transformations and hereditary symmetries. Physica D 1981,4(1):47-66. 10.1016/0167-2789(81)90004-X
Camassa R, Holm DD: An integrable shallow water equation with peaked solitons. Physical Review Letters 1993,71(11):1661-1664. 10.1103/PhysRevLett.71.1661
Camassa R, Holm DD, Hyman JM: A new integrable shallow water equation. Advances in Applied Mechanics 1994, 31: 1-33.
Whitham GB: Linear and Nonlinear Waves, Pure and Applied Mathematic. John Wiley & Sons, New York, NY, USA; 1974:xvi+636.
Constantin A, Strauss WA: Stability of peakons. Communications on Pure and Applied Mathematics 2000,53(5):603-610. 10.1002/(SICI)1097-0312(200005)53:5<603::AID-CPA3>3.0.CO;2-L
Constantin A, Molinet L: Orbital stability of solitary waves for a shallow water equation. Physica D 2001,157(1-2):75-89. 10.1016/S0167-2789(01)00298-6
Constantin A, Escher J: Particle trajectories in solitary water waves. Bulletin of American Mathematical Society 2007,44(3):423-431. 10.1090/S0273-0979-07-01159-7
Constantin A: The trajectories of particles in Stokes waves. Inventiones Mathematicae 2006,166(3):523-535. 10.1007/s00222-006-0002-5
Constantin A, Escher J: Wave breaking for nonlinear nonlocal shallow water equations. Acta Mathematica 1998,181(2):229-243. 10.1007/BF02392586
Constantin A, Strauss WA: Stability of a class of solitary waves in compressible elastic rods. Physics Letters A 2000,270(3-4):140-148. 10.1016/S0375-9601(00)00255-3
Dai H-H: Model equations for nonlinear dispersive waves in a compressible Mooney-Rivlin rod. Acta Mechanica 1998,127(1–4):193-207.
Bressan A, Constantin A: Global conservative solutions of the Camassa-Holm equation. Archive for Rational Mechanics and Analysis 2007,183(2):215-239. 10.1007/s00205-006-0010-z
Bressan A, Constantin A: Global dissipative solutions of the Camassa-Holm equation. Analysis and Applications 2007,5(1):1-27. 10.1142/S0219530507000857
Parker A: Wave dynamics for peaked solitons of the Camassa-Holm equation. Chaos, Solitons and Fractals 2008,35(2):220-237. 10.1016/j.chaos.2007.07.049
Beals R, Sattinger DH, Szmigielski J: Multipeakons and the classical moment problem. Advances in Mathematics 2000,154(2):229-257. 10.1006/aima.1999.1883
Beals R, Sattinger DH, Szmigielski J: Multi-peakons and a theorem of Stieltjes. Inverse Problems 1999,15(1):L1-L4. 10.1088/0266-5611/15/1/001
Constantin A, Johnson RS: Propagation of very long water waves, with vorticity, over variable depth, with applications to tsunamis. Fluid Dynamics Research 2008,40(3):175-211. 10.1016/j.fluiddyn.2007.06.004
Holden H, Raynaud X: Global conservative solutions of the Camassa-Holm equation—a Lagrangian point of view. Communications in Partial Differential Equations 2007,32(10–12):1511-1549.
Constantin A: On the Cauchy problem for the periodic Camassa-Holm equation. Journal of Differential Equations 1997,141(2):218-235. 10.1006/jdeq.1997.3333
Constantin A: On the inverse spectral problem for the Camassa-Holm equation. Journal of Functional Analysis 1998,155(2):352-363. 10.1006/jfan.1997.3231
Constantin A, Gerdjikov VS, Ivanov RI: Inverse scattering transform for the Camassa-Holm equation. Inverse Problems 2006,22(6):2197-2207. 10.1088/0266-5611/22/6/017
Rui W, He B, Long Y, Chen C: The integral bifurcation method and its application for solving a family of third-order dispersive PDEs. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1256-1267. 10.1016/j.na.2007.06.027
Rui W, Xie S, Long Y, He B: Integral bifurcation method and its application for solving the modified equal width wave equation and its variants. Rostocker Mathematisches Kolloquium 2007, (62):87-106.
Lenells J: Infinite propagation speed of the Camassa-Holm equation. Journal of Mathematical Analysis and Applications 2007,325(2):1468-1478. 10.1016/j.jmaa.2006.02.045
Cohen D, Owren B, Raynaud X: Multi-symplectic integration of the Camassa-Holm equation. Journal of Computational Physics 2008,227(11):5492-5512. 10.1016/j.jcp.2008.01.051
Meng Y, Tian L: Boundary control of the viscous generalized Camassa-Holm equation. International Journal of Nonlinear Science 2009,8(2):173-181.
Long Y, Li Z, Rui W: New travelling wave solutions for a nonlinearly dispersive wave equation of Camassa-Holm equation type. Applied Mathematics and Computation 2010,217(4):1315-1320. 10.1016/j.amc.2009.04.083
Rui W-G, Long Y: New periodic loop solitons of the generalized KdV equation. International Journal of Nonlinear Sciences and Numerical Simulation 2008,9(4):441-444. 10.1515/IJNSNS.2008.9.4.441
Ding DP, Tian LX: The attractor on dissipative Camassa-Holm equation. Acta Mathematicae Applicatae Sinica 2004,27(3):536-545.
Ding D, Tian L: The study of solution of dissipative Camassa-Holm equation on total space. International Journal of Nonlinear Science 2006,1(1):37-42.
Olson EA: Well posedness for a higher order modified Camassa-Holm equation. Journal of Differential Equations 2009,246(10):4154-4172. 10.1016/j.jde.2008.12.001
Zhou J, Tian L: Blow-up of solution of an initial boundary value problem for a generalized Camassa-Holm equation. Physics Letters A 2008,372(20):3659-3666. 10.1016/j.physleta.2008.02.032
Tian L, Shen C, Ding D: Optimal control of the viscous Camassa-Holm equation. Nonlinear Analysis: Real World Applications 2009,10(1):519-530. 10.1016/j.nonrwa.2007.10.016
Tian L, Gui G, Liu Y: On the well-posedness problem and the scattering problem for the Dullin-Gottwald-Holm equation. Communications in Mathematical Physics 2005,257(3):667-701. 10.1007/s00220-005-1356-z
Chen M, Liu S-Q, Zhang Y: A two-component generalization of the Camassa-Holm equation and its solutions. Letters in Mathematical Physics 2006,75(1):1-15. 10.1007/s11005-005-0041-7
Constantin A, Ivanov RI: On an integrable two-component Camassa-Holm shallow water system. Physics Letters A 2008,372(48):7129-7132. 10.1016/j.physleta.2008.10.050
Popowicz Z: A two-component generalization of the Degasperis-Procesi equation. Journal of Physics A 2006,39(44):13717-13726. 10.1088/0305-4470/39/44/007
Henry D: Infinite propagation speed for a two component Camassa-Holm equation. Discrete and Continuous Dynamical Systems. Series B 2009,12(3):597-606.
Escher J, Lechtenfeld O, Yin ZY: Well-posedness and blow-up phenomena for the twocomponent Camassa-Holm equation. Discrete and Continuous Dynamical Systems 2007,19(3):493-513.
Guan C, Yin Z: Global existence and blow-up phenomena for an integrable two-component Camassa-Holm shallow water system. Journal of Differential Equations 2010,248(8):2003-2014. 10.1016/j.jde.2009.08.002
Li JB, Li YS: Bifurcations of travelling wave solutions for a two-component Camassa-Holm equation. Acta Mathematica Sinica 2008,24(8):1319-1330. 10.1007/s10114-008-6207-3
Wang Y, Huang J, Chen L: Global conservative solutions of the two-component Camassa-Holm shallow water system. International Journal of Nonlinear Science 2010, 9: 379-384.
Aratyn H, Gomes JF, Zimerman AH:Deformations of
 superconformal algebra and supersymmetric two-component Camassa-Holm equation. Journal of Physics A 2007,40(17):4511-4527. 10.1088/1751-8113/40/17/008
superconformal algebra and supersymmetric two-component Camassa-Holm equation. Journal of Physics A 2007,40(17):4511-4527. 10.1088/1751-8113/40/17/008Constantin A, Kolev B: Geodesic flow on the diffeomorphism group of the circle. Commentarii Mathematici Helvetici 2003,78(4):787-804. 10.1007/s00014-003-0785-6
Constantin A: Existence of permanent and breaking waves for a shallow water equation: a geometric approach. Annales de l'Institut Fourier 2000,50(2):321-362. 10.5802/aif.1757
Fu Y, Qu C: Well posedness and blow-up solution for a new coupled Camassa-Holm equations with peakons. Journal of Mathematical Physics 2009,50(1):-25.
Li Y, Yang X:Existence and regularity of the global attractor for a weakly damped forced shallow water equation in
 . Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5587-5598. 10.1016/j.na.2009.04.056
. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5587-5598. 10.1016/j.na.2009.04.056Tian L, Tian R, Fan J:The global attractor for the viscous weakly damped forced Korteweg-de Vries equations in
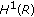 . International Journal of Nonlinear Science 2008,5(1):3-10.
. International Journal of Nonlinear Science 2008,5(1):3-10.Zhang Y, Zhong C: Existence of global attractors for a nonlinear wave equation. Applied Mathematics Letters 2005,18(1):77-84. 10.1016/j.aml.2004.08.002
Tian L, Tian R: The attractor for the two-dimensional weakly damped KdV equation in belt field. Nonlinear Analysis: Real World Applications 2008,9(3):912-919. 10.1016/j.nonrwa.2007.01.009
Xu Y, Tian L: Attractor for a coupled nonhomogeneous Camassa-Holm equation. International Journal of Nonlinear Science 2010, 9: 112-117.
Tian L, Fan J: The attractor on viscosity Degasperis-Procesi equation. Nonlinear Analysis: Real World Applications 2007,9(4):1461-1473.
Tian L, Gao Y: The global attractor of the viscous Fornberg-Whitham equation. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5176-5186. 10.1016/j.na.2009.04.004
Zhou J, Tian L: A type of bounded traveling wave solutions for the Fornberg-Whitham equation. Journal of Mathematical Analysis and Applications 2008,346(1):255-261. 10.1016/j.jmaa.2008.05.055
Guo BL: Infinite Dimensional Dynamical System. 1st edition. , Beijing, China; 2000.
Acknowledgments
The authors really appreciate Professor Yue Liu for his valuable comments and opinions. The paper is supported by the National Nature Science Foundation of China (no. 10771088) and Nature Science Foundation of Jiangsu(no. BK 2010329) and Outstanding Personnel Program in Six Fields of Jiangsu (no. 6-A-029).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tian, L., Xu, Y. Attractor for a Viscous Coupled Camassa-Holm Equation. Adv Differ Equ 2010, 512812 (2010). https://doi.org/10.1155/2010/512812
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/512812
 superconformal algebra and supersymmetric two-component Camassa-Holm equation. Journal of Physics A 2007,40(17):4511-4527. 10.1088/1751-8113/40/17/008
superconformal algebra and supersymmetric two-component Camassa-Holm equation. Journal of Physics A 2007,40(17):4511-4527. 10.1088/1751-8113/40/17/008 . Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5587-5598. 10.1016/j.na.2009.04.056
. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5587-5598. 10.1016/j.na.2009.04.056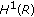 . International Journal of Nonlinear Science 2008,5(1):3-10.
. International Journal of Nonlinear Science 2008,5(1):3-10.