- Research Article
- Open access
- Published:
Monotone Iterative Technique for First-Order Nonlinear Periodic Boundary Value Problems on Time Scales
Advances in Difference Equations volume 2010, Article number: 620459 (2010)
Abstract
We investigate the following nonlinear first-order periodic boundary value problem on time scales:  ,
,  ,
,  . Some new existence criteria of positive solutions are established by using the monotone iterative technique.
. Some new existence criteria of positive solutions are established by using the monotone iterative technique.
1. Introduction
Recently, periodic boundary value problems (PBVPs for short) for dynamic equations on time scales have been studied by several authors by using the method of lower and upper solutions, fixed point theorems, and the theory of fixed point index. We refer the reader to [1–10] for some recent results.
In this paper we are interested in the existence of positive solutions for the following first-order PBVP on time scales:

where  will be defined in Section 2,
will be defined in Section 2,  is a time scale,
is a time scale,  is fixed and
is fixed and 
 . For each interval
. For each interval  of
of  we denote by
we denote by  By applying the monotone iterative technique, we obtain not only the existence of positive solution for the PBVP (1.1), but also give an iterative scheme, which approximates the solution. It is worth mentioning that the initial term of our iterative scheme is a constant function, which implies that the iterative scheme is significant and feasible. For abstract monotone iterative technique, see [11] and the references therein.
By applying the monotone iterative technique, we obtain not only the existence of positive solution for the PBVP (1.1), but also give an iterative scheme, which approximates the solution. It is worth mentioning that the initial term of our iterative scheme is a constant function, which implies that the iterative scheme is significant and feasible. For abstract monotone iterative technique, see [11] and the references therein.
2. Some Results on Time Scales
Let us recall some basic definitions and relevant results of calculus on time scales [12–15].
Definition 2.1.
For  we define the forward jump operator
we define the forward jump operator  by
by

while the backward jump operator  is defined by
is defined by

In this definition we put  and
and  where
where  denotes the empty set
denotes the empty set If
If  we say that
we say that  is right scattered, while if
is right scattered, while if  we say that
we say that  is left scattered. Also, if
is left scattered. Also, if  and
and  then
then  is called right dense, and if
is called right dense, and if  and
and  then
then  is called left dense. We also need below the set
is called left dense. We also need below the set  which is derived from the time scale
which is derived from the time scale  as follows. If
as follows. If  has a left-scattered maximum
has a left-scattered maximum  then
then  Otherwise,
Otherwise, 
Definition 2.2.
Assume that  is a function and let
is a function and let  Then
Then  is called differentiable at
is called differentiable at  if there exists a
if there exists a  such that, for any given
such that, for any given  there is an open neighborhood
there is an open neighborhood  of
of  such that
such that

In this case,  is called the delta derivative of
is called the delta derivative of  at
at  and we denote it by
and we denote it by  If
If  then we define the integral by
then we define the integral by

Definition 2.3.
A function  is called rd-continuous provided that it is continuous at right-dense points in
is called rd-continuous provided that it is continuous at right-dense points in  and its left-sided limits exist at left-dense points in
and its left-sided limits exist at left-dense points in  The set of rd-continuous functions
The set of rd-continuous functions  will be denoted by
will be denoted by 
Lemma 2.4 (see [13]).
If  and
and  then
then

where  is the graininess function.
is the graininess function.
Lemma 2.5 (see [13]).
If  then
then  is increasing.
is increasing.
Definition 2.6.
For  we define the Hilger complex numbers as
we define the Hilger complex numbers as

and for  let
let 
Definition 2.7.
For  let
let  be the strip
be the strip

and for  let
let 
Definition 2.8.
For  we define the cylinder transformation
we define the cylinder transformation  by
by

where  is the principal logarithm function. For
is the principal logarithm function. For  we define
we define  for all
for all 
Definition 2.9.
A function  is regressive provided that
is regressive provided that

The set of all regressive and rd-continuous functions will be denoted by 
Definition 2.10.
We define the set  of all positively regressive elements of
of all positively regressive elements of  by
by

Definition 2.11.
If  , then the generalized exponential function is given by
, then the generalized exponential function is given by

where the cylinder transformation  is defined as in Definition 2.8.
is defined as in Definition 2.8.
Lemma 2.12 (see [13]).
If  , then
, then
-
(i)
 ,
, -
(ii)
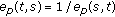 ,
, -
(iii)
 ,
, -
(iv)
 for
for  and
and 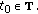
Lemma 2.13 (see [13]).
If  and
and  , then
, then

3. Main Results
For the forthcoming analysis, we assume that the following two conditions are satisfied.
(H1) is rd-continuous, which implies that
is rd-continuous, which implies that  .
.
(H2) is continuous and
is continuous and  is nondecreasing on
is nondecreasing on  .
.
If we denote that

then we may claim that  , which implies that
, which implies that 
In fact, in view of (H1) and Lemmas 2.12 and 2.13, we have

which together with Lemma 2.5 shows that  is increasing on
is increasing on  And so,
And so,

This indicates that  .
.
Let

be equipped with the norm  Then
Then  is a Banach space.
is a Banach space.
First, we define two cones  and
and  in
in  as follows:
as follows:

and then we define an operator 

It is obvious that fixed points of  are solutions of the PBVP (1.1).
are solutions of the PBVP (1.1).
Since  is nondecreasing on
is nondecreasing on  , we have the following lemma.
, we have the following lemma.
Lemma 3.1.
 is nondecreasing.
is nondecreasing.
Lemma 3.2.
 is completely continuous.
is completely continuous.
Proof.
Suppose that  Then
Then

so,

Therefore,

This shows that  . Furthermore, with similar arguments as in [7], we can prove that
. Furthermore, with similar arguments as in [7], we can prove that  is completely continuous by Arzela-Ascoli theorem.
is completely continuous by Arzela-Ascoli theorem.
Theorem 3.3.
Assume that there exist two positive numbers  such that
such that

Then the PBVP (1.1) has positive solutions  and
and  , which may coincide with
, which may coincide with

where  and
and  for
for  .
.
Proof.
First, we define

Then we may assert that

In fact, if  , then
, then

which together with (H2) and (3.10) implies that

which shows that

Now, if we denote that  for
for  , then
, then  . Let
. Let

In view of  , we have
, we have  Since the set
Since the set  is bounded and the operator
is bounded and the operator  is compact, we know that the set
is compact, we know that the set  is relatively compact, which implies that there exists a subsequence
is relatively compact, which implies that there exists a subsequence  such that
such that

Moreover, since

it follows from Lemma 3.1 that  ; that is,
; that is,  . By induction, it is easy to know that
. By induction, it is easy to know that

which together with (3.18) implies that

Since  is continuous, it follows from (3.17) and (3.21) that
is continuous, it follows from (3.17) and (3.21) that

which shows that  is a solution of the PBVP (1.1). Furthermore, we get from
is a solution of the PBVP (1.1). Furthermore, we get from  that
that

On the other hand, if we denote that  for
for  and that
and that  then we can obtain similarly that
then we can obtain similarly that  and there exists a subsequence
and there exists a subsequence  such that
such that

Moreover, since

it is also easy to know that

With the similar arguments as above, we can prove that  is a solution of the PBVP (1.1) and satisfies
is a solution of the PBVP (1.1) and satisfies

Corollary 3.4.
If the following conditions are fulfilled:

then there exist two positive numbers  such that (3.10) is satisfied, which implies that the PBVP (1.1) has positive solutions
such that (3.10) is satisfied, which implies that the PBVP (1.1) has positive solutions  and
and  , which may coincide with
, which may coincide with

where  and
and  for
for  .
.
Example 3.5.
Let  We consider the following PBVP on
We consider the following PBVP on  :
:

Since 
 and
and  we can obtain that
we can obtain that

Thus, if we choose  and
and  , then all the conditions of Theorem 3.3 are fulfilled. So, the PBVP (3.30) has positive solutions
, then all the conditions of Theorem 3.3 are fulfilled. So, the PBVP (3.30) has positive solutions  and
and  , which may coincide with
, which may coincide with

where  and
and  for
for  .
.
References
Cabada A: Extremal solutions and Green's functions of higher order periodic boundary value problems in time scales. Journal of Mathematical Analysis and Applications 2004,290(1):35-54. 10.1016/j.jmaa.2003.08.018
Dai Q, Tisdell CC: Existence of solutions to first-order dynamic boundary value problems. International Journal of Difference Equations 2006,1(1):1-17.
Eloe PW: The method of quasilinearization and dynamic equations on compact measure chains. Journal of Computational and Applied Mathematics 2002,141(1-2):159-167. 10.1016/S0377-0427(01)00443-5
Topal SG: Second-order periodic boundary value problems on time scales. Computers & Mathematics with Applications 2004,48(3-4):637-648. 10.1016/j.camwa.2002.04.005
Stehlík P: Periodic boundary value problems on time scales. Advances in Difference Equations 2005, 1: 81-92. 10.1155/ADE.2005.81
Sun J-P, Li W-T: Positive solution for system of nonlinear first-order PBVPs on time scales. Nonlinear Analysis: Theory, Methods & Applications 2005,62(1):131-139. 10.1016/j.na.2005.03.016
Sun J-P, Li W-T: Existence of solutions to nonlinear first-order PBVPs on time scales. Nonlinear Analysis: Theory, Methods & Applications 2007,67(3):883-888. 10.1016/j.na.2006.06.046
Sun J-P, Li W-T: Existence and multiplicity of positive solutions to nonlinear first-order PBVPs on time scales. Computers & Mathematics with Applications 2007,54(6):861-871. 10.1016/j.camwa.2007.03.009
Sun J-P, Li W-T: Positive solutions to nonlinear first-order PBVPs with parameter on time scales. Nonlinear Analysis: Theory, Methods & Applications 2009,70(3):1133-1145. 10.1016/j.na.2008.02.007
Wu S-T, Tsai L-Y: Periodic solutions for dynamic equations on time scales. Tamkang Journal of Mathematics 2009,40(2):173-191.
Ahmad B, Nieto JJ:The monotone iterative technique for three-point second-order integrodifferential boundary value problems with
 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.Agarwal RP, Bohner M: Basic calculus on time scales and some of its applications. Results in Mathematics 1999,35(1-2):3-22.
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Hilger S: Analysis on measure chains—a unified approach to continuous and discrete calculus. Results in Mathematics 1990,18(1-2):18-56.
Kaymakcalan B, Lakshmikantham V, Sivasundaram S: Dynamic Systems on Measure Chains, Mathematics and Its Applications. Volume 370. Kluwer Academic Publishers, Boston, Mass, USA; 1996:x+285.
Acknowledgment
This work was supported by the National Natural Science Foundation of China (10801068).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhao, YH., Sun, JP. Monotone Iterative Technique for First-Order Nonlinear Periodic Boundary Value Problems on Time Scales. Adv Differ Equ 2010, 620459 (2010). https://doi.org/10.1155/2010/620459
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/620459
 ,
,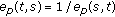 ,
, ,
, for
for  and
and 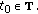
 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.