- Research Article
- Open access
- Published:
Approximate Controllability of Abstract Discrete-Time Systems
Advances in Difference Equations volume 2010, Article number: 695290 (2010)
Abstract
Approximate controllability for semilinear abstract discrete-time systems is considered. Specifically, we consider the semilinear discrete-time system  ,
,  , where
, where  are bounded linear operators acting on a Hilbert space
are bounded linear operators acting on a Hilbert space  ,
,  are
are  -valued bounded linear operators defined on a Hilbert space
-valued bounded linear operators defined on a Hilbert space  , and
, and  is a nonlinear function. Assuming appropriate conditions, we will show that the approximate controllability of the associated linear system
is a nonlinear function. Assuming appropriate conditions, we will show that the approximate controllability of the associated linear system  implies the approximate controllability of the semilinear system.
implies the approximate controllability of the semilinear system.
1. Introduction
In this paper we deal with the controllability problem for semilinear distributed discrete-time control systems. In order to specify the class of systems to be considered, we set  for the state space and
for the state space and  for the control space. We assume that
for the control space. We assume that  and
and  are Hilbert spaces. Moreover, throughout this paper we denote by
are Hilbert spaces. Moreover, throughout this paper we denote by  bounded linear operators,
bounded linear operators,  ,
,  , bounded linear maps that represent the control action, and
, bounded linear maps that represent the control action, and  a map such that
a map such that  is continuous for each
is continuous for each  . Furthermore,
. Furthermore,  , and
, and  satisfy appropriate conditions which will be specified later. We will study the controllability of control systems described by the equation
satisfy appropriate conditions which will be specified later. We will study the controllability of control systems described by the equation

where  ,
,  .
.
The study of controllability is an important topic in systems theory. In particular, the controllability of systems similar to (1.1) has been the object of several works. We only mention here [1–11] and the references cited therein. Specially, Leiva and Uzcategui [5] have studied the exact controllability of the linear and semilinear system. However, it is well known [12–16] that most of continuous distributed systems that arise in concrete situations are not exactly controllable but only approximately controllable. A similar situation has been established in [10] in relation with the discrete wave equation and in [11] in relation with the discrete heat equation (see [17–22]). As mentioned in this paper, the lack of controllability is related to the fact that the spaces in which the solutions of these systems evolve are infinite dimensional.
For this reason, in this paper we study the approximate controllability of system (1.1). Specifically, we will compare the approximate controllability of system (1.1) with the approximate controllability of linear system

where  and
and  .
.
Throughout this paper, for Hilbert spaces  ,
,  , we denote by
, we denote by  the Banach space of bounded linear operators from
the Banach space of bounded linear operators from  into
into  , and we abbreviate this notation by
, and we abbreviate this notation by  for
for  . Moreover, for a linear operator
. Moreover, for a linear operator  we denote by
we denote by  the range space of
the range space of  .
.
The following property of Hilbert spaces is essential for our treatment of controllability.
Lemma 1.1.
Let  be a Hilbert space, and let
be a Hilbert space, and let  be closed subspaces of
be closed subspaces of  such that
such that  . Then there exists a bounded linear projection
. Then there exists a bounded linear projection  such that for each
such that for each  ,
,  and
and

In the next section we study the controllability of systems of type (1.1) when the state space  is a Hilbert space and, in Section 3, we will apply our results to study the controllability of a typical system.
is a Hilbert space and, in Section 3, we will apply our results to study the controllability of a typical system.
2. Approximate Controllability
Throughout this section, we assume that  and
and  are Hilbert spaces endowed with an inner product denoted generically by
are Hilbert spaces endowed with an inner product denoted generically by  . In this case, for
. In this case, for  ,
,  and
and  are also Hilbert spaces. The inner product in
are also Hilbert spaces. The inner product in  is given by
is given by  for
for  ,
,  , and similarly for
, and similarly for  .
.
Let  be the evolution operator associated to the linear homogeneous equation
be the evolution operator associated to the linear homogeneous equation


Furthermore, the solution of (1.2) is given by

We will abbreviate the notation by writing  for this solution.
for this solution.
We define the bounded linear operator  by
by

It is clear that  .
.
The system (1.2) is said to be exactly controllable (or simply controllable) on  if
if  .
.
Definition 2.1.
System (1.2) is said to be approximately controllable on  if the space
if the space  is dense in
is dense in  and approximately controllable in finite time if the space
and approximately controllable in finite time if the space  is dense in
is dense in  .
.
If the system (1.2) is approximately controllable on  and
and  is a finite-dimensional space, then the system (1.2) is controllable on
is a finite-dimensional space, then the system (1.2) is controllable on  .
.
We introduce the reachability set  of system (1.2) as the set consisting of the values
of system (1.2) as the set consisting of the values  . Clearly, system (1.2) is approximately controllable on
. Clearly, system (1.2) is approximately controllable on  if and only if
if and only if  is dense in
is dense in  for every
for every  . A weaker property of controllability is established in the following definition.
. A weaker property of controllability is established in the following definition.
Definition 2.2.
System (1.2) is said to be approximately controllable to the origin on  if
if  for every
for every  and approximately controllable to the origin in finite time if
and approximately controllable to the origin in finite time if  for every
for every  .
.
On the other hand, for  , (1.1) has a unique solution which satisfies the equation
, (1.1) has a unique solution which satisfies the equation

Proceeding as in Definitions 2.1 and 2.2, we next consider the approximate controllability for system (1.1). Let  be the solution of (1.1) with initial condition
be the solution of (1.1) with initial condition  and control function
and control function  . We introduce the reachability set
. We introduce the reachability set  of system (1.1) as the set consisting of the values
of system (1.1) as the set consisting of the values  .
.
Definition 2.3.
System (1.1) is said to be
-
(a)
approximately controllable on
 if
if  is dense in
is dense in 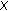 ,
, -
(b)
approximately controllable in finite time if
 is dense in
is dense in 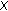 ,
, -
(c)
approximately controllable to the origin on
 if
if 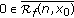 for every
for every 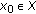 ,
, -
(d)
approximately controllable to the origin in finite time if
 for every
for every 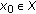 .
.
We next introduce some additional notations. The operators  and
and  are given by
are given by

It is clear that  and
and  are bounded linear operators. We set
are bounded linear operators. We set  . Moreover, we denote by
. Moreover, we denote by  the operator defined by
the operator defined by  .
.
We denote by  the space consisting of
the space consisting of  such that
such that  .
.
Next we will show that a modification of an argument of Sukavanam [23] can be applied to compare the approximate controllability of systems (1.1) and (1.2).
For fixed  and
and  , we begin by defining the map
, we begin by defining the map  by
by  . It is clear that
. It is clear that  is a continuous map.
is a continuous map.
On the other hand, under the assumption that

we denote by  the projection constructed as in Lemma 1.1 with
the projection constructed as in Lemma 1.1 with  and
and  . We introduce the space
. We introduce the space

and we define the map  by
by

We next study the existence of fixed points for  . In the following statement, we denote
. In the following statement, we denote  .
.
Lemma 2.4.
Assume that

for all  . If
. If  , then
, then  has a fixed point.
has a fixed point.
Proof.
It is easy to see that  is a contraction map. In fact, since
is a contraction map. In fact, since  and
and  are bounded linear maps, we have
are bounded linear maps, we have

which implies that  is a contraction.
is a contraction.
In what follows we always assume that  satisfies the Lipschitz condition (2.10).
satisfies the Lipschitz condition (2.10).
Under certain conditions we can modify our hypothesis  .
.
Lemma 2.5.
Assume that  and the space
and the space  is dense in
is dense in  . Then
. Then  .
.
Proof.
Let  . There exist sequences
. There exist sequences  in
in  and
and  in
in  such that
such that  as
as  . Let
. Let  be the orthogonal projection on
be the orthogonal projection on  . Therefore,
. Therefore,  as
as  . Since
. Since  and
and  , we can assert that the sequence
, we can assert that the sequence  converges to some element
converges to some element  and the sequence
and the sequence  converges to some element
converges to some element  . Consequently,
. Consequently,  , which completes the proof.
, which completes the proof.
Related to this result, it is worthwhile to point out that if  has a continuous left inverse for each
has a continuous left inverse for each  , then the space
, then the space  is closed. Moreover, if
is closed. Moreover, if  and the range of
and the range of  is a closed subspace, which occurs, for instance, when
is a closed subspace, which occurs, for instance, when  is a finite dimensional space, then
is a finite dimensional space, then  has a continuous left inverse.
has a continuous left inverse.
Theorem 2.6.
Assume that  and condition (2.7) holds. Then
and condition (2.7) holds. Then  for all
for all  .
.
Proof.
Let  be a control vector, and let
be a control vector, and let  be the solution of (1.2) with initial condition
be the solution of (1.2) with initial condition  . In what follows, we apply our construction preceding Lemma 2.4 with the vector
. In what follows, we apply our construction preceding Lemma 2.4 with the vector  . Let
. Let  be a fixed point of
be a fixed point of  . Clearly
. Clearly  and
and  . We set
. We set  . We now apply Lemma 1.1 to
. We now apply Lemma 1.1 to  , with respect to spaces
, with respect to spaces  and
and  . We set
. We set  , and we define
, and we define  , for
, for  . It follows from this construction that
. It follows from this construction that  , and combining the properties of
, and combining the properties of  and
and  , we obtain that
, we obtain that

for  . We can also see directly that (2.12) hods for
. We can also see directly that (2.12) hods for  . We select a sequence
. We select a sequence  such that
such that  as
as  goes to infinity and
goes to infinity and  . We denote by
. We denote by  the solution of (2.12) when we substitute
the solution of (2.12) when we substitute  by
by  . Hence, we can write
. Hence, we can write

This expression and (2.3) show that  is the solution of the equation
is the solution of the equation

with initial condition  . Therefore,
. Therefore,  . Since the solution of (2.3) depends continuously on
. Since the solution of (2.3) depends continuously on  , we infer that
, we infer that  converges to
converges to  as
as  . Consequently,
. Consequently,  . Hence, from our previous considerations, we can assert that
. Hence, from our previous considerations, we can assert that

which completes the proof.
Now we are able to establish the following criteria for the approximate controllability of system (1.1). The next property is an immediate consequence of Theorem 2.6.
Theorem 2.7.
Assume that  , the control system (1.2) is approximately controllable on
, the control system (1.2) is approximately controllable on  and the space
and the space  . Then the system (1.1) is approximately controllable on
. Then the system (1.1) is approximately controllable on  .
.
We are also in a position to establish the following result.
Theorem 2.8.
Assume that the following conditions hold:
-
(a)
the control system (1.2) is approximately controllable in finite time;
-
(b)
for all
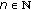 , the space
, the space  ;
; -
(c)
for all
 ,
,  .
.
Then system (1.1) is approximately controllable in finite time.
Proof.
Proceeding as in the proof of Theorem 2.6, we can write

which shows that  is dense in
is dense in  .
.
Similar results for approximate controllability to the origin can be established. On the other hand, with appropriate hypotheses we can estimate the controls involved in the strategies of controllability and approximate controllability. This property allows us to compare the controllability in spaces of infinite dimension with the controllability in spaces of finite dimension.
Theorem 2.9.
Assume that the control system (1.2) is controllable on  , condition (2.7) holds, each operator
, condition (2.7) holds, each operator  has a continuous left inverse
has a continuous left inverse  , for
, for  , and
, and  . Then there exists constants
. Then there exists constants  such that for every
such that for every  and
and  there exists a control sequence
there exists a control sequence  ,
,  , with
, with  and
and  , where
, where  ,
,  , is the solution of (1.1) corresponding to
, is the solution of (1.1) corresponding to  .
.
Proof.
It follows from the controllability of system (1.2) that  is a surjective bounded linear map. We infer that there exists a constant
is a surjective bounded linear map. We infer that there exists a constant  such that for each
such that for each  there exists
there exists  such that
such that  and
and  . Let
. Let  ,
,  , be the solution of (1.2) corresponding to
, be the solution of (1.2) corresponding to  . Since
. Since  and
and  are uniformly bounded for
are uniformly bounded for  , we can conclude that there exists a constant
, we can conclude that there exists a constant  such that
such that  for
for  . In the rest of this proof we apply the construction carried out in the proof of Theorem 2.6. Let
. In the rest of this proof we apply the construction carried out in the proof of Theorem 2.6. Let  be the fixed point of
be the fixed point of  . From
. From

we deduce that

which in turn implies that

which we abbreviate as

Proceeding in a similar way, we can obtain an estimate

Hence,  can also be estimated as
can also be estimated as

We can choose a sequence  such that
such that  and
and  as
as  . Therefore, we can take
. Therefore, we can take  large enough such that
large enough such that  . Since
. Since  is the solution of (1.1) corresponding to controls
is the solution of (1.1) corresponding to controls  , to complete the proof we only need to estimate
, to complete the proof we only need to estimate

and the assertion is consequence of (2.22).
2.1. The Finite-Dimensional Case
Certainly condition (2.7) considered in our previous results is strong. However, the following property holds.
Theorem 2.10.
Assume that  is a space of finite dimension. Then the linear system (1.2) is controllable on
is a space of finite dimension. Then the linear system (1.2) is controllable on  if, and only if, condition (2.7) holds.
if, and only if, condition (2.7) holds.
Proof.
Since  has finite dimension,
has finite dimension,  . Assume initially that system (1.2) is controllable on
. Assume initially that system (1.2) is controllable on  . Let
. Let  . Using the property of controllability, it follows from [4, Corollary
. Using the property of controllability, it follows from [4, Corollary  .3.1] that there exists
.3.1] that there exists  such that
such that

We define  for
for  . This implies that
. This implies that

which shows that  .
.
Conversely, assume that condition (2.7) holds; for  we define
we define  . Applying (2.7), we derive the existence of
. Applying (2.7), we derive the existence of  and
and  such that
such that  . The solution of (1.2) is given by
. The solution of (1.2) is given by

which completes the proof.
We will apply Theorem 2.10 to reduce the study of controllability of system (1.1) to the controllability of systems with finite-dimensional state space.
Corollary 2.11.
Assume that  is a space of finite dimension and that the linear system (1.2) is controllable on
is a space of finite dimension and that the linear system (1.2) is controllable on  . Then there exists
. Then there exists  such that nonlinear system (1.1) is approximately controllable on
such that nonlinear system (1.1) is approximately controllable on  when
when  .
.
Proof.
The assertion is an immediate consequence of Theorems 2.10 and 2.7.
Next we specialize our developments to consider systems where the associated linear system is invariant. Specifically, we will assume that  and
and  for
for  . That is to say, we will be concerned with the nonlinear system
. That is to say, we will be concerned with the nonlinear system

with linear part

In this situation, the subspaces  are nondecreasing. Hence, we get the following immediate consequence.
are nondecreasing. Hence, we get the following immediate consequence.
Proposition 2.12.
Assume that  is a space of finite dimension. If the system (2.28) is approximately controllable in finite time, then it is controllable on
is a space of finite dimension. If the system (2.28) is approximately controllable in finite time, then it is controllable on  , for some
, for some  .
.
Proof.
Since  and
and  are closed subspaces, then there is
are closed subspaces, then there is  such that
such that  .
.
2.2. The Projections 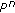
Next we will study a property of projections  . We begin with some remarks.
. We begin with some remarks.
Remark 2.13.
Let  . Since
. Since

we infer that  if, and only if,
if, and only if,

Hence, if  and we define
and we define  and
and  , then
, then  .
.
Lemma 2.14.
Assume that condition (2.7) holds for  and
and  . Then
. Then

where  .
.
Proof.
We decompose  , where
, where  .
.
Let  and
and  . Then
. Then  , where
, where  . We set
. We set  and
and  . It follows from Remark 2.13 that
. It follows from Remark 2.13 that  , and
, and  and
and  . Therefore, using the properties of projections
. Therefore, using the properties of projections  and
and  established in Lemma 1.1, we get
established in Lemma 1.1, we get

Similarly, since  , we can decompose
, we can decompose  , where
, where  . We set
. We set  and
and  . It follows from Remark 2.13 that
. It follows from Remark 2.13 that  , and
, and  and
and  . Consequently, we have
. Consequently, we have

Collecting these assertions, we get

We say that a sequence  is an approximation scheme for
is an approximation scheme for  associated to system (2.27) if
associated to system (2.27) if  are finite-dimensional subspaces of
are finite-dimensional subspaces of  ,
,  are bounded linear projections with
are bounded linear projections with  and
and  , and the following conditions are fulfilled:
, and the following conditions are fulfilled:
-
(i)
the subspaces
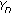 and
and  are invariant under
are invariant under  ;
; -
(ii)
the projections
 are uniformly bounded with
are uniformly bounded with 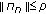 for all
for all 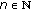 ;
; -
(iii)
for all
 ,
,  as
as 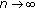 .
.
We consider the control systems


in the space  . We set
. We set  .
.
Theorem 2.15.
If the system (2.28) is approximately controllable in finite time, then the system (2.36) is controllable on an interval  for each
for each  .
.
Proof.
We consider a fixed  . It is immediate from our definition of approximation scheme that if
. It is immediate from our definition of approximation scheme that if  and we consider the same values of
and we consider the same values of  in (2.28) and (2.36), then
in (2.28) and (2.36), then  for all
for all  . Let
. Let  . It follows from the previous remark, that if we select
. It follows from the previous remark, that if we select  such that
such that  as
as  , then
, then

which shows that  as
as  . Hence, system (2.36) is approximately controllable in finite time. The assertion is now a consequence of Proposition 2.12.
. Hence, system (2.36) is approximately controllable in finite time. The assertion is now a consequence of Proposition 2.12.
To simplify the writing of the text, next we will assume that  and
and  . Furthermore, we take an orthonormal basis
. Furthermore, we take an orthonormal basis  of
of  , and
, and  is the orthogonal projection. We can establish the following property.
is the orthogonal projection. We can establish the following property.
Lemma 2.16.
Assume that condition (2.7) holds in  for all
for all  . Then there are constants
. Then there are constants  such that
such that

for all  ,
,  .
.
Proof.
We proceed by using mathematical induction. The assertion holds for  . In fact, since
. In fact, since  and
and  , then
, then  and
and

Assume now that the assertion is fulfilled for  . We will prove that the assertion holds for
. We will prove that the assertion holds for  . For
. For  ,
,  , we decompose
, we decompose  , where
, where  . We abbreviate the notation by writing
. We abbreviate the notation by writing  . Consequently, applying Lemma 2.14, we get
. Consequently, applying Lemma 2.14, we get

On the other hand, since  is a bounded linear map on
is a bounded linear map on  , then there exists a constant
, then there exists a constant  such that
such that

and substituting these estimates in (2.40), we get that the assertion is fulfilled for  .
.
Lemma 2.17.
Assume that  , condition (2.7) holds in
, condition (2.7) holds in  for all
for all  , and that the function
, and that the function  in (2.35) satisfies the Lipschitz conditions
in (2.35) satisfies the Lipschitz conditions

where  . If
. If

then the map  defined in
defined in  is a contraction.
is a contraction.
Proof.
It follows from our definition that

On the other hand, since

applying Lemma 2.16 and the definition of  , we have
, we have

In view of

collecting the above estimate, we get the assertion.
Using now Theorem 2.15 and Lemma 2.17 we can emphasize the assertion of Corollary 2.11.
Corollary 2.18.
Under the conditions of Lemma 2.17, if the system (2.28) is approximately controllable in finite time, then the system (2.35) is approximately controllable on  for each
for each  .
.
Remark 2.19.
Under the above conditions, we can apply Theorem 2.9 in the space  . Consequently, there exist constants
. Consequently, there exist constants  and
and  such that for every
such that for every  and
and  , there exists a sequence of controls
, there exists a sequence of controls  for
for  such that
such that  ,
,  , and
, and  , where
, where  is the solution of (2.35) corresponding to controls
is the solution of (2.35) corresponding to controls  . Furthermore, we denote
. Furthermore, we denote  , where
, where  are the constants involved in (2.10), and we assume that
are the constants involved in (2.10), and we assume that

Finally, we are in a position to establish the following result of controllability.
Theorem 2.20.
Assume that there exists an approximation scheme  and the system (2.28) is approximately controllable in finite time. If, in addition,
and the system (2.28) is approximately controllable in finite time. If, in addition,  ,
,  , and
, and  and
and  as
as  , then the system (2.27) is also approximately controllable in finite time.
, then the system (2.27) is also approximately controllable in finite time.
Proof.
Let  and
and  . It follows from Corollary 2.18 that system (2.35) is approximately controllable on
. It follows from Corollary 2.18 that system (2.35) is approximately controllable on  . Since
. Since  as
as  , for
, for  , we chose
, we chose  such that
such that  . It follows from Remark 2.19 that there exists a sequence of controls
. It follows from Remark 2.19 that there exists a sequence of controls  for
for  such that
such that  ,
,  and
and  , where
, where  is the solution of (2.35) corresponding to controls
is the solution of (2.35) corresponding to controls  .
.
We denote  for the solution of system
for the solution of system

and we set  . It follows from (2.35) and (2.49) that
. It follows from (2.35) and (2.49) that

which implies that

Consequently,  . Hence,
. Hence,

Consequently,  as
as  , which completes the proof.
, which completes the proof.
3. Application
We complete this paper with an application of the results established in Section 2.
In this application we are concerned with a general class of systems that satisfy the conditions considered previously. Specifically, we consider a control system of type (1.1) with state space  of infinite dimension and operators
of infinite dimension and operators  and
and  for
for  .
.
We assume that  is a bounded self-adjoint operator with distinct eigenvalues
is a bounded self-adjoint operator with distinct eigenvalues  ,
,  , and
, and  is an orthonormal basis of
is an orthonormal basis of  consisting of eigenvectors of
consisting of eigenvectors of  corresponding to eigenvalues
corresponding to eigenvalues  , respectively.
, respectively.
We take as control space  , and
, and  is given by
is given by  , where
, where  is a vector such that
is a vector such that  , for all
, for all  . It is clear that condition (2.7) does not hold in this case. In fact, since the space
. It is clear that condition (2.7) does not hold in this case. In fact, since the space  is closed, if we assume that condition (2.7) is fulfilled, then for every
is closed, if we assume that condition (2.7) is fulfilled, then for every  there is
there is  such that
such that  . In particular, for an arbitrary
. In particular, for an arbitrary  and
and  and applying Remark 2.13, we obtain that
and applying Remark 2.13, we obtain that  . However, this means that
. However, this means that  is a finite-dimensional space, which is a contradiction. Let
is a finite-dimensional space, which is a contradiction. Let  be given by
be given by

where  are functions such that
are functions such that  and the following Lipschitz conditions
and the following Lipschitz conditions

are verified for all  ,
,  , and
, and  . We assume that
. We assume that

We denote  .
.
Let  , and let
, and let  be the orthogonal projection on
be the orthogonal projection on  . We set
. We set  . Since
. Since  is invariant under
is invariant under  , we can consider the system
, we can consider the system

with  , which is the restriction of system (1.2) on
, which is the restriction of system (1.2) on  . It is well known that system (3.4) is exactly controllable on
. It is well known that system (3.4) is exactly controllable on  , for every
, for every  . Furthermore,
. Furthermore,

Let  ,
,  , be the constants introduced in Lemma 2.16, and let
, be the constants introduced in Lemma 2.16, and let  be the constants introduced in Remark 2.19. At this point it is worth to note that the constants
be the constants introduced in Remark 2.19. At this point it is worth to note that the constants  for
for  and
and  depend on
depend on  and
and  for
for  and
and  while
while  and
and  depend on
depend on  and
and  , respectively, for
, respectively, for  . We can establish the following immediate consequence of Theorem 2.20.
. We can establish the following immediate consequence of Theorem 2.20.
Proposition 3.1.
Assume that the system (2.28) is approximately controllable in finite time. If, in addition,  ,
,  ,
,

and  and
and  , as
, as  , then the system (2.27) is also approximately controllable in finite time.
, then the system (2.27) is also approximately controllable in finite time.
References
Bittanti S, Bolzern P: Reachability and controllability of discrete-time linear periodic systems. IEEE Transactions on Automatic Control 1985,30(4):399-401. 10.1109/TAC.1985.1103961
Guermah S, Djennoune S, Bettayeb M: Controllability and observability of linear discrete-time fractional-order systems. International Journal of Applied Mathematics and Computer Science 2008,18(2):213-222. 10.2478/v10006-008-0019-6
Ichikawa A: Null controllability with vanishing energy for discrete-time systems. Systems & Control Letters 2008,57(1):34-38. 10.1016/j.sysconle.2007.06.008
Klamka J: Controllability of Dynamical Systems, Mathematics and Its Applications (East European Series). Volume 48. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1991:xvi+248.
Leiva H, Uzcategui J: Exact controllability for semilinear difference equation and application. Journal of Difference Equations and Applications 2008,14(7):671-679. 10.1080/10236190701726170
Negreanu M, Zuazua E: Uniform boundary controllability of a discrete 1-D wave equation. Systems & Control Letters 2003,48(3-4):261-279. 10.1016/S0167-6911(02)00271-2
Phat VN: Controllability of nonlinear discrete systems without differentiability assumption. Optimization 1988,19(1):133-142. 10.1080/02331938808843327
Son NK: Approximate controllability with positive controls. Acta Mathematica Vietnamica 1997,22(2):589-620.
Weiss G: Memoryless output feedback nullification and canonical forms, for time varying systems. International Journal of Control 2005,78(15):1174-1181. 10.1080/0020710500291986
Zhang X, Zheng C, Zuazua E: Time discrete wave equations: boundary observability and control. Discrete and Continuous Dynamical Systems. Series A 2009,23(1-2):571-604.
Zheng C: Controllability of the time discrete heat equation. Asymptotic Analysis 2008,59(3-4):139-177.
Bensoussan A, Da Prato G, Delfour MC, Mitter SK: Representation and Control of Infinite-Dimensional Systems. Vol. 1, Systems & Control: Foundations & Applications. Birkhäuser, Boston, Mass, USA; 1992:xiv+315.
Bensoussan A, Da Prato G, Delfour MC, Mitter SK: Representation and Control of Infinite-Dimensional Systems. Vol. II, Systems & Control: Foundations & Applications. Birkhäuser, Boston, Mass, USA; 1993:xviii+345.
Curtain RF, Zwart H: An Introduction to Infinite-Dimensional Linear Systems Theory, Texts in Applied Mathematics. Volume 21. Springer, New York, NY, USA; 1995:xviii+698.
Louis J-C, Wexler D: On exact controllability in Hilbert spaces. Journal of Differential Equations 1983,49(2):258-269. 10.1016/0022-0396(83)90014-1
Henríquez HR: On non-exact controllable systems. International Journal of Control 1985,42(1):71-83. 10.1080/00207178508933347
Gaĭshun IV: Controllability and stabilizability of discrete systems in a function space on a commutative semigroup. Differential Equations 2004,40(6):873-882. 10.1023/B:DIEQ.0000046864.27700.e9
Klamka J: Controllability of nonlinear discrete systems. International Journal of Applied Mathematics and Computer Science 2002,12(2):173-180.
Komornik V: Exact Controllability and Stabilization, The Multiplier Method, RAM: Research in Applied Mathematics. Masson, Paris, France; 1994:viii+156.
Sasu B, Sasu AL: Stability and stabilizability for linear systems of difference equations. Journal of Difference Equations and Applications 2004,10(12):1085-1105. 10.1080/10236190412331314178
Sasu AL: Stabilizability and controllability for systems of difference equations. Journal of Difference Equations and Applications 2006,12(8):821-826. 10.1080/10236190600734218
Zabczyk J: Mathematical Control Theory: An Introduction. Birkhäuser, Boston, Mass, USA; 1995.
Sukavanam N: Approximate controllability of semilinear control systems with growing nonlinearity. In Mathematical Theory of Control (Bombay, 1990), Lecture Notes in Pure and Appl. Math.. Volume 142. Dekker, New York, NY, USA; 1993:353-357.
Acknowledgments
The authors are grateful to the referees for providing nice comments and suggestions. H. R. Henríquez was supported in part by CONICYT under Grant FONDECYT no. 1090009. C. Cuevas was partially supported by CNPq/Brazil.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Henríquez, H.R., Cuevas, C. Approximate Controllability of Abstract Discrete-Time Systems. Adv Differ Equ 2010, 695290 (2010). https://doi.org/10.1155/2010/695290
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/695290
 if
if  is dense in
is dense in 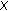 ,
, is dense in
is dense in 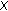 ,
, if
if 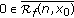 for every
for every 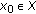 ,
, for every
for every 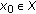 .
.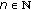 , the space
, the space  ;
; ,
,  .
.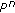
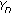 and
and  are invariant under
are invariant under  ;
; are uniformly bounded with
are uniformly bounded with 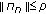 for all
for all 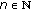 ;
; ,
,  as
as 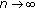 .
.