Exponential Stability and Global Attractors for a Thermoelastic Bresse System

Abstract

We consider the stability properties for thermoelastic Bresse system which describes the motion of a linear planar shearable thermoelastic beam. The system consists of three wave equations and two heat equations coupled in certain pattern. The two wave equations about the longitudinal displacement and shear angle displacement are effectively damped by the dissipation from the two heat equations. We use multiplier techniques to prove the exponential stability result when the wave speed of the vertical displacement coincides with the wave speed of the longitudinal or of the shear angle displacement. Moreover, the existence of the global attractor is firstly achieved.

1. Introduction

In this paper, we will consider the following system:

(1.1)

(1.2)

(1.3)

(1.4)

(1.5)

together with initial conditions

(1.6)

and boundary conditions

(1.7)

where , , and are the longitudinal, vertical, and shear angle displacement, and are the temperature deviations from the along the longitudinal and vertical directions, , , , , , , , and are positive constants for the elastic and thermal material properties.

From this seemingly complicated system, very interesting special cases can be obtained. In particular, the isothermal system is exactly the system obtained by Bresse [1] in 1856. The Bresse system, (1.1)–(1.3) with , removed, is more general than the well-known Timoshenko system where the longitudinal displacement is not considered. If both and are neglected, the Bresse thermoelastic system simplifies to the following Timoshenko thermoelastic system:

(1.8)

which was studied by Messaoudi and Said-Houari [2]. For the boundary conditions

(1.9)

they obtained exponential stability for the thermoelastic Timoshenko system (1.8) when ; later, they proved energy decay for a Timoshenko-type system with history in thermoelasticity of type III [3], and this paper is similar to [2] with an extra damping that comes from the presence of a history term; it improves the result of [2] in the sense that the case of nonequal wave speed has been considered and the relaxation function g is allowed to decay exponentially or polynomially. We refer the reader to [4–10] for the Timoshenko system with other kinds of damping mechanisms such as viscous damping, viscoelastic damping of Boltzmann type acting on the motion equation of or . In all these cases, the rotational displacement of the Timoshenko system is effectively damped due to the thermal energy dissipation. In fact, the energy associated with this component of motion decays exponentially. The transverse displacement is only indirectly damped through the coupling, which can be observed from (1.2). The effectiveness of this damping depends on the type of coupling and the wave speeds. When the wave speeds are the same (), the indirect damping is actually strong enough to induce exponential stability for the Timoshenko system, but when the wave speeds are different, the Timoshenko system loses the exponential stability. This phenomenon has been observed for partially damped second-order evolution equations. We would like to mention other works in [11–15] for other related models.

Recently, Liu and Rao [16] considered a similar system; they used semigroup method and showed that the exponentially decay rate is preserved when the wave speed of the vertical displacement coincides with the wave speed of longitudinal displacement or of the shear angle displacement. Otherwise, only a polynomial-type decay rate can be obtained; their main tools are the frequency-domain characterization of exponential decay obtained by Prüss [17] and Huang [18] and of polynomial decay obtained recently by Muñoz Rivera and Fernández Sare [5]. For the attractors, we refer to [19–24].

In this paper, we consider system (1.1)–(1.5); that is, we use multiplier techniques to prove the exponential stability result only for . However, from the theory of elasticity, and denote Young's modulus and the shear modulus, respectively. These two elastic moduli are not equal since

(1.10)

where is the Poisson's ratio. Thus, the exponential stability for the case of is only mathematically sound. However, it does provide useful insight into the study of similar models arising from other applications.

2. Equal Wave Speeds Case: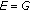  

Here we state and prove a decay result in the case of equal wave speeds propagation.

Define the state spaces

(2.1)

where

(2.2)

The associated energy term is given by

(2.3)

By a straightforward calculation, we have

(2.4)

From semigroup theory [25, 26], we have the following existence and regularity result; for the explicit proofs, we refer the reader to [16].

Lemma 2.1.

Let be given. Then problem (1.1)–(1.5) has a unique global weak solution verifying

(2.5)

We are now ready to state our main stability result.

Theorem 2.2.

Suppose that and . Then the energy decays exponentially as time tends to infinity; that is, there exist two positive constants and μ independent of the initial data and , such that

(2.6)

The proof of our result will be established through several lemmas.

Let

(2.7)

where is the solution of

(2.8)

Lemma 2.3.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.9)

Proof.

(2.10)

By using the inequalities

(2.11)

and Young's inequality, the assertion of the lemma follows.

Let

(2.12)

Lemma 2.4.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.13)

Proof.

Using (1.4) and (1.1), we get

(2.14)

The assertion of the lemma then follows, using Young's and Poincaré's inequalities.

Let

(2.15)

Lemma 2.5.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.16)

Proof.

Using (1.3) and (1.5), we have

(2.17)

Then, using Young's and Poincaré's inequalities, we can obtain the assertion.

Next, we set

(2.18)

Lemma 2.6.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.19)

Proof.

Letting , , then using (1.2), (1.3), we have

(2.20)

Noticing that , then

(2.21)

Then, using Young's inequality, we can obtain the assertion.

We set

(2.22)

Lemma 2.7.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.23)

Proof.

Let , , then using (1.1), (1.2), we have

(2.24)

Then, noticing , again, from the above two equalities and Young's inequality, we can obtain the assertion.

Next, we set

(2.25)

Lemma 2.8.

Letting , , , , be a solution of (1.1)–(1.5), then one has

(2.26)

Proof.

Using (1.1), (1.2), we have

(2.27)

Noticing (2.3) and (2.4), we have that satisfy the following:

(2.28)

Similarly,

(2.29)

Then, insert (2.28) and (2.29) into (2.27), and the assertion of the lemma follows.

Now, we set

(2.30)

Lemma 2.9.

Letting , , , , be a solution of (1.1)–(1.5), then one has, for all ,

(2.31)

Proof.

Using (1.5), we have

(2.32)

Then, using Young's and Poincaré's inequalities, we can obtain the assertion.

Now, letting , we define the Lyapunov functional as follows:

(2.33)

By using (2.4), (2.9), (2.13), (2.16), (2.19), (2.23), (2.26), and (2.31), we have

(2.34)

where

(2.35)

We can choose big enough, small enough, and

(2.36)

Then are all negative constants; at this point, there exists a constant , and (2.34) takes the form

(2.37)

We are now ready to prove Theorem 2.2.

Proof of Theorem 2.2.

Firstly, from the definition of , we have

(2.38)

which, from (2.37) and (2.38), leads to

(2.39)

Integrating (2.39) over and using (2.38) lead to (2.6). This completes the proof of Theorem 2.2.

3. Global Attractors

In this section, we establish the existence of the global attractor for system (1.1)–(1.5).

Setting , , , , then, (1.1)–(1.5) can be transformed into the system

(3.1)

We consider the problem in the following Hilbert space:

(3.2)

Recall that the global attractor of acting on is a compact set enjoying the following properties:

(1) is fully invariant for , that is, for every ;

(2) is an attracting set, namely, for any bounded set ,

(3.3)

where denotes the Hausdorff semidistance on .

More details on the subject can be found in the books [23, 26, 27].

Remark 3.1.

The uniform energy estimate (2.6) implies the existence of a bounded absorbing set for the semigroup . Indeed, if is any ball of , then for any bounded set , it is immediate to see that there exists such that

(3.4)

for every .

Moreover, if we define

(3.5)

it is clear that is still a bounded absorbing set which is also invariant for , that is, for every .

In the sequel, we define the operator as with Dirichlet boundary conditions. It is well known that is a positive operator on with domain . Moreover, we can define the powers of for . The space turns out to be a Hilbert space with the inner product

(3.6)

where stands for -inner product on .

In particular, , , and . The injection is compact whenever . For further convenience, for , introduce the Hilbert space

(3.7)

Clearly, .

Now, let , where is the invariant, bounded absorbing set of given by Remark 3.1, and take the inner product in of (3.1) and to get

(3.8)

Here, the boundary term of integration by parts is neglected since we are working with more regular functions. We denote

(3.9)

Then, introduce the functional

(3.10)

By repeating similar argument as in the proofs of Lemmas 2.3–2.9 and (3.8), choosing our constants very carefully and properly, we get

(3.11)

On the other hand,

(3.12)

so that

(3.13)

which gives

(3.14)

Let be the ball of ; from the compact embedding , is compact in . Then, due to the compactness of , for every fixed and every , there exist finitely many balls of of radius such that belongs to the union of such balls, for every . This implies that

(3.15)

where is the Kuratowski measure of noncompactness, defined by

(3.16)

Since the invariant, connected, bounded absorbing set fulfills (3.15), exploiting a classical result of the theory of attractors of semigroups (see, e.g., [28]), we conclude that the -limit set of , that is,

(3.17)

is a connected and compact global attractor of . Therefore, we have proved the following result.

Theorem 3.2.

Under the assumption of , problem (3.1) possesses a unique global attractor .