- Research Article
- Open access
- Published:
Solvability of a Higher-Order Nonlinear Neutral Delay Difference Equation
Advances in Difference Equations volume 2010, Article number: 767620 (2010)
Abstract
The existence of bounded nonoscillatory solutions of a higher-order nonlinear neutral delay difference equation  ,
,  , where
, where  ,
,  ,
,  , and
, and  are integers,
are integers,  and
and  are real sequences,
are real sequences,  , and
, and  is a mapping, is studied. Some sufficient conditions for the existence of bounded nonoscillatory solutions of this equation are established by using Schauder fixed point theorem and Krasnoselskii fixed point theorem and expatiated through seven theorems according to the range of value of the sequence
is a mapping, is studied. Some sufficient conditions for the existence of bounded nonoscillatory solutions of this equation are established by using Schauder fixed point theorem and Krasnoselskii fixed point theorem and expatiated through seven theorems according to the range of value of the sequence  . Moreover, these sufficient conditions guarantee that this equation has not only one bounded nonoscillatory solution but also uncountably many bounded nonoscillatory solutions.
. Moreover, these sufficient conditions guarantee that this equation has not only one bounded nonoscillatory solution but also uncountably many bounded nonoscillatory solutions.
1. Introduction and Preliminaries
Recently, the interest in the study of the solvability of difference equations has been increasing (see [1–17] and references cited therein). Some authors have paied their attention to various difference equations. For example,

(see [14]),

(see [11]),

(see [6]),

(see [10]),

(see [9]),

(see [8]),

(see [15]),


(see [16]),

(see [17]).
Motivated and inspired by the papers mentioned above, in this paper, we investigate the following higher-order nonlinear neutral delay difference equation:

where  ,
,  ,
,  , and
, and  are integers,
are integers,  and
and  are real sequences,
are real sequences,  , and
, and  is a mapping. Clearly, difference equations (1.1)–(1.10) are special cases of (1.11). By using Schauder fixed point theorem and Krasnoselskii fixed point theorem, the existence of bounded nonoscillatory solutions of (1.11) is established.
is a mapping. Clearly, difference equations (1.1)–(1.10) are special cases of (1.11). By using Schauder fixed point theorem and Krasnoselskii fixed point theorem, the existence of bounded nonoscillatory solutions of (1.11) is established.
Lemma 1.1 (Schauder fixed point theorem).
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  . Let
. Let  be a continuous mapping such that
be a continuous mapping such that  is a relatively compact subset of
is a relatively compact subset of  . Then
. Then  has at least one fixed point in
has at least one fixed point in  .
.
Lemma 1.2 (Krasnoselskii fixed point theorem).
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  , and let
, and let  satisfy
satisfy  for each
for each  . If
. If  is a contraction mapping and
is a contraction mapping and  is a completely continuous mapping, then the equation
is a completely continuous mapping, then the equation  has at least one solution in
has at least one solution in  .
.
The forward difference  is defined as usual, that is,
is defined as usual, that is,  . The higher-order difference for a positive integer
. The higher-order difference for a positive integer  is defined as
is defined as  ,
,  . Throughout this paper, assume that
. Throughout this paper, assume that  ,
,  and
and  stand for the sets of all positive integers and integers, respectively,
stand for the sets of all positive integers and integers, respectively,  ,
,  ,
,  ,
,  , and
, and  denotes the set of real sequences defined on the set of positive integers lager than
denotes the set of real sequences defined on the set of positive integers lager than  where any individual sequence is bounded with respect to the usual supremum norm
where any individual sequence is bounded with respect to the usual supremum norm  for
for  . It is well known that
. It is well known that  is a Banach space under the supremum norm. A subset
is a Banach space under the supremum norm. A subset  of a Banach space
of a Banach space  is relatively compact if every sequence in
is relatively compact if every sequence in  has a subsequence converging to an element of
has a subsequence converging to an element of  .
.
Definition 1.3 (see [5]).
A set  of sequences in
of sequences in  is uniformly Cauchy (or equi-Cauchy) if, for every
is uniformly Cauchy (or equi-Cauchy) if, for every  , there exists an integer
, there exists an integer  such that
such that

whenever  for any
for any  in
in  .
.
Lemma 1.4 (discrete Arzela-Ascoli's theorem [5]).
A bounded, uniformly Cauchy subset  of
of  is relatively compact.
is relatively compact.
Let

Obviously,  is a bounded closed and convex subset of
is a bounded closed and convex subset of  . Put
. Put

By a solution of (1.11), we mean a sequence  with a positive integer
with a positive integer  such that (1.11) is satisfied for all
such that (1.11) is satisfied for all  . As is customary, a solution of (1.11) is said to be oscillatory about zero, or simply oscillatory, if the terms
. As is customary, a solution of (1.11) is said to be oscillatory about zero, or simply oscillatory, if the terms  of the sequence
of the sequence  are neither eventually all positive nor eventually all negative. Otherwise, the solution is called nonoscillatory.
are neither eventually all positive nor eventually all negative. Otherwise, the solution is called nonoscillatory.
2. Existence of Nonoscillatory Solutions
In this section, a few sufficient conditions of the existence of bounded nonoscillatory solutions of (1.11) are given.
Theorem 2.1.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  , and
, and  such that, for
such that, for  ,
,




Then (1.11) has a bounded nonoscillatory solution in  .
.
Proof.
Choose  . By (2.1), (2.4), and the definition of convergence of series, an integer
. By (2.1), (2.4), and the definition of convergence of series, an integer  can be chosen such that
can be chosen such that


Define a mapping  by
by

for all  .
.
-
(i)
It is claimed that
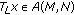 , for all
, for all 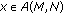 .
.
In fact, for every  and
and  , it follows from (2.3) and (2.6) that
, it follows from (2.3) and (2.6) that

That is,  .
.
-
(ii)
It is declared that
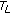 is continuous.
is continuous.
Let  and
and  be any sequence such that
be any sequence such that  as
as  . For
. For  , (2.2) guarantees that
, (2.2) guarantees that

This inequality and (2.4) imply that  is continuous.
is continuous.
-
(iii)
It can be asserted that
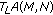 is relatively compact.
is relatively compact.
By (2.4), for any  , take
, take  large enough so that
large enough so that

Then, for any  and
and  , (2.10) ensures that
, (2.10) ensures that

which means that  is uniformly Cauchy. Therefore, by Lemma 1.4,
is uniformly Cauchy. Therefore, by Lemma 1.4,  is relatively compact.
is relatively compact.
By Lemma 1.1, there exists  such that
such that  , which is a bounded nonoscillatory solution of (1.11). In fact, for
, which is a bounded nonoscillatory solution of (1.11). In fact, for  ,
,

which derives that

That is,

by which it follows that

Therefore,  is a bounded nonoscillatory solution of (1.11). This completes the proof.
is a bounded nonoscillatory solution of (1.11). This completes the proof.
Remark 2.2.
The conditions of Theorem 2.1 ensure the (1.11) has not only one bounded nonoscillatory solution but also uncountably many bounded nonoscillatory solutions. In fact, let  with
with  . For
. For  and
and  , as the preceding proof in Theorem 2.1, there exist integers
, as the preceding proof in Theorem 2.1, there exist integers  and mappings
and mappings  satisfying (2.5)–(2.7), where
satisfying (2.5)–(2.7), where  are replaced by
are replaced by  ,
,  and
and  ,
,  , respectively, and
, respectively, and 
 for some
for some  . Then the mappings
. Then the mappings  and
and  have fixed points
have fixed points  , respectively, which are bounded nonoscillatory solutions of (1.11) in
, respectively, which are bounded nonoscillatory solutions of (1.11) in  . For the sake of proving that (1.11) possesses uncountably many bounded nonoscillatory solutions in
. For the sake of proving that (1.11) possesses uncountably many bounded nonoscillatory solutions in  , it is only needed to show that
, it is only needed to show that  . In fact, by (2.7), we know that, for
. In fact, by (2.7), we know that, for  ,
,

Then,

that is,  .
.
Theorem 2.3.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Proof.
Choose  . By (2.18) and (2.4), an integer
. By (2.18) and (2.4), an integer  can be chosen such that
can be chosen such that

Define a mapping  by
by

for all  .
.
The proof that  has a fixed point
has a fixed point  is analogous to that in Theorem 2.1. It is claimed that the fixed point
is analogous to that in Theorem 2.1. It is claimed that the fixed point  is a bounded nonoscillatory solution of (1.11). In fact, for
is a bounded nonoscillatory solution of (1.11). In fact, for  ,
,

by which it follows that

The rest of the proof is similar to that in Theorem 2.1. This completes the proof.
Theorem 2.4.
Assume that there exist constants  ,
,  , and
, and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Proof.
Choose  . By (2.23) and (2.4), an integer
. By (2.23) and (2.4), an integer  can be chosen such that
can be chosen such that

Define two mappings  by
by

for all  .
.
-
(i)
It is claimed that
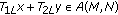 , for all
, for all 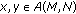 .
.
In fact, for every  and
and  , it follows from (2.3), (2.24) that
, it follows from (2.3), (2.24) that

That is,  .
.
-
(ii)
It is declared that
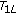 is a contraction mapping on
is a contraction mapping on  .
.
In reality, for any  and
and  , it is easy to derive that
, it is easy to derive that

which implies that

Then,  ensures that
ensures that  is a contraction mapping on
is a contraction mapping on  .
.
-
(iii)
Similar to (ii) and (iii) in the proof of Theorem 2.1, it can be showed that
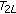 is completely continuous.
is completely continuous.
By Lemma 1.2, there exists  such that
such that  , which is a bounded nonoscillatory solution of (1.11). This completes the proof.
, which is a bounded nonoscillatory solution of (1.11). This completes the proof.
Theorem 2.5.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Proof.
Choose  . By (2.29) and (2.4), an integer
. By (2.29) and (2.4), an integer  can be chosen such that
can be chosen such that

Define two mappings  as (2.25). The rest of the proof is analogous to that in Theorem 2.4. This completes the proof.
as (2.25). The rest of the proof is analogous to that in Theorem 2.4. This completes the proof.
Similar to the proof of Theorem 2.5, we have the following theorem.
Theorem 2.6.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Theorem 2.7.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Proof.
Take  sufficiently small satisfying
sufficiently small satisfying

Choose  . By (2.33), an integer
. By (2.33), an integer  can be chosen such that
can be chosen such that

Define two mappings  by
by

for all  . The rest of the proof is analogous to that in Theorem 2.4. This completes the proof.
. The rest of the proof is analogous to that in Theorem 2.4. This completes the proof.
Similar to the proof of Theorem 2.7, we have
Theorem 2.8.
Assume that there exist constants  and
and  with
with  and sequences
and sequences  ,
,  ,
,  ,
,  , satisfying (2.2)–(2.4) and
, satisfying (2.2)–(2.4) and

Then (1.11) has a bounded nonoscillatory solution in  .
.
Remark 2.9.
Similar to Remark 2.2, we can also prove that the conditions of Theorems 2.3–2.8 ensure that (1.11) has not only one bounded nonoscillatory solution but also uncountably many bounded nonoscillatory solutions.
Remark 2.10.
Theorems 2.1–2.8 extend and improve Theorem  of Cheng [6], Theorems
of Cheng [6], Theorems  of Liu et al. [8], and corresponding theorems in [3, 4, 9–17].
of Liu et al. [8], and corresponding theorems in [3, 4, 9–17].
3. Examples
In this section, two examples are presented to illustrate the advantage of the above results.
Example 3.1.
Consider the following fourth-order nonlinear neutral delay difference equation:

Choose  and
and  . It is easy to verify that the conditions of Theorem 2.1 are satisfied. Therefore Theorem 2.1 ensures that (3.1) has a nonoscillatory solution in
. It is easy to verify that the conditions of Theorem 2.1 are satisfied. Therefore Theorem 2.1 ensures that (3.1) has a nonoscillatory solution in  . However, the results in [3, 4, 6, 8–17] are not applicable for (3.1).
. However, the results in [3, 4, 6, 8–17] are not applicable for (3.1).
Example 3.2.
Consider the following third-order nonlinear neutral delay difference equation:

where

Choose  and
and  . It can be verified that the assumptions of Theorem 2.5 are fulfilled. It follows from Theorem 2.5 that (3.2) has a nonoscillatory solution in
. It can be verified that the assumptions of Theorem 2.5 are fulfilled. It follows from Theorem 2.5 that (3.2) has a nonoscillatory solution in  . However, the results in [3, 4, 6, 8–17] are unapplicable for (3.2).
. However, the results in [3, 4, 6, 8–17] are unapplicable for (3.2).
References
Agarwal RP: Difference Equations and Inequalities: Theory, Methods, and Application, Monographs and Textbooks in Pure and Applied Mathematics. Volume 228. 2nd edition. Marcel Dekker, New York, NY, USA; 2000:xvi+971.
Agarwal RP, Grace SR, O'Regan D: Oscillation Theory for Difference and Functional Differential Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:viii+337.
Agarwal RP, Thandapani E, Wong PJY: Oscillations of higher-order neutral difference equations. Applied Mathematics Letters 1997,10(1):71-78. 10.1016/S0893-9659(96)00114-0
Agarwal RP, Grace SR: Oscillation of higher-order nonlinear difference equations of neutral type. Applied Mathematics Letters 1999,12(8):77-83. 10.1016/S0893-9659(99)00126-3
Cheng SS, Patula WT: An existence theorem for a nonlinear difference equation. Nonlinear Analysis: Theory, Methods & Applications 1993,20(3):193-203. 10.1016/0362-546X(93)90157-N
Cheng J: Existence of a nonoscillatory solution of a second-order linear neutral difference equation. Applied Mathematics Letters 2007,20(8):892-899. 10.1016/j.aml.2006.06.021
Győri I, Ladas G: Oscillation Theory of Delay Differential Equations, Oxford Mathematical Monographs. The Clarendon Press Oxford University Press, New York, NY, USA; 1991:xii+368.
Liu Z, Xu Y, Kang SM: Global solvability for a second order nonlinear neutral delay difference equation. Computers & Mathematics with Applications 2009,57(4):587-595. 10.1016/j.camwa.2008.09.050
Meng Q, Yan J: Bounded oscillation for second-order nonlinear neutral difference equations in critical and non-critical states. Journal of Computational and Applied Mathematics 2008,211(2):156-172. 10.1016/j.cam.2006.11.008
Migda M, Migda J: Asymptotic properties of solutions of second-order neutral difference equations. Nonlinear Analysis: Theory, Methods & Applications 2005,63(5–7):e789-e799. 10.1016/j.na.2005.02.005
Thandapani E, Manuel MMS, Graef JR, Spikes PW: Monotone properties of certain classes of solutions of second-order difference equations. Computers & Mathematics with Applications 1998,36(10–12):291-297. 10.1016/S0898-1221(98)80030-8
Yang FJ, Liu JC: Positive solution of even-order nonlinear neutral difference equations with variable delay. Journal of Systems Science and Mathematical Sciences 2002,22(1):85-89.
Zhang BG, Yang B: Oscillation in higher-order nonlinear difference equations. Chinese Annals of Mathematics 1999,20(1):71-80.
Zhang Z, Li Q: Oscillation theorems for second-order advanced functional difference equations. Computers & Mathematics with Applications 1998,36(6):11-18. 10.1016/S0898-1221(98)00157-6
Zhou Y: Existence of nonoscillatory solutions of higher-order neutral difference equations with general coefficients. Applied Mathematics Letters 2002,15(7):785-791. 10.1016/S0893-9659(02)00043-5
Zhou Y, Huang YQ: Existence for nonoscillatory solutions of higher-order nonlinear neutral difference equations. Journal of Mathematical Analysis and Applications 2003,280(1):63-76. 10.1016/S0022-247X(03)00017-9
Zhou Y, Zhang BG: Existence of nonoscillatory solutions of higher-order neutral delay difference equations with variable coefficients. Computers & Mathematics with Applications 2003,45(6–9):991-1000. 10.1016/S0898-1221(03)00074-9
Acknowledgment
The authors are grateful to the editor and the referee for their kind help, careful reading and editing, valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, M., Guo, Z. Solvability of a Higher-Order Nonlinear Neutral Delay Difference Equation. Adv Differ Equ 2010, 767620 (2010). https://doi.org/10.1155/2010/767620
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/767620
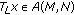 , for all
, for all 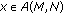 .
.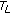 is continuous.
is continuous.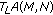 is relatively compact.
is relatively compact.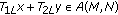 , for all
, for all 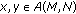 .
.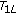 is a contraction mapping on
is a contraction mapping on  .
.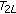 is completely continuous.
is completely continuous.