- Research Article
- Open access
- Published:
Asymptotic Constancy in Linear Difference Equations: Limit Formulae and Sharp Conditions
Advances in Difference Equations volume 2010, Article number: 789302 (2010)
Abstract
It is found that every solution of a system of linear delay difference equations has finite limit at infinity, if some conditions are satisfied. These are much weaker than the known sufficient conditions for asymptotic constancy of the solutions. When we impose some positivity assumptions on the coefficient matrices, our conditions are also necessary. The novelty of our results is illustrated by examples.
1. Introduction
Consider the nonautonomous linear delay difference system

where the following are considered.
(A1) is an integer, and
is an integer, and 

 .
.
(A2) and
and  are sequences of nonnegative integers
are sequences of nonnegative integers  such that
such that

is finite.
Without loss of generality we may (and do) assume the following.
(A3)For each  and
and  ,
,

Under these conditions,  .
.
Whenever the delays are constants, we get the system

where we suppose that
(A4)
 are nonnegative integers and
are nonnegative integers and

In this case,  .
.
Together with the above equations we assume initial conditions of the form

where  . Clearly, (1.1) with (1.6) (and similarly (1.4) with (1.6)) has a unique solution which exists for any
. Clearly, (1.1) with (1.6) (and similarly (1.4) with (1.6)) has a unique solution which exists for any  . The solution is denoted by
. The solution is denoted by  .
.
Driver et al. [1] have shown that if

for some matrix norm  on
on  , then every solution
, then every solution  of (1.4) tends to a finite limit at infinity which will be denoted by
of (1.4) tends to a finite limit at infinity which will be denoted by

In the paper of [2] the same statement has been proved under the condition

As we will show in Section 4.1 (see Example 4.1), conditions (1.7) and (1.9) are independent if the coefficients are time dependent. In the special case of (1.4) with constant coefficients (each  is independent of
is independent of  )
)

conditions (1.7) and (1.9) coincide and each reduces to

Moreover, considering (1.10) under the condition ( ), the existence of the finite limit of each solution (for whatever reason) implies that
), the existence of the finite limit of each solution (for whatever reason) implies that

(See [1].)
In the nonautonomous case with constant delays, it has been proved by Pituk [2] that the value of the limit can be characterized in an implicit formula by using a special solution of the adjoint equation to (1.4) and the initial values.
In this paper we prove similar results for the general delay difference system

where
(A4) is an integer, and
is an integer, and 

 .
.
The main novelty of our paper is that we prove the existence of the limit of the solutions of the above equations under much weaker conditions than (1.9). Moreover, utilizing our new limit formula, we show that some of our sufficient conditions are also necessary.
After recalling some preliminary facts on matrices in the next section, we state our main results on the asymptotic constancy of the solutions of (1.13), and derive a generalization of the limit formula (1.12) to the time-dependent case (Section 3). Section 4 is divided into three parts. In Section 4.1 we illustrate the independence of conditions (1.7) and (1.9). The relation between our new conditions is studied in Section 4.2. In the third part of Section 4 we specialize to (1.1), (1.4), and (1.10). The proofs of the main results are included in Section 5.
2. Preliminaries
If  is an integer, the space of all
is an integer, the space of all  matrices is denoted by
matrices is denoted by  , the zero matrix by
, the zero matrix by  , and the identity matrix by
, and the identity matrix by  .
.  is a lattice under the canonical ordering defined by what follows:
is a lattice under the canonical ordering defined by what follows:  means that
means that  for every
for every  ,
,  , where
, where  and
and  . Of course, the absolute value of
. Of course, the absolute value of  is given by
is given by 
 . The spectral radius of a matrix
. The spectral radius of a matrix  is denoted by
is denoted by  . It is well known that for any norm
. It is well known that for any norm  on
on  we have
we have  . We use that
. We use that  ,
,  ,
,  ,
,  , and
, and  imply that
imply that  .
.
3. The Main Results
Consider the general delay difference system (1.13) with the initial condition (1.6). This initial value problem has a unique solution which is denoted by  .
.
In our first theorem we give a new limit formula in terms of the initial values. To this end, we introduce the linear mapping  which is defined by
which is defined by

for any  .
.
Theorem 3.1.
Assume  . For an initial sequence
. For an initial sequence  , the solution
, the solution  of (1.13) and (1.6) has a finite limit if and only if
of (1.13) and (1.6) has a finite limit if and only if

is finite, and in this case

In the next theorem we prove the convergence of the solutions of (1.13) under a condition much weaker than (1.9), as it is illustrated in Section 4.3.
Theorem 3.2.
Assume  . If
. If
either

for some matrix norm  on
on  ,or
,or

is finite with  , then for every initial sequence
, then for every initial sequence  the solution
the solution  of (1.13) and (1.6) has a finite limit which obeys (3.3).
of (1.13) and (1.6) has a finite limit which obeys (3.3).
For the independence of conditions (3.4) and (3.5), see Section 4.1.
As a corollary, we get the next result.
Corollary 3.3.
Assume  , and for each
, and for each  let the limit
let the limit

be finite. Then the following are considered.
-
(a)
If for an initial sequence
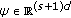 the solution
the solution  of (1.13) and (1.6) has a finite limit, then
of (1.13) and (1.6) has a finite limit, then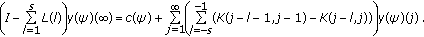 (3.7)
(3.7) -
(b)
If either
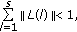 (3.8)
(3.8)
for some matrix norm  on
on  , or
, or

then for every initial sequence  the solution
the solution  of (1.13) and (1.6) has a finite limit which obeys
of (1.13) and (1.6) has a finite limit which obeys

Now consider the equation

where  for each
for each  .
.
Based on the above results we give a necessary and sufficient condition for the solutions of (3.11) to have a finite limit.
Theorem 3.4.
Consider (3.11).
-
(a)
If for every initial sequence
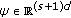 the solution
the solution  of (3.11) and (1.6) has a finite limit, then
of (3.11) and (1.6) has a finite limit, then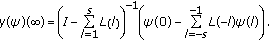 (3.12)
(3.12) -
(b)
Assume that
 for each
for each  . Then the next two statements are equivalent.
. Then the next two statements are equivalent.-
(i)
For every initial sequence
 the solution
the solution 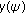 of (3.11) and (1.6) has a finite limit.
of (3.11) and (1.6) has a finite limit. -
(ii)
And
-
(i)

4. Discussion and Applications
4.1. Comparison of Conditions (1.7) and (1.9)
The independence of conditions (1.7) and (1.9) is illustrated by the next example.
Example 4.1.
Let  ,
, ,
, , and
, and  . Elementary considerations show the following.
. Elementary considerations show the following.
-
(a)
If
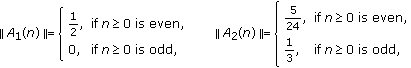 (4.1)
(4.1)then condition (1.7) is satisfied, but condition (1.9) does not hold.
-
(b)
If
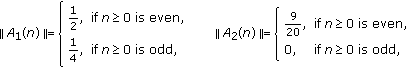 (4.2)
(4.2)
then condition (1.7) does not hold, but condition (1.9) is satisfied.
4.2. Independence of Conditions (3.4) and (3.5)
It is illustrated by the following two examples that condition (3.4) does not generally imply condition (3.5) and conversely.
Example 4.2.
Let the matrices  and
and 
 be defined by
be defined by

Since

yield that

for every matrix norm  on
on  , hence
, hence

for every matrix norm on  .
.
On the other hand

We can see that there are situations in which (3.5) is satisfied but (3.4) is not.
Example 4.3.
Let the matrices  and
and 
 be defined by
be defined by

Observe that

and therefore there exists a matrix norm  on
on  such that
such that

From

and from (4.10), it follows that there is an integer  such that
such that

This together with (4.10) gives that

Finally,

We can see that (3.4) does not imply (3.5) in general.
Suppose that 
 and the limit
and the limit

is finite for each  . In this case condition (3.4) guarantees that condition (3.5) also holds. Really,
. In this case condition (3.4) guarantees that condition (3.5) also holds. Really,

However, the implication discussed above may be lost if (4.15) is not satisfied, even if the matrices  are nonnegative, as the following example shows.
are nonnegative, as the following example shows.
Example 4.4.
Let the matrix  be defined by
be defined by

Using the  -norm
-norm  on
on  , we have
, we have

while

4.3. Application to Delay Difference Equations
For every  and
and  let the function
let the function  be defined on the set of integers by
be defined on the set of integers by

Lemma 4.5.
Assume  . Then the delay difference (1.1) is equivalent to (1.13) if for every
. Then the delay difference (1.1) is equivalent to (1.13) if for every 
 is defined by
is defined by

Proof.
It is easy to see that

By using (4.20) we get

Thus (1.1) can be written in the form

The proof is complete.
The following result is an immediate consequence of Theorem 3.2 and Lemma 4.5, and it gives sufficient conditions for the convergence of the solutions of (1.1).
Theorem 4.6.
Assume  . If either
. If either

for some matrix norm  on
on  , or
, or

is finite with  , then for every initial sequence
, then for every initial sequence  the solution
the solution  of (1.1) and (1.6) has a finite limit which obeys (3.3).
of (1.1) and (1.6) has a finite limit which obeys (3.3).
Now consider the constant delay equation (1.4). For every  , let the function
, let the function  be defined on the set of integers by
be defined on the set of integers by

In (1.4)  and
and  for every
for every  and
and  ; thus the function
; thus the function  defined in (4.20) satisfies
defined in (4.20) satisfies

for each integer  . So, in the constant delay case, from Theorem 4.6 we get the next result.
. So, in the constant delay case, from Theorem 4.6 we get the next result.
Theorem 4.7.
Assume  and
and  . If either
. If either

for some matrix norm  on
on  , or
, or

is finite with  , then for every initial sequence
, then for every initial sequence  the solution
the solution  of (1.4) and (1.6) has a finite limit which obeys (3.3).
of (1.4) and (1.6) has a finite limit which obeys (3.3).
Remark 4.8.
Our condition (4.29) is weaker than condition (1.9). In fact

Therefore

assuming that (1.9) holds.
In the next example our condition (4.29) holds, but neither condition (1.9) nor condition (1.7) can be applied.
Example 4.9.
Consider

An elementary calculation shows that

while

By applying Theorem 4.7 and Theorem 3.4(b), we give sufficient and also necessary conditions for the solutions of (1.4) to be asymptotically constant, if in addition each matrix  is constant (independent of
is constant (independent of  ).
).
Theorem 4.10.
Assume  and
and  with
with  for each
for each  and
and  . Then the following are considered.
. Then the following are considered.
-
(a)
If either
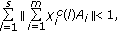 (4.36)
(4.36)for some matrix norm
 on
on 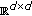 , or
, or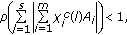 (4.37)
(4.37)then for every initial sequence
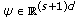 the solution
the solution of (1.10) and (1.6) has a finite limit.
of (1.10) and (1.6) has a finite limit. -
(b)
Assume that
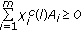 (4.38)
(4.38)
for each  . Then the next two statements are equivalent.
. Then the next two statements are equivalent.

Remark 4.11.
Condition (4.38) does not require the positivity of the coefficient matrices 
 . To illustrate this, see the following example. To the best of our knowledge, no similar result has been proved for (1.10) with both positive and negative coefficients.
. To illustrate this, see the following example. To the best of our knowledge, no similar result has been proved for (1.10) with both positive and negative coefficients.
Example 4.12.
Consider the scalar difference equation

which is a special case of (1.10). Then

Consequently, the conditions in (4.38) have the form

showing clearly that  may be negative.
may be negative.
Remark 4.13.
Of course, we have from Theorem 3.4(a) (using that  ,
, ) that if for every initial sequence
) that if for every initial sequence  the solution
the solution  of (1.10) and (1.6) has a finite limit, then (1.12) holds.
of (1.10) and (1.6) has a finite limit, then (1.12) holds.
5. Proofs of the Main Results
Proof of Theorem 3.1.
Since

it comes from (1.13) that

Now a simple calculation confirms that

From (5.3) the assertion and the desired relation (3.3) follow, bringing the proof to an end.
In order to prove Theorem 3.2, we need the following Lemma from [3, Corollary  (b)].
(b)].
Lemma 5.1.
Consider the initial value problem

where  is a given integer,
is a given integer, 

 , and
, and 
 . The unique solution of (5.4) is denoted by
. The unique solution of (5.4) is denoted by  . Let
. Let  be a norm on
be a norm on  . If
. If

is satisfied for some matrix norm  on
on  , then there are numbers
, then there are numbers  and
and  such that
such that

Proof of Theorem 3.2.
Fix an initial value  .
.
Since

it is enough to show that the series

is convergent.
Suppose (3.4). Let  be a norm on
be a norm on  . According to Lemma 5.1,
. According to Lemma 5.1,

so the series (5.8) is convergent.
Now suppose (3.5). Obviously, the convergence of the series (5.8) comes from the convergence of the series

Moreover, the members of the previous series are nonnegative, so it suffices to prove that the sequence

is bounded.
Let  be the matrix in
be the matrix in  , where
, where  for each pair
for each pair  . By the definition of the matrix
. By the definition of the matrix  , for each positive number
, for each positive number  there exists a nonnegative integer
there exists a nonnegative integer  such that
such that

The property  insures that we can choose a positive number
insures that we can choose a positive number  such that
such that  . We set
. We set

Equation (1.13) implies that

Introducing the notation

and using (5.12) and (5.13), we calculate

Hence

Because the matrix  was chosen to satisfy
was chosen to satisfy  and
and  is nonnegative,
is nonnegative,  is invertible and
is invertible and  is nonnegative too. Therefore, (5.16) yields that
is nonnegative too. Therefore, (5.16) yields that

and this gives the boundedness of the sequence (5.11).
The proof is complete.
Proof of Corollary 3.3.
-
(a)
By (3.6),
 (5.19)
(5.19)
From (3.6) it also follows that

Equations (5.19) and (5.20) together with Theorem 3.1 give the result.
-
(b)
Since conditions (3.8) and (3.9) imply that the matrix
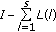 (5.21)
(5.21)
is invertible, we can apply Theorem 3.2 and (3.7).
Proof of Theorem 3.4.
-
(a)
Equations (3.7) in Corollary 3.3 and (3.1) imply that
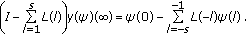 (5.22)
(5.22)
Our goal is to prove that the matrix

is invertible. To this end, we choose initial sequences  of the form
of the form  . Then (5.22) shows that the linear mapping
. Then (5.22) shows that the linear mapping

is surjective, whence it is an isomorphism. Consequently, (5.23) is invertible. Now the result follows from (5.22).
-
(b)
Suppose (i). We have proved that the matrix (5.23) is invertible. If
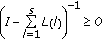 (5.25)
(5.25)
is also satisfied, then we have (ii) (see [4]). To prove this, choose initial sequences  of the form
of the form  . Then, by (5.22)
. Then, by (5.22)

Therefore, we have only to observe that  implies that
implies that  . It is enough to show that
. It is enough to show that  yields
yields

but this follows from (3.11) by an easy induction argument.
Now, suppose (ii). Then (i) comes from Corollary 3.3(b) (see the second condition).
The proof is complete.
References
Driver RD, Ladas G, Vlahos PN: Asymptotic behavior of a linear delay difference equation. Proceedings of the American Mathematical Society 1992,115(1):105-112. 10.1090/S0002-9939-1992-1111217-0
Pituk M: The limits of the solutions of a nonautonomous linear delay difference equation. Computers & Mathematics with Applications 2001,42(3–5):543-550. 10.1016/S0898-1221(01)00176-6
Győri I, Horváth L:A new view of the
 -theory of system of higher order difference equations. Computers and Mathematics with Applications 2010,59(8):2918-2932. 10.1016/j.camwa.2010.02.010
-theory of system of higher order difference equations. Computers and Mathematics with Applications 2010,59(8):2918-2932. 10.1016/j.camwa.2010.02.010Schaefer HH: Banach Lattices and Positive Operators, Die Grundlehren der Mathematischen Wissenschaften. Volume 215. Springer, New York, NY, USA; 1974:xi+376.
Acknowledgment
This paper is supported by Hungarian National Foundations for Scientific Research Grant no. K73274.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Győri, I., Horváth, L. Asymptotic Constancy in Linear Difference Equations: Limit Formulae and Sharp Conditions. Adv Differ Equ 2010, 789302 (2010). https://doi.org/10.1155/2010/789302
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/789302
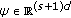 the solution
the solution  of (1.13) and (1.6) has a finite limit, then
of (1.13) and (1.6) has a finite limit, then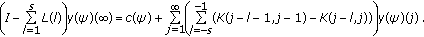
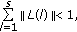
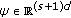 the solution
the solution  of (3.11) and (1.6) has a finite limit, then
of (3.11) and (1.6) has a finite limit, then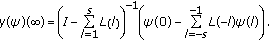
 for each
for each  . Then the next two statements are equivalent.
. Then the next two statements are equivalent. the solution
the solution 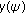 of (3.11) and (1.6) has a finite limit.
of (3.11) and (1.6) has a finite limit.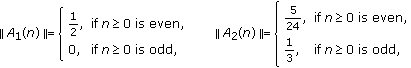
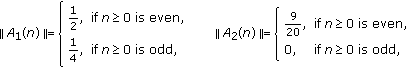
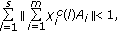
 on
on 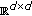 , or
, or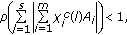
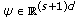 the solution
the solution of (1.10) and (1.6) has a finite limit.
of (1.10) and (1.6) has a finite limit.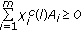

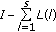
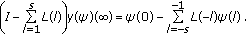
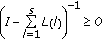
 -theory of system of higher order difference equations. Computers and Mathematics with Applications 2010,59(8):2918-2932. 10.1016/j.camwa.2010.02.010
-theory of system of higher order difference equations. Computers and Mathematics with Applications 2010,59(8):2918-2932. 10.1016/j.camwa.2010.02.010