- Research Article
- Open access
- Published:
Singular Cauchy Initial Value Problem for Certain Classes of Integro-Differential Equations
Advances in Difference Equations volume 2010, Article number: 810453 (2010)
Abstract
The existence and uniqueness of solutions and asymptotic estimate of solution formulas are studied for the following initial value problem:  ,
,  ,
,  , where
, where  is a constant and
is a constant and  . An approach which combines topological method of T. Ważewski and Schauder's fixed point theorem is used.
. An approach which combines topological method of T. Ważewski and Schauder's fixed point theorem is used.
1. Introduction and Preliminaries
The singular Cauchy problem for first-order differential and integro-differential equations resolved (or unresolved) with respect to the derivatives of unknowns is fairly well studied (see, e.g., [1–16]), but the asymptotic properties of the solutions of such equations are only partially understood. Although the singular Cauchy problems were widely considered by using various methods (see, e.g., [1–13, 16–18]), the method used here is based on a different approach. In particular, we use a combination of the topological method of T. Ważewski (see, e.g., [19, 20]) and Schauder's fixed point theorem [21]. Our technique leads to the existence and uniqueness of solutions with asymptotic estimates in the right neighbourhood of a singular point.
Consider the following problem:

where  Denote
Denote
 as
as  if there is valid
if there is valid 
 as
as  if there is valid
if there is valid 
The functions  will be assumed to satisfy the following.
will be assumed to satisfy the following.
-
(i)
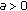 is a constant,
is a constant, 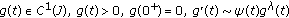 as
as 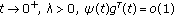 as
as 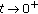 for each
for each 
-
(ii)
 as
as 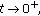 where
where  is the general solution of the equation
is the general solution of the equation  .
.
In the text we will apply the topological method of Wa ewski and Schauder's theorem. Therefore, we give a short summary of them.
ewski and Schauder's theorem. Therefore, we give a short summary of them.
Let  be a continuous function defined on an open
be a continuous function defined on an open  -set
-set  ,
,  an open set of
an open set of  the boundary of
the boundary of  with respect to
with respect to  and
and  the closure of
the closure of  with respect to
with respect to  . Consider the system of ordinary differential equations
. Consider the system of ordinary differential equations

Definition 1.1 (see [19]).
The point  is called an egress (or an ingress point) of
is called an egress (or an ingress point) of  with respect to system (1.2) if for every fixed solution of system (1.2),
with respect to system (1.2) if for every fixed solution of system (1.2),  , there exists an
, there exists an  such that
such that  for
for  . An egress point (ingress point)
. An egress point (ingress point)  of
of  is called a strict egress point (strict ingress point) of
is called a strict egress point (strict ingress point) of  if
if  on interval
on interval  for an
for an  .
.
Definition 1.2 (see [19]).
An open subset  of the set
of the set  is called a
is called a  -subset of
-subset of  with respect to system (1.2) if the following conditions are satisfied.
with respect to system (1.2) if the following conditions are satisfied.
-
(1)
There exist functions
 and
and 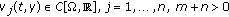 such that
such that (1.3)
(1.3) -
(2)
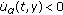 holds for the derivatives of the functions
holds for the derivatives of the functions 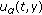 ,
,  along trajectories of system (1.2) on the set
along trajectories of system (1.2) on the set (1.4)
(1.4) -
(3)
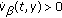 holds for the derivatives of the functions
holds for the derivatives of the functions 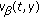 ,
, 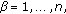 along trajectories of system (1.2) on the set
along trajectories of system (1.2) on the set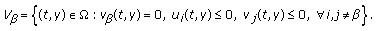 (1.5)
(1.5)
The set of all points of egress (strict egress) is denoted by  .
.
Lemma 1.3 (see [19]).
Let the set  be a
be a  -subset of the set
-subset of the set  with respect to system (1.2). Then
with respect to system (1.2). Then

Definition 1.4 (see [19]).
Let  be a topological space and
be a topological space and 
Let  . A function
. A function  such that
such that  for all
for all  is a retraction from
is a retraction from  to
to  in
in  .
.
The set  is a retract of
is a retract of  in
in  if there exists a retraction from
if there exists a retraction from  to
to  in
in  .
.
Theorem 1.5 (Ważewski's theorem [19]).
Let  be some
be some  -subset of
-subset of  with respect to system (1.2). Let
with respect to system (1.2). Let  be a nonempty compact subset of
be a nonempty compact subset of  such that the set
such that the set  is not a retract of
is not a retract of  but is a retract
but is a retract  . Then there is at least one point
. Then there is at least one point  such that the graph of a solution
such that the graph of a solution  of the Cauchy problem
of the Cauchy problem  for (1.2) lies in
for (1.2) lies in  on its right-hand maximal interval of existence.
on its right-hand maximal interval of existence.
Theorem 1.6 (Schauder's theorem [21]).
Let E be a Banach space and S its nonempty convex and closed subset. If P is a continuous mapping of S into itself and PS is relatively compact then the mapping P has at least one fixed point.
2. Main Results
Theorem 2.1.
Let assumptions (i) and (ii) hold, then for each  there exists one solution
there exists one solution  of initial problem (1.1) such that
of initial problem (1.1) such that

for  where
where  is a constant, and
is a constant, and  depends on
depends on  .
.
Proof.
( ) Denote
) Denote  the Banach space of continuous functions
the Banach space of continuous functions  on the interval
on the interval  with the norm
with the norm

The subset  of Banach space
of Banach space  will be the set of all functions
will be the set of all functions  from
from  satisfying the inequality
satisfying the inequality

The set  is nonempty, convex and closed.
is nonempty, convex and closed.
( ) Now we will construct the mapping
) Now we will construct the mapping  . Let
. Let  be an arbitrary function. Substituting
be an arbitrary function. Substituting  instead of
instead of  into (1.1), we obtain the differential equation
into (1.1), we obtain the differential equation

Set


where  is a constant and new functions
is a constant and new functions  satisfy the differential equation
satisfy the differential equation

From (2.3), it follows that

Substituting (2.5), (2.6) and (2.8) into (2.4) we get

Substituting (2.9) into (2.7) we get

In view of (2.5), (2.6) it is obvious that a solution of (2.10) determines a solution of (2.4).
Now we will use Wa ewski's topological method. Consider an open set
ewski's topological method. Consider an open set  . Investigate the behaviour of integral curves of (2.10) with respect to the boundary of the set
. Investigate the behaviour of integral curves of (2.10) with respect to the boundary of the set

where

Calculating the derivative  along the trajectories of (2.10) on the set
along the trajectories of (2.10) on the set

we obtain

Since

then there exists a positive constant  such that
such that

Consequently,

From here  and by L'Hospital's rule
and by L'Hospital's rule  for
for  is an arbitrary real number. These both identities imply that the powers of
is an arbitrary real number. These both identities imply that the powers of  affect the convergence to zero of the terms in (2.14), in decisive way.
affect the convergence to zero of the terms in (2.14), in decisive way.
Using the assumptions of Theorem 2.1 and the definition of  we get that the first term
we get that the first term  in (2.14) has the form
in (2.14) has the form

and the second term

is bounded by terms with exponents which are greater than

From here, we obtain

for sufficiently small  depending on
depending on  .
.
The relation (2.21) implies that each point of the set  is a strict ingress point with respect to (2.10). Change the orientation of the axis
is a strict ingress point with respect to (2.10). Change the orientation of the axis  into opposite. Now each point of the set
into opposite. Now each point of the set  is a strict egress point with respect to the new system of coordinates. By Wa
is a strict egress point with respect to the new system of coordinates. By Wa ewski's topological method, we state that there exists at least one integral curve of (2.10) lying in
ewski's topological method, we state that there exists at least one integral curve of (2.10) lying in  for
for  . It is obvious that this assertion remains true for an arbitrary function
. It is obvious that this assertion remains true for an arbitrary function 
Now we will prove the uniqueness of a solution of (2.10). Let  be also the solution of (2.10). Putting
be also the solution of (2.10). Putting  and substituting into (2.10), we obtain
and substituting into (2.10), we obtain

Let

where

Using the same method as above, we have

for  . It is obvious that
. It is obvious that  for
for  Let
Let  be any nonzero solution of (2.14) such that
be any nonzero solution of (2.14) such that  for
for  Let
Let  be such a constant that
be such a constant that  If the curve
If the curve  lays in
lays in  for
for  , then
, then  would have to be a strict egress point of
would have to be a strict egress point of  with respect to the original system of coordinates. This contradicts the relation (2.25). Therefore, there exists only the trivial solution
with respect to the original system of coordinates. This contradicts the relation (2.25). Therefore, there exists only the trivial solution  of (2.22), so
of (2.22), so  is the unique solution of (2.10).
is the unique solution of (2.10).
From (2.5), we obtain

where  is the solution of (2.4) for
is the solution of (2.4) for  Similarly, from (2.6), (2.9) we have
Similarly, from (2.6), (2.9) we have

It is obvious (after a continuous extension of  for
for  that
that  maps
maps  into itself and
into itself and  .
.
( ) We will prove that
) We will prove that  is relatively compact and
is relatively compact and  is a continuous mapping.
is a continuous mapping.
It is easy to see, by (2.26) and (2.27), that  is the set of uniformly bounded and equicontinuous functions for
is the set of uniformly bounded and equicontinuous functions for  By Ascoli's theorem,
By Ascoli's theorem,  is relatively compact.
is relatively compact.
Let  be an arbitrary sequence functions in
be an arbitrary sequence functions in  such that
such that

The solution  of the equation
of the equation

corresponds to the function  and
and  for
for  Similarly, the solution
Similarly, the solution  of (2.10) corresponds to the function
of (2.10) corresponds to the function  . We will show that
. We will show that  uniformly on
uniformly on  , where
, where  ,
,  is a sufficiently small constant which will be specified later. Consider the region
is a sufficiently small constant which will be specified later. Consider the region

where

There exists sufficiently small constant  such that
such that  for any
for any  ,
,  . Investigate the behaviour of integral curves of (2.29) with respect to the boundary
. Investigate the behaviour of integral curves of (2.29) with respect to the boundary  Using the same method as above, we obtain for trajectory derivatives
Using the same method as above, we obtain for trajectory derivatives

for  and any
and any  . By Wa
. By Wa ewski's topological method, there exists at least one solution
ewski's topological method, there exists at least one solution  lying in
lying in 
 . Hence, it follows that
. Hence, it follows that

and  is a constant depending on
is a constant depending on  . From (2.5), we obtain
. From (2.5), we obtain

where  is a constant depending on
is a constant depending on  This estimate implies that
This estimate implies that  is continuous.
is continuous.
We have thus proved that the mapping  satisfies the assumptions of Schauder's fixed point theorem and hence there exists a function
satisfies the assumptions of Schauder's fixed point theorem and hence there exists a function  with
with  The proof of existence of a solution of (1.1) is complete.
The proof of existence of a solution of (1.1) is complete.
Now we will prove the uniqueness of a solution of (1.1). Substituting (2.5), (2.6) into (1.1), we get

Equation (2.7) may be written in the following form:

Now we know that there exists the solution  of (1.1) satisfying (2.1) such that
of (1.1) satisfying (2.1) such that

where  is the solution of (2.36).
is the solution of (2.36).
Denote  and substituting it into (2.36), we obtain
and substituting it into (2.36), we obtain

Let

where

If (2.38) had only the trivial solution lying in  then
then  would be the only solution of (2.38) and from here, by (2.36),
would be the only solution of (2.38) and from here, by (2.36),  would be the only solution of (1.1) satisfying (2.1) for
would be the only solution of (1.1) satisfying (2.1) for  .
.
We will suppose that there exists a nontrivial solution  of (2.38) lying in
of (2.38) lying in  . Substitute
. Substitute  instead of
instead of  into (2.38), we obtain the differential equation
into (2.38), we obtain the differential equation

Calculating the derivative  along the trajectories of (2.41) on the set
along the trajectories of (2.41) on the set  , we get
, we get  for
for  .
.
By the same method as in the case of the existence of a solution of (1.1), we obtain that in  there is only the trivial solution of (2.41). The proof is complete.
there is only the trivial solution of (2.41). The proof is complete.
Example 2.2.
Consider the following initial value problem:

In our case a general solution of the equation

has the form  and
and  ,
,  ,
,  ,
,  ,
,  as
as  .
.
Further

 ,
,  as
as  and
and

According to Theorem 2.1, there exists for every constant  the unique solution
the unique solution  of (2.42) such that
of (2.42) such that

for  .
.
References
Agarwal RP, O'Regan D, Zernov OE: A singular initial value problem for some functional differential equations. Journal of Applied Mathematics and Stochastic Analysis 2004, (3):261-270. 10.1155/S1048953304405012
Čečik VA: Investigation of systems of ordinary differential equations with a singularity. Trudy Moskovskogo Matematičeskogo Obščestva 1959, 8: 155-198.
Diblík I: Asymptotic behavior of solutions of a differential equation partially solved with respect to the derivative. Siberian Mathematical Journal 1982,23(5):654-662. 10.1007/BF00971283
Diblík I: On the existence of solutions of a real system of ordinary differential equations entering into a singular point. Ukrainskii Matematicheskii Zhurnal 1986,38(6):701-707.
Baštinec J, Diblík J: On existence of solutions of a singular Cauchy-Nicoletti problem for a system of integro-differential equations. Demonstratio Mathematica 1997,30(4):747-760.
Diblík I: On the existence of 0-curves of a singular system of differential equations. Mathematische Nachrichten 1985, 122: 247-258. 10.1002/mana.19851220124
Diblík J, Nowak C: A nonuniqueness criterion for a singular system of two ordinary differential equations. Nonlinear Analysis: Theory, Methods & Applications 2006,64(4):637-656. 10.1016/j.na.2005.05.042
Diblík J, Růžičková M: Existence of positive solutions of a singular initial problem for a nonlinear system of differential equations. The Rocky Mountain Journal of Mathematics 2004,34(3):923-944. 10.1216/rmjm/1181069835
Diblík J, Růžičková M: Inequalities for solutions of singular initial problems for Carathéodory systems via Ważewski's principle. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4482-4495. 10.1016/j.na.2007.11.006
Šmarda Z: On the uniqueness of solutions of the singular problem for certain class of integro-differential equations. Demonstratio Mathematica 1992,25(4):835-841.
Šmarda Z: On a singular initial value problem for a system of integro-differential equations depending on a parameter. Fasciculi Mathematici 1995, (25):123-126.
Šmarda Z: On an initial value problem for singular integro-differential equations. Demonstratio Mathematica 2002,35(4):803-811.
Šmarda Z: Implicit singular integrodifferential equations of Fredholm type. Tatra Mountains Mathematical Publications 2007, 38: 255-263.
Zernov AE, Kuzina YuV:Qualitative investigation of the singular Cauchy problem
 . Ukrainskii Matematichnii Zhurnal 2003,55(10):1419-1424.
. Ukrainskii Matematichnii Zhurnal 2003,55(10):1419-1424.Zernov AE, Kuzina YuV: Geometric analysis of a singular Cauchy problem. Nonlinear Oscillator 2004,7(1):67-80.
Zernov AE, Chaichuk OR: Asymptotic behavior of solutions of a singular Cauchy problem for a functional-differential equation. Journal of Mathematical Sciences 2009,160(1):123-127. 10.1007/s10958-009-9491-2
Feng M, Zhang X, Li X, Ge W: Necessary and sufficient conditions for the existence of positive solution for singular boundary value problems on time scales. Advances in Difference Equations 2009, 2009:-14.
Gómez González A, Otero-Espinar V: Existence and uniqueness of positive solution for singular BVPs on time scales. Advances in Difference Equations 2009, 2009:-12.
Hartman P: Ordinary Differential Equations. John Wiley & Sons, New York, NY, USA; 1964:xiv+612.
Srzednicki R: Ważewski method and Conley index. In Handbook of Differential Equations. Elsevier/North-Holland, Amsterdam, The Netherlands; 2004:591-684.
Zeidler E: Applied Functional Analysis: Applications to Mathematical Physics, Applied Mathematical Sciences. Volume 108. Springer, New York, NY, USA; 1995:xxx+479.
Acknowledgment
The author was supported by the Council of Czech Government Grants MSM 00216 30503 and MSM 00216 30529.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Šmarda, Z. Singular Cauchy Initial Value Problem for Certain Classes of Integro-Differential Equations. Adv Differ Equ 2010, 810453 (2010). https://doi.org/10.1155/2010/810453
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/810453
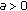 is a constant,
is a constant, 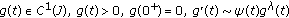 as
as 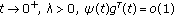 as
as 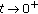 for each
for each 
 as
as 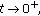 where
where  is the general solution of the equation
is the general solution of the equation  .
. and
and 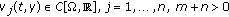 such that
such that
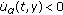 holds for the derivatives of the functions
holds for the derivatives of the functions 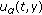 ,
,  along trajectories of system (1.2) on the set
along trajectories of system (1.2) on the set
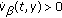 holds for the derivatives of the functions
holds for the derivatives of the functions 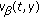 ,
, 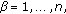 along trajectories of system (1.2) on the set
along trajectories of system (1.2) on the set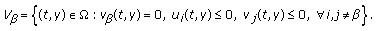
 . Ukrainskii Matematichnii Zhurnal 2003,55(10):1419-1424.
. Ukrainskii Matematichnii Zhurnal 2003,55(10):1419-1424.