- Research Article
- Open access
- Published:
Dynamical Analysis of a Delayed Predator-Prey System with Birth Pulse and Impulsive Harvesting at Different Moments
Advances in Difference Equations volume 2010, Article number: 954684 (2010)
Abstract
We consider a delayed Holling type II predator-prey system with birth pulse and impulsive harvesting on predator population at different moments. Firstly, we prove that all solutions of the investigated system are uniformly ultimately bounded. Secondly, the conditions of the globally attractive prey-extinction boundary periodic solution of the investigated system are obtained. Finally, the permanence of the investigated system is also obtained. Our results provide reliable tactic basis for the practical biological economics management.
1. Introduction
Theories of impulsive differential equations have been introduced into population dynamics lately [1, 2]. Impulsive equations are found in almost every domain of applied science and have been studied in many investigation [3–11], they generally describe phenomena which are subject to steep or instantaneous changes. In [11], Jiao et al. suggested releasing pesticides is combined with transmitting infective pests into an SI model. This may be accomplished using selecting pesticides and timing the application to avoid periods when the infective pesticides would be exposed or placing the pesticides in a location where the transmitting infective pests would not contact it. So an impulsive differential equation to model the process of releasing infective pests and spraying pesticides at different fixed moment was represented as

The biological meaning of the parameters in System (1.1) can refer to Literature [11].
Clack [12] has studied the optimal harvesting of the logistic equation, a logistic equation without exploitation as follows:

where  represents the density of the resource population at time
represents the density of the resource population at time  ,
,  is the intrinsic growth rate. the positive constant
is the intrinsic growth rate. the positive constant  is usually referred as the environmental carrying capacity or saturation level. Suppose that the population described by logistic equation (1.1) is subject to harvesting at rate
is usually referred as the environmental carrying capacity or saturation level. Suppose that the population described by logistic equation (1.1) is subject to harvesting at rate  or under the catch-per-unit effort hypothesis
or under the catch-per-unit effort hypothesis  . Then the equations of the harvested population revise, respectively, as following
. Then the equations of the harvested population revise, respectively, as following

or

where  denotes the harvesting effort.
denotes the harvesting effort.
Moreover, in most models of population dynamics, increase in population due to birth are assumed to be time dependent, but many species reproduce only during a period of the year. In between these pulses of growth, mortality takes its toll, and the population decreases. In this paper, we suggest impulsive differential equations to model the process of periodic birth pulse and impulsive harvesting. Combining (1.2) and (1.4), we can obtain a single population model with birth pulse and impulsive harvesting at different moments

where  is the density of the population.
is the density of the population.  is the death rate. The population is birth pulse as intrinsic rate of natural increase and density dependence rate of predator population are denoted by
is the death rate. The population is birth pulse as intrinsic rate of natural increase and density dependence rate of predator population are denoted by  , respectively. The pulse birth and impulsive harvesting occurs every
, respectively. The pulse birth and impulsive harvesting occurs every  period (
period ( is a positive constant).
is a positive constant).  .
.  represents the birth effort of predator population at
represents the birth effort of predator population at  ,
,  ,
,  .
.  represents the harvesting effort of predator population at
represents the harvesting effort of predator population at  ,
,  .
.
But in the natural world, there are many species (especially insects) whose individual members have a life history that takes them through two stages, immature and mature. In [13], a stage-structured model of population growth consisting of immature and mature individuals was analyzed, where the stage-structured was modeled by introduction of a constant time delay. Other models of population growth with time delays were considered in [3, 5–7, 13]. The following single- species stage-structured model was introduced by Aiello and Freedman [14] as follows:

where  represent the immature and mature populations densities, respectively,
represent the immature and mature populations densities, respectively,  represents a constant time to maturity, and
represents a constant time to maturity, and  and
and  are positive constants. This model is derived as follows. We assume that at any time
are positive constants. This model is derived as follows. We assume that at any time  , birth into the immature population is proportional to the existing mature population with proportionality constant
, birth into the immature population is proportional to the existing mature population with proportionality constant  . We then assume that the death rate of immature population is proportional to the existing immature population with proportionality constant
. We then assume that the death rate of immature population is proportional to the existing immature population with proportionality constant  . We also assume that the death rate of mature population is of a logistic nature, that is, proportional to the square of the population with proportionality constant
. We also assume that the death rate of mature population is of a logistic nature, that is, proportional to the square of the population with proportionality constant  . In this paper, we consider a delayed Holling type II predator-prey system with birth pulse and impulsive harvesting on predator population at different moments.
. In this paper, we consider a delayed Holling type II predator-prey system with birth pulse and impulsive harvesting on predator population at different moments.
The organization of this paper is as follows. In the next section, we introduce the model. In Section 3, some important lemmas are presented. In Section 4, we give the globally asymptotically stable conditions of prey-extinction periodic solution of System (2.1), and the permanent condition of System (2.1). In Section 5, a brief discussion is given in the last section to conclude this paper.
2. The Model
In this paper, we consider a delayed Holling type II predator-prey model with birth pulse and impulsive harvesting on predator population at different moments

the initial conditions for (2.1) are

where  represent the densities of the immature and mature prey populations, respectively.
represent the densities of the immature and mature prey populations, respectively.  represents the density of predator population.
represents the density of predator population.  is the intrinsic growth rate of prey population.
is the intrinsic growth rate of prey population.  represents a constant time to maturity.
represents a constant time to maturity.  is the natural death rate of the immature prey population.
is the natural death rate of the immature prey population.  is the natural death rate of the mature prey population.
is the natural death rate of the mature prey population.  is the natural death rate of the predator population. The predator population consumes prey population following a Holling type-II functional response with predation coefficients
is the natural death rate of the predator population. The predator population consumes prey population following a Holling type-II functional response with predation coefficients  , and half-saturation constant
, and half-saturation constant  .
.  is the rate of conversion of nutrients into the reproduction rate of the predators. The predator population is birth pulse as intrinsic rate of natural increase and density dependence rate of predator population are denoted by
is the rate of conversion of nutrients into the reproduction rate of the predators. The predator population is birth pulse as intrinsic rate of natural increase and density dependence rate of predator population are denoted by  , respectively. The pulse birth and impulsive harvesting occurs every
, respectively. The pulse birth and impulsive harvesting occurs every  period (
period ( is a positive constant).
is a positive constant).  .
.  represents the birth effort of predator population at
represents the birth effort of predator population at  ,
,  ,
,  .
.  represents the harvesting effort of predator population at
represents the harvesting effort of predator population at  ,
,  . In this paper, we always assume that
. In this paper, we always assume that  .
.
Before going into any details, we simplify model (2.1) and restrict our attention to the following model:

the initial conditions for (2.3) are

3. The Lemma
Before discussing main results, we will give some definitions, notations and lemmas. Let  ,
,  . Denote
. Denote  the map defined by the right hand of system (2.1). Let
the map defined by the right hand of system (2.1). Let  then
then  is said to belong to class
is said to belong to class  , if
, if
-
(i)
 is continuous in
is continuous in  and
and  , for each
, for each 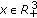 ,
, 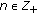 ,
,  and
and 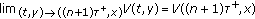 exist.
exist. -
(ii)
 is locally
is locally 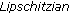 in
in  .
.
Definition 3.1.
 , then for
, then for  and
and  , the upper right derivative of
, the upper right derivative of  with respect to the impulsive differential system (2.1) is defined as
with respect to the impulsive differential system (2.1) is defined as

The solution of (2.1), denote by  , is a piecewise continuous function
, is a piecewise continuous function  :
: ,
,  is continuous on
is continuous on  and
and  ,
,  . Obviously, the global existence and uniqueness of solutions of (2.1) is guaranteed by the smoothness properties of
. Obviously, the global existence and uniqueness of solutions of (2.1) is guaranteed by the smoothness properties of  , which denotes the mapping defined by right-side of system (2.1) Lakshmikantham et al. [1]. Before we have the the main results. we need give some lemmas which will be used as follows.
, which denotes the mapping defined by right-side of system (2.1) Lakshmikantham et al. [1]. Before we have the the main results. we need give some lemmas which will be used as follows.
Now, we show that all solutions of (2.1) are uniformly ultimately bounded.
Lemma 3.2.
There exists a constant  such that
such that  ,
,  ,
,  for each solution
for each solution  of (2.1) with all
of (2.1) with all  large enough.
large enough.
Proof.
Define  .
.
(i) If
If  , then
, then  , when
, when  , we have
, we have

When 

For convenience, we make a notation as  . When
. When 

From [17, Lemma  Page
Page  ] for
] for  and
and  , we have
, we have

(ii) If  , then
, then  , we can easily obtain
, we can easily obtain

So  is uniformly ultimately bounded. Hence, by the definition of
is uniformly ultimately bounded. Hence, by the definition of  , there exists a constant
, there exists a constant  such that
such that  ,
,  for
for  large enough. The proof is complete.
large enough. The proof is complete.
If  , we have the following subsystem of System (2.1):
, we have the following subsystem of System (2.1):

We can easily obtain the analytic solution of System (3.7) between pulses, that is,

Considering the last two equations of system (3.7), we have the stroboscopic map of System (3.7) as follows:

The are two fixed points of (3.9) are obtained as  and
and  , where
, where

Lemma 3.3.
-
(i)
If
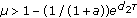 , the fixed point
, the fixed point  is globally asymptotically stable;
is globally asymptotically stable; -
(ii)
if
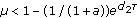 , the fixed point
, the fixed point  is globally asymptotically stable.
is globally asymptotically stable.
Proof.
For convenience, make notation  , then Difference equation (3.9) can be rewritten as
, then Difference equation (3.9) can be rewritten as

-
(i)
If
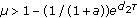 ,
,  is the unique fixed point, we have
is the unique fixed point, we have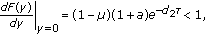 (3.12)
(3.12)then
 is globally asymptotically stable.
is globally asymptotically stable. -
(ii)
If
 ,
,  is unstable. For
is unstable. For (3.13)
(3.13)then
 is globally asymptotically stable. This complete the proof.
is globally asymptotically stable. This complete the proof.
It is well known that the following lemma can easily be proved.
Lemma 3.4.
-
(i)
If
 , the triviality periodic solution of System (3.7) is globally asymptotically stable;
, the triviality periodic solution of System (3.7) is globally asymptotically stable; -
(ii)
if
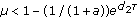 , the periodic solution of System (3.7)
, the periodic solution of System (3.7) 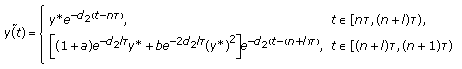 (3.14)
(3.14)
is globally asymptotically stable. Here,

Lemma 3.5 (see [ 22]).
Consider the following delay equation:

one assumes that  ;
;  for
for  . Assume that
. Assume that  . Then
. Then

4. The Dynamics
In this section, we will firstly obtain the sufficient condition of the global attractivity of prey-extinction periodic solution of System (2.1) with (2.2).
Theorem 4.1.
If


hold, the prey-extinction solution  of System (2.1) with (2.2) is globally attractive
of System (2.1) with (2.2) is globally attractive

Proof.
It is clear that the global attraction of prey-extinction periodic solution  of System (2.1) with (2.2) is equivalent to the global attraction of prey-extinction periodic solution
of System (2.1) with (2.2) is equivalent to the global attraction of prey-extinction periodic solution  of System (2.3). So we only devote to System (2.3) with (2.4). Since
of System (2.3). So we only devote to System (2.3) with (2.4). Since

we can choose  sufficiently small such that
sufficiently small such that

It follows from that the second equation of System (2.3) with (2.4) that  . So we consider the following comparison impulsive differential system:
. So we consider the following comparison impulsive differential system:

In view of Condition (4.1) and Lemma 3.4, we obtain that the periodic solution of System (4.6)

is globally asymptotically stable. Here,

By the comparison theorem of impulsive equation (see [13, Theorem  ]), we have
]), we have  and
and  as
as  . Then there exists an integer
. Then there exists an integer  ,
,  such that
such that

that is

From (2.3), we get

Consider the following comparison differential system:

from (4.5), we have  . According to Lemma 3.5, we have
. According to Lemma 3.5, we have  .
.
Let  be the solution of system (2.3) with initial conditions (2.4) and
be the solution of system (2.3) with initial conditions (2.4) and  ,
,  is the solution of system (4.12) with initial conditions
is the solution of system (4.12) with initial conditions  . By the comparison theorem, we have
. By the comparison theorem, we have  . Incorporating into the positivity of
. Incorporating into the positivity of  , we know that
, we know that

Therefore, for any  (sufficiently small), there exists an integer
(sufficiently small), there exists an integer  such that
such that  for all
for all  .
.
For System (2.3), we have

then we have  and
and  ,
,  as
as  , while
, while  and
and  are the solutions of
are the solutions of

, respectively,

Here,

Therefore, for any  . there exists a integer
. there exists a integer  ,
,  such that
such that

Let  , so we have
, so we have

for  large enough, which implies
large enough, which implies  as
as  . This completes the proof.
. This completes the proof.
The next work is to investigate the permanence of the system (2.4). Before starting our theorem, we give the definition of permanence of system (2.4).
Definition 4.2.
System (2.1) is said to be permanent if there are constants  (independent of initial value) and a finite time
(independent of initial value) and a finite time  such that for all solutions
such that for all solutions  with all initial values
with all initial values  ,
,  ,
,  ,
,  ,
,  ,
,  holds for all
holds for all  . Here
. Here  may depend on the initial values
may depend on the initial values  .
.
Theorem 4.3.
If

then there is a positive constant  such that each positive solution
such that each positive solution  of (2.3) with (2.4) satisfies
of (2.3) with (2.4) satisfies

for  large enough, where
large enough, where  is determined as the following equation:
is determined as the following equation:

Proof.
The first equation of System (2.3) can be rewritten as

Let us consider any positive solution  of System (2.3). According to(4.23),
of System (2.3). According to(4.23),  is defined as
is defined as

We calculate the derivative of  along the solution of (2.3) as follows:
along the solution of (2.3) as follows:

Equation (4.25) can also be written

We claim that for any  , it is impossible that
, it is impossible that  for all
for all  . Suppose that the claim is not valid. Then there is a
. Suppose that the claim is not valid. Then there is a  such that
such that  for all
for all  . It follows from the second equation of System (2.3) that for all
. It follows from the second equation of System (2.3) that for all  ,
,

Consider the following comparison impulsive system for all 

By Lemma 3.4, we obtain

is the unique positive periodic solution of (4.28) which is globally asymptotically stable, where

By the comparison theorem for impulsive differential equation [1, 2], we know that there exists  such that the following inequality holds for
such that the following inequality holds for  :
:

Thus,

for all  . For convenience, we make notation as
. For convenience, we make notation as  . From (4.20), we can choose a
. From (4.20), we can choose a  such that have
such that have

By (4.26), we have

for all  . Set
. Set

We will show that  for all
for all  . Suppose the contrary. Then there is a
. Suppose the contrary. Then there is a  such that
such that  for
for  and
and  . Hence, the first equation of system (2.3) and (4.33) imply that
. Hence, the first equation of system (2.3) and (4.33) imply that

This is a contradiction. Thus,  for all
for all  . As a consequence, (4.26) and (4.33) lead to
. As a consequence, (4.26) and (4.33) lead to

for all  . This implies that as
. This implies that as  ,
,  . It is a contradiction to
. It is a contradiction to  . Hence, the claim is complete.
. Hence, the claim is complete.
By the claim, we are left to consider two case. First,  for all
for all  large enough. Second,
large enough. Second,  oscillates about
oscillates about  for
for  large enough.
large enough.
Define

where  . We hope to show that
. We hope to show that  for all
for all  large enough. The conclusion is evident in first case. For the second case, let
large enough. The conclusion is evident in first case. For the second case, let  and
and  satisfy
satisfy  and
and  for all
for all  where
where  is sufficiently large such that
is sufficiently large such that

 is uniformly continuous. The positive solutions of (2.3) are ultimately bounded and
is uniformly continuous. The positive solutions of (2.3) are ultimately bounded and  is not affected by impulses. Hence, there is a
is not affected by impulses. Hence, there is a  and
and  is dependent of the choice of
is dependent of the choice of  such that
such that  for
for  . If
. If  , there is nothing to prove. Let us consider the case
, there is nothing to prove. Let us consider the case  . Since
. Since  and
and  , it is clear that
, it is clear that  for
for  . Then, proceeding exactly as the proof for the above claim. We see that
. Then, proceeding exactly as the proof for the above claim. We see that  for
for  . Because the kind of interval
. Because the kind of interval  is chosen in an arbitrary way ( we only need
is chosen in an arbitrary way ( we only need  to be large). We concluded
to be large). We concluded  for all large
for all large  . In the second case. In view of our above discussion, the choice of
. In the second case. In view of our above discussion, the choice of  is independent of the positive solution, and we proved that any positive solution of (2.3) satisfies
is independent of the positive solution, and we proved that any positive solution of (2.3) satisfies  for all sufficiently large
for all sufficiently large  . This completes the proof of the theorem.
. This completes the proof of the theorem.
From Theorems 4.1 and 4.3, we can easily obtain the following theorem.
Theorem 4.4.
If

then System (2.1) with (2.2) is permanent, where  is determined as the following equation:
is determined as the following equation:

5. Discussion
In this paper, considering the fact of the biological source management, we consider a delayed Holling type II predator-prey system with birth pulse and impulsive harvesting on predator population at different moments. We prove that all solutions of System (2.1) with (2.2) are uniformly ultimately bounded. The conditions of the globally attractive prey-extinction boundary periodic solution of System (2.1) with (2.2) are obtained. The permanence of the System (2.1) with (2.2) is also obtained. The results show that the successful management of a renewable resource is based on the concept of a sustain yield, that is, an exploitation does not the threaten the long-term persistence of the species. Our results provide reliable tactic basis for the practical biological resource management.
References
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. Volume 6. World Scientific Publishing, Teaneck, NJ, USA; 1989:xii+273.
Baĭnov D, Simeonov P: Impulsive Differential Equations: Periodic Solutions and Applications, Pitman Monographs and Surveys in Pure and Applied Mathematics. Volume 66. Longman Scientific & Technical, Harlow, UK; 1993:x+228.
Jiao J, Yang X, Cai S, Chen L: Dynamical analysis of a delayed predator-prey model with impulsive diffusion between two patches. Mathematics and Computers in Simulation 2009,80(3):522-532. 10.1016/j.matcom.2009.07.008
Jiao J-J, Chen L-s, Cai S-h: Impulsive control strategy of a pest management SI model with nonlinear incidence rate. Applied Mathematical Modelling 2009,33(1):555-563. 10.1016/j.apm.2007.11.021
Jiao J, Chen L: Global attractivity of a stage-structure variable coefficients predator-prey system with time delay and impulsive perturbations on predators. International Journal of Biomathematics 2008,1(2):197-208. 10.1142/S1793524508000163
Jiao J, Pang G, Chen L, Luo G: A delayed stage-structured predator-prey model with impulsive stocking on prey and continuous harvesting on predator. Applied Mathematics and Computation 2008,195(1):316-325. 10.1016/j.amc.2007.04.098
Kuang Y: Delay Differential Equations with Applications in Population Dynamics, Mathematics in Science and Engineering. Volume 191. Academic Press, Boston, Mass, USA; 1993:xii+398.
Liu X, Chen L: Complex dynamics of Holling type II Lotka-Volterra predator-prey system with impulsive perturbations on the predator. Chaos, Solitons and Fractals 2003,16(2):311-320. 10.1016/S0960-0779(02)00408-3
Dong L, Chen L, Sun L: Optimal harvesting policy for inshore-offshore fishery model with impulsive diffusion. Acta Mathematica Scientia. Series B 2007,27(2):405-412. 10.1016/S0252-9602(07)60040-X
Meng X, Chen L:Permanence and global stability in an impulsive Lotka-Volterra
 -species competitive system with both discrete delays and continuous delays. International Journal of Biomathematics 2008,1(2):179-196. 10.1142/S1793524508000151
-species competitive system with both discrete delays and continuous delays. International Journal of Biomathematics 2008,1(2):179-196. 10.1142/S1793524508000151Jiao J, Chen L, Luo G:An appropriate pest management
 model with biological and chemical control concern. Applied Mathematics and Computation 2008,196(1):285-293. 10.1016/j.amc.2007.05.072
model with biological and chemical control concern. Applied Mathematics and Computation 2008,196(1):285-293. 10.1016/j.amc.2007.05.072Clark CW: Mathematical Bioeconomics: The Optimal Management of Renewable Resources. Wiley-Interscience, New York, NY, USA; 1976:xi+352.
Freedman HI, Gopalsamy K: Global stability in time-delayed single-species dynamics. Bulletin of Mathematical Biology 1986,48(5-6):485-492.
Aiello WG, Freedman HI: A time-delay model of single-species growth with stage structure. Mathematical Biosciences 1990,101(2):139-153. 10.1016/0025-5564(90)90019-U
Acknowledgments
This work was supported by National Natural Science Foundation of China (no. 10961008), the Nomarch Foundation of Guizhou Province (no. 2008035), the Science Technology Foundation of Guizhou Education Department (no. 2008038), and the Science Technology Foundation of Guizhou (no. 2010J2130).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiao, J., Chen, L. Dynamical Analysis of a Delayed Predator-Prey System with Birth Pulse and Impulsive Harvesting at Different Moments. Adv Differ Equ 2010, 954684 (2010). https://doi.org/10.1155/2010/954684
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/954684
 is continuous in
is continuous in  and
and  , for each
, for each 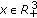 ,
, 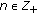 ,
,  and
and 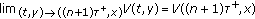 exist.
exist. is locally
is locally 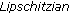 in
in  .
.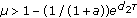 , the fixed point
, the fixed point  is globally asymptotically stable;
is globally asymptotically stable;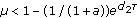 , the fixed point
, the fixed point  is globally asymptotically stable.
is globally asymptotically stable.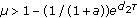 ,
,  is the unique fixed point, we have
is the unique fixed point, we have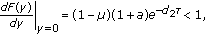
 is globally asymptotically stable.
is globally asymptotically stable. ,
,  is unstable. For
is unstable. For
 is globally asymptotically stable. This complete the proof.
is globally asymptotically stable. This complete the proof. , the triviality periodic solution of System (3.7) is globally asymptotically stable;
, the triviality periodic solution of System (3.7) is globally asymptotically stable;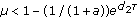 , the periodic solution of System (3.7)
, the periodic solution of System (3.7) 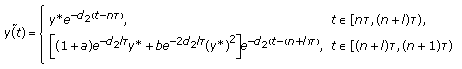
 -species competitive system with both discrete delays and continuous delays. International Journal of Biomathematics 2008,1(2):179-196. 10.1142/S1793524508000151
-species competitive system with both discrete delays and continuous delays. International Journal of Biomathematics 2008,1(2):179-196. 10.1142/S1793524508000151 model with biological and chemical control concern. Applied Mathematics and Computation 2008,196(1):285-293. 10.1016/j.amc.2007.05.072
model with biological and chemical control concern. Applied Mathematics and Computation 2008,196(1):285-293. 10.1016/j.amc.2007.05.072